Равномерное и равноускоренное движение тела по окружности доклад

Обновлено: 04.05.2024

ГОСТ

Движение, при котором за одинаковые интервалы времени тело проходит неравное расстояние, называют неравномерным (или переменным).

При переменном движении скорость тела с течением времени меняется, по этой причине для характеристики подобного перемещения применяются определения средней и моментальной скоростей.

Средней скоростью переменного движения $v_$ называют векторную величину, равную отношению перемещения тела $s$ к промежутку времени $t$, в течении которого оно совершило перемещение:

Переменное перемещение внедряет в процесс только лишь тот интервал времени, для которого эта скорость установлена. Мгновенной скоростью является скорость, какой тело обладает в определенный период времени (и значит, в конкретной точке траектории). Мгновенная скорость $v$ является пределом, к которому устремляется средняя скорость точки $v_$, в то время как промежуток времени движения точки стремится к 0:

Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к 0 (если этот порог существует), выступает главной производной этой функции по данному аргументу.

Изучим, как скатывается шарик с наклонной плоскости. Шар перемещается неровно: пути, проходимые им за последовательные одинаковые интервалы периода, увеличиваются. Таким образом, темп передвижения шарика возрастает. Перемещение объекта, скатывающегося с косой плоскости, считается классическим примером прямолинейного равноускоренного перемещения.

Рассмотрим определение равноускоренного движения.

Прямолинейным равноускоренным движением именуют прямолинейное перемещение, при котором скорость тела за любые одинаковые интервалы времени меняется на одну и ту же величину.

Прямо равноускорено способен передвигаться, к примеру, транспорт в период разгона. Но необычным может представиться в таком случае, то что во время торможения машина также способна передвигаться прямолинейно равноускорено! Так как в определении равноускоренного перемещения речь никак не идет не о росте стремительности, а только лишь об изменении скорости.

Готовые работы на аналогичную тему

Суть в том, что представление ускорения в физике обширнее, нежели в обыденном понимании. В повседневной речи под ускорением подразумевают как правило только лишь повышение быстроты. Мы в физике станем говорить, то что тело перемещается с ускорением постоянно, если быстрота тела меняется любым способом (возрастает либо снижается согласно модулю, меняется согласно направленности и т.п.).

Может возникнуть вопрос: по какой причине мы уделяем внимание непосредственно прямолинейному равноускоренному перемещению? Забегая немножко вперед, скажем, что с этим перемещением мы будем часто иметь дело при рассмотрении законов механики.

Напомним, что под воздействием стабильной силы тело перемещается прямо равноускорено. (В случае если первоначальная скорость тела равна нулю либо ориентирована по линии воздействия силы.) А в многочисленных задачах из сферы механики рассматривается непосредственно такая ситуация, в которой применяются уравнения прямолинейного равноускоренного движения, формулы конечной скорости и формулы пути без времени.

Равноускоренное движение тела

Равноускоренное движение - это перемещение тела, при каком его скорость за всевозможные одинаковые интервалы времени меняется (способна расти либо снижаться) одинаково.

Равноускоренное перемещение никак не обладает равной скоростью в течении всего пути прохождения. В этом случае имеется убыстрение, что отвечает за непрерывное повышение скорости. Ускорение перемещения остается постоянным, а темп регулярно и одинаково увеличивается.

Кроме равноускоренного имеется также равнозамедленное перемещение, где модуль темп одинаково уменьшается. Таким образом, равноускоренное перемещение способно проходить в некоторых измерениях. Оно бывает:

В случае первого — перемещение осуществляется по одной оси местоположение. В случае второго могут добавляться и прочие замеры.

Ускорение тела

Применять формулы перемещений при равноускоренном движении, а также формулы ускорения без времени возможно в абсолютно различных плоскостях. К примеру, с целью расчета падения жестких тел в свободном падении, места падения. В частности, для различных точных и геометрических расчетов.

Исходя из противопоставления равномерному перемещению, неравномерное - это движение с разной скоростью согласно каждой траектории. В чем его особенность? Это неравномерное передвижение, но оно "равно ускоряется".

Ускорение мы ассоциируем с увеличением скорости. Так как она ускоряется одинаково, получается равное увеличение скорости. Как понять, скорость равно увеличивается или нет? Нам нужно засечь время, оценить скорость через одинаковый промежуток времени, используя формулы ускорения при равноускоренном движении.

Например, автомобиль начал движение, за первые 2 сек он развил скорость до 10 м/с, за последующие 2 сек 20 м/с. Еще через 2 сек он уже едет со скоростью 30 м/с. Каждые 2 секунды темп возрастает и каждый раз на 10 м/с.

Такое передвижение и является равноускоренным. Ускорением называется величина, определяющая, насколько каждый раз увеличивается скорость. Кроме этого необходимо обратить внимание на формулу скорости при равноускоренном движении.

Перемещение с убывающей скоростью - замедленное передвижение. Однако физики каждое перемещение с изменяющейся быстротой называют ускоренным перемещением. Трогается ли автомобиль с участка (темп увеличивается), либо притормаживает - скорость снижается, в каждом случае он перемещается с ускорением.

Быстроту изменения скорости характеризует ускорение. Это число, на которое меняется скорость за каждую секунду. Если ускорение точки по модулю большое, значит точка стремительно набирает скорость (при разгоне) или быстро сбрасывает ее (при торможении). Ускорение $a$ - это физическая векторная величина, которая равна отношению перемены скорости $\delta V$ к промежутку времени $\delta t$, за которое оно произошло

Равномерное движение

Механическое передвижение, при котором тело за всевозможные одинаковые интервалы времени проходит одну и ту же дистанцию является равномерным. При равномерном перемещении значение скорости точки остаётся стабильной (формула равномерного и равноускоренного движения).

$υ$– скорость равномерного движения (м/с)
$l$– пройденный телом путь (м)
$ \delta t$– интервал времени движения (с)

Равномерное перемещение присутствует, если скорость предмета остается равной в каждом интервале пройденного пути, к этом случае период прохождения различных двух одинаковых участков будет одинаково.

В случае если перемещение является не только лишь равномерным, а и прямолинейным, в таком случае путь тела одинаковый с модулем передвижения. По этой причине, воспользовавшись аналогией с предшествующей формулой равноускоренного движения, в физике определяют скорость равномерного прямолинейного перемещения:

$ \vec$ - скорость равно прямолинейного движения, м/с
$ \vec$ - перемещение тела, м
$$ - интервал времени движения, с

Скорость равномерного прямолинейного движения является вектором, так как перемещение – величина векторная. А значит, имеет не только числовое значение, но и пространственное направление.

Равноускоренное перемещение отлично от равномерного тем, что быстрота в этом перемещении регулярно и одинаково увеличивается, вплоть до конкретного предела. В равномерном же перемещении скорость не изменяется ни в коем случае, другим образом подобное перемещение никак не станет называться равномерным.

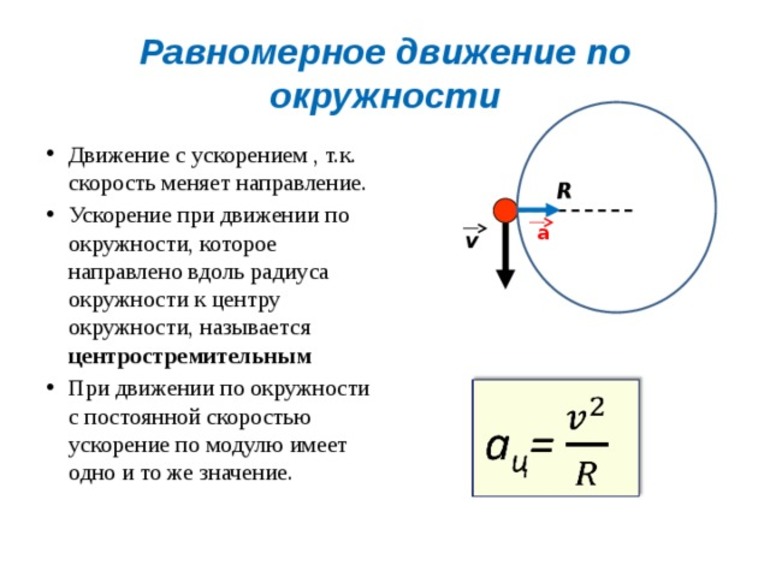
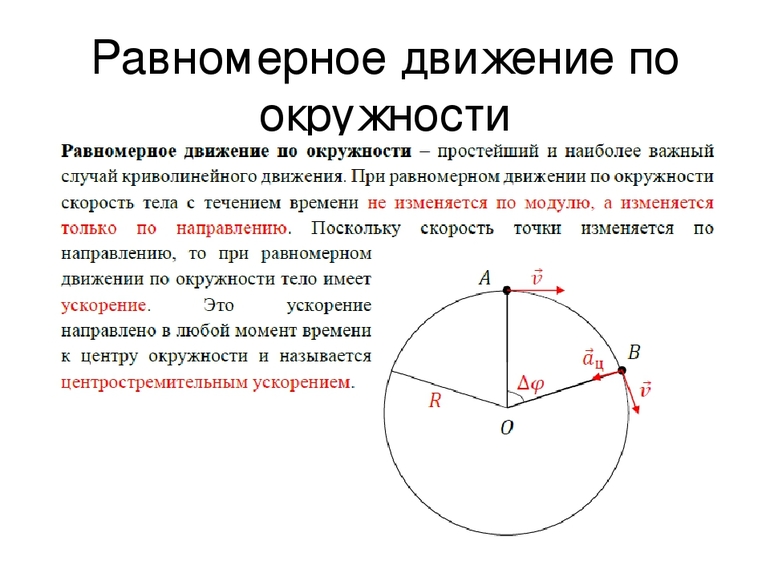
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности $ T $ — время, в течение которого тело совершает один полный оборот. Единица периода — $ [\,T\,] $ = 1 с.

Частота обращения $ (n) $ — число полных оборотов тела за одну секунду: $ n=N/t $ . Единица частоты обращения — $ [\,n\,] $ = 1 с -1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.

Связь между частотой и периодом обращения выражается формулой: $ n=1/T $ .

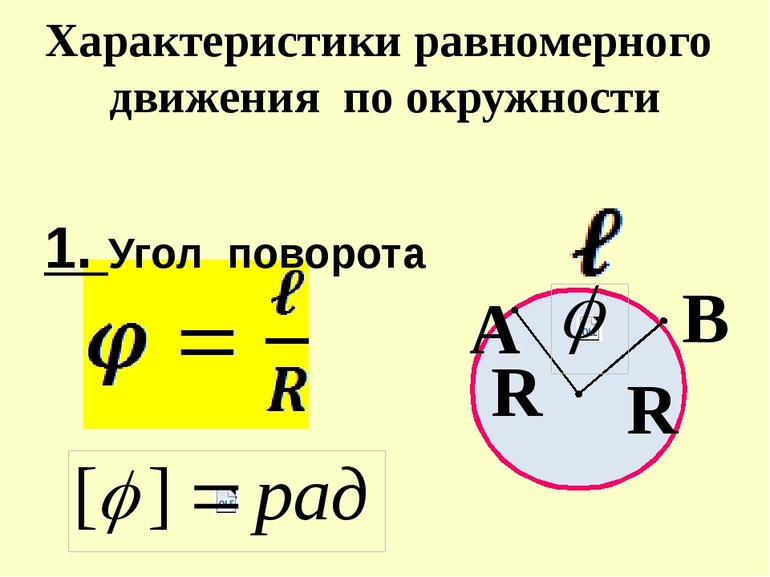
Пусть некоторое тело, движущееся по окружности, за время $ t $ переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол $ \varphi $ .

Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость $ \omega $ — физическая величина, равная отношению угла поворота $ \varphi $ радиуса-вектора к промежутку времени, за которое этот поворот произошел: $ \omega=\varphi/t $ . Единица угловой скорости — радиан в секунду, т.е. $ [\,\omega\,] $ = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен $ 2\pi $ . Поэтому $ \omega=2\pi/T $ .

Линейная скорость тела $ v $ — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: $ \vec=l/t $ . За один оборот точка проходит путь, равный длине окружности. Поэтому $ \vec=2\pi\!R/T $ . Связь между линейной и угловой скоростью выражается формулой: $ v=\omega R $ .

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: $ \vec=\frac> $ и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: $ a=\frac $ . Так как $ v=\omega R $ , то $ a=\omega^2R $ .

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии $ R_1 $ от центра вращающегося колеса, равна $ v_1 $ . Чему равна скорость $ v_2 $ точки 2, находящейся от центра на расстоянии $ R_2=4R_1 $ ?

1) $ v_2=v_1 $
2) $ v_2=2v_1 $
3) $ v_2=0,25v_1 $
4) $ v_2=4v_1 $

3. Период обращения точки по окружности можно вычислить по формуле:

1) $ T=2\pi\!Rv $
2) $ T=2\pi\!R/v $
3) $ T=2\pi v $
4) $ T=2\pi/v $

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) $ \omega=a^2R $
2) $ \omega=vR^2 $
3) $ \omega=vR $
4) $ \omega=v/R $

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

1) 200 000 с
2) 3300 с
3) 3·10 -4 с
4) 5·10 -6 с

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) $ 1/T $
2) $ v^2/R $
3) $ v/R $
4) $ \omega R $
5) $ 1/n $

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

В физике есть направление, изучающее перемещение тел относительно различных координат. Называется оно кинематикой. Один из разделов этой науки — криволинейное перемещение, частным случаем которого является равномерное движение по окружности. Описывается это понятие различными параметрами, самый важный из которых скорость. Нахождение частоты, ускорения, периода вращения довольно активно используется в авиастроении, механике и других производственных отраслях.

Общие понятия

Кинематика, входящая в состав механики, занимается изучением закономерностей движения. Под этим понятием понимается изменение положения тела относительно других объектов. Основная задача науки состоит в определении координат рассматриваемого предмета в любой момент. Кинематика изучает перемещение без учёта воздействия его вызвавшего. Любое движение считается относительным. Поэтому для его описания используют систему координат с начальной и конечной точкой отсчёта.

Для облегчения понимания процессов размерами исследуемого тела пренебрегают. Считая, что любой объект представляет собой совокупность материальных точек, повторяющих одинаковое движение при сравнении с друг другом. Существует несколько видов изменения положения. Различают их по траектории — воображаемой линии, повторяющей путь прохождения объекта. Сравнивая виды движения, выделяют два типа перемещения: прямолинейное и криволинейное.

Кроме этого, если рассматривать изменение положения во времени, движение можно различать по равномерности. При перемещении с постоянной скоростью движение называют равномерным, а при изменении её — неравномерным.

Более узкая классификация разделяет перемещение по характеру на следующие виды:

равноускоренное — это перемещение, обусловленное движением тела, при котором ускорение будет постоянным по направлению;
равнозамедленное — движение, при котором происходит отрицательное ускорение, до полного замедления объекта;
равнопеременное — при таком виде перемещения скорость изменяется на одинаковое значение в любом промежутке времени;
поступательное — если на перемещаемое тело нанести линии, они будут перемещаться параллельно сами себе;
вращательное — это периодическое движение, при котором материальная точка описывает окружность.

Частным случаем криволинейного движения, то есть по траектории, отличной от прямой линии, является равномерное движение по окружности. Определение понятия включает в себя центростремительное ускорение и постоянную по модулю скорость. Под этим видом понимают изменение положения, при котором изменяется только направление скорости.

Характеристики движения

Перемещение по окружности характеризуется постоянной по модулю скоростью: |V| = const. При этом скорость точки может изменяться по направлению. Такое её поведение называют линейным. Равномерное изменение положения по окружности является перемещением с неким ускорением. Оно всегда имеет направление к центру и считается нормальным или центростремительным. Для обозначения параметра используется символ an по вектору.

При расчёте центростремительного ускорения по модулю используется формула: an = v2 / R, где: V — линейная скорость, R — радиус, по которому вращается тело. Но так как при решении заданий удобнее пользоваться не декартовой системой координат, а учитывать ещё радиус и угол поворота, то для формулы равномерного движение по окружности вводится дополнительный параметр — угловая скорость. Обозначается она буквой ω.

С помощью неё можно узнать быстроту изменения поворота при вращении. То есть определить угол φ. Угловая скорость — скалярная величина, для её нахождения используют следующую формулу: ω = Δ φ / Δ t. В качестве единицы измерения используют радиан, делённый на секунду (рад/с).

При использовании радиусных характеристик угол поворота ко времени обратно пропорционален периоду обращения T и прямо пропорционален два пи: ω = 2p / T = 2pV. При этом учитывается и то, что угловая связана с линейной скоростью равенством: V = ω * R. Учитывая это, модуль центростремительного ускорения можно вычислить по формуле: an = ω 2 * R.

Выражение же, описывающее перемещение при прямолинейном равноускоренном изменении, выглядит как Δ s = V 0 * Δ t + (a * Δ t)/2. Таким образом, при вращении перемещение определяется углом поворота. Для поступательного же движения пройденное расстояние равняется: Δ s = (V 2 — V 0 ) / 2a, а угловое ускорение находится из выражения: Δ φ = (ω 2 — ω0) / 2a.

За направление линейной скорости принимается путь по касательной к окружности. Например, при резке металла угловой шлифовальной машинкой искры, слетающие с диска, обозначают направление скорости.

Период определяет путь, который проходит тело за определённое время. При этом пройденное расстояние равняется длине окружности. Следует отметить, что при рассмотрении скорости, изменяющейся по величине при неравномерном вращении, используют два вида ускорения: касательное и тангенциальное.

Нахождение ускорения тела

Любое криволинейное движение происходит с ускорением, так как в его ходе изменяется направление вектора скорости. Найти его — определить направление вектора и вычислить его модуль.

Окружность является самым простым видом криволинейного движения. Древние греки считали, что идеальная линия — это окружность. Можно представить, что тело движется по окружности с центром, который находится в точке O. Объект перемещается равномерно, и в какой-то момент его скорость станет V0. Вектор характеристики будет направлен по касательной и совпадать с направлением движения.

Через некоторое время тело переместится. Модуль этой скорости совпадёт с начальной. Поэтому справедливо будет записать: V0 ≠ V. Для нахождения ускорения следует решить два вопроса:

Определить направление вектора.
Найти модуль вектора ускорения.

Для ответа на первый вопрос нужно рассмотреть исходную формулу: a = ΔV / Δt. То есть найти, как изменится скорость за небольшой промежуток времени к длительности этого промежутка. Из формулы понятно, что, куда направлен вектор ΔV, в ту же сторону направлено и ускорение. Следует построить вектор изменения скорости частицы, движущейся равномерно по окружности. Для этого вектор V0 необходимо перенести параллельно самому себе в точку V.

По правилу треугольника можно построить вектор: ΔV = V — V0. Он будет направлен снизу вверх, образуя катет прямоугольного треугольника. Вектор V0 направлен по касательной к окружности, которая перпендикулярна радиусу r. Аналогичное рассуждение можно привести для вектора V0. Угол, образуемый этими отрезками в вершине O, очень мал и совпадает с углом, образованным векторами V, Vo, ΔV.

Вектор ΔV перпендикулярен вектору V, значит и вектор ускорения перпендикулярен вектору скорости. Можно утверждать, что вектор ускорения направлен к центру. Отсюда следует, что a направлен к центру окружности. Поэтому его и называют центростремительное ускорение.

Для нахождения модуля вектора используется зависимость: a = ΔV / Δt. Если известна скорость, с которой движется точка, то для нахождения её пути нужно её умножить на время (Δt). Таким образом, можно записать: ΔV / V = (V * Δt) / r. Это выражение легко упростить, умножив левую и правую часть на V / Δt. В итоге получится уравнение: V / Δt = V 2 / r. В левой части останется модуль центростремительного ускорения. Отсюда можно утверждать, что a = v 2 / r.

Решение задач

В повседневной жизни приходится постоянно встречаться с движением по окружности в динамике. Взять хотя бы оборот Земли вокруг своей оси. Кроме этого, можно привести ещё сотню примеров: вращение колёс движущего автомобиля, круговой оборот электронов вокруг атома, перемещение стрелок часов.

На уроках физики для закрепления материала часто предлагаются к самостоятельному решению несколько видов типовых задач. Вот некоторые из них:

Нужно определить центростремительное ускорение крайних точек предмета диаметром 40 см, если известно, что его угловая скорость равняется 180 рад/м. Заданные значения необходимо привести в соответствии с международной системой измерений (СИ). Вместо 40 см нужно взять 0,4 метра, а 180 рад/м — три радиана, делённые на минуту. Для решения используется определение, что ускорение равно квадрату скорости, делённому на радиус. Так как по условию дана скорость угла поворота, а не линейная, следует выразить последнюю из выражения: v = w * R. Таким образом, центростремительное ускорение для рассматриваемого случая будет равно: a = (w * R) 2 / R = w 2 * R = (w 2 * D) / 2 = (3 2 * 0.4) / 2 = 1,8 м/с 2 .
Пусть спидометр байка показывает 90 км/ч, а тахометр — 2400 оборотов в минуту. Необходимо определить радиус колеса. Вначале следует перевести данные в систему СИ. Учитывая, что в километре тысяча метров, в минуте шестьдесят секунд, а в часе 3600 секунд получается линейная скорость колеса, равная 25 метрам в секунду, и частота оборота оси 40 об/с. Тут нужно заметить, что скорость вращения колеса должна быть равна угловой скорости вращения оси: w к = w 0, так как они скреплены. Этот параметр легко может быть найден из равенства: w 0 = 2 pv 0. Радиус же находится из отношения линейной скорости, делённой на угловую скорость. Теперь останется подставить исходные данные и вычислить ответ: R = V к/ w к = v к / 2 pv = 25 / 2 pv 0 = 25 / 2 p * 40 = 0,625 = 62,5.

Это типовые задания, позволяющие понять связь между угловой и линейной скоростью, а также определять ускорение. Для того чтобы их успешно решать, нужно знать формулу углового ускорения, то есть угла поворота. А также знать, что период обращения тела, движущегося равномерно по окружности, определяют как время одного полного оборота. Обратная ему величина называется частотой. Находится она как число оборотов в единицу времени.

Занимательный пример

Пусть имеется некая планета, которая совершила полтора оборота за сорок два часа, при этом метеостанция, располагающаяся на её экваторе, прошла путь равный 50 тыс. километров, делённых на час. Нужно определить линейную и угловую скорости планеты при её вращении вокруг собственной оси. Кроме этого, вычислить, чему равны сутки, и найти радиус планеты. При этом считать, что форма космического тела — идеальный шар.

Для решения задачи следует обозначить буквой эн число оборотов: n = 1,5, а t — время, за которое планета их совершила. Путь же, который прошла станция, можно представить в виде материальной точки и принять за l = 50 000 км. Найти же будет нужно линейную и угловую скорости. Кроме этого, по условию задачи нужно найти сутки, длина которых равняется периоду — полному обороту планеты вокруг оси.

В такой задаче необязательно переводить данные в систему СИ. Можно использовать километры и часы, так как в задании не требуется дать ответ в соответствии с СИ, тем более что метры и секунды использовать неудобно.

Первое, что можно найти, это линейную скорость, равную отношению пройденного пути ко времени: v = l / t = 50000 / 42. Решив дробь, примерный результат будет равняться 1190 км /ч. Теперь можно найти скорость угла поворота. Нужно разделить угол, на который изменилось положение точки, на время. Так как один полный оборот — это 2p, то полтора оборота будут составлять 3p. Тогда искомая скорость будет равняться: w = φ / t = 3p / 42 = 0,22 рад/ч.

Сутки, то есть период обращения, будут определяться как полный период вращения, который можно разделить на число оборотов за это время. Формула для расчёта будет выглядеть следующим образом: T = t / N. Подставив значения, можно найти искомый период. Он будет составлять: T = 42 / 1,5 = 28 часов.

Движение тела по окружности является частным случаем криволинейного движения. Наряду с вектором перемещения удобно рассматривать угловое перемещение Δφ (или угол поворота), измеряемое в радианах (рис. 1.6.1). Длина дуги связана с углом поворота соотношением

При малых углах поворота Δl ≈ Δs.

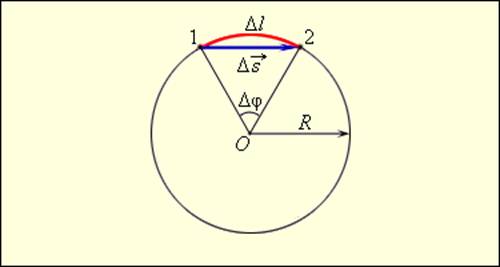
Линейное и угловое Δφ перемещения при движении тела по окружности

Угловой скоростью ω тела в данной точке круговой траектории называют предел (при Δt→0) отношения малого углового перемещения Δφ к малому промежутку времени Δt:

Угловая скорость измеряется в рад/с.

Связь между модулем линейной скорости υ и угловой скоростью ω:

При равномерном движении тела по окружности величины υ и ω остаются неизменными. В этом случае при движении изменяется только направление вектора

Равномерное движение тела по окружности является движением с ускорением. Ускорение

направлено по радиусу к центру окружности. Его называют нормальным или центростремительным ускорением. Модуль центростремительного ускорения связан с линейной υ и угловой ω скоростями соотношениями:

Для доказательства этого выражения рассмотрим изменение вектора скорости за малый промежуток времени Δt. По определению ускорения

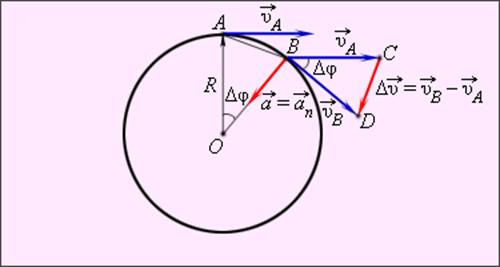
Центростремительное ускорение тела при равномерном движении по окружности

Векторы скоростей и в точках A и B направлены по касательным к окружности в этих точках. Модули скоростей одинаковы υA =υB = υ.

Из подобия треугольников OAB и BCD (рис. 1.6.2) следует:

При малых значениях угла Δφ = ωΔt расстояние |AB| =Δs ≈ υΔt. Так как |OA| = R и |CD| = Δυ, из подобия треугольников на рис. 1.6.2 получаем:

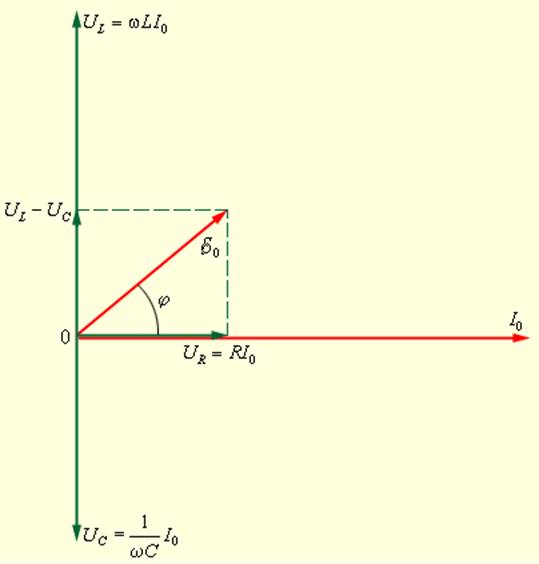
При малых углах Δφ направление вектора приближается к направлению на центр окружности. Следовательно, переходя к пределу при Δt→0, получаем:

При изменении положения тела на окружности изменяется направление на центр окружности. При равномерном движении тела по окружности модуль ускорения остается неизменным, но направление вектора ускорения изменяется со временем. Вектор ускорения в любой точке окружности направлен к ее центру. Поэтому ускорение при равномерном движении тела по окружности называется центростремительным.

В векторной форме центростремительное ускорение может быть записано в виде

где – радиус-вектор точки на окружности, начало которого находится в ее центре.

Если тело движется по окружности неравномерно, то появляется также касательная (или тангенциальная) составляющая ускорения (см 1.1):

В этой формуле Δυ_τ = υ₂ – υ₁ – изменение модуля скорости за промежуток времени Δt.

Направление вектора полного ускорения определяется в каждой точке круговой траектории величинами нормального и касательного ускорений (рис. 1.6.3).

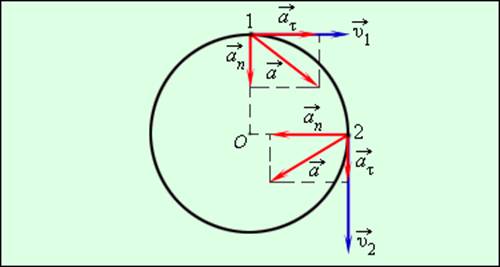
Составляющие ускорения и при неравномерном движении тела по окружности

Движение тела по окружности можно описывать с помощью двух координат x и y (плоское движение). Скорость тела в каждый момент можно разложить на две составляющие υx и υy (рис. 1.6.4).

При равномерном вращении тела величины x, y, υx, υy будут периодически изменяться во времени по гармоническому закону с периодом

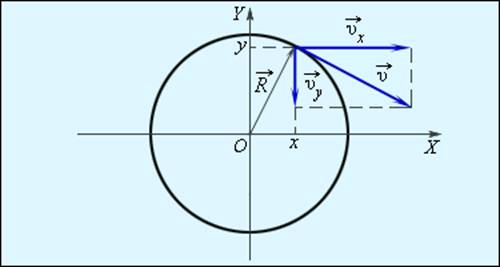
Разложение вектора скорости по координатным осям

Читайте также: