Нужно написать доклад на тему иррациональные числа
Обновлено: 18.05.2024
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Система задач на формирование понятия иррационального числа
в школьном курсе математики
Пелевина Н.Н.
Россия, г. Тольятти
В VI в. до н.э. со времен Пифагора было установлено существование несоизмеримых отрезков, или, говоря другими словами, отмечает А.В. Дорофеева [ 5, С.32], открытие иррациональности.
Только в XVII веке множество таких чисел, отмечает В.С. Малаховский [10,С.27], которые нельзя выразить отношением двух целых чисел, прочно вошло в европейскую математику как множество иррациональных чисел (от лат. irrational – безрассудный, не определяемый отношением).
В начале XVIII столетия существовало, как отмечает А.П. Юшкевич [20], три понятия иррационального числа :
иррациональное число трактовали как границу, к которой его рациональные приближения могут подойти как угодно близко;
число рассматривали как отношение одной величины к другой величине того же самого рода, взятой за единицу; когда величина несоизмерима с единицей, число называли иррациональным.
Государственный стандарт общего образования определяет минимум содержания основных образовательных программ по математике. В содержание темы “Действительные числа” в курсе общеобразовательной школы включены следующие вопросы [9], касающиеся иррациональных чисел.
5-9 классы: Понятие об иррациональном числе. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичное приближение иррациональных чисел.
10-11 классы (базовый и профильный уровни) : 1. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем . Свойства степени с действительным показателем. 2. Число е.
Иррациональное число авторы Н.Я. Виленкин [2], А.Г.Мордкович [11], Ю.М.Колягин [8], С.М. Никольский [15], М.И. Шабунин [19] определяют одинаково как бесконечную десятичную непериодическую дробь.
Иррациональность различных чисел доказывается в учебниках [11, 19] на примерах показывая, что число (), не является рациональным, других примеров доказательства иррациональности не приводится.
В задачнике А.Г. Мордковича приводятся такие задания: Докажите иррациональность числа: .
В учебнике М.И. Шабунина [19] приводится упражнение такого типа:
1. Докажите, что следующие числа являются иррациональными:
2. Докажите, что следующие числа являются иррациональными:
1) 0,121122111222…; 2) 2,12345678910112…
В учебном пособии С.М. Никольского [15] представлены задания следующего вида: Докажите, что каждое из чисел и иррациональное.
В учебнике Н.Я. Виленкина [2] представлены следующие упражнения:
Покажите, что следующие числа не являются рациональными:
1) 0,73773777377773…: 2) -6,565566556655556666… .
В учебнике Ю.М. Колягина [2] упражнения на доказательство иррациональности числа отсутствуют.
Действительные числа в учебниках [2,11,8,15,19], рассматриваются как объединение множества рациональных чисел с множеством иррациональных чисел, добавляется, что всякое действительное число можно записать в виде десятичной дроби (конечной или бесконечной).
Отличительной особенностью учебника Н.Я. Виленкина [2] является то, что он сначала вводит понятие действительного числа, а затем выделяет как частный случай иррациональное число.
Не претендуя на понятие системы задач, и взяв за основу схему системы задач на формирование понятия, предложенную Г.И. Саранцевым [16], мы разработали блок задач, реализующий содержание трех уровней, исходя при этом из следующих требований. Задачи должны быть направлены на:
Формирование предметно-значимых знаний и умений.
Усвоение содержания понятия иррационального числа.
Приобретение навыков самостоятельной работы.
Мотивация введения понятия
Задача 1 [4].
Докажите, что числа и не являются рациональными.
Решение. Предположим, что - рациональное число, представим его виде несократимой дроби , НОД, . Возведем обе части равенства в квадрат и получим: или . Это значит, что делится на нацело, то есть НОД. Следовательно, числа и не взаимно просты. А это, в свою очередь, значит, что не являются и взаимно простыми и числа . Получили противоречие. Следовательно, наше предположение неверно - рациональным числом не является.
Для числа доказательство аналогичное.
Задача 2. Какому числовому множеству принадлежит корень уравнения .
Усвоение логической структуры определения
Задача 3 [6]. Укажите какие из перечисленных чисел являются рациональными, а какие иррациональными:
а) 2,1; б); в) 0,275; г) ;
д) ; е)3,01234567891011…; ж) ; з);
Ответ: Рациональные числа: 2,1; 0,275; ;0,(2); .
Иррациональные числа: ; 3,01234567891011…;.
Задача 4 [4]. Какие из следующих корней являются рациональными, а какие - иррациональными : а) ; б) ; в) ; г) ; д) ; е) ; ж) ; з) ; и) ; к). Ответ: Рациональные: ;. Иррациональные: ;.
Задача 5 . Приведите примеры иррациональных чисел.
Задача 6 [4]. Дан прямоугольник со сторонами 2 и , в него вписаны два треугольника, как показано на рисунке.
а) Докажите, что треугольники являются равносторонними.
б) Выясните, соизмеримы ли высота вписанного треугольника и диагональ прямоугольника.
в) Выясните, каким числом (рациональным или иррациональным) выражается отношение площадей треугольника и прямоугольника.
РЕШЕНИЕ . а) Рассмотрим вписанный треугольник ABC .
АС – основание, АВ и ВС – боковые стороны, ВН – высота.
АС=, ВН=. По теореме Пифагора: АВ=
АВ=. Сторона ВС находится аналогично.
АВ=ВС=АС=, следовательно треугольник равносторонний.
б) Найдем диагональ l прямоугольника. По теореме Пифагора: . Найдем отношение высоты треугольника к диагонали прямоугольника: , следовательно высота треугольника и диагональ прямоугольника несоизмеримы.
в) Найдем площадь треугольника: . Найдем площадь прямоугольника: . Найдем отношение , следовательно отношение площадей выражается рациональным числом.
Задача 7 [17]. Докажите, что дробь 0,1234567…, в которой после запятой выписаны подряд все натуральные числа, не является периодической, т.е. не задает рациональное число.
Доказательство. Предположим, что эта дробь является периодической, тогда ее период содержит n знаков, т.е., начиная с некоторого места, будет повторяться одна и та же последовательность из n цифр. И где-то обязательно встретятся подряд n нулей, а поэтому из периодичности дроби вытекало бы, что ее период состоит из одних нулей, т.е. эта дробь является конечной. Но такой вывод противоречит способу задания дроби. Следовательно, число 0,1234567… является иррациональным.
Задача 8 [7]. Докажите, что следующие числа ,, , - иррациональные.
Решение. есть корень уравнения . Если это уравнение имеет рациональный корень, то он является целым числом и притом делителем числа 12. Совокупность делителей числа 12 состоит из следующих чисел 1,-1,2,-2,3,-3,4,-4,6,-6,12,-12. Но не одно из этих чисел не есть корень нашего уравнения. Следовательно уравнение не имеет рациональных корней и число иррационально.
Пусть . Предположим, что – рациональное число. Возведем в квадрат равенство , получим . Отсюда . Получили противоречие, так как в последнем выражении слева стоит иррациональное число, а справа – рациональное. Значит, - иррациональное число.
Задача 10 [7]. Докажите что длина диагонали квадрата, сторона которого равна 1, выражается иррациональным числом.
Задача 11 [7]. Докажите, что диагональ прямоугольника со сторонами 1 и 2 несоизмерима с его сторонами.
Задача 12 [13]. Известно, что число , входящие в формулу длины окружности и площади круга , где R – радиус окружности, является иррациональным числом. Докажите, что числа и иррациональные.
Выделение свойств множества иррациональных чисел
Задача 13 [14]. Укажите два иррациональных числа, разность которых иррациональна.
Задача 14 [12]. Может ли разность двух различных иррациональных чисел быть рациональным числом? Если не может, то почему? Если может то приведите пример.
Задача 15 [14]. Укажите два иррациональных числа, сумма которых иррациональна.
Задача 16 [17]. Приведите примеры двух положительных иррациональных чисел, таких чтобы их сумма была рациональным числом (записанных при помощи радикалов; в виде трансцендентных чисел).
Задача 17 [14]. Укажите два иррациональных числа, произведение которых иррационально.
Задача 18 [14]. Укажите два иррациональных числа, произведение которых рационально, и тем самым докажите, что множество иррациональных чисел не замкнуто относительно умножения.
Задача 19 [14]. Укажите два иррациональных числа, частное которых иррационально.
Задача 20 [14]. Укажите два иррациональных числа, частное которых рационально, и тем самым докажите, что множество иррациональных чисел не замкнуто относительно деления.
Задача 21 [18]. Докажите рациональность чисел, доказав тем самым, что множество иррациональных чисел не обладает свойством замкнутости:
Доказательство. а), следовательно, ; б) ;
в) пользуясь формулой , получим , т.е. – корень уравнения . Но так как , то уравнение имеет лишь один действительный корень и, следовательно, .
Задача 22 [17]. Выберите два произвольных рациональных числа и покажите, что между ними содержится хотя бы одно иррациональное число.
Решение. Выберем, например, числа 4,3786 и 4,32792. Первые цифры искомого числа подбираем так, чтобы , например, . Чтобы оказалось иррациональным. Можно сконструировать его в виде , где а – иррациональное число. Например, если , то .
Возьмем два рациональных числа 1 и 2, между ними содержится число -иррациональное число.
Применение понятия
Задача 23 [12]. Каким числом является сумма двух чисел, одно из которых рациональное, а другое иррациональное.
Задача 24 [17]. Могут ли быть иррациональными числа a и b , если рациональные числа a + b и ab ?
Ответ: Да, могут. Пример: , - иррациональные числа, но ,
Задача 25 [6]. Пусть – рациональное число, - иррациональное число. Рациональным или иррациональным является число:
Ответ: а) иррациональное; б) рациональное; в) иррациональное; г) рациональное.
Задача 26 [6]. Пусть является иррациональным числом. Докажите, что - также иррациональное число.
Доказательство . По условию - иррациональное число. Пусть а – рациональное число, тогда - рациональное число, - рациональное число, также рациональное число. Следовательно и число так же будет рациональным числом. Получили противоречие, откуда следует, что а - иррациональное число.
Задача 27 [3]. Покажите, что найдутся такие иррациональные числа А и В, что: А В – рациональное число; А В – натуральное число.
Решение. Возможны два случая: 1) пусть - рациональное число; тогда нам удалось найти такое число, которое удовлетворяет условию задачи;
2) пусть - иррациональное число. Примем его за А , а за В примем число . Тогда - рациональное число.
Задача 28 [6]. Докажите, что корнями уравнения являются два иррациональных числа, сумма и произведение которых не только рациональные, но даже целые.
Решение. Пусть и - корни данного уравнения. По теореме Виета: .
Решив данную систему получим: 1), .
Задача 29 [6]. Докажите, что на прямой координаты любой точки либо обе рациональные, либо обе иррациональные.
Доказательство:
Пусть - иррациональное число, а – рациональное число, тогда
- рациональное число, как частное двух рациональных чисел.
Получили противоречие. Следовательно - иррациональное число
Задача 30 [3]. Сравните числа:
а) 1,(34) и 1,34 ; б) и 3; в) и 2; г) и 4 ;
д) -54,72 и -54,679; е) 3,1415 и .
Ответ: а) 1,(34) 2; г) > 4;
Задача 31 [7]. Не используя таблицы и калькулятора, вычислите квадратные корни:;.
Задача 32 [3. Найдите для следующих чисел их целые и дробные части, а также приближения по недостатку и по избытку с точностью
до 0,01 и до 0,0001: а) π = 3,1415926… ; б) – π ;
в) 0,5189773… ; г) – 0,5189773… .
Решение . а) [3,1415926] = 3 – целая часть π, – дробная часть π.
3,1415926 ≈ 3,14… по недостатку, 3,1415926 ≈ 3,1415… по недостатку;
3,1415926 ≈ 3,15… по избытку, 3,1415926 ≈ 3,1416 по избытку.
б) – π = -3,1415926. [-3,1415926] = - 4 – целая часть, 1 – 0,1415926 = 0,8584074.
= 0,8584074 – дробная часть –π.
Задача 33 . На координатной прямой построить отрезок ОА, равный гипотенузе ОС прямоугольного треугольника ОЕС с катетами | OE | = | EC | = 1. Тогда длина этого отрезка (по теореме Пифагора) окажется равной и точке А не будет соответствовать никакое рациональное число. Постройте точки соответствующие некоторым иррациональным числам – квадратным корням из натуральных чисел, не являющихся точными квадратами (от до ).
Задача 34 . Используя теорему Пифагора построить прямоугольный треугольник с гипотенузой и .
Функции и их графики
Задача 35 [7]. Докажите, что иррациональны следующие значения функции : ;.
Задача 36 [14]. Рациональными или иррациональными являются значения функции при х =3; 8; 12.
Тригонометрические функции
Задача 37 [14]. Докажите что следующие числа иррациональны: а); б) ; в); г). Полезна теорема: если многочлен с целыми коэффициентами имеет рациональный корень ( m и n – взаимно простые целые числа), то m является делителем a k , n – делителем a 0 .
а) Воспользуемся формулой тройного угла . Получим:. Применим формулу приведения и получим: . Пусть , тогда , . Данное уравнение не имеет рациональных корней, следовательно - иррационально.
Задача 38 [14]. Какие из следующих чисел рациональны:
Задача 39 [7]. Расположите в порядке возрастания следующие значения функций: 1) , , ; 2) , , .
Показательные и логарифмические функции
Задача 40 [14]. Докажите, что следующие числа иррациональны:
Решение. б) Предположим, что , a и b положительные целые числа. Имеем:
. Возведем обе части этого равенства в степень b , получим: ,
Применим основную теорему арифметики. Эта теорема утверждает, что всякое целое число единственным образом разлагается в произведение простых чисел. Согласно этой тереме равенство не возможно.
в) Предположим, что , где m и n взаимно простые натуральные числа, тогда или , что невозможно.
Александрова, Н.В. История математических терминов, понятий, обозначений: Словарь-справочник / Н.В. Александрова. – М.: Издательство ЛКИ, 2007. – С. 69-70,217.
Виленкин, Н.Я. Алгебра и математический анализ. 10 кл.: Учеб. пособие для шк. и кл. с углубл. Изуч. математики / Н.Я. Виленкин. – М.: Мнемрзина, 2004. – 335 с.
Гельфман, Э.Г. Действительные числа. Иррациональные выражения. Учебное пособие по математике для 8 класса / Э.Г. Гельфман. – Томск: Изд-во Томского ун-та, 1998. – 256с.
Звавич, Л. И. Алгебра. Углубленное изучение. 8 кл.: задачник / Л.И. Звавич, А.Р. Рязановский. – 4-е изд., испр. – М.: Мнемозина, 2006. – 284с.
Канин, Е.С. Об углубленном изучении действительных чисел / Е.С. Канин // Математика в школе. – 1999. – № 6. – С. 74–77.
Колягин, Ю.М. Алгебра и начала математического анализа. 10 класс: учеб. для уч. общеобраз. учреждений (профильный уровень) / Ю.М. Калягин, Ю.В. Сидров, М.В. Ткачева.- М.: Мнемозина, 2009. - 366 с.
Кузнецова, Г.М. Программа для общеобразовательных школ, гимназий, лицеев. Математика 5-11 класс / Г.М. Кузнецова, Н.Г. Миндюк Н.Г. – М.: Дрофа, 2001. – 238 c .
Мордкович, А.Г. Алгебра и начала математического анализа. 10 класс. Профильный уровень./ А.Г. Мордкович, П.В. Семенов. – М.: Мнемозина, 2009. – 424с.
Мордкович, А.Г. Алгебра. 8 кл.: В двух частях. Ч. 2: Задачник для общеобразоват. учреждений / А.Г. Мордкович, Т.Н. Мишустина. – 5-е изд. испр. – М.: Мнемозина, 2003. – 339с.
Муравин, Г.К. Алгебра. 8 кл.: учеб. для общеобразоват. учреждений / Г.К. Муравин, К.С. Муравин, О.В. Муравина. – 9-е изд., стереотип. – М.: Дрофа, 2006. – 255с.
Нивен, А. Числа рациональные и иррациональные / А. Нивен. – М.: Мир, 1966. –200 с.
Никольский, С.М. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учереждений: базовый и профил. Уровни / С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2009. – 430с.
Смирнова, С.И. Какое это число? / С.И. Смирнова //Математика в школе. – 2000. – №4. – С.10-12.
Чаплынин, В.Ф. Задачи в формировании действительного числа / В.Ф. Чаплыгин // Математика в школе. – 1997. – №1. – С.26-27.
Шабунин, М.И. Алгебра. Начала математического анализа. Профильный уровень: учебник для 10 класса / М.И. Шабунин, А.А. Прокофьев. – М.: БИНОМ. Лаборатория знаний, 2007. - 424 с.
Юшкевич, А.П. История математики с древнейших времен до начала XIX столетия. Том 3 / А.П. Юшкевич. – М.: Наука, 1970, С.35.

Понятие иррациональности можно встретить в философских учениях, логических концепциях и даже в психологической типологии Карла Юнга. Но нас все-таки интересует математика: что значит иррациональное число и зачем оно нужно.
О чем эта статья:
6 класс, 8 класс
Определение иррациональных чисел
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби:
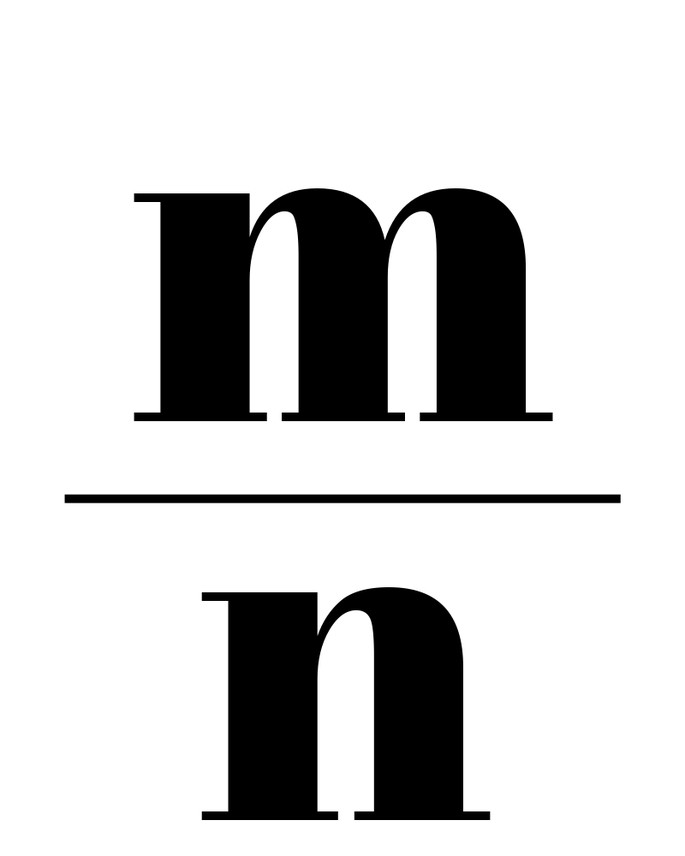
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры иррациональных чисел:
- π = 3,1415926.
- √2 = 1,41421356.
- e = 2,71828182…
- √8 = 2.828427.
- -√11= -3.31662…
Множество иррациональных чисел договорились обозначать латинской буквой I.
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Если натуральное число n не является точным квадратом, т. е. n ≠ k 2 , где k ∈ Q, то √n — иррациональное число.
Свойства иррациональных чисел
Какие числа являются иррациональными мы уже поняли, но это еще не все. Есть еще важная тема для изучения: их основные свойства.
Свойства иррациональных чисел:
- результат суммы иррационального числа и рационального равен иррациональному числу;
- результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
- результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
- результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).
Онлайн-подготовка к ОГЭ по математике — отличный способ снять стресс и закрепить знания перед экзаменом.
Определение рациональных чисел
А теперь наоборот: рассмотрим противоположное заданной теме определение.
Рациональное число — это такое число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или нуля. Если число можно получить делением двух целых чисел — это число точно рациональное.
Рациональные числа — это те, которые можно представить в виде:
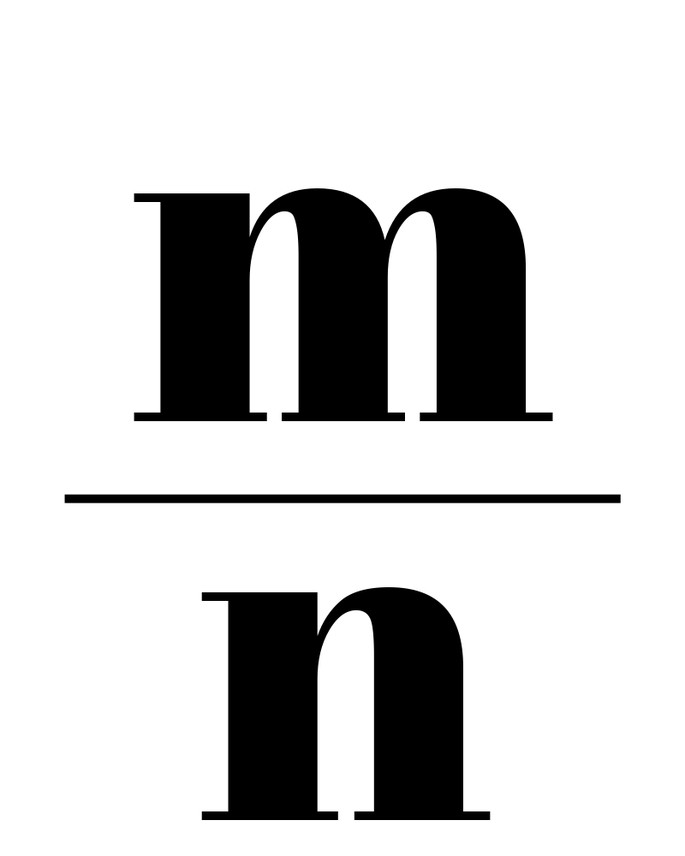
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:

- десятичная дробь 1,15 — это 115/100;
- десятичная дробь 0,2 — это 1/5;
- целое число 0 — это 0/1;
- целое число 6 — это 6/1;
- целое число 1 — это 1/1;
- бесконечная периодическая дробь 0,33333. — это 1/3;
- смешанное число это 25/10;
- отрицательная десятичная дробь -3,16 — это -316/100.
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Первое доказательство существования иррациональных чисел. Развитие теории пропорций Евдоксом Книдским. Теоремы, корень из 2 - иррациональное число. Трансцендентное число: сущность понятия, свойства, примеры, история. История уточнения числа пи.
| Рубрика | Математика |
| Вид | контрольная работа |
| Язык | русский |
| Дата добавления | 27.11.2011 |
| Размер файла | 53,9 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
1. Иррациональное числом
Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. - ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.
Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:
Отношение длины гипотенузы к длине катета равнобедренного прямоугольного треугольника может быть выражено как a:b, где a и b выбраны наименьшими из возможных.
По теореме Пифагора: a? = 2b?.
Так как a? четное, a должно быть четным (так как квадрат нечетного числа был бы нечетным).
Поскольку a:b несократима, b обязано быть нечетным.
Так как a четное, обозначим a = 2y.
Тогда a? = 4y? = 2b?.
b? = 2y?, следовательно b? четное, тогда и b четно.
Однако было доказано, что b нечетное. Противоречие.
Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты - 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе - на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.
Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.
Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 - не являющихся квадратами.
В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни - иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин: результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.
Египетский математик Абу Камил (ок. 850 г. н. э. - ок. 930 г. н.э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях - в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н.э. - 971 г. н.э.) приводит следующее определение рациональной и иррациональной величины:
Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от нее, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.
Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV-XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к р, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза.
В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667-1754) и Леонард Эйлер (1707-1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне,Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с Гейне, именно 1872 год принято считать годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.
Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века - в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.
В 1761 году Ламберт показал, что р не может быть рационально, а также что en иррационально при любом ненулевом рациональном n. Хотя доказательство Ламберта можно назвать незавершённым, принято считать его достаточно строгим, особенно учитывая время его написания. Лежандр в 1794 году, после введения функции Бесселя-Клиффорда, показал, что рІ иррационально, откуда иррациональность р следует тривиально (рациональное число в квадрате дало бы рациональное). Существование трансцендентных чисел было доказано Лиувиллемв 1844-1851 годах. Позже Георг Кантор (1873) показал их существование, используя другой метод, и обосновал, что любой интервал вещественного ряда содержит бесконечно много трансцендентных чисел. Шарль Эрмит доказал в 1873 году, что e трансцендентно, а Фердинанд Линдеман в 1882 году, основываясь на этом результате, показал трансцендентность р. Доказательство Линдеманна было затем упрощено Вейерштрассом в 1885 году, ещё более упрощено Давидом Гильбертом в 1893 году и, наконец, доведено до почти элементарного Адольфом Гурвицем и Паулем Горданом.
Всякое вещественное число может быть записано в виде бесконечной десятичной дроби, при этом иррациональные числа и только они записываются непериодическими бесконечными десятичными дробями.
Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.
Каждое трансцендентное число является иррациональным.
Каждое иррациональное число является либо алгебраическим, либо трансцендентным.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.
Множество иррациональных чисел несчётно, является множеством второй категории.
Корень из 2 - иррациональное число
Допустим противное: рационален, то есть представляется в виде несократимой дроби , где m и n - целые числа. Возведём предполагаемое равенство в квадрат:
иррациональный трансцендентный число теорема
Отсюда следует, что m2 чётно, значит, чётно и m. Пускай m = 2r, где r целое. Тогда
Следовательно, n2 чётно, значит, чётно и n. Мы получили, что m и n чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и - иррациональное число.
log 23 - иррациональное число
Допустим противное: log 23 рационален, то есть представляется в виде дроби , где m и n - целые числа. Поскольку log 23 > 0, m и n могут быть выбраны положительными. Тогда
Но 2m чётно, а 3n нечётно. Получаем противоречие.
e - иррациональное число
Другие иррациональные числа
Иррациональные числа ж(3) - v2 - v3 - v5 - ц - б - e - р - д
для любого натурального n, не являющегося точным квадратом
ex для любого рационального
ln x для любого положительного рационального
р, а также рn для любого натурального n
2. Трансцендемнтное числом
Трансцендемнтное числом (от лат. Transcendere - переходить, превосходить) - это вещественное или комплексное число, не являющееся алгебраическим - иными словами, число, которое не может быть корнем многочлена с целыми коэффициентами.
Множество трансцендентных чисел континуально.
Каждое трансцендентное вещественное число является иррациональным, но обратное неверно. Например, число - иррациональное, но не трансцендентное: оно является корнем многочлена (и потому является алгебраическим).
Основание натуральных логарифмов .
Десятичный логарифм любого целого числа, кроме чисел вида .
, и , для любого ненулевого алгебраического числа (по теореме Линдемана-Вейерштрасса).
Впервые понятие трансцендентного числа ввёл Ж. Лиувилль в 1844 году, когда доказал теорему о том, что алгебраическое число невозможно слишком хорошо приблизить рациональной дробью.
В 1873 году Ш. Эрмит доказал трансцендентность числа e (основания натуральных логарифмов).
В 1882 году Линдеман доказал теорему о трансцендентности степени числа e с ненулевым алгебраическим показателем, тем самым доказав трансцендентность числа и неразрешимость задачи квадратуры круга.
3. Число р
Число пи - одна из фундаментальных математических констант, равная отношению длины окружности к ее диаметру в пространстве с евклидовой (плоской) метрикой. Название числа происходит от греческой буквы "пи" (р), которой оно традиционно обозначается.
Число пи является иррациональным, то есть, не может быть выражено как отношение двух целых чисел и представляется бесконечной непериодической десятичной дробью. Число пи является трансцендентным, то есть, не является корнем какого-либо полинома с целыми коэффициентами.
Точное значение числа пи невозможно записать. На протяжении всей истории математики не прекращается работа по уточнению значения числа пи. О том, насколько далеко продвинулись математики, можно судить по количеству десятичных знаков числа пи, которое им удалось определить.
Четыре тысячи лет назад надежно были известны всего два первых знака числа пи. В начале XXI века с помощью многопроцессорных суперкомпьютеров определено более триллиона знаков десятичной записи сила пи. Во всей этой огромной последовательности цифр не выявлено никакой закономерности, позволяющей надежно или хотя бы вероятностно предсказывать дальнейшие знаки числа пи.
История уточнения числа пи(р)
25/8 = 3,125 - Вавилония, начало XIX в. до н. э.
Что такое иррациональные числа? Почему они так называются? Где они используются и что собой представляют? Немногие могут без раздумий ответить на эти вопросы. Но на самом деле ответы на них довольно просты, хоть нужны не всем и в очень редких ситуациях
Сущность и обозначение
Иррациональные числа представляют собой бесконечные непериодические десятичные дроби. Необходимость введения этой концепции обусловлена тем, что для решения новых возникающих задач уже было недостаточно ранее имеющихся понятий действительных или вещественных, целых, натуральных и рациональных чисел. Например, для того, чтобы вычислить, квадратом какой величины является 2, необходимо использовать непериодические бесконечные десятичные дроби. Кроме того, многие простейшие уравнения также не имеют решения без введения концепции иррационального числа.
Это множество обозначается как I. И, как уже ясно, эти значения не могут быть представлены в виде простой дроби, в числителе которой будет целое, а в знаменателе - натуральное число.

Впервые так или иначе с этим явлением столкнулись индийские математики в VII веке до нашей эры, когда было обнаружено, что квадратные корни из некоторых величин не могут быть обозначены явно. А первое доказательство существования подобных чисел приписывают пифагорейцу Гиппасу, который сделал это в процессе изучения равнобедренного прямоугольного треугольника. Серьезный вклад в изучение этого множества привнесли еще некоторые ученые, жившие до нашей эры. Введение концепции иррациональных чисел повлекло за собой пересмотр существовавшей математической системы, вот почему они так важны.
Происхождение названия
Если ratio в переводе с латыни - это "дробь", "отношение", то приставка "ир"
придает этому слову противоположное значение. Таким образом, название множества этих чисел говорит о том, что они не могут быть соотнесены с целым или дробным, имеют отдельное место. Это и вытекает из их сущности.
Место в общей классификации
Иррациональные числа наряду с рациональными относится к группе вещественных или действительных, которые в свою очередь относятся к комплексным. Подмножеств нет, однако различают алгебраическую и трансцендентную разновидность, о которых речь пойдет ниже.

Свойства
Поскольку иррациональные числа - это часть множества действительных, то к ним применимы все их свойства, которые изучаются в арифметике (их также называют основными алгебраическими законами).
a + b = b + a (коммутативность);
(a + b) + c = a + (b + c) (ассоциативность);
a + (-a) = 0 (существование противоположного числа);
ab = ba (переместительный закон);
(ab)c = a(bc) (дистрибутивность);
a(b+c) = ab + ac (распределительный закон);
a x 1/a = 1 (существование обратного числа);
Сравнение также проводится в соответствии с общими закономерностями и принципами:
Если a > b и b > c, то a > c (транзитивность соотношения) и. т. д.
Разумеется, все иррациональные числа могут быть преобразованы с помощью основных арифметических действий. Никаких особых правил при этом нет.

Кроме того, на иррациональные числа распространяется действие аксиомы Архимеда. Она гласит, что для любых двух величин a и b справедливо утверждение, что, взяв a в качестве слагаемого достаточное количество раз, можно превзойти b.
Использование
Несмотря на то что в обычной жизни не так уж часто приходится сталкиваться с ними, иррациональные числа не поддаются счету. Их огромное множество, но они практически незаметны. Нас повсюду окружают иррациональные числа. Примеры, знакомые всем, - это число пи, равное 3,1415926. или e, по сути являющееся основанием натурального логарифма, 2,718281828. В алгебре, тригонометрии и геометрии использовать их приходится постоянно. Кстати, знаменитое значение "золотого сечения", то есть отношение как большей части к меньшей, так и наоборот, также

На числовой прямой они расположены очень плотно, так что между любыми двумя величинами, отнесенными к множеству рациональных, обязательно встречается иррациональная.
До сих пор существует масса нерешенных проблем, связанных с этим множеством. Существуют такие критерии, как мера иррациональности и нормальность числа. Математики продолжают исследовать наиболее значительные примеры на предмет принадлежности их к той или иной группе. Например, считается, что е - нормальное число, т. е. вероятность появления в его записи разных цифр одинакова. Что же касается пи, то относительно его пока ведутся исследования. Мерой иррациональности же называют величину, показывающую, насколько хорошо то или иное число может быть приближено рациональными числами.
Алгебраические и трансцендентные
Как уже было упомянуто, иррациональные числа условно разделяются на алгебраические и трансцендентные. Условно, поскольку, строго говоря, эта классификация используется для деления множества C.
Под этим обозначением скрываются комплексные числа, которые включают в себя действительные или вещественные.
Итак, алгебраическим называют такое значение, которое является корнем многочлена, не равного тождественно нулю. Например, квадратный корень из 2 будет относиться к этой категории, поскольку он является решением уравнения x 2 - 2 = 0.
Все же остальные вещественные числа, не удовлетворяющие этому условию, называются трансцендентными. К этой разновидности относятся и наиболее известные и уже упомянутые примеры - число пи и основание натурального логарифма e.

Что интересно, ни одно, ни второе не были изначально выведены математиками в этом качестве, их иррациональность и трансцендентность были доказаны через много лет после их открытия. Для пи доказательство было приведено в 1882 году и упрощено в 1894, что положило конец спорам о проблеме квадратуры круга, которые длились на протяжении 2,5 тысяч лет. Оно до сих пор до конца не изучено, так что современным математикам есть над чем работать. Кстати, первое достаточно точное вычисление этого значения провел Архимед. До него все расчеты были слишком приблизительными.
Для е (числа Эйлера или Непера), доказательство его трансцендентности было найдено в 1873 году. Оно используется в решении логарифмических уравнений.
Среди других примеров - значения синуса, косинуса и тангенса для любых алгебраических ненулевых значений.
Цель работы : Узнать что такое иррациональные числа

Узнать что такое иррациональные числа
Задачи: Узнать историю возникновения иррациональных чисел
Узнать историю возникновения иррациональных чисел.
Научиться решать примеры с иррациональными числа
Гипотеза Я думаю, что иррациональные числа широко используются в окружающем нас мире, а не только на уроках математики

Я думаю, что иррациональные числа широко используются в окружающем нас мире, а не только на уроках математики
Определение Иррациональные числа – это числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби

Иррациональные числа – это числа, которые в десятичной записи представляют собой бесконечные непериодические десятичные дроби.
Бесконечные десятичные непериодические – иррациональные числа:
5,10100100010000…; 4,101100111000…
Свойства: Сумма двух положительных иррациональных чисел может быть рациональным числом

Сумма двух положительных иррациональных чисел может быть рациональным числом.
Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя различными числами имеется иррациональное число.
История О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата,…

О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа корень из 2
История Иррациональные числа были неявным образом восприняты индийскими математиками в

Иррациональные числа были неявным образом восприняты индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.
Иррациональные числа открыли в пифагорейской школе при попытке соизмерить диагональ квадрата с его стороной. Открытие сделал Гиппас из Метапонта.
История Феодор Киренский доказал иррациональность корней натуральных чисел до 17

Феодор Киренский доказал иррациональность корней натуральных чисел до 17.
Позже Евдокс Книдский развил теорию пропорций.
История Персидский математик Аль

Персидский математик Аль Махани исследовал и классифицировал квадратичные иррациональные числа и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами.
История Египетский математик Абу

Египетский математик Абу Камил был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений
Дворец числа π . Германский король

Дворец числа π.
Германский король Фридрих Второй был настолько очарован этим числом, что посвятил ему… целый дворец Кастель дель Монте, в пропорциях которого можно вычислить π. Сейчас волшебный дворец находится под охраной ЮНЕСКО.
Тату числа π π - татуировки . Если человек наносит такую татуировку , остаётся надеяться, что он точно знает, что она обозначает
π-татуировки. Если человек наносит такую татуировку, остаётся надеяться, что он точно знает, что она обозначает. К тому же значение числа π точно можно назвать в любое время дня и ночи.
Духи под названием π . Знаменитая компания

Духи под названием π.
Знаменитая компания Givenchy выпустила коллекцию духов под названием π.
Как запомнить число π Чтобы нам не ошибаться,

Как запомнить число π
Чтобы нам не ошибаться, Надо правильно прочесть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.
Надо только постараться И запомнить всё как есть: Три, четырнадцать, пятнадцать, Девяносто два и шесть.
Три, четырнадцать, пятнадцать, Девять, два, шесть, пять, три, пять. Чтоб наукой заниматься, Это каждый должен знать.
Можно просто постараться И почаще повторять: "Три, четырнадцать, пятнадцать, Девять, двадцать шесть и пять".
Знаменитое значение "золотого сечения", то есть отношение как большей части к меньшей, так и наоборот, также относится иррациональным числом
Примеры упражнений 1. Расположите в порядке возрастания числа 4,62; 3,(3); –2,75

1.Расположите в порядке возрастания числа
4,62; 3,(3); –2,75. ; –2,63. .
2. Расположите в порядке убывания числа
1,371. ; 2,065; 2,056. ; 1,(37); –0,078. .
3. Какие целые числа расположены между числами:
а) −3,168. и 2,734. ; б) −5,106. и −1,484. ;
в) −4,06 и −1,601; г) −1,29 и 0,11?
4. Найдите приближённое значение выражения a − b, где a = 59,678. и b = 43,123. округлив предварительно а и b:
а) до десятых; б) до сотых.
Вывод Все же в обычной жизни не так уж часто приходится сталкиваться с иррациональнами числами, иррациональные числа не поддаются счету

Все же в обычной жизни не так уж часто приходится сталкиваться с иррациональнами числами, иррациональные числа не поддаются счету. Их огромное множество, но они практически незаметны. Нас повсюду окружают иррациональные числа. Примеры, знакомые всем, - это число пи, равное 3,1415926. В алгебре, тригонометрии и геометрии использовать их приходится постоянно. Кстати, знаменитое значение "золотого сечения", то есть отношение как большей части к меньшей, так и наоборот, также относится к этим числам. Таким образом, моя гипотеза частично подтвердилась.
Информационные ресурсы А.Г.Мордкович

Читайте также:

