Можно ли из тетраэдра сделать куб доклад
Обновлено: 25.06.2024
Авторы работы: ученицы 10 класса Катина Илона и Дородько Ольга Руководитель: учитель математики Дородько Е. Н. Калининградская область Гурьевский муниципальный. — презентация
Авторы работы: ученицы 10 класса Катина Илона и Дородько Ольга Руководитель: учитель математики Дородько Е. Н. Калининградская область Гурьевский муниципальный район Муниципальное общеобразовательное учреждение Петровская средняя общеобразовательная школа
3 Цель исследования: Можно ли из развертки тетраэдра сделать многогранник с большим объемом? Задачи исследования: 1. Познакомиться с объектом исследования по научным источникам, Интернет-ресурсам; 2. Провести практическую часть исследования; 3. Проанализировать полученные результаты; 4. Сформулировать направления полезного использования полученных результатов.
5 Многогранник – геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер вершинами многогранника. Многогранники бывают выпуклыми и невыпуклыми. Выпуклый многогранник называется правильным, если все его грани одинаковые правильные многоугольники и все многогранные углы при вершинах равны. Существует 5 видов правильных многогранников: 1. тетраэдр, 2. куб, 3. октаэдр, 4. додекаэдр, 5. икосаэдр.
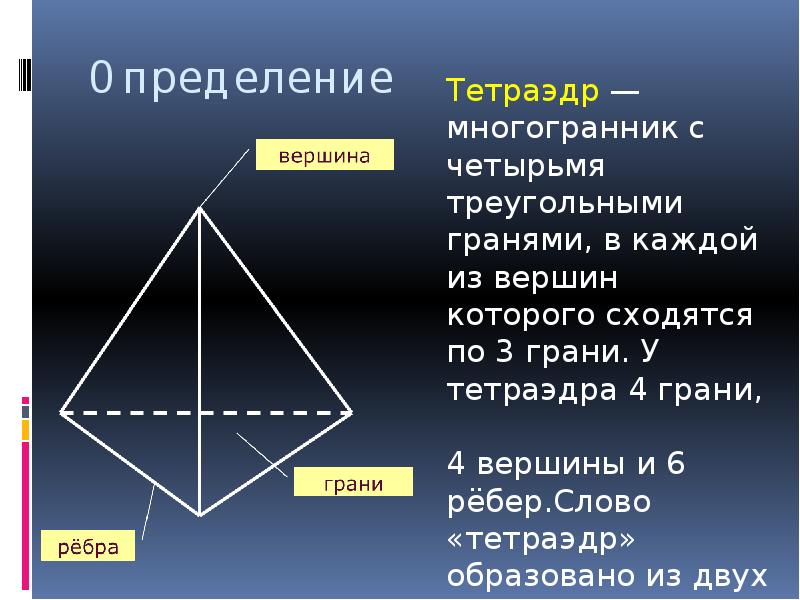
6 Тетраэдром называется треугольная пирамида, т.е. в основании пирамиды лежит треугольник. Отрезки, соединяющие вершину тетраэдра с вершинами основания, называются боковыми ребрами. Высотой называется перпендикуляр, опущенный из вершины тетраэдра на плоскость основания. Все четыре грани тетраэдра – равносторонние треугольники, шесть ребер и четыре вершины.
7 ТЕТРА-ПАКПУРЕ-ПАКТЕТРА-БРИК Производство молока и соков переживает сегодня в России настоящий бум. В этой связи стоит отметить, что большая доля произведенного объема этих продуктов упаковывается в картонную тару. По данным Tetra Pak, на этот вид тары в России приходится 85 % розлива соков.
15 Любая упаковка должна оказывать минимальное воздействие на окружающую среду; Разработка упаковки должна соответствовать требованиям уменьшения объема, повторного использования и переработки; Необходимо проводить специальную образовательную программу ознакомления всех граждан с функциями и влиянием упаковки на окружающую среду; Экологические нормативы должны применяться ко всей упаковке, включая импортную.
Увеличение объёма выпуклых многогранников
Помните, как выглядел пакет молока в советское время? Удивительно, что вся страна покупала эти пакеты почти каждый день
на протяжении более 20 лет, но мало кто сейчас помнит точно, что на них было нарисовано…
Но все конечно помнят, что пакет молока был в виде тетраэдра (правильной треугольной пирамиды).
Изобрела пакеты в виде тетраэдра фирма Тетра Пак (Tetra Pak)
в 40-х годах XX века, откуда и получила своё название. В те годы эта фирма сделала два важных нововведения.
Во-первых, жидкие продукты начали наливать в картон. Во-вторых, изготовление тетраэдральных пакетов было настолько простым,
что его можно было осуществлять прямо на молокозаводах.
Вот так выглядел наиболее распространённый пакет молока в Советском Cоюзе: красные и синие треугольники;
в форме тетраэдра (конечно, с небольшими искажениями).
Можно ли из куска картона, из которого сделан этот молочный пакет, сделать пакет с бóльшим объёмом, чем сам тетраэдр?
Математически задача формулируется так: можно ли из развёртки тетраэдра сделать многогранник с бóльшим объёмом?
А. Д. Александров 1912—1999
Александр Данилович Александров — российский математик, исследовавший обширный круг вопросов, включая геометрию выпуклых тел,
теорию меры, теорию дифференциальных уравнений в частных производных и математические основания теории относительности.
По теореме А. Д. Александрова, выпуклый многогранник с той же развёрткой, но бóльшим объёмом сделать нельзя.
Но, может быть, можно сделать невыпуклый с бóльшим объёмом?
Удивительно, но оказывается что можно!
Давайте проследим за конструкцией, предложенной Дэвидом Бликером в 1996 году. Разведём грани и на каждой добавим дополнительные
вершины и рёбра. Возьмём центральный правильный треугольник, определённый соотношением, что его сторона в два раза больше
расстояния от его вершины до стороны грани. Проведём дополнительные рёбра.
Те же построения сделаем на каждой грани. Изогнём каждую грань следующим образом: углы и середины сторон в сторону центра,
а центральный треугольничек — от центра. Все грани изогнуты одинаково, и их можно склеить в многогранник. Некоторые новые
грани лежат в одной плоскости, и рёбра между ними исчезают.
Подсчитаем объём получившегося многогранника. Для этого разобьём его на части. Полученный многогранник состоит из четырёх
одинаковых шестиугольных пирамидок и фигуры, которая является усечённым тетраэдром. Чтобы проще посчитать объём, добавим
усечённые у тетраэдра углы — маленькие тетраэдры, а от получившегося значения объёма отнимем объём добавленных кусочков.
Оказывается, что объём полученного таким способом многогранника больше чем на 37,7% превосходит объём изначального тетраэдра,
имеющего ту же развёртку! Т.е. из куска картона, из которого делались тетрадральные пакеты, можно делать пакеты,
которые вместительнее более чем на треть!
Удивительно, но тетраэдр не является исключением. Оказывается, что из развёртки любого выпуклого многогранника с треугольными
гранями можно сделать невыпуклый многогранник с бóльшим объёмом. Эту теорему доказал в 1996 году Д. Бликер и привёл
алгоритм, как это делать.
В своей статье, кроме многогранников с треугольными гранями, Д. Бликер рассмотрел два правильных многогранника, не попадающие
в этот класс — куб и додекаэдр. Из их развёрток также можно сложить невыпуклые многогранники с бóльшим объёмом,
чем у изначальных выпуклых. В 2005 году, когда создавался фильм, математики верили, что верна
Гипотеза
Из развёртки любого выпуклого многогранника всегда можно сложить невыпуклый многогранник с бóльшим объёмом.
Нерешённые задачи
Доказать (или опровергнуть) гипотезу.
Насколько большим может быть объём невыпуклого многогранника, сложенного из развёртки тетраэдра?
Другого данного выпуклого многогранника?
Летом 2006 года, двумя математиками — аспирантом МГУ Гурием Самариным и Игорем Паком из MIT — независимо
друг от друга было доказано, что гипотеза верна. Условие треугольности граней было лишь техническим моментом,
позволившем Бликеру доказать свою теорему, но в задаче оно не по существу — теорема верна и без этого условия.
Литература
Bleecker, David D. Volume increasing isometric deformations of convex polyhedra // Journal Differential Geometry. — 1996. — V. 43. — P. 505—526.
Pak I. Inflating polyhedral surfaces.
Статья. Математические этюды. 18. Увеличение объёма


Увеличение объема многогранников
Тот самый пакет молока
Помните, как выглядел пакет молока в советское время? Удивительно, что вся страна покупала эти пакеты почти каждый день на протяжении более 20 лет, но мало кто сейчас помнит точно, что на них было нарисовано…
Но все, конечно, помнят, что пакет молока был в виде тетраэдра (правильной треугольной пирамиды). Изобрела пакеты в виде тетраэдра фирма ТетраПак (TetraPak) в 40-х годах XX века, откуда и берет свое название. В те годы эта фирма сделала два важных нововведения. Во-первых, жидкие продукты начали наливать в картон. Во-вторых, изготовление тетраэдральных пакетов было настолько простым, что его можно было поместить прямо на молокозаводах.
Вот так выглядел наиболее распространенный пакет молока в Советском Союзе. Красные и синие треугольники, имел форму тетраэдра (конечно, с небольшими искажениями).
Можно ли из куска картона, из которого сделан этот молочный пакет, сделать пакет с большим объемом, чем сам тетраэдр?
Математически задача формулируется так: можно ли из развертки тетраэдра сделать многогранник с большим объемом?
По теореме А.Д. Александрова выпуклый многогранник с той же разверткой, но большим объемом сделать нельзя. Но может быть можно сделать невыпуклый с большим объемом?
Удивительно, но оказывается что можно!
Давайте проследим за конструкцией, предложенной Дэвидом Бликером в 1996 году. Разведем грани и на каждой добавим дополнительные вершины и ребра. Возьмем центральный правильный треугольник, определенный соотношением, что его сторона в два раза больше расстояния от его вершины до стороны грани. Проведем дополнительные ребра.
Те же построения сделаем на каждой грани. Изогнем каждую грань следующим образом — углы и середины сторон в сторону центра, а центральный треугольничек — от центра. Все грани изогнуты одинаково, и их можно склеить в многогранник. Некоторые новые грани лежат в одной плоскости и ребра между ними исчезают.
Подсчитаем объем получившегося многогранника. Для этого разобьем его на части. Полученный многогранник состоит из 4 одинаковых шестиугольных пирамидок и фигуры, которая является усеченным тетраэдром. Чтобы проще посчитать объем, добавим усеченные у тетраэдра углы — маленькие тетраэдры, а от получившегося значения объема отнимем объем добавленных кусочков.
Оказывается, что объем полученного таким способом многогранника больше чем на 37.7 процентов превосходит объем изначального тетраэдра, имеющего ту же развертку! Т.е. из куска картона, из которого делались тетраэдральные пакеты, можно делать пакеты которые вместительнее более чем на треть!
Удивительно, но тетраэдр не является исключением. Оказывается, что из развертки любого выпуклого многогранника с треугольными гранями можно сделать невыпуклый многогранник с бóльшим объемом. Эту теорему доказал в 1996 году Д. Бликер и привел алгоритм, как это делать.
В своей статье, кроме многогранников с треугольными гранями, Д. Бликер рассмотрел два правильных многогранника, не попадающие в этот класс — куб и додекаэдр. Из их разверток также можно сложить невыпуклые многогранники с большим объемом, чем у изначальных выпуклых.
Помните, как выглядел пакет молока в советское время? Удивительно, что вся страна покупала эти пакеты почти каждый день на протяжении более 20 лет, но мало кто сейчас помнит точно, что на них было нарисовано.
Но все конечно помнят, что пакет молока был в виде тетраэдра (правильной треугольной пирамиды). Изобрела пакеты в виде тетраэдра фирма Тетра Пак (Tetra Pak) в 40-х годах XX века, откуда и получила своё название. В те годы эта фирма сделала два важных нововведения. Во-первых, жидкие продукты начали наливать в картон. Во-вторых, изготовление тетраэдральных пакетов было настолько простым, что его можно было осуществлять прямо на молокозаводах.



Вот так выглядел наиболее распространённый пакет молока в Советском Cоюзе: красные и синие треугольники; в форме тетраэдра (конечно, с небольшими искажениями).
Можно ли из куска картона, из которого сделан этот молочный пакет, сделать пакет с бóльшим объёмом, чем сам тетраэдр?
Математически задача формулируется так: можно ли из развёртки тетраэдра сделать многогранник с бóльшим объёмом?
А. Д. Александров 1912—1999
Александр Данилович Александров — российский математик, исследовавший обширный круг вопросов, включая геометрию выпуклых тел, теорию меры, теорию дифференциальных уравнений в частных производных и математические основания теории относительности.
По теореме А. Д. Александрова, выпуклый многогранник с той же развёрткой, но бóльшим объёмом сделать нельзя. Но, может быть, можно сделать невыпуклый с бóльшим объёмом?
Удивительно, но оказывается что можно!
Давайте проследим за конструкцией, предложенной Дэвидом Бликером в 1996 году. Разведём грани и на каждой добавим дополнительные вершины и рёбра. Возьмём центральный правильный треугольник, определённый соотношением, что его сторона в два раза больше расстояния от его вершины до стороны грани. Проведём дополнительные рёбра.
Можно ли правильный тетраэдр разрезать плоскостями на части так, чтобы из них можно было сложить куб? часть плоскость куб тетраэдр
Куда ты скрылась, Русь Святая?Народ, усталый от грехов,Зовет с рыданьем Николая,Чтоб чувствовать его любовь.Наш чудотворец справедливый,Приди и в души посмотри.Ведь без тебя так сиротливо. И с каждым ты поговори.В стране, где царствует мамона,Где позабыли благодать,Где даже колоколен звонаГлухим вблизи не услыхать,Где Бога поминают всуе,Без благодарных чистых слёз,А души грешников тоскуют,Страдают, бедные, всерьез.О, Николай Святой УгодникПридет в Россию, чтоб народВ великий день его, сегодняПознал бы, для чего живет.Суровой зимнею пороюПусть чудо в нас произойдёт.И чудотворною рукоюЛюдей закроет от невзгод.У каждого души коснется,И мудрым взглядом подбодрит.И сердце радостно так бьётся!И о грехах душа скорбит.
Если два многогранника равносоставлены, то их инварианты Дена равны.
В самом деле, инвариант Дена каждого из многогранников равен сумме инвариантов его частей.
Однако инвариант Дена для куба равен нулю (так как f(\pi/2)=0), тогда как инвариант Дена для правильного тетраэдра отличен от нуля (так как f(\alpha)\ne0).
Это и завершает доказательство теоремы Дена.
Интересно, что на плоскости ничего подобного быть не может. Для плоских фигур справедлива теорема Бойяи — Гервина, которая утверждает, что два многоугольника, имеющие равные площади, равносоставлены.
Забавные сны фабрики грез Hollywood (Запад-Фильм) и Болливуд (Восток-Кино). Камо гредяши, Восток? Куда прешь, Запад? Стихия фильма состоит из слов и из образов (изображения и звуки)
Нет .Потому что при любом сечении из правильного угла основания треугольника ,составляющего 120 градусов нельзя получить угол равный 90 градусов .
Так как в каждый правильный многогранник можно вписать шар и его же вписать в шар значит -да.
Думаю,что да!Можно!Но это ответ навскидку!Хотелось бы самому это проверить в натуре.
По идее 3 взаимно перпендикулярных плоскости, имеющие общую точку в центре тетраэдра.
и как это может пригодиться? ))) Если тока хлеб в магазине попросить так разрезать))))
Скорее всего можно, одно время я увлекалась чтением литературы на эти темы
Вы можете изучить и скачать доклад-презентацию на тему Тетраэдр. Презентация на заданную тему содержит 20 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас - поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!

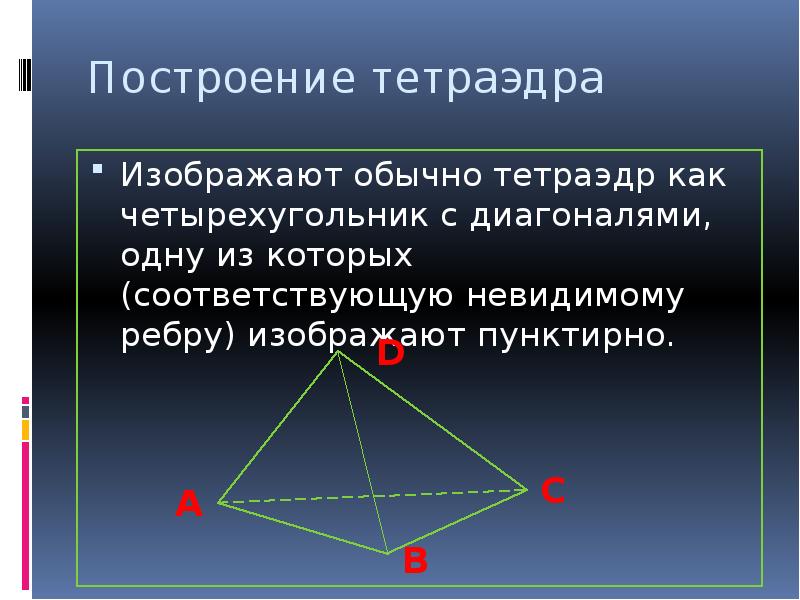















Построение тетраэдра Изображают обычно тетраэдр как четырехугольник с диагоналями, одну из которых (соответствующую невидимому ребру) изображают пунктирно.
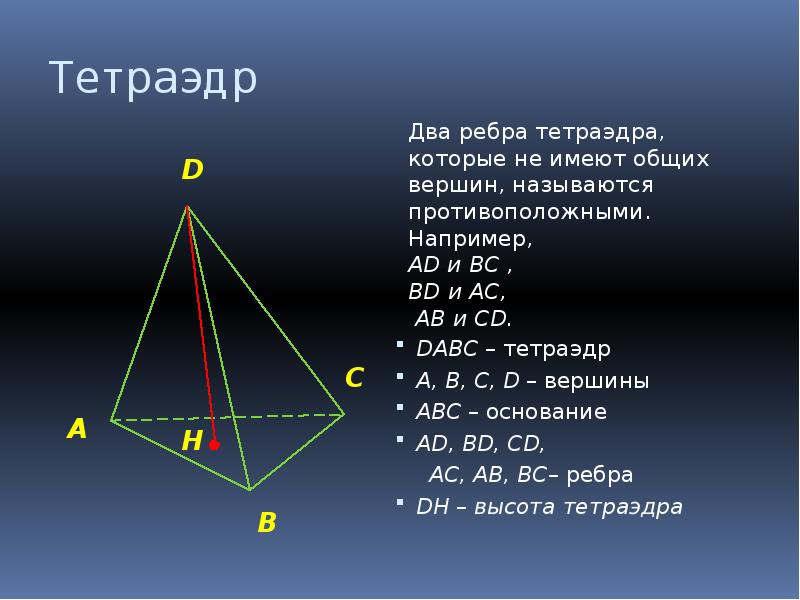
Тетраэдр DАВС – тетраэдр А, В, С, D – вершины АВС – основание АD, ВD, СD, АС, АВ, ВС– ребра DH – высота тетраэдра
Определения медианы, бимедианы(средние линии) и высоты тетраэдра Отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани, называется его медианой, опущенной из данной вершины. Отрезок, соединяющий середины скрещивающихся рёбер тетраэдра, называется его бимедианой, соединяющей данные рёбра. Отрезок, соединяющий вершину с точкой противоположной грани и перпендикулярный этой грани, называется его высотой, опущенной из данной вершины.
Высота тетраэдра Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра
Типы тетраэдров Равногранный тетраэдр – это тетраэдр, у которого все грани – равные между собой треугольники. Ортоцентрический тетраэдр – это тетраэдр, у которого все высоты, опущенные из вершин на противоположные грани, пересекаются в одной точке. Прямоугольный тетраэдр – это тетраэдр, у которого все ребра, прилежащие к одной из вершин, перпендикулярны между собой. Правильный тетраэдр – это тетраэдр, у которого все грани — равносторонние треугольники. Соразмерный тетраэдр, бивысоты которого равны. Инцентрический тетраэдр –это тетраэдр, у которого отрезки, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противоположные грани, пересекаются в одной точке.
Правильный тетраэдр Тетраэдр, все четыре грани которого — равные правильные треугольники, называется правильным тетраэдром . Правильный тетраэдр — это частный случай правильной треугольной пирамиды.
Все четыре грани правильного тетраэдра – правильные треугольники. Если длину ребра правильного тетраэдра обозначить a, то можно вычислить:
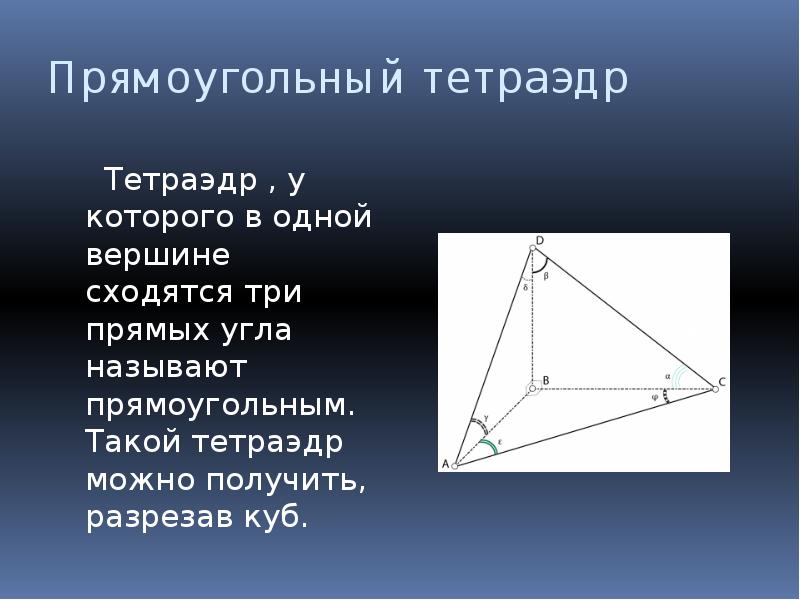
Прямоугольный тетраэдр Тетраэдр , у которого в одной вершине сходятся три прямых угла называют прямоугольным. Такой тетраэдр можно получить, разрезав куб.
Свойство тетраэдра Каждая его вершина является вершиной трех треугольников. А значит, сумма плоских углов при каждой вершине будет равна 180º. В правильный тетраэдр можно вписать октаэдр. Правильный тетраэдр можно вписать в икосаэдр, притом, четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра. Правильный тетраэдр можно вписать в куб двумя способами, притом четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба.
Тетраэдры в живой природе Некоторые плоды, находясь вчетвером на одной кисти, располагаются в вершинах тетраэдра, близкого к правильному. Такая конструкция обусловлена тем, что центры четырёх одинаковых шаров, касающихся друг друга, находятся в вершинах правильного тетраэдра. Поэтому похожие на шар плоды образуют подобное взаимное расположение. Например, таким образом могут располагаться грецкие орехи.
Тетраэдры в строительстве Тетраэдр образует жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней, часто используется в качестве основы для пространственных несущих конструкций пролётов зданий, перекрытий, балок, ферм, мостов и т. д. Стержни испытывают только продольные нагрузки.
Уголковый отражатель Уголковый отражатель — устройство в виде прямоугольного тетраэдра со взаимно перпендикулярными отражающими плоскостями. Излучение, попавшее в уголковый отражатель, отражается в строго обратном направлении. Используется:для точного измерения расстояний (для лазерной локации Луны, ИСЗ; топосъемке, строительстве); для возврата излучения точно назад (катафот, радиоэлектронная борьба).
Тетраэдры в микромире Молекула метана СН4 Молекула аммиака NH3 Алмаз C — тетраэдр с ребром равным 2,5220 ангстрем Флюорит CaF2, тетраэдр с ребром равным 3, 8626 ангстрем Сфалерит, ZnS, тетраэдр с ребром равным 3,823 ангстрем Комплексные ионы [BF4] -, [ZnCl4]2-, [Hg(CN)4]2-, [Zn(NH3)4]2+ Силикаты, в основе структур которых лежит кремнекислородный тетраэдр [SiO4]4-
Lipton tea & тетраэдр Чайная компания Lipton для разнообразия формы пакетиков для чая теперь выпускает их в виде тетраэдра
Читайте также:

