Многомерные пространства в математике доклад

Обновлено: 06.05.2024

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Актуальность исследования

Цель исследования

N -мерное пространство, многомерное пространство, проблемы многомерности пространств исследуют математики, т. к. не все уравнения и функции можно решить и исследовать на системе координат плоскости и 3-мерного пространства. Поэтому наша цель изучить многомерность пространств, сделать выводы и определить области применения методов исследования многомерных пространств.

Задачи исследования

Изучение свойств многомерных пространств.

Изучение свойств фигур этих многомерных пространств.

Представление фигур в многомерных пространствах, которые нас окружают и нет.

Определить области применения методов исследования многомерных пространств.

Объект и предмет исследования

Объект нашего исследования – представление о пространствах.

Предмет исследования – многомерные пространства и представления многомерности пространств.

Проблема исследования

Проблема исследования – исследование того, что это нельзя почувствовать и увидеть. Мы можем логически опираться на умозаключения, определения и представления многомерности пространств.

Гипотезы исследования

Представления многомерности пространств позволяют развивать методы исследования во многих областях деятельности на основе представления многомерных данных, начиная с информационных технологий, анализа больших данных на основе искусственного интеллекта.

Метод исследования

Теоретические методы исследования;

Обзор литературы и источников

По теме о многомерном пространстве проанализировано 12 200 000 сайтов в интернете на английском языке и 2 950 000 сайтов на русском языке.

В базе научных публикаций Scopus по теме о многомерном пространстве проанализировано 15 742 публикации. По типу доступа: в открытом доступе 1802 документа, 13940 другие. С 1920 г. по годам: 55 документов за 2020 г., 898 за 2019 г., 946 за 2018 г., 838 за 2017 г., 834 за 2016 г. Среди 105 авторов, наиболее публикуемых по теме (от 6 до 43 документов), больше всего документов опубликовали Melnikov , V . N . (43); Chinesta , F .(39); Ivashchuk , V . D .(35); Zhuk , A .(34); Xu , L .(28); Ammar , A .(24 документа). По отраслям знаний: по компьютерным технологиям (5 671), по математике (4 419), по проектированию (4 058), по физике (2 586), в области социальных наук (1 294 документа). По типам документов: 10 600 статей, 4 257 докладов конференций, 308 обзоров, 168 обзоров конференций. По стадиям публикации: 15 636 опубликованных статей, 106 статей в печати. Поназваниямисточников : Lecture Notes In Computer Science, включаясерии Lecture Notes In Artificial Intelligence и Lecture Notes In Bioinformatics ( 494 ) ; Proceedings Of SPIE, the International Society For Optical Engineering ( 228 ); Journal Of Chemical Physics ( 130 ); Journal Of Computational Physics ( 82 документов ).

По ключевым словам: алгоритмы (1 319); оптимизация (710), многомерное пространство (655), многомерное масштабирование (651), компьютерное моделирование (587), математические модели (539), визуализация (539), многомерные данные (505), алгоритм (439), анализ главных компонент (372), обработка сигналов (371), распознавание образов (369), контролируемое исследование (363), интеллектуальный анализ данных (352), решение задач (339), искусственный интеллект (338), визуализация данных (317), векторные пространства (317), векторы (309), системы баз данных (301), нейронные сети (297), методология (294), обработка изображений (290), кластерный анализ (278), алгоритмы кластеризации (276), Физиология(272), геометрия (266), матричная алгебра (258), структуры данных (248), принятие решений (245), численные методы (241), выделение признаков (231), классификация (информации) (230), редукция данных (227), генетические алгоритмы (222), системы обучения (219), оценка параметров (214), итерационные методы (212), семантика (212), анализ изображений (211), вычислительная сложность (207), вероятность (206), индексирование (информации) (204), классификация (203), деревья (математика) (203), топология (199), картографирование (189), многомерные системы (179), обработка данных (176), дистанционное зондирование (171), обработка запросов (170), обработка данных (167), интерполяция (167), проектирование (162), поиск информации (162), уменьшение размерности (161), методы пространства состояний (159), статистические методы (158), регрессионный анализ (153), теория аппроксимации (152), сегментация изображений (152), процедуры (151), тензоры (148), магнитно-резонансная томография (146), статистика (146), цифровая память (145), вычислительные методы (143), химия (142), математические преобразования (141), алгоритмы обучения (140), кластеризация (139), информационные системы (139), оптимизация роя частиц (PSO) (139), теория множеств (139), биологическая модель (138), оценка (138), трехмерные (138), теория вычислений(133), многомерный анализ (133), квантовая теория (133), эволюционные алгоритмы (131), языки запросов (131), компьютерная графика (130), методы Монте-Карло (130), анализ данных (129), функции (126), сравнительное исследование (125), компьютерное зрение (125), улучшение изображения (124), моделирование (124), стохастические системы (124), теория графов (119), молекулярная динамика (119), прогнозирование (118), многочлены (118), наборы данных (117), восприятие (116), статистический анализ (116), анализ информации (115), марковские процессы (115), математические операторы (111), случайные процессы (111), цвет (110), модели биологические (105), восприятие пространства (105), спектральный анализ (105), нелинейные уравнения (104), прогнозирование (104), белки (104), динамика (103), реконструкция изображений (103), обработка информации (103), теория информации (в 103 документах). Ключевые слова определяют области применения методов исследования многомерных пространств.

По организациям, финансирующим спонсорам: National Natural Science Foundation of China (406); National Science Foundation (403); Российский фонд фундаментальных исследований (РФФИ) (138); National Institutes of Health (США, 119); Natural Sciences and Engineering Research Council of Canada (94 документа). По странам: США (4 556), Китай (1 548), Германия (1 105), РФ (1 038), Франция (949 документов). По типу источника: 11 007 статей в научных журналах, 3 538докладов в материалах конференций, 906 документов в книжных сериях, 267 книг. По языкам: 14 955 документов на английском, 316 на китайском, 178 на русском, 60 на французском, 57 на испанском языке. Обзор литературы и источников определяет изученность темы.

Вклад автора работы в решение проблемы

Автором информация о представлении многомерности пространств представлена в виде математических формул, образно-графического моделирования, текстовой информации.

Автором представлены алгоритмы создания четырехмерного куба.

Автор предложил гипотезу многомерности пространств.

Автор определил области возможного использования методов исследования многомерных пространств.

Введение понятий многомерности пространств

По существу пространство может иметь бесконечное количество измерений – от нулевого измерения до целочисленного n-измерения. Каждое пространство имеет n-ое количество осей и каждое тело в пространстве имеет n координат, чтобы точно определить, где находится тело. То есть в нулевом пространстве не будет осей, а значит, телу смысла нет задавать координаты, т. к. оно будет находиться в одном и том же месте в 0, то есть в одной точке. Следующее одномерное пространство определяется одной осью. Примерами одномерной оси могут служить ряд натуральных чисел, линейка, метка для бега или прыжков. Дальше идет двухмерное пространство или плоскость, которая задается двумя осями и двумя координатами. Примеры: декартова система координат, полотно для вышивки, экран монитора. Далее – трехмерное пространство, в котором мы находимся, задается тремя осями, и предмет можно задать тремя координатами. Примеры: наша вселенная или 3D графика.

Как видит наш глаз этот мир?

Наш мир, в котором мы находимся, называют трехмерным, потому что любой предмет можно задать тремя координатами: x, y, z или длина, ширина и высота. Но как мы видим наше трехмерное пространство? Видим мы двухмерно, то есть мы видим двухмерную проекцию трехмерного пространства. Наш глаз работает, как фотоаппарат, только фотоаппарат передает картинку на экран или фотографию, а наш глаз передает мозгу увиденную информацию. Если бы мы имели такую возможность, как трехмерное зрение, мы тогда могли заглядывать за предметы[1].

Представление двухмерной жизни

После того, как мы определили, как наш глаз видит этот мир, теперь надо представить, как бы придуманные нами существа жили и видели в более простом пространстве. Возьмем двухмерное пространство. Наблюдая сверху, мы бы увидели для них невидимые предметы, их устройство мира и их строение тела.

По аналогии с нами, они могут представлять двухмерно, но видеть будут одномерно, то есть одну линию. Попробуем пропустить через их двухмерное пространство, трехмерный куб. Они увидят удлиняющийся отрезок, а в их представлении это будет квадрат или треугольник переходящий в шестиугольник, в зависимости от того, как мы будем опускать данную простую фигуру.

Построение простых фигур в разных пространствах

Теперь уже перейдем к четырехмерному пространству и построим четырехмерную фигуру. Давайте построим четырехмерный гиперкуб тессеракт. Чтобы построить тессеракт, надо идти от простого к сложному. Мы можем построить материальную точку. Построим Рисунок 1.1. Следующее идет одномерное пространство. Из геометрии мы знаем, отрезок – это часть прямой, ограниченная двумя точками. Достроим из точки прямую. Получится Рисунок 1.2. После мы нарисуем такой же отрезок, который будет равен по длине и параллелен первому отрезку. Теперь их начало и концы соединим так, чтобы получился квадрат, как на Рисунке 1.3. Чтобы получить трехмерную фигуру, надо нарисовать такой же квадрат рядом с первоначально нарисованным, но только позади. Соединим вершины соответственно. Мы получили куб, изображенный на Рисунке 1.4. Рисунок 1.4 является двухмерной проекцией трёхмерной фигуры. Следующей фигурой будет гиперкуб. Если продолжить нашу алгоритмическую цепочку, то есть соединять вершину первой фигуры с вершиной второй фигуры соответственно, в данном случае мы будем соединять вершину одного куба с вершиной другого куба соответственно. После проделанного нами алгоритма мы получим четырехмерную фигуру - тессеракт, изображенный на Рисунке 1.5. Рисунок 1.5 является двухмерной проекцией трехмерной проекции четырехмерной фигуры.

исунок 1.1 – точка (нулевое пространство). Рисунок 1.2 – отрезок (одномерное пространство). Рисунок 1.3 – квадрат (двухмерное пространство). Рисунок 1.4 – куб (трёхмерное пространство). Рисунок 1.5 – тессеракт (четырехмерное пространство).

Наш глаз устроен так, что видит сначала передний план, а потом задний, а также для глаза передний план больше, чем задний план. Поэтому Рисунки 1.4 и 1.5 – это как бы фигуры, которые никогда не будут в таком положении для нашего глаза. Поэтому пойдем по алгоритму, первая фигура (составляющая будущей фигуры) будет передним планом, а вторая фигура будет задним планом, то есть первая фигура будет больше, чем вторая фигура. Начнем построение с фигуры, изображенной на Рисунке 2.3. Применяем данный и предыдущий алгоритмы и получим куб, изображенный на Рисунке 2.4. Строим гиперкуб, который получится, как на Рисунке 2.5. На Рисунке 2.5 помечены проведенные вершины, чтобы легче определить и представить, т. к. без выделения трудно будет найти куб в кубе.

исунок 2.1 – точка (нулевое пространство). Рисунок 2.2 – отрезок (одномерное пространство). Рисунок 2.3 – квадрат (двухмерное пространство). Рисунок 2.4 – куб (трехмерное пространство). Рисунок 2.5 – тессеракт (четырехмерное пространство).

На Рисунке 3 изображена трехмерная проекция тессеракта. На Рисунке 4 изображена развертка четырехмерного куба (тессеракта)

Если применять данный алгоритм, можно получить более сложные фигуры в более больших пространствах, например: пентеракт, хексеракт, хептеракт, октеракт, эненеракт и т. д.

Элементы гиперкуба

Многомерные пространства — миф или реальность? Большинству из нас, или, возможно, всем нам невозможно представить мир, состоящий из более чем трех пространственных измерений. Правильно ли утверждение, что такой мир не может существовать? Или просто человеческий разум не способен вообразить дополнительные измерения — измерения, которые могут оказаться такими же реальными, как и другие вещи, которые мы не можем увидеть?

Об авторах

Илья Щуров — кандидат физико-математических наук, доцент кафедры высшей математики НИУ ВШЭ.

Jason Hise — Physics programmer at Ready at Dawn Studios, 4D geometry enthusiast. Автор анимированных моделей, представленных в данной статье.

ashgrowen — пикабушник, проиллюстрировавший в этой статье построение тессеракта и гиперкуба.

Давайте начнем с простого — начнем с одномерного пространства. Представим себе, что у нас есть город, который расположен вдоль дороги, и в этом городе есть только одна улица. Тогда мы можем каждый дом на этой улице закодировать одним числом — у дома есть номер, и этот номер однозначно определяет, какой дом имеется в виду. Люди, которые живут в таком городе, — можно считать, что они живут в таком одномерном пространстве. Жить в одномерном пространстве довольно скучно, и люди обычно живут не в одномерном пространстве.

Вопрос: что такое четырехмерное пространство? Представить его себе не так-то просто, но можно думать о том, что это пространство, в котором каждая точка задается четырьмя числами. На самом деле мы с вами действительно живем в четырехмерном пространстве-времени, потому что события нашей жизни кодируются как раз четырьмя числами — помимо положения в пространстве, есть еще и время. Например, если вы назначаете свидание, то вы можете сделать это так: вы можете указать три числа, которые будут соответствовать точке в пространстве, и обязательно указать время, которое обычно задается в часах, минутах, секундах, но можно было бы закодировать его одним числом. Например, количество секунд, прошедших с определенной даты, — это тоже одно число. Таким образом получается четырехмерное пространство-время.

Представить себе геометрию этого четырехмерного пространства-времени не очень просто. Например, мы с вами привыкли к тому, что в нашем обычном трехмерном пространстве две плоскости могут пересекаться по прямой либо быть параллельными. Но не бывает такого, чтобы две плоскости пересекались в одной точке. Две прямые могут пересечься в одной точке, а на плоскости не могут в трехмерном пространстве. А в четырехмерном пространстве две плоскости могут и чаще всего пересекаются в одной точке. Можно представлять себе, хотя это уже совсем сложно, пространство большей размерности. На самом деле математики, когда работают с пространствами высокой размерности, чаще всего говорят просто: допустим, пятимерное пространство — это пространство, в котором точка задается пятью числами, пятью координатами. Безусловно, математики разработали разные методы, которые позволяют понимать что-то о геометрии такого пространства.

Почему это важно? Зачем понадобились такие пространства? Во-первых, четырехмерное пространство нам важно, потому что оно применяется в физике, потому что мы в нем живем. А зачем нужны пространства более высоких измерений? Давайте представим себе, что мы изучаем какие-то объекты, которые обладают большим количеством параметров. Например, мы изучаем страны, и у каждой страны есть территория, количество населения, внутренний валовой продукт, количество городов, какие-нибудь коэффициенты, индексы, что-нибудь такое. Мы можем представлять себе каждую страну в виде одной точки в каком-то пространстве достаточно высокой размерности. И оказывается, что с математической точки зрения это правильный способ об этом думать.

В частности, переход к геометрии многомерного пространства позволяет анализировать разные сложные объекты, обладающие большим количеством параметров.

Для того чтобы изучать такие объекты, используются методы, разработанные в науке, которая называется линейная алгебра. Несмотря на то, что она алгебра, на самом деле это наука о геометрии многомерных пространств. Конечно, поскольку представить их себе довольно тяжело, математики используют формулы, для того чтобы как раз изучать такие пространства.

Представить себе четырех-, пяти- или шестимерное пространство довольно сложно, но математики не боятся трудностей, и им мало даже стомерных пространств. Математики придумали бесконечномерное пространство — пространство, содержащее бесконечное количество измерений. В качестве примера такого пространства можно привести пространство всех возможных функций, заданных на отрезке или прямой.

Оказывается, что методы, которые были разработаны для конечномерных пространств, во многом переносятся и на случаи чрезвычайно сложных с точки зрения просто попытки их все представить пространств.

У линейной алгебры есть многочисленные приложения не только в математике, но и в самых разных науках, начиная c физики и заканчивая, например, экономикой или политической наукой. В частности, линейная алгебра является основой для многомерной статистики, которая как раз используется для вычленения связей между различными параметрами в каких-то массивах данных. В частности, популярный ныне термин Big Data зачастую связывается с решением задач по обработке данных, которые представляются именно большим количеством точек в пространстве какой-то конечной размерности. Чаще всего такие задачи можно переформулировать и разумно воспринимать именно в геометрических терминах.

Со школьных лет математика разделяется на алгебру и геометрию. Но на самом деле, если мы задумаемся о том, как устроена современная математика, то мы поймем, что те задачи, которые сейчас решаются, в частности, с применением методов линейной алгебры, на самом деле являются очень отдаленным продолжением тех задач, над которыми задумывались многие тысячи лет назад, например Пифагор или Евклид, разрабатывая ту самую школьную геометрию, которая сейчас есть в любом школьном учебнике. Удивительно, что задача по анализу больших данных оказывается в некотором смысле потомком, казалось бы, совсем бессмысленных — по крайней мере с практической точки зрения — упражнений древних греков по рисованию прямых или окружностей на плоскости или мысленному проведению прямых или плоскостей в трехмерном пространстве.

Тессерракт — четырехмерный куб

Чтобы ответить на эти вопросы, начнём с самого простого геометрического объекта — точки. Точка нульмерна. У неё нет ни длины, ни ширины, ни высоты.

Тессеракт — четырехмерный куб

Возьмём теперь отрезок и попробуем его сдвинуть так, как раньше точку. Можно представить себе, что наш отрезок — это основание широкой и очень тонкой кисти. Если мы выйдем за пределы прямой и будем двигаться в перпендикулярном направлении, получится прямоугольник. У прямоугольника есть два измерения — ширина и высота. Прямоугольник лежит в некоторой плоскости. Плоскость — это двумерное пространство (2D), на ней можно ввести двумерную систему координат — каждой точке будет соответствовать пара чисел. (Например, декартова система координат на школьной доске или широта и долгота на географической карте.).

Тессеракт — четырехмерный куб

На самом деле мы сталкиваемся с четырёхмерным пространством ежедневно: например, назначая свидание, мы указываем не только место встречи (его можно задать тройкой чисел), но и время (его можно задавать одним числом, например количеством секунд, прошедших с определенной даты). Если посмотреть на настоящий кирпич, у него есть не только длина, ширина и высота, но ещё и протяженность во времени — от момента создания до момента разрушения.

Физик скажет, что мы живём не просто в пространстве, а в пространстве-времени; математик добавит, что оно четырёхмерно. Так что четвёртое измерение ближе, чем кажется.

Представление других измерений

От 2D к 3D

Квадрат описывает его мир как плоскость, населенную линиями, кругами, квадратами, треугольниками и пятиугольниками.

Однажды перед квадратом появляется шар, но его суть он не может постичь, так как квадрат в своем мире может видеть только срез сферы, только форму двумерного круга.

Только после того, как сфера вытащит квадрат из его двумерного мира в свой трехмерный мир, он наконец поймет концепцию трех измерений. С этой новой точки зрения квадрат становится способен видеть формы своих соотечественников.

Принимая во внимание исключительность как жанра, который при некоторой фантазии и существовании иных его представителей, можно было бы назвать математическим романом, так и самой книги, её не хочется сильно ругать. Тем не менее, похвалы здесь заслуживает только лишь непривычность подачи, по духу близкая произведениям Льюиса Керрола, однако, в отличие от него, имеющая гораздо меньше точек соприкосновения с реальной жизнью. Данная книга, как верно отмечено в предисловии к изданию, не похожа ни на одну популяризацию, читателю, однако, не вполне ясно, по какой причине её сравнивают с популяризациями, потому как, хотя математические истины в ней, безусловно, затрагиваются, какой бы то ни было популяризацией книгу определённо считать невозможно. И вот почему: Перед вами уникальный пример объединения художественного вымысла с математическими идеями. И поклоннику математики, любящему читать, задумка изначально кажется замечательной: подобно математическим постулатам, ввести в рассмотрение ряд абстрактных объектов, наделить их определёнными свойствами, задать правила игры в описанном пространстве, а после, подражая опять же мысли исследователя, наблюдающего взаимодействия этих умозрительных объектов, проследить за их трансформацией. Но, так как книга всё же художественная, усилиям воли учёного места здесь не находится, поэтому для самодостаточности представленного на всеобщее обозрение мира объекты здесь наделяются сознанием и мотивацией для каких-либо взаимодействий друг с другом, после чего в прежде абстрактный мир оторванных от повседневной жизни чистых идей приносятся социальные взаимодействия с целым ворохом проблем, всегда сопутствующих всяким взаимоотношениям. Всевозможные трения, возникающие в книге на социальной почве, по мнению зрителя совершенно не нужны в книге: они практически не раскрыты и не могут восприниматься в серьезе, и в то же время отвлекают читателя от истинно тех вещей, ради которых написана книга. Даже принимая во внимания заверения обоих авторов о неспешности повествования, якобы более комфортную для читателя при приобретении каких-либо знаний (именно здесь приводится сравнение с популяризациями), зрителю темп повествования показался чрезвычайно затянутым и медлительным, а повторение одного и того же объяснения по несколько раз одними и теми же словами заставило усомниться в том, что рассказчик адекватно оценивает его умственным способности. И в конечном счёте неясно, для кого эта книга. Непривычным к математике людям описание в общем-то интересных явление в столь вольной форме вряд ли принесёт удовольствие, знакомым же с математикой ближе будет гораздо приятнее взять в руки качественную популяризацию, где величие и красоту математики не разбавляют плоскими сказками.

От 3D к 4D

Нам сложно принять эту идею, потому что, когда мы пытаемся представить даже одно дополнительное пространственное измерение — мы упираемся в кирпичную стену понимания. Похоже, что наш разум не может выйти за эти границы.

Представьте себе, например, что вы находитесь в центре пустой сферы. Расстояние между вами и каждой точкой на поверхности сферы равно. Теперь попробуйте двигаться в направлении, которое позволяет вам отойти от всех точек на поверхности сферы, сохраняя при этом равноудаленность. Вы не сможете этого сделать..

Житель Флатландии столкнулся бы с такой же проблемой, если бы он находился в центре круга. В его двумерном мире он не может находиться в центре круга и двигаться в направлении, которое позволяет ему оставаться равноудаленными каждой точке окружности круга, если только он не перейдет в третье измерение. Увы, у нас нет проводника в четырехмерное пространство как в романе Эббота, чтобы показать нам путь к 4D.

Одна из главных задач теоретической физики сегодня - поиск ответа на вопрос, существуют ли высшие измерения. Действительно ли пространство состоит лишь из длины, ширины и высоты или это лишь ограниченность человеческого восприятия? На протяжении тысячелетий ученые решительно отвергали идею существования многомерного пространства. Однако научно-техническая революция многое изменила, и сегодня наука уже не так категорична в вопросе высших измерений.

В чем сущность понятия "многомерное пространство"?

Человек живет в мире, который состоит из трех измерений. Координаты любого объекта можно выразить тремя значениями. А иногда и двумя - если речь идет о том, что находится на поверхности Земли.

Посредством длины, ширины и высоты можно описать как земные объекты, так и небесные тела - планеты, звезды и галактики. Хватает их и для вещей, населяющих микромир, - молекул, атомов и элементарных частиц. Четвертым измерением принято считать время.

В многомерном пространстве должно быть как минимум пять измерений. Современная теоретическая физика выработала множество теорий для пространств с разной размерностью - вплоть до 26. Есть также теория, описывающая пространство с бесконечным количеством измерений.

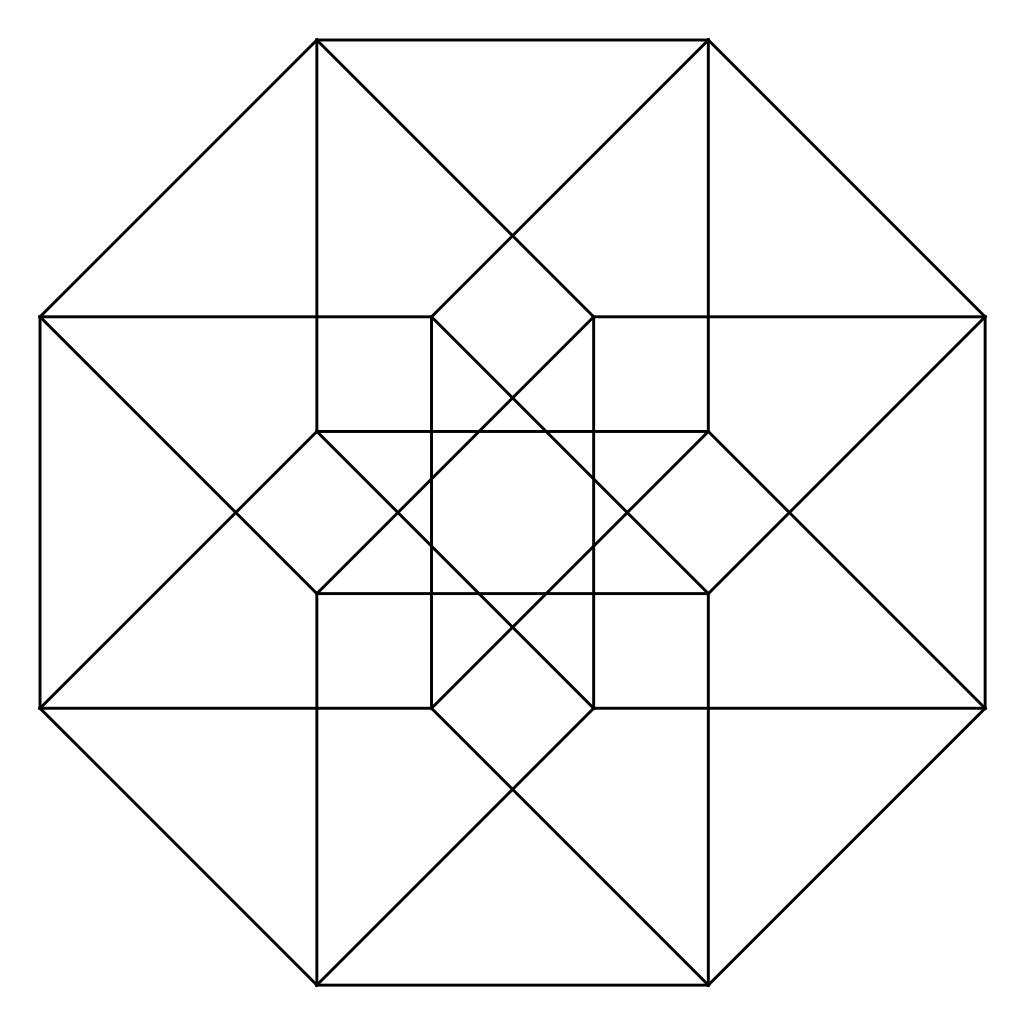
От Евклида до Эйнштейна

Физики и математики Античности, Средних веков и Нового времени категорически отрицали возможность существования высших измерений. Некоторые математики даже выводили обоснования ограниченности пространства тремя параметрами. Евклидова геометрия предполагала наличие лишь трех измерений.

До появления общей теории относительности ученые вообще считали многомерное пространство предметом, недостойным изучения и выдвижения теорий. Когда же Альберт Эйнштейн сформулировал понятия пространства-времени, объединив три измерения с четвертым, временным, определенность в этом вопросе тут же исчезла.

Теория относительности доказывает, что время и пространство не являются отдельными и независимыми вещами. Например, если космонавты сядут на корабль, который будет долго двигаться на высокой скорости, то по возвращении на Землю они окажутся моложе своих ровесников. Причина в том, что для них пройдет меньше времени, чем для людей на Земле.

Теория Калуцы-Клейна

В 1921 году немецкий математик Теодор Калуца с помощью уравнений теории относительности создал теорию, которая впервые объединила гравитацию и электромагнетизм. Согласно этой теории, пространство имеет пять измерений (в том числе время).

В 1926 году шведский физик Оскар Клейн вывел обоснование невидимости пятого измерения, описанное Калуцой. Оно заключалось в том, что высшие измерения сжаты до невероятно малой величины, которая называется планковской и составляет 10 -35 . Впоследствии это легло в основу других теорий многомерного пространства.

Теория струн

Это направление теоретической физики на сегодняшний день наиболее перспективное. Теория струн претендует на звание того, что физики ищут с самого появления общей теории относительности. Это так называемая теория всего.

Дело в том, что два фундаментальных физических принципа - теория относительности и квантовая механика - находятся в неразрешимом противоречии друг с другом. Теория всего - гипотетическая концепция, которая смогла бы объяснить этот парадокс. В свою очередь, теория струн больше других подходит на эту роль.

Суть ее в том, что на субатомном уровне строения мира происходит колебание частиц, похожее на колебание обычных струн, например, скрипки. Отсюда теория и получила свое название. Причем размеры этих струн чрезвычайно малы и колеблются в районе планковской длины - той самой, что фигурирует в теории Калуцы-Клейна. Если увеличить атом до размеров галактики, то струна достигнет лишь размеров взрослого дерева. Теория струн работает лишь в многомерном пространстве. Причем существует несколько ее версий. Одни требуют 10-мерного, а другие - 26-мерного пространства.

На момент своего возникновения теория струн воспринималась физиками с большим скептицизмом. Но сегодня она является наиболее популярной, и ее разработкой занимаются многие физики-теоретики. Однако доказать положения теории экспериментально пока что не представляется возможным.

Гильбертово пространство

Еще одна теория, описывающая высшие измерения, - гильбертово пространство. Его описал немецкий ученый-математик Давид Гильберт при работе над теорией интегральных уравнений.

Гильбертово пространство - математическая теория, которая описывает свойства евклидова пространства в бесконечной размерности. То есть это многомерное пространство с бесчисленным количеством измерений.

Гиперпространство в фантастике

Идея многомерного пространства вылилась во множество сюжетов научной фантастики - как литературной, так и кинематографической.

Так, в тетралогии Дэна Симмонса "Песни Гипериона" человечество использует сеть гиперпространственных нуль-порталов, способных мгновенно переносить объекты на далекое расстояние. В романе Роберта Хайнлайна "Звездный десант" солдаты также используют гиперпространство для перемещений.

Идея гиперпространственных полетов была использована во многих фильмах космической оперы, в том числе знаменитой саге "Звездные войны" и сериале "Вавилон-5".

Сюжет фильма "Интерстеллар" практически полностью завязан на идее высших измерений. В поисках пригодной планеты для колонизации герои путешествуют в космосе через червоточины - гиперпространственный туннель, ведущий в другую систему. А ближе к концу главный герой попадает в мир многомерного пространства, с помощью которого ему удается передать информацию в прошлое. В фильме также четко показана связь пространства и времени, выведенная Эйнштейном: для космонавтов время идет медленнее, чем для персонажей на Земле.

В фильме "Куб 2: Гиперкуб" герои оказываются внутри тессеракта. Так в теории высших измерений называется многомерный куб. В поисках выхода они попадают в параллельные вселенные, где встречают свои альтернативные версии.

Идея многомерного пространства по-прежнему остается фантастичной и недоказанной. Однако сегодня она гораздо ближе и реальнее, чем несколько десятилетий назад. Вполне возможно, в ближайшее столетие ученые обнаружат способ передвигаться в высших измерениях и, следовательно, путешествовать в параллельных мирах. А до тех пор люди будут много фантазировать на эту тему, выдумывая удивительные истории.

У линейной алгебры есть многочисленные приложения не только в математике, но и в самых разных науках, начиная c физики и заканчивая, например, экономикой или политической наукой. В частности, линейная алгебра является основой для многомерной статистики, которая как раз используется для вычленения связей между различными параметрами в каких-то массивах данных. В частности, популярный ныне термин Big Data зачастую связывается с решением задач по обработке данных, которые представляются именно большим количеством точек в пространстве какой-то конечной размерности. Чаще всего такие задачи можно переформулировать и разумно воспринимать именно в геометрических терминах.

Читайте также: