Доклад на тему натуральные логарифмы и число е

Обновлено: 28.04.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Цель: исследовать в каких областях науки, техники нашли применение логарифмы, логарифмическая функция.

На протяжении 16 века быстро возрастало количество приближенных вычислений, прежде всего, в астрономии. Совершенствование инструментов, исследование планетных движений и другие работы потребовали колоссальных, иногда многолетних, расчетов. Астрономам грозила реальная опасность утонуть в невыполненных расчетах.

С точки зрения вычислительной практики, изобретение логарифмов по возможности можно смело поставить рядом с другими, более древним великим изобретением индусов – нашей десятичной системы нумерации.

Через десяток лет после появления логарифмов Непера английский ученый Гунтер изобрел очень популярный прежде счетный прибор – логарифмическую линейку. Она помогала астрономам и инженерам при вычислениях, она позволяла быстро получать ответ с достаточной точностью в три значащие цифры.

Таким образом, потребность в сложных расчётах быстро росла. Теория логарифмов связана с именами целого ряда математиков: Генри Бригс, Эдмунд Уингейт, Уильям Отред, Н. Меркатор, Джон Спейдел, К. Бремикер, Ф. Клейн.

Анализ тематики создание логарифмов достаточно актуален и представляет научный и практический интерес.

Цель: исследовать в каких областях науки, техники нашли применение логарифмы, логарифмическая функция.

Задача: 1. Актуализация практической значимости математических знаний;

2. Развитие нравственных представлений о природе математики, сущности и происхождении математической абстракции.

Проблема: показать практическую значимость логарифмов для окружения.

Основная часть

История логарифма

Логарифмы были изобретены не позднее 1594 года независимо друг от друга шотландским бароном Непером (1550-1617) и через десять лет швейцарским механиком Бюрги (1552-1632). Оба хотели дать новое удобное средство арифметических вычислений, хотя подошли они к этой задаче по-разному. Непер кинематически выразил логарифмическую функцию и, тем самым, вступил в новую область теории функции. Бюрги остался на почве рассмотрения дискретных прогрессий. Впрочем, определение логарифма у обоих не похоже на современное.

В ходе тригонометрических расчётов, Неперу пришла в голову идея: заменить трудоёмкое умножение на простое, сложение, сопоставив с помощью специальных таблиц геометрическую и арифметическую прогрессии, при этом геометрическая будет исходной.

Сочинение было разделено на 2 книги, из которых первая посвящена логарифмам, а вторая — плоской и сферической тригонометрии, причём вторая часть одновременно служит практическим пособием по первой. Более развёрнутое, описание содержалось в другом труде, изданном посмертно его сыном; там же Непер пояснил, как он составлял свои таблицы.

Понятия функции тогда ещё не было, и Непер определил логарифм кинематически, сопоставив равномерное и логарифмически-замедленное движение. В современной записи модель Непера можно изобразить дифференциальным уравнением: dx/x = -dy/M, где M — масштабный множитель, введенный для того, чтобы значение получилось целым числом с нужным количеством знаков (десятичные дроби тогда ещё не нашли широкого применения). Непер взял M = 10000000.

Строго говоря, Непер табулировал не ту функцию, которая сейчас называется логарифмом.

К сожалению, все значения таблицы Непера содержали вычислительную ошибку после шестого знака. Однако это не помешало новой методике вычислений получить широчайшую популярность, и составлением логарифмических таблиц занялись многие европейские математики, включая Кеплера.

В 1615 году в беседе с профессором математики Грешем Колледжа в Лондоне Генри Бригсом (1561-1631) Непер предложил принять за логарифм единицы нуль, а за логарифм десяти - 100, или, что сводится к тому же, просто 1. Так появились десятичные логарифмы и были напечатаны первые логарифмические таблицы. Непер уже был болен, поэтому не смог усовершенствовать свои таблицы, однако дал Бригсу рекомендации видоизменить определение логарифма, приблизив его к современному. Бригс опубликовал свои таблицы в год смерти Непера (1617).

Позже таблицы Бригса дополнил голландский книготорговец и любитель математики Андриан Флакк (1600-1667). Непер и Бригс, хотя пришли к логарифмам раньше всех, опубликовали свои таблицы позже других - в 1620 году.

Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Вега́ появилось только в 1857 году в Берлине (таблицы Бремивера).

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — незаменимый инструмент инженера.

Знаки log и Log были введены в 1624 году И. Кеплером.

На русском языке первые логарифмические таблицы были изданы в 1703 году. Но во всех логарифмических таблицах были допущены ошибки при вычислении. Первые безошибочные таблицы вышли в 1857 году в Берлине в обработке немецкого математика К. Бремикера (1804-1877).

Дальнейшее развитие теории логарифмов связано с более широким применением аналитической геометрии и исчисления бесконечно малых. К тому времени относится установление связи между квадратурой равносторонней гиперболы и натуральным логарифмом.

С открытием логарифмического ряда изменилась техника вычисления логарифмов: они стали определяться с помощью бесконечных рядов.

Таким образом, прошло 394 года с тех пор, как логарифмы впервые были введены (считая с 1614 г.), прежде чем математики пришли к определению понятия логарифма, которое положено теперь в основу школьного курса.

Логарифмические таблицы

Если вычислительные потребности практической жизни и технического обихода вполне обеспечиваются трех и четырехзначными таблицами то с другой стороны, к услугам теоретического исследователя имеются таблицы и с гораздо большим числом знаков, чем даже 14- значные логарифмы. Вообще говоря, логарифм в большинстве случаев есть число иррациональное и не может быть точно выражен никаким числом цифр; логарифмы большинства чисел, сколько бы знаков ни брать, выражаются лишь приближенно, тем точней, чем больше цифр в их мантиссе. Для научных работ оказывается иногда недостаточной точность 14- значных логарифмов, но среди пятисот всевозможных образов логарифмических таблиц вышедших в свет, со времени их изобретения, исследователь всегда найдет такие, которые его удовлетворяют. Например, 20- значные логарифмы чисел от 2 до1200, изданные во Франции Кале.

Для еще более ограниченной группы чисел имеются таблицы логарифмов с огромным числом десятичных знаков - настоящие логарифмические диковинки о существование которых не подозревают многие математики.

Вот эти логарифмы – исполины все они - не десятичные, а натуральные: (натуральными называются логарифмы, вычисленные не при основании 10, а при основании 2,718…, о котором у вас еще будет речь впереди. 48–значные таблицы Вольфрама для чисел до 10000; 61-значные таблицы Шарпа; 102-значные таблицы Паркхерста.

Счетная линейка

Логарифмическая спираль

Логарифмическая спираль - плоская трансцендентная кривая, уравнение которой в полярных координатах имеет вид p=a φ, a0.

Рога козлов, раковина улитки и семечки в подсолнухе закручены по логарифмической спирали

Применение логарифмов в различных сферах жизнедеятельности человека

Радиоактивный распад. Изменение массы радиоактивного вещества происходит по формуле , где m ₀ – где масса вещества в начальный период времени t=0, m – масса вещества в момент времени t, .
T - период полураспада. Это означает, что через время Т после начального момента времени, масса радиоактивного вещества уменьшается вдвое.

Народонаселение. Изменение количества людей в стране на небольшом отрезке времени с хорошей точностью описывается формулой , где N ₀ – число людей при t=0, N – число людей в момент t, λ – некоторая константа.

Формула Циолковского. Эта формула, связывающая скорость ракеты V с ее массой m: , где Vr – скорость вылетающих газов, m ₀ – стартовая масса ракеты. Скорость истечения газа при сгорании топлива Vr невелика (в настоящее время она меньше или равна 2 км/с). Логарифм растет очень медленно, и для того чтобы достичь космической скорости, необходимо сделать большим отношение , т.е. почти всю стартовую массу отдать под топливо.

Звукоизоляция стен. Коэффициент звукоизоляции стен измеряется по формуле , где p ₀ – давление звука до поглощения, p – давление звука, прошедшего через стену, А – некоторая константа, которая в расчетах принимается равной 20 децибелам. Если коэффициент звукоизоляции D равен, например 20 децибел, то это означает, что и p ₀ =10p, т.е. стена снижает давление звука в 10 раз. Такую изоляцию имеет деревянная дверь.

Логарифмы в музыке.

Номера клавишей рояля представляют собой логарифмы чисел – колебаний соответствующих звуков (умноженные на 12).

Мы даже можем сказать, что номер октавы представляет собой целую часть (характеристику) логарифма числа колебаний этого тона, а номер звука в данной октаве, деленный на 12 – дробную часть (мантиссу) этого логарифма.

Логарифмы в поэзии

Многообразные применения показательной (или её ещё называют, экспоненциальной) функции вдохновили английского поэта Элмера Брила на написание “Оды экспоненте”, отрывок из которой гласит:

Собрала для вас похожие темы рефератов, посмотрите, почитайте:

Введение

Десятичный логарифм называется логарифмом на основе 10. Он обозначен lg, т.е. журнал 10 N = lg N . Логариты чисел 10, 100, 1000,… соответственно равны 1, 2, 3, … т.е. имеют столько же положительных единиц, сколько и нулей после единиц нулей в логарифмическом числе.

Логарифмы чисел 0.1, 0.01, 0.001,… соответственно равны -1, -2, -3, …, т.е. имеют столько же отрицательных единиц, сколько и нулей в логарифмическом числе перед единицей (счет и ноль целых чисел). Логариты других чисел имеют дробную часть, называемую мантисса. Вся часть логарифма называется мантисса. Десятичные логарифмы наиболее удобны для практического использования.

Натуральный логарифм

LOGARIFM, число, применение которого упрощает многие сложные арифметические операции. Использование его логарифмов вместо чисел в вычислениях позволяет заменить умножение на более простую операцию сложения, деление на вычитание, увеличение на умножение, извлечение корня на деление.

Общее описание. Логарифм заданного числа — это индикатор того, в какой степени для получения заданного числа необходимо поднять другое число, называемое основой логарифма. Например, логарифм числа 100 основан на 10 2. Другими словами, 10 должно быть поднято в квадрате, чтобы получить число 100 (102 = 100). Если n — заданное число, b — база и l — логарифм, то bl = n. Число n также называется антилогарифмом к основанию b числа l. Например, антилогарифм 2 на основе 10 равен 100, который можно записать как отношение logb n = l и антилогаб l = n.

Любое положительное число, кроме одного, может служить основой логарифмов, но, к сожалению, получается, что если b и n — рациональные числа, то в редких случаях такое рациональное число l существует, что bl = n. Однако, иррациональное число l может быть определено, например, так, что 10l = 2; это иррациональное число l может быть аппроксимировано рациональными числами с любой желаемой точностью.

Получается, что в данном примере l примерно равно 0.3010, и это приблизительное значение логарифма на основе 10 числа 2 можно найти в четырехзначных таблицах с десятичными логарифмами. Логарифмы, основанные на 10 (или десятичных логарифмах), так часто используются в вычислениях, что называют обычные логарифмы и отмечают их как log2 = 0.3010 или lg2 = 0.3010, без явного указания базы логарифмов. Логариты, основанные на e, трансцендентальном числе, соответствующем приблизительно 2.71828, называются натуральными логаритами. В основном они встречаются в работах по математическому анализу и его применению в различных науках. Естественные логарифмы также записываются без явного указания базы, но со специальным обозначением ln: например, ln2 = 0.6931, как, например, 0.6931 = 2. См. такжеNUMBERe.

Использование таблиц с общими логарифмами

Обычный логарифм числа — это мера степени, до которой 10 должно быть возведено, чтобы получить определенное число. Так как 100 = 1, 101 = 10 и 102 = 100, то мы сразу получаем этот log1 = 0, log10 = 1, log100 = 2 и т.д. за рост целых 10 градусов. Аналогично, 10-1 = 0.1, 10-2 = 0.01 и, следовательно, log0.1 = -1, log0.01 = -2 и т.д. для всех отрицательных целых градусов 10. Обычные логарифмы остальных чисел закрываются между логарифмами ближайших целых градусов числа 10; log2 должен быть закрыт между 0 и 1, log20 между 1 и 2 и log0.2 между -1 и 0. Таким образом, логарифм состоит из двух частей, целое число и десятичная дробь, закрытая между 0 и 1. Целая часть называется характеристикой логарифма и определяется самим числом, дробная часть называется мантиссой и может быть найдена в таблицах. Дополнительно: log20 = log(2ґ10) = log2 + log10 = (log2) + 1. Таким образом, логарифм числа 2 равен 0.3010.

log20 = 0.3010 + 1 = 1.3010. Аналогично log0.2 = log(2yo10) = log2 — log10 = (log2) — 1 = 0.3010 — 1. После вычитания получаем log0.2 = — 0.6990.

Однако более удобно представлять log0.2 как 0.3010 — 1 или как 9.3010 — 10; можно также сформулировать общее правило: все числа, полученные из заданного числа путем умножения со степенью числа 10, имеют одинаковые мантиссы, соответствующие мантиссе заданного числа. Большинство таблиц содержат мантиссы чисел в диапазоне от 1 до 10, так как все остальные числа могут быть взяты из мантисс, приведенных в таблице.

В большинстве таблиц используются логарифмы с четырьмя или пятью знаками после запятой, хотя существуют также семизначные таблицы и таблицы с еще большим количеством символов. Самый простой способ научиться пользоваться такими таблицами — это использовать примеры. Чтобы найти log3.59, сначала обратите внимание, что число 3.59 заключено между 100 и 101, поэтому его характеристика равна 0. В таблице (слева) мы находим число 35 и двигаемся вдоль строки к столбцу, в котором сверху стоит число 9; на пересечении этого столбца и строки 35 находится число 5551, поэтому log3.59 = 0.5551. Чтобы найти мантиссу числа с четырьмя значащими цифрами, нужно использовать интерполяцию. В некоторых таблицах интерполяцию облегчают пропорциональные пропорции, приведенные в последних девяти столбцах справа от каждой страницы таблицы. Теперь найдем log736.4, номер 736.4 между 102 и 103, так что характеристика его логарифма — 2. В таблице мы находим строку слева от нее 73 и столбец 6. На пересечении этой строки и этого столбца — номер 8669. Среди линейных частей мы находим столбец 4. На пересечении 73-й строки и столбца 4 — номер 2. Прибавив 2 к 8669, мы получаем мантиссу — она равна 8671, поэтому log736.4 = 2.8671.

Натуральные логарифмы

Таблицы и свойства природных логарифмов схожи с таблицами и свойствами обычных логарифмов. Основное различие между ними и другими заключается в том, что целочисленная часть натурального логарифма не значима при определении положения десятичной точки, и поэтому разница между мантиссой и признаком не важна. Натуральные логарифмы чисел 5.432; 54.32 и 543.2 равны 1.6923; 3.9949 и 6.2975. Связь между этими логарифмами становится очевидной при рассмотрении различий между ними: log543.2 — log54.32 = 6.2975 — 3.9949 = 2.3026; последнее число является ничем иным, как естественным логарифмом числа 10 (написано следующим образом: ln10); log543.2 — log5.432 = 4.6052; последнее число — 2ln10. Но 543.2 = 10ґ54.32 = 102ґ5.432. Так можно найти на натуральном логарифме данного числа натуральные логарифмы чисел, соответствующие произведениям числа a на любой градус n числа 10 путем сложения lna ln10 умноженного на n, т.е. ln(aґ10n) = lna + nln10 = lna + 2.3026n. Например: ln0.005432 = ln(5.432ґ10-3) = ln5.432 — 3ln10 = 1.6923 — (3ґ2.3026) = — 5.2155. Поэтому таблицы натуральных логарифмов, как и таблицы обычных логарифмов, обычно содержат только логарифмы чисел от 1 до 10. В системе натуральных логарифмов можно говорить об антилогарифмах, но чаще всего мы говорим об экспоненциальной функции или экспоненте. Если x = lny, то y = ex, а y называется показателем x (для упрощения шрифтового шрифта часто пишется y = exp x). Экспонент играет роль антилогарифма числа x.

Заключение

Используя таблицы с десятичными и натуральными логарифмами, можно создавать таблицы с логарифмами на основе, отличной от 10 и e. Если logb a = x, то bx = a, а значит logc bx = logc a или xlogc b = logc a или x = logc a/logc b = logb a. Следовательно, эту формулу можно использовать для построения логарифмических таблиц из таблицы логарифмов для базы c для любой другой базы b. Множитель 1/logc b называется модулем для получения из базы c в базу b. Ничто не мешает, например, использовать формулу для обработки или перехода от одной системы логарифмов к другой, найти естественные логарифмы из таблицы общих логарифмов или осуществить обратный переход. Например: log105,432 = логе 5,432/логе 10 = 1,6923/2,3026 = 1,6923ґ0,4343 = 0,7350. Число 0,4343, на которое необходимо умножить натуральный логарифм данного числа, чтобы получить обычный логарифм, является модулем перехода к системе обычных логарифмов.

Список литературы

Образовательный сайт для студентов и школьников

Название введено Непером, происходит от греческих слов logoz и ariumoz - оно означает буквально “числа отношений”. Логарифмы были изобретены Непером. Непер изобрел логарифмы не позднее 1594 года. Логарифмы с основанием a ввел учитель математики Спейдел. Слово основание заимствовано из теории о степенях и перенесено в теорию логарифмов Эйлером. Глагол “логарифмировать” появился в 19 веке у Коппе. Коши первый предложил ввести различные знаки для десятичных и натуральных логарифмов. Обозначения, близкие к современным ввел немецкий математик Прингсхейм в 1893 году. Именно он обозначал логарифм натурального числа через ln . Определение логарифма как показателя степени данного основания можно найти у Валлиса (1665 год), Бернулли (1694 год).

Определение логарифма

Логарифмом числа b>0 по основанию a>0, a ≠ 1 , называется показатель степени, в которую надо возвести число a, чтобы получить число b.

Логарифм числа b по основанию a обозначается: log_a b

Основное логарифмическое тождество

Это равенство является просто другой формой определения логарифма. Его часто называют основным логарифмическим тождеством.

1. 3=log₂ 8, так как 2³=8

2. ½=log₃ √3 , так как 3= √3

3. 3 log 3 1/5 =1/5

Натуральный и десятичный логарифмы

Натуральным называется логарифм, основание которого равно e. Обозначается ln b, т.е.

Десятичным называется логарифм, основание которого равно 10. Обозначается lg b, т.е.

Основные свойства логарифмов

Пусть: a > 0, a ≠ 1. Тогда:

1. log_a x*y=logax+logay (x>0, y>0)

2. log_a y/x=logax−logay (x>0, y>0)

3. log_a x p =p*logax (x>0)

Формы перехода от логарифма по одному основанию к логарифмы по другому основанию

Логарифмические уравнения

1) Уравнение содержащие переменную под знаком логарифма (log) называются логарифмическими. Простейшим примером логарифмического уравнения служит уравнение вида: log_a x=b, где а>0 и а=1.

2) Решение логарифмического уравнения вида: log_a f(x)=log_a g(x) (1) основано на том, что оно равносильно уравнению вида f(x) = g(x) (2) при дополнительных условиях f(x)>0 и g(x)>0.

3) При переходе от уравнения (1) к уравнению (2) возможно появление посторонних корней поэтому для них выявления требуется проверка.

4) При решении логарифмических уравнений часто используется метод подстановки.

Логарифм число, применение которого позволяет упростить многие сложные операции арифметики. Использование в вычислениях вместо чисел их логарифмов позволяет заменить умножение более простой операцией сложения, деление - вычитанием, возведение в степень - умножением и извлечение корней - делением.

В данном видеоуроке мы познакомимся с понятиями десятичного и натурального логарифмов. Выясним, как вычисляют логарифмы при помощи калькулятора и таблиц логарифмов. А также научимся переходить от логарифма по одному основанию к логарифму по другому основанию.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока "Десятичные и натуральные логарифмы"

При решении логарифмов пока мы с вами сталкивались лишь с логарифмами, у которых были одинаковые основания.

Однако, зачастую приходится искать значения выражений, которые составлены из логарифмов по разным основаниям.

…

Заметим, что действия с логарифмами возможны только при одинаковых основаниях!

Тогда как поступают, если основания у логарифмов разные? Что нужно сделать, чтобы найти значения таких выражений? Так вот для этого вводятся десятичные и натуральные логарифмы, а также формула перехода от логарифма по одному основанию к логарифму по другому основанию.

Среди различных оснований для вычисления логарифмов чаще всего используется число 10. Логарифмы по такому основанию называют десятичными. Другими словами, десятичный логарифм числа есть решение уравнения

Что же касается натурального логарифма числа, то так называют логарифм этого числа по основанию , где – иррациональное число, приближённо

Кстати, иррациональное число е играет важную роль в математике и её приложениях. Число е можно представить как сумму:

……

Все свойства, которые мы рассматривали для логарифмов по произвольному основанию, справедливы для десятичного и натурального логарифмов.

1., . 1., .

2. . 2. .

3. . 3. .

4. , , . 4. , , .

5. , , . 5. , , .

6. , , . 6. , , .

7. , , . 7. , , .

А теперь давайте разберёмся, как вычисляют десятичный и натуральный логарифмы. Проще всего значение логарифма можно найти с помощью инженерного калькулятора.

Давайте посмотрим, как находят значения следующих логарифмов при помощи инженерного калькулятора: ; .

Найдём значение десятичного логарифма числа .

На практике, конечно, мы округлим это число до нужного разряда.

Ранее мы с вами уже говорили, что с появлением логарифмов многие учёные занялись составлением логарифмических таблиц. Так, например, первые таблицы десятичных логарифмов для чисел от 1 до 1000 опубликовал в 1617 году оксфордский профессор математики Генри Бригс, с восемью (позже — с четырнадцатью) знаками.

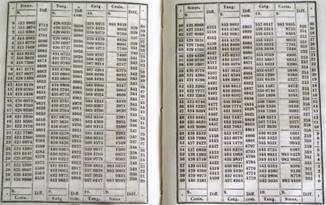
Давайте рассмотрим принцип использования такой таблицы на примере двузначной таблицы десятичных логарифмов. На экране вы видите таблицу, в которой указаны значения десятичных логарифмов чисел от 1 до .

Левый столбец таблицы отвечает за число целых, а верхняя строка – за число десятых. Давайте найдём значение .

Итак, значение этого логарифма будет расположено на пересечении строки с числом 7 целых и столбца с числом 3 десятых. Как видим, значение нашего логарифма совпало с ранее найденным нами при помощи инженерного калькулятора, оно .

А теперь найдём значение при помощи таблицы натуральных логарифмов российского математика Брадиса.

На экране вы видите таблицу, в которой указаны значения натуральных логарифмов чисел от 1 до 99. Здесь левый столбец таблицы отвечает за число десятков, а верхняя строка – за число единиц.

Итак, значение будет расположено на пересечении строки с числом 1 и столбца с числом 5. Как видим, значение нашего логарифма совпало с ранее найденным нами при помощи инженерного калькулятора, оно приближённо равно .

А как же быть с вычислением логарифмов по другим основаниям? Ведь при помощи инженерного калькулятора и таблиц логарифмов мы вычисляли только значения десятичных и натуральных логарифмов. Оказывается, достаточно знать значения только десятичных и натуральных логарифмов чисел, чтобы находить логарифмы чисел по любому основанию. Для этого используют формулу перехода от логарифма по одному основанию к логарифму по другому основанию.

Сейчас мы её с вами выведем. Итак, пусть .

Перейдём к показательной форме записи этого равенства, то есть получим .

Теперь прологарифмируем это равенство по основанию с. Другими словами, найдём логарифмы с основанием обеих частей этого равенства. Получим:.

Применим к левой части равенства свойство логарифма степени, получим .

Теперь разделим обе части равенства на . Получим .

Так как , то имеем .

Получившееся равенство и есть формула перехода от логарифма по одному основанию к логарифму по другому основанию.

Отметим, что эта формула верна, если выполняются следующие условия:

, , , , .

Из формулы перехода от логарифма по одному основанию к логарифму по другому основанию следует формула .

Также из формулы перехода от логарифма по одному основанию к логарифму по другому основанию при и при получаются формулы перехода к десятичным и натуральным логарифмам.

А теперь давайте приступим к практической части нашего урока.

Задание 1. Найдите значение .

Исходя из формулы , имеем логарифм

При помощи калькулятора вычислим значения десятичного – оно

и .

Подставим найденные значения в формулу перехода. Получим, что .

Читайте также: