Доклад на тему эллипс 6 класс геометрия
Обновлено: 06.05.2024
Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.
Определение и элементы эллипса
Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.
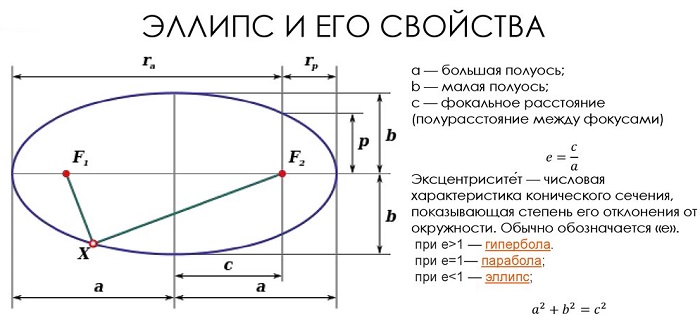
По форме график эллипса представляет замкнутую овальную кривую:
Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.
Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.
Точки эллипса, являющиеся концами осей, называются вершинами.
Расстояния от точки на линии до фокусов получили название фокальных радиусов.
Расстояние между фокусами есть фокальное расстояние.
Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.
Основные свойства эллипса
имеются две оси и один центр симметрии;
при равенстве полуосей линия превращается в окружность;
все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.
Уравнение эллипса
Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.

Для составления уравнения достаточно воспользоваться определением, введя обозначение:
а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);
c – половина фокального расстояния;
M(x;y) – произвольная точка линии.
В этом случае фокусы находятся в точках F1(-c;0); F2(c;0)


После ввода ещё одного обозначения
получается наиболее простой вид уравнения:
a 2 b 2 - a 2 y 2 - x 2 b 2 = 0,
a 2 b 2 = a 2 y 2 + x 2 b 2 ,
Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).
В случае (b b) формула эксцентриситета (ε) принимает вид:
Чем меньше эксцентриситет, тем более сжатым будет эллипс.
Площадь эллипса
Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:

a – большая полуось, b – малая.
Площадь сегмента эллипса
Часть эллипса, отсекаемая прямой, называется его сегментом.
![]()
Длина дуги эллипса
Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:
![]()
Радиус круга, вписанного в эллипс
В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:
Радиус круга, описанного вокруг эллипса
Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:
Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.
Как построить эллипс
Построение линии удобно выполнять в декартовых координатах в каноническом виде.
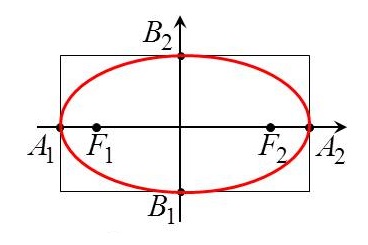
![]()
Строится прямоугольник. Для этого проводятся прямые:
![]()
Сглаживая углы, проводится линия по сторонам прямоугольника.
Полученная фигура есть эллипс. По координатам отмечается каждый фокус.
При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.

№ слайда 2
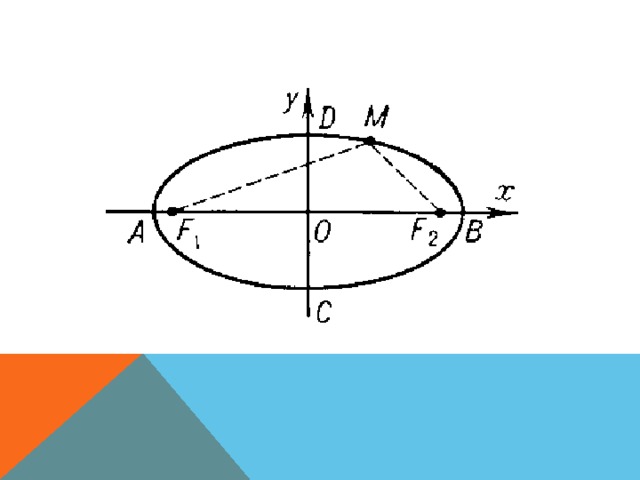
ЧТО ЖЕ ТАКОЕ ЭЛЛИПС Геометрическое место точек плоскости, сумма расстояний от которых до двух заданных точек F1, F2 есть величина постоянная, называется эллипсом. Точки F1, F2 называются фокусами эллипса.
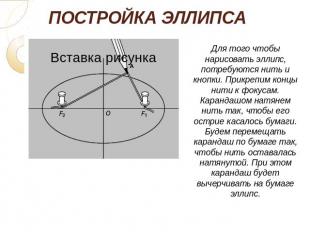
№ слайда 3
ПОСТРОЙКА ЭЛЛИПСА Для того чтобы нарисовать эллипс, потребуются нить и кнопки. Прикрепим концы нити к фокусам. Карандашом натянем нить так, чтобы его острие касалось бумаги. Будем перемещать карандаш по бумаге так, чтобы нить оставалась натянутой. При этом карандаш будет вычерчивать на бумаге эллипс.

№ слайда 4
КАСАТЕЛЬНАЯ Касательной к эллипсу называется прямая, имеющая с эллипсом только одну общую точку. Общая точка называется точкой касания.Пусть A – произвольная точка эллипса с фокусами F1, F2. Тогда касательной к эллипсу, проходящей через точку A, является прямая, содержащая биссектрису угла, смежного с углом F1AF2

№ слайда 5
ИНТЕРЕСНЫЕ ФАКТЫ Оказывается, что все планеты движутся вокруг Солнца не по кругу, а по эллипсу.Кратеры на Луне также имеют форму эллипса.Наш единственный спутник Луна производит вращение вокруг Земли по эллиптической орбите с периодом 27,32 суток.

№ слайда 6


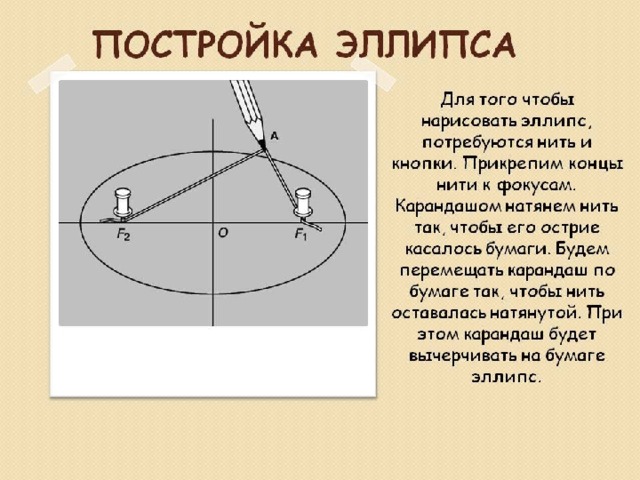
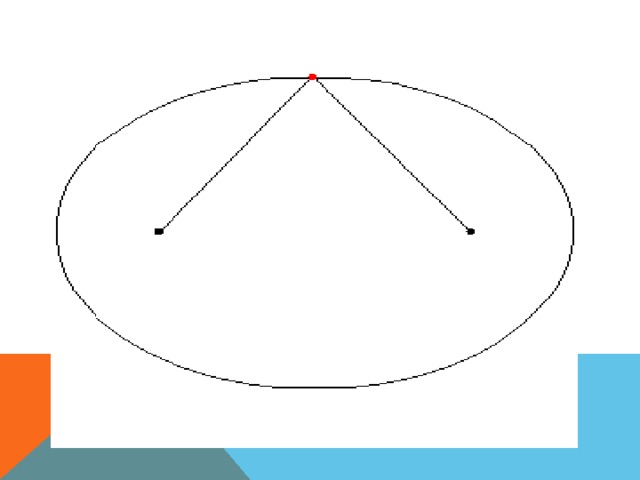

Практика: н а картоне поставьте две точки (фокусы) и протяните через них нитку. Натяните нитку карандашом и нарисуйте фигуру.
Исследование: что произойдет, если
1 ряд фокусы приблизить друг к другу;
2 ряд фокусы удалить друг от друга;
3 ряд фокусы совместить?

Итог и выводы : каким свойством обладают все точки эллипса (вспомните как мы строили эту кривую).
Итак, сумма расстояний от любой точки эллипса до двух точек плоскости (фокусов) есть величина постоянная. Окружность частный случай эллипса.
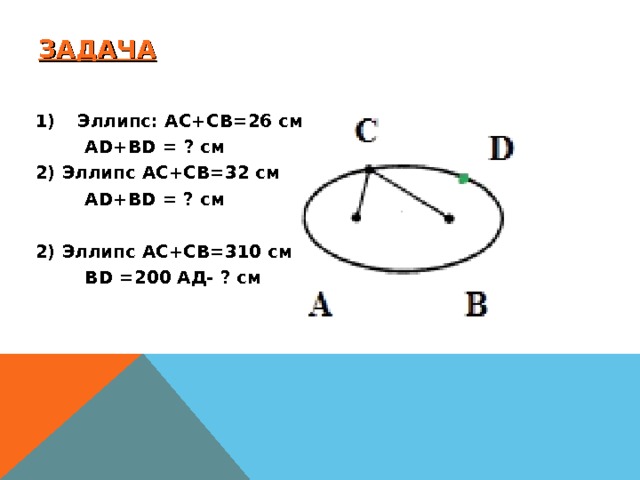
2) Эллипс АС+СВ=32 см
2) Эллипс АС+СВ=310 см

О, ЭЛЛИПС (ИЗ ИСТОРИИ)



Закономерные кривые линии
Познакомимся ещё с несколькими закономерными кривыми линиями.
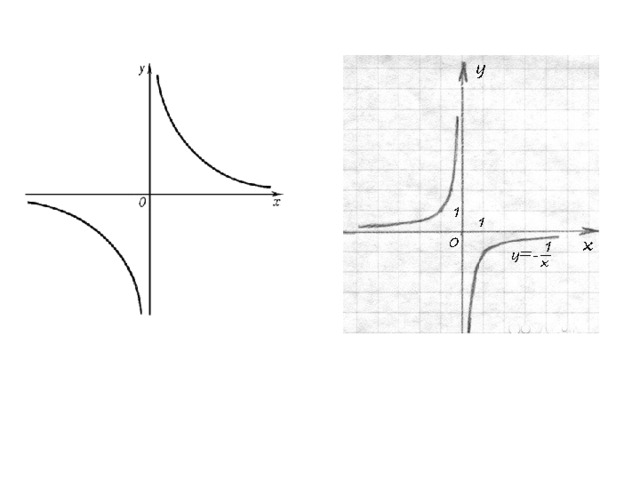
Эта кривая, так же как и эллипс, имеет два фокуса, но в отличие от эллипса, гипербола состоит из двух отдельных ветвей. Основное свойство гиперболы: разность расстояний от любой точки гиперболы до двух её фокусов является постоянной величиной.

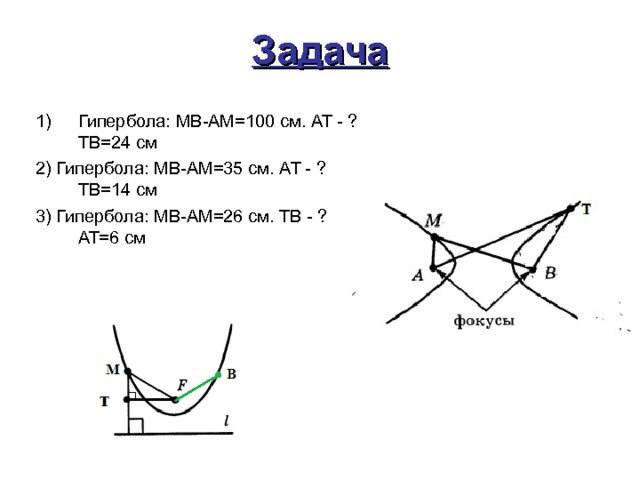
2) Гипербола: MB-AM=35 см. АТ - ? ТВ=14 см
3) Гипербола: MB-AM= 26 см. ТВ - ? АТ=6 см

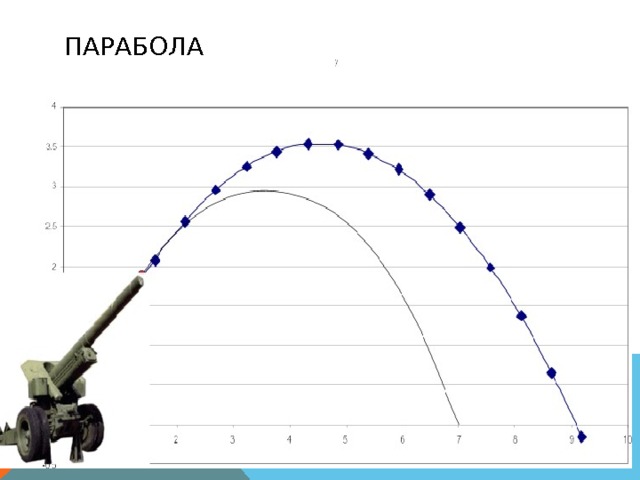
Эту замечательную кривую можно встретить в повседневной жизни. Например камень, брошенный под углом к поверхности Земли, или стрела, пущенная из лука также под углом к земле, двигаются по параболе. Траектории полёта тел изучались с древних времён в военных целях: было замечено, что снаряды летят по одинаковым кривым, а их вид меняется в зависимости от угла выстрела и начальной скорости.



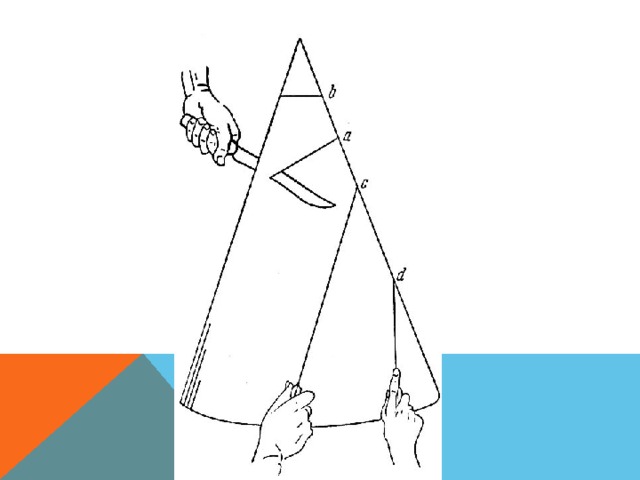

1) Представьте, что конус разрезается плоскостью, параллельной основанию. Какая получится фигура на плоскости разреза (в сечении)?
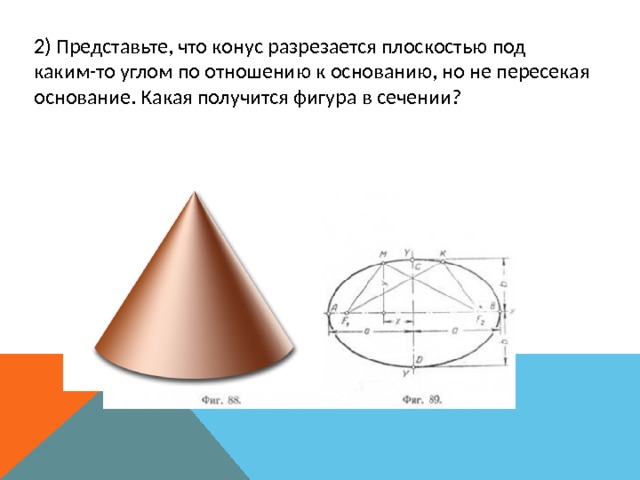
2) Представьте, что конус разрезается плоскостью под каким-то углом по отношению к основанию, но не пересекая основание. Какая получится фигура в сечении?

3) Представьте, что конус разрезается плоскостью, проходящей через боковую поверхность и основание. Какая получится фигура в сечении?
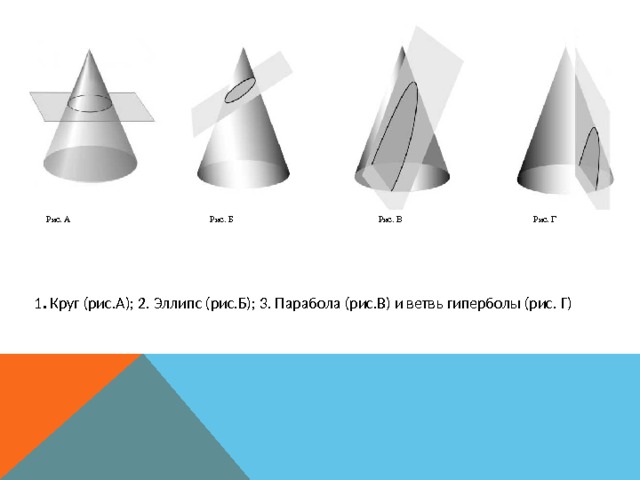
1 . Круг (рис.А); 2. Эллипс (рис.Б); 3. Парабола (рис.В) и ветвь гиперболы (рис. Г)
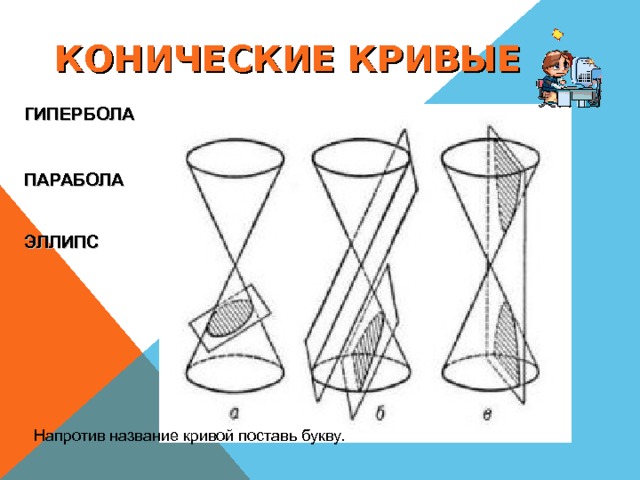
КОНИЧЕСКИЕ КРИВЫЕ
Напротив название кривой поставь букву.

СПИРАЛЬ АРХИМЕДА
Спираль Архимеда
Нарисовать её на глиняном кувшине древнему художнику было не очень сложно: достаточно было вращать гончарный круг и одновременно смещать кисть в фиксированном направлении от центра к краю с постоянной скоростью.

Спираль Архимеда

Спираль Архимеда

Паук плетёт паутину по спирали.
Головка подсолнуха состоит из спиралей Архимеда, одни из которых закручены по часовой стрелке, другие - против.

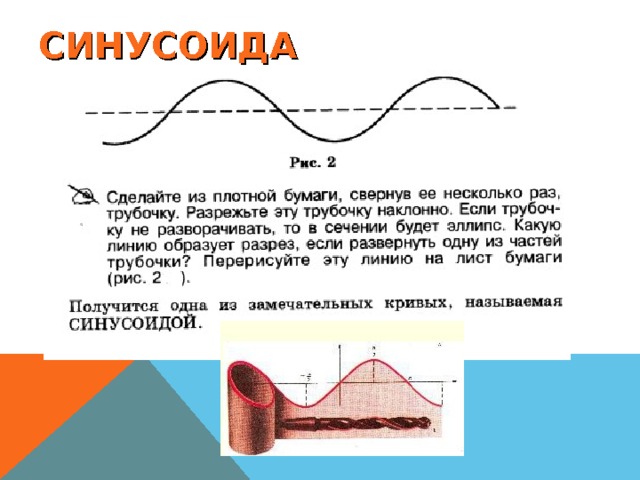
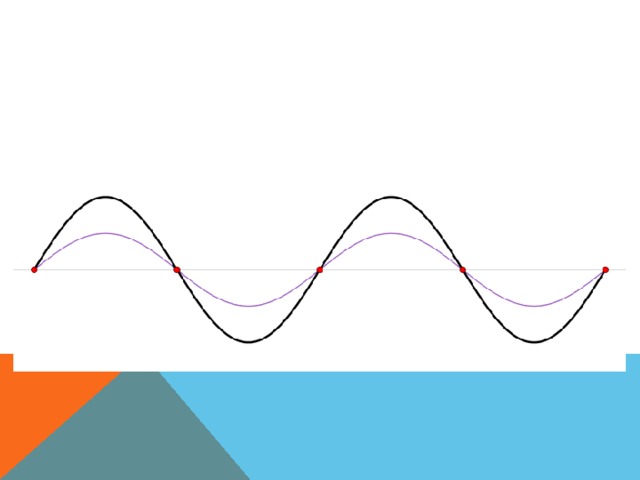

МЫ все живем в пределах синусоиды.
То на плаву, то утопая.
Границы для падения и взлета.
Жизнь – синусоида. Не обессудь.
То, чем один заканчивает путь,
Другому служит точкою отсчета.


Практика (на компьютере):

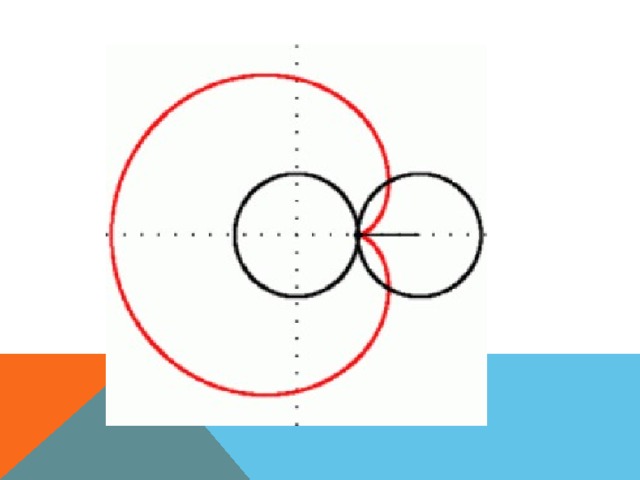
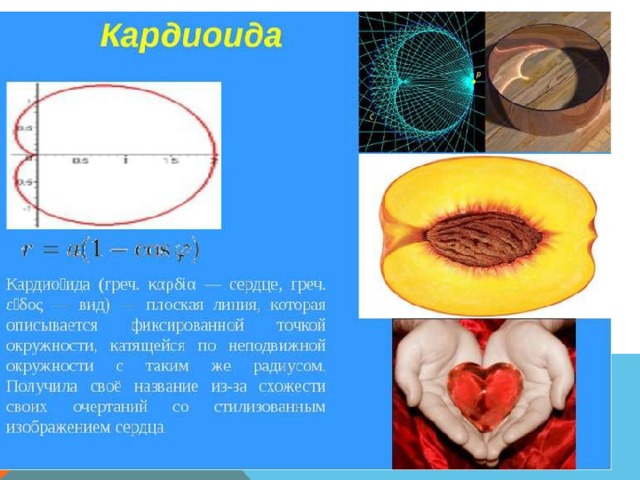

ЭТО КАРДИОИДА. ТАКОЕ НАЗВАНИЕ ОНА ПОЛУЧИЛА ИЗ-ЗА СХЕМАТИЧНОГО СХОДСТВА С СЕРДЦЕМ (ПО ГРЕЧЕСКИ ΚΑΡΔΊΑ — СЕРДЦЕ, ΕἶΔΟΣ — ВИД). НАЗВАНИЕ ПРИДУМАЛ ИТАЛЬЯНСКИЙ МАТЕМАТИК ДЖОВАННИ КАСТИЛЬОНИ (1708 – 1791).
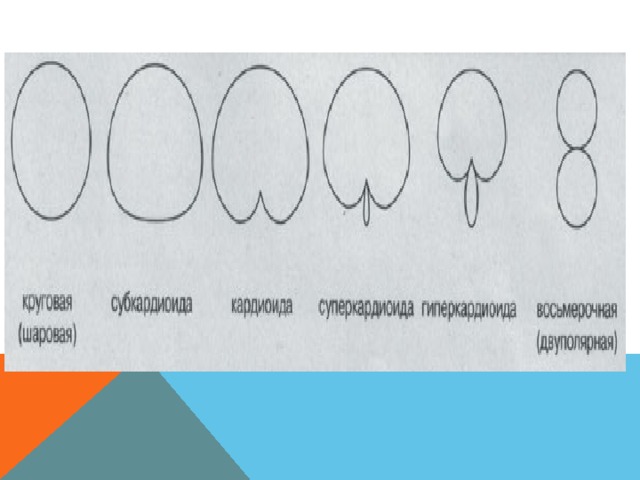

Практика (в Википедии компьютерная модель) :


- Итальянский ученый Галилео Галилей (16-17 в.в.) : желоб выгнуть по дуге окружности.
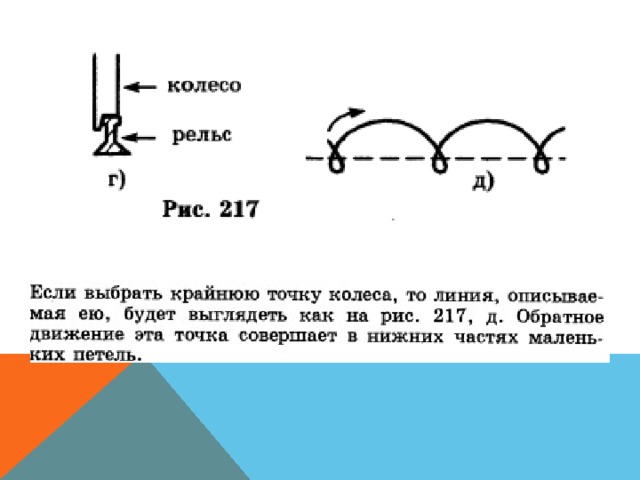
- Швейцарский ученый Иоганн Бернулли (1696 г.) установил, что желоб должен быть выгнут по циклоиде, опрокинутой вниз (рис. 217, в)

КАК ДВИЖУТСЯ КОЛЕСА ПОЕЗДА?

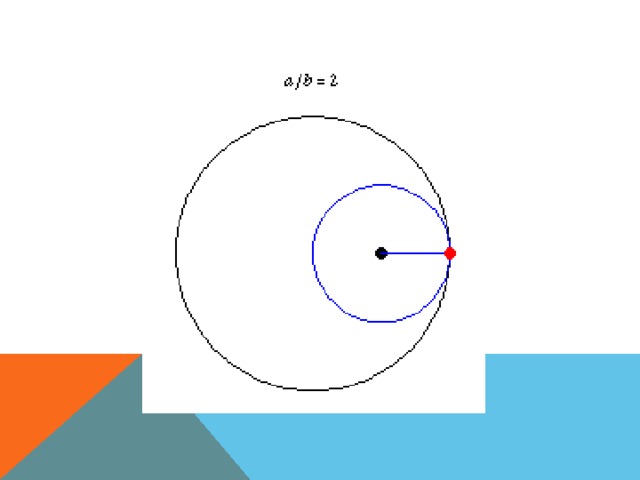
ГИПОЦИКЛОИДА …
Практика (демонстрация на доске или в энциклопедии):


ГИПОЦИКЛОИДА?
Исследование:
Итоги исследования: ________________________________________________________________________________________________________________________________________________________________________________________________

Передо мной овал пруда, Я – с удочкой, рыбачу! Овал похож чуть-чуть на круг, А чем? Реши задачу!
В кардиоиде круг за кругом, Друг за другом И около друга Две души, две спирали бегут. Там и тут, все бегут и бегут.

В этом видеоуроке мы познакомимся с линией, которую называют эллипсом. Рассмотрим частный случай эллипса. Также познакомимся с такими линиями, как гипербола и парабола. Поговорим о конусе. Узнаем, какую кривую называют спиралью Архимеда. Выясним, какие кривые называют синусоидой, кардиоидой, циклоидой. Узнаем, какие линии называют гипоциклоидами.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Замечательные кривые"
Давайте с вами возьмём плотный лист бумаги, прикрепим к нему в двух точках нитку и натянем карандашом эту нитку. Теперь, двигая карандаш и натягивая нитку, нарисуем линию.

Линия, которая у нас получилась, называется эллипсом. Заданные две точки называются фокусами эллипса.

Обратите внимание, что все точки эллипса обладают следующим свойством: сумма расстояний от любой точки эллипса до его фокусов постоянна.
Эллипсы в нашей жизни встречаются гораздо чаще, чем кажется. Так, например, когда мы режем наискосок колбасу, то получающееся сечение имеет эллиптическую форму. Планеты движутся вокруг Солнца по эллиптическим орбитам, причём Солнце находится в одном из фокусов. В архитектуре встречаются элементы, которые напоминают нам эллипс.
Окружность – частный случай эллипса, она получается, если фокусы эллипса совпадают.
На одном из предыдущих занятий мы говорили об окружности и её элементах. Мы научились её строить с помощью циркуля.

Познакомимся со следующей замечательной кривой – гиперболой.

Для этой кривой мы не можем предложить, как в предыдущем случае, достаточно простой способ, позволяющий вычертить гиперболу и одновременно показывающий её основное свойство. Поэтому сразу сформулируем основное свойство, задающее гиперболу.
Гипербола – это линия, для всех точек которой разность расстояний до двух заданных точек плоскости (фокусов гиперболы) есть величина постоянная.


То есть можем записать следующее равенство: .
Вы обратили внимание, что гипербола состоит из двух частей (двух отдельных ветвей). Все точки одной ветви ближе к одному фокусу (соответствующим образом берётся и разность расстояний), а другой ветви к другому фокусу.

Теперь познакомимся с параболой. Возьмём на плоскости прямую l и точку F. Затем отметим на плоскости точку М, которая равноудалена от точки F и от прямой l. Расстояние от точки до прямой – это длина перпендикуляра, проведённого из этой точки к данной прямой. Тогда можем записать, что .
Такие точки (равноудалённые от точки F и от прямой l) описывают замечательную кривую, которая называется параболой.

Эта замечательная кривая не так уж редка в природе. Камень, брошенный человеком под углом к поверхности Земли, описывает параболу.
Ну а теперь поговорим о конусе. Наверное, каждый из вас представляет, что такое конус. Крыши башен часто имеют форму конуса. Архитекторы часто используют такие формы для создания эффекта устремлённости здания вверх.
Конус состоит из двух частей (пол), имеющих общую вершину. Из листа бумаги можно свернуть одну часть.

Математики определяют конус следующим образом. Итак, возьмём окружность и точку над её центром. Эта точка – вершина конуса. Проводя прямые, соединяющие всевозможные точки окружности с вершиной, получим коническую поверхность.

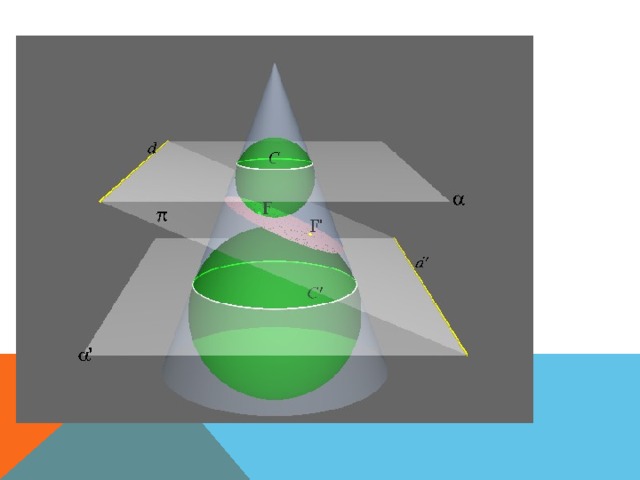
Конус можно пересечь плоскостью по окружности. А вот если плоскость сечения наклонять, то получим эллипс. И чем больше мы будем наклонять плоскость сечения, тем всё более вытянутые эллипсы будут получаться.



Итак, можем сделать вывод, что все рассмотренные выше линии (эллипс, гипербола и парабола) объединяются общим свойством. Каждая из них может быть получена при пересечении конуса плоскостью. Поэтому их называют коническими сечениями.
Сейчас давайте посмотрим на равномерно вращающийся диск, по радиусу которого ползёт муравей. Проползая вперёд, он одновременно смещается в сторону вращения диска.


В природе спираль Архимеда встречается на каждом шагу.
Теперь сделаем из плотной бумаги, свернув её несколько раз, трубочку. Разрежем эту трубочку наклонно. Если трубочку не разворачивать, то в сечении будет эллипс.

А вот если трубочку развернуть, то посмотрите, какую линию образует разрез.

Перерисуем эту линию… Это одна из замечательных кривых, которую называют синусоидой.

Далее вырежем из картона два одинаковых круга. Один из них закрепим неподвижно. Второй круг приложим к первому и отметим на его краю точку, которая наиболее удалена от центра первого круга. Теперь прокатим без скольжения подвижный круг по неподвижному. Обратите внимание, какую линию описала точка.

Начертим эту линию.

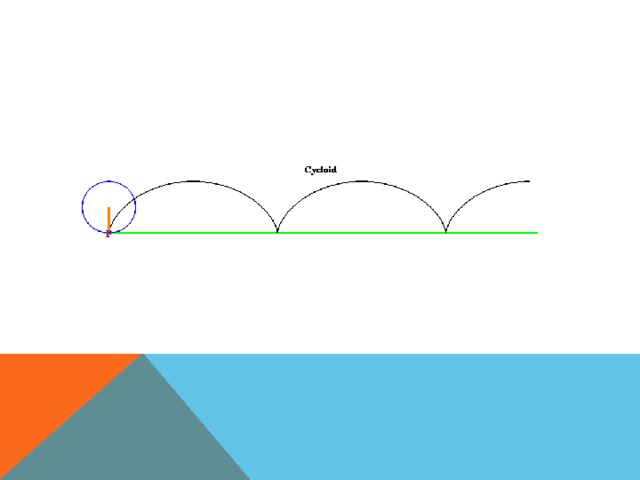
Теперь представим, что по прямой линии без скольжения катится круг, на границе окружности которого взята точка. Посмотрите на траекторию, которую опишет при этом точка. Получившаяся кривая называется циклоидой.

Циклоида обладает многими замечательными свойствами. Вот, например, одно из них. Давно математики пытались решить вот такую задачу: какой формы должен быть гладкий жёлоб, соединяющий две точки – А и B (А выше, чем B), чтобы гладкий металлический шарик скатился по этому жёлобу из точки А в точку B под действием своего веса за кратчайшее время?
Можно подумать, что жёлоб должен быть прямолинейным. Но это не так.
Может быть, жёлоб нужно выгнуть по дуге окружности? Так же думал и великий итальянский физик, астроном и математик Галилео Галилей, живший на рубеже 16-17 веков, но он ошибался.
Иоганн Бернулли – швейцарский математик, механик, врач и филолог-классицист – в одна тысяча шестьсот девяноста шестом году установил, что жёлоб должен быть выгнут по циклоиде, опрокинутой вниз.
Получается, что, скатываясь на санях по снежной горке, форма которой близка к опрокинутой циклоиде, мы окажемся у основания этой горки быстрее, чем в случае другой формы горки.

Сейчас возьмём кусок толстого картона и вырежем в нём круг радиусом 12 см. Из такого же картона вырежем три круга радиусами 4 см, 3 см и 2 см.
Далее вложим в круглое отверстие в картоне круг радиусом 4 см, чтобы он касался края. При этом на окружности этого круга отметим точку А.

Проследим за тем, какую линию опишет отмеченная точка А, когда кружок покатится по окружности выреза без скольжения. Посмотрите, какая линия получилась…

Проделаем то же самое с кругом с радиусом 3 см. Посмотрите, какую линию при этом описала точка А…

И проделаем то же самое ещё раз, но с кругом с радиусом 2 сантиметра. Посмотрите, какую линию описала точка А сейчас…
Читайте также:

