Какие операции определены в множестве рациональных чисел кратко

Обновлено: 15.07.2024

При изложении курса математического анализа для сокращения будем использовать логические символы ∀, ∃, ⇒ ⇔, значения которых приводятся ниже.

∀ — знак общности. Заменяет собой слова: для любого, для каждого, для всех.

∃ — знак существования. Заменяет собой слова: существует, найдется.

⇒ — знак следования (импликации). Запись A ⇒ B означает, что A влечет B или B следует из A.

⇔ — знак равносильности (эквивалентности). Запись A ⇔ B означает, что B следует из A и A следует из B. Иначе: A равносильно B, A необходимо и достаточно для B; A тогда и только тогда, когда B.

Символы ∀, ∃ называются кванторами (общности и существования).

Кроме указанных символов, употребляются также следующие знаки:

Докажем, что A ⇒ B, A ⇔ C.

Предположим, что из A не следует B. Тогда D = b 2 — 4ac ≥ 0. В этом случае квадратный трехчлен y = ax 2 + bx + c имеет действительные корни x₁ и x₂ (x₁ = x₂ при D = 0) и поэтому обращается в нуль при x = x₁ и при x = x₂, что противоречит A. Итак, предположение о том, что из А не следует B, является неверным. Поэтому из A следует B, то есть A ⇒ B.
Докажем, что A ⇔ C. Воспользуемся равенством$$y=a\left[\left(x+\frac b\right)^2+\frac\right]\label$$Так как A ⇒ < D 0следует, что a > 0. Итак, A ⇒ C.Обратно, если имеет место C, то есть D 0, то из равенства \eqref следует, что y > 0 при всех x.Таким образом, квадратный трехчлен y = ax 2 + bx + c принимает положительные значения при всех действительных значениях x тогда и только тогда, когда a > 0 и D = b 2 — 4ac Пример 2.

Пусть заданы числовое множество X и число M. Записать с помощью кванторов отрицание утверждений:

Пусть A не имеет места, то есть не все элементы x множества X удовлетворяют условию x 0 такого, чтобы для любого x ∈ X имело место неравенство |x| ≥ M. Это означает, что для любого M > 0 неравенство |x| ≥ M не может выполняться для каждого x ∈ X. Иначе говоря, существует такой элемент x = x_M ∈ X (зависящий, вообще говоря, от M), для которого неравенство |x| ≥ M не выполняется, то есть справедливо неравенство |x| 0; \ \forall x \ \in \ X \ \rightarrow \ \left|x\right| \ \geq \ M\right\>\nonumber$$

$$\rceil B=\left\ 0; \ \exists x_M \ \in \ X \ \rightarrow \ \left|x_M\right|

Рациональные числа и их свойства.

Рациональное число — такое число, которое можно записать в виде p/q, где p — целое число, q — натуральное число. В частности, любое целое число является рациональным, поскольку его можно записать в виде p = p/1. Например, 0 = 0/1, 1=1/1.

Пусть a = p/q, b = p₁/q₁ — два рациональных числа. Тогда правило упорядочения этих чисел определяется так:

если pq₁ = qp₁, то a = b;

если pq₁ > qp₁, то a > b;

если pq₁ b и b > c, то a > c (транзитивность);

если a > b, то a + c > b +c при любом c;

если a > b и c > d, то a + c > b + d;

если a > b и c > 0, то ac > bc;

если a > b и c 2 =a, где $a\in\mathbb$, не всегда разрешимы в множестве $\mathbb$. Так например, уравнение x 2 =3 не имеет решений в множестве рациональных чисел $\mathbb$.

Докажем, что решение данного уравнения $\sqrt$ не является рациональным числом.

Тогда p 2 можно записать так:

$$
p^2=p_0^\cdot p_1^\cdot\ldots\cdot p_n^\nonumber
$$
Поскольку p 2 делится на 3 целиком, то это значит, что в нашем разложении какое-то p_i = 3. А поскольку множество всех p_i (i лежит в пределах от 0 до n включительно) образует множество всех делителей исходного p, то 3 также является делителем p. То есть мы можем записать, что:
$$
p=3\cdot k,\qquad k\in\mathbb\nonumber
$$
То есть, если вернемся к одному из первых утверждений и заменим наше p, то получим:
$$
9\cdot k^2=3\cdot q^2\quad\Leftrightarrow\quad q^2=3\cdot k^2\nonumber
$$
Повторяя вышеизложенные рассуждения, получим, что q так же делится на 3, как и p. Предположим, что:
$$
q=3\cdot m,\qquad m\in\mathbb\nonumber
$$
Таким образом:
$$
\frac
=\frac=\frac,\nonumber
$$
что противоречит первоначальному утверждению, что p/q — несократимая дробь. Следовательно, $\sqrt$ не является рациональным. $\bullet$

Таким образом, уже проблема решения простых уравнений типа x 2 =a, x 3 =a, где $a\in\mathbb$, приводит к необходимости расширения множества рациональных чисел $\mathbb$ путем добавления к этому множеству новых элементов, называемых иррациональными числами.

Бесконечные десятичные дроби и их приближения.

Периодичные десятичные дроби.

Известно, что любое рациональное число можно представить либо в виде конечной, либо в виде бесконечной периодической дроби. Например, рациональному числу 5/8 соответствует конечная десятичная дробь 0,625, то есть 5/8=0,625. Аналогично, рациональному числу −27/11 соответствует бесконечная периодическая десятичная дробь −2,454545… = −2(45), то есть −27/11 = −2(45).

Обратно: зная бесконечную периодическую десятичную дробь, можно найти рациональное число, представлением которого эта дробь является. Для этого используют формулу суммы бесконечно убывающей геометрической прогрессии \(a+aq+aq^2+…=\frac a, \ \left|q\right|

Сравнение вещественных чисел.

Сравнение неотрицательных чисел.

Два неотрицательных вещественных числа

называют равными и пишут α = β при k = 0,1,2,…, то есть

Дадим определение α β. Говорят, что число α меньше числа β и пишут α \beta\right\> \ \Leftrightarrow \ \left\ b_0\right\>\vee\left\: \ a_k=b_k, \ k=\overline; \ a_n > b_n\right\>.\nonumber$$

Из определения равенства α = β и неравенств α β следует, что для любых неотрицательных вещественных чисел α и β выполняется одно из трех условий: α = β, α β.

Отметим, что для любого неотрицательного вещественного числа α справедливо неравенство α ≥ 0.

Сравнение произвольных вещественных чисел.

Назовем модулем вещественного числа α вещественное число, обозначаемое символом |α|, представимое той же бесконечной дробью, что и α, но взятое со знаком +. Таким образом, если

$$\alpha=\pm a_0,a_1a_2…a_n…,\qquad то\qquad\left|\alpha\right|=a_0,a_1a_2…a_n…,\nonumber$$

откуда следует, что |α| — неотрицательное вещественное число при любом α.

Введем правило сравнения двух вещественных чисел α и β для случая, когда хотя бы одно из этих чисел отрицательно.

Если α — неотрицательное, β — отрицательное число, то считают, что α > β.

Если оба числа α и β отрицательны, то будем считать, что:

Легко убедиться в том, что сформулированное правило сравнения вещественных чисел в применении к рациональным числам, записанным в виде бесконечных десятичных дробей, приводит к тому же результату, что и правило сравнения рациональных чисел (п.2), представленных в виде отношения целых чисел.

Если $\underline_n$, $\underline_n$ — n-е приближение с недостатком, а $<\overline\alpha>_n$, $<\overline\beta>_n$ — n-е приближение с избытком чисел α и β соответственно, то из правила сравнения вещественных чисел следует, что:

$\underline_n\leq\alpha\leq<\overline\alpha>_n, \ \underline_n\leq\beta\leqslant<\overline\beta>_n$ для любого n ∈ $\mathbb$;

$\alpha

Свойства вещественных чисел, связанные с неравенствами.

Если α и β — вещественные числа, причем α Доказательство.

а) Пусть α и β — рациональные числа (α ∈ \(\mathbb$, β ∈ $\mathbb$). Тогда для них определены арифметические операции, и в качестве r можно взять число $\frac2$, так как

$$\alpha α и α ≥ 0, то β > 0. Пусть

Пусть p — наименьший номер, при котором нарушается равенство a_k = b_k (k=0,1,2,…). Будем считать, что p > 0. Тогда

$$a_0=b_0,\qquad…,\qquad a_=b_,\qquad a_p 0\label$$

Покажем, что рациональное число r = a₀,a₁…a_p-1b_p…b_p+m-1(0) удовлетворяет условию \eqref. Из \eqref следует, что α Следствие.

Если α ∈ $\mathbb$, β ∈ $\mathbb$ и α Лемма 2.

Пусть δ ∈ $\mathbb$, δ’ ∈ $\mathbb$ и пусть существуют такие последовательности рациональных чисел x_n> и y_n>, что для всех n ∈ $\mathbb$ справедливы неравенства$$x_n \ \leq \ \delta \ \leq \ \delta^, \ \leq \ y_n,\label$$

Доказательство.

$\circ$ Пусть равенство \eqref не выполняется; тогда из условия \eqref следует, что δ 0, и поэтому

$$\exists m\in\mathbb: \ \ \ \ \ r^,-r > \frac1.\label$$

Из \eqref и \eqref следует, что

$$x_n \ \leqslant \ \delta

Геометрическая интерпретация вещественных чисел.

Рассмотрим прямую l, выберем на ней начало отсчета (точку O) и масштабный отрезок OE длины 1. Числу 0 поставим в соответствие точку O, числу 1 — точку E, числу -1 — точку E’, симметричную точке E относительно точки O. Положительному числу α =a₀,a₁a₂…a_n… поставим в соответствие точку M, находящуюся справа от O на расстоянии α, а отрицательному числу β = b₀,b₁b₂…b_n… — точку M’, находящуюся слева от O на расстоянии |β|.

Эта прямая называется числовой прямой или числовой осью. Из аксиом геометрии и свойств вещественных чисел следует, что между множеством вещественных чисел $\mathbb$ и числовой прямой l устанавливается взаимно однозначное соответствие: каждому вещественному числу соответствует единственная точка числовой прямой и, наоборот, каждой точке числовой прямой соответствует некоторое вещественное число. Поэтому будем в дальнейшем будем отождествлять множество $\mathbb$ с множеством точек числовой прямой, а вещественные числа часто будем называть точками.

Условимся о следующих обозначениях для некоторых наиболее употребительных числовых множеств:

О чем эта статья:

6 класс, 8 класс

Определение рациональных чисел

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.

Рациональные числа — это те, которые можно представить в виде

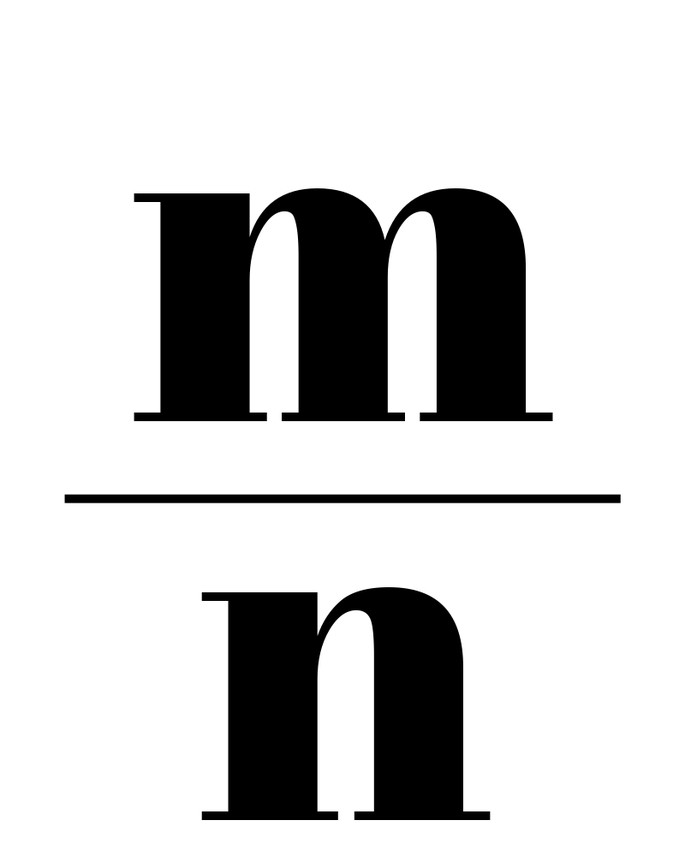
где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

десятичная дробь 1,15 — это 115/100;

десятичная дробь 0,5 — это 1/2;

целое число 0 — это 0/1;

целое число 6 — это 6/1;

целое число 1 — это 1/1;

бесконечная периодическая дробь 0,33333. — это 1/3;

смешанное число — это 25/10;

отрицательная десятичная дробь -3,16 — это -316/100.

Свойства рациональных чисел

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Переместительное свойство сложения: a + b = b + a.

Сочетательное свойство сложения: (a + b) +c = a + (b + c).

Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a.

У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0.

Переместительное свойство умножения: ab = ba.

Сочетательное свойство умножения: (a * b) * c = a * (b * c).

Произведение рационального числа и едины не изменяет это число: a * 1 = a.

У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1.

Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.

Кроме основных перечисленных есть еще ряд свойств:

Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).

Распределительный закон позволяет переписать выражение:

a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d + (-ad).

Мы перечислили только свойства сложения и умножения. На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a - b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Определение иррационального числа

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби

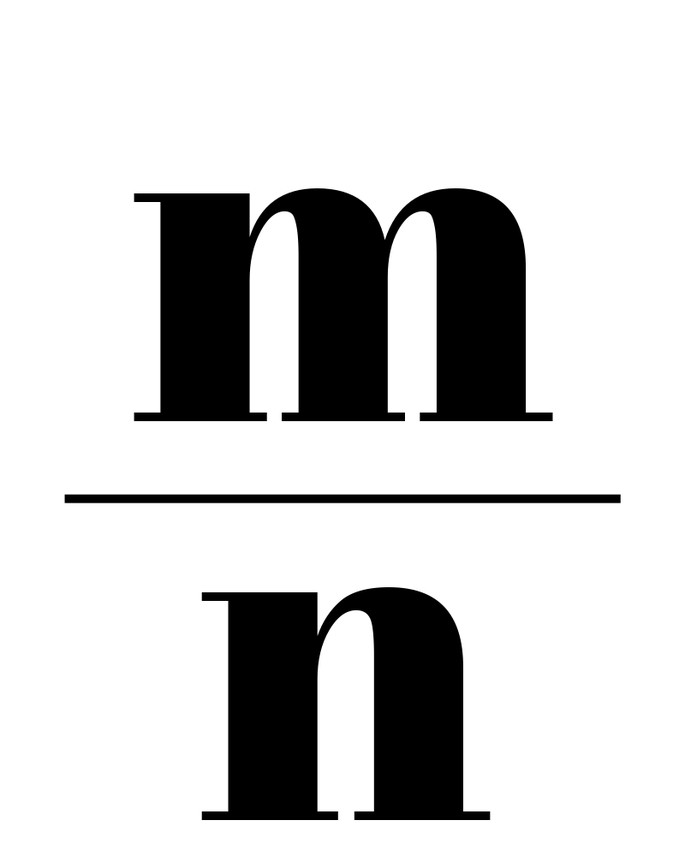
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

π = 3,1415926.

√2 = 1,41421356.

e = 2,71828182…

√8 = 2.828427.

-√11= -3.31662…

Обозначение множества иррациональных чисел: латинская буква I.

Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Свойства иррациональных чисел:

результат суммы иррационального числа и рационального равен иррациональному числу;

результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;

результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;

результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Различие между целыми, натуральными и рациональными числами

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.

А вот, что точно не является натуральным числом:

Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.

Отрицательные числа: -1, -2, -3, -4.

Дроби: 1/2, 3/4, 5/6.

Целые числа — это натуральные числа, противоположные им и нуль.

Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.

Рациональные числа — это конечные дроби и бесконечные периодические дроби.

Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.

Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.

Рациональные числа в математике — какие так называются

Рациональные числа — числа, которые можно представить в виде обычной дроби вида $\frac mn$ , где числитель m — это целое число, а знаменатель n — натуральное.

К рациональным относят целые и дробные числа с положительным или отрицательным знаком, а также ноль. Например, 2, 0, -8, $\frac47, 0,36.$

Множество рациональных чисел не бесконечно, существуют примеры исключений. Доказательством тому служит множество иррациональных чисел. К примеру, рациональными не считают:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

некоторые корни — например, $\sqrt2$ ;

число Пи, число Эйлера, золотое сечение;

непериодические дроби.

Для чего нужны, какой буквой обозначается

Для обозначения множества рациональных чисел используют букву Q. Это множество можно записать в виде:

Свойства рациональных чисел

Одно из основных свойств рациональных чисел — их замкнутость относительно всех арифметических операций.

Это свойство можно объяснить на примере натуральных чисел: 16+14=30. 30 — это натуральное число, как и его слагаемые. Это значит, что множество натуральных чисел замкнуто относительно операции сложения.

С помощью рациональных чисел можно выполнять любые арифметические операции:

сложение: 3,5+2=5,5;

умножение: $-\frac45\cdot\frac54=-1$ ;

вычитание: 1-7,6=-6,6;

деление: $3:8=\frac38$ .

Таким образом, множество Q замкнуто относительно всех четырех операций.

Список свойств рациональных чисел широк. Его можно сократить до нескольких основных пунктов.

Классификация рациональных чисел, виды с примерами

Выделяют несколько групп рациональных чисел.

Целые числа.

Обыкновенные дроби.

Десятичные дроби:

конечные: после запятой стоит определенное количество цифр — например, 0,6; -4,657;

бесконечные периодические: после запятой стоит бесконечное количество цифр, но одна или несколько из них повторяются. Такие повторяющиеся цифры называют периодом. Их записывают в скобках для краткости: $0,33333\dots=0,\left(3\right).$

Какая разница между целыми, натуральными и рациональными числами

Натуральные числа — это все целые числа, начиная с 1. Их множество обозначают буквой N.

1, 14, 47 относятся к натуральным числам.

Это понятие появилось раньше других. Натуральные числа используют для простого счета существующих в окружающем мире предметов. Ноль, отрицательные и дробные числа не входят в множество N. Оно замкнуто относительно операций сложения и умножения.

Целые числа включают в себя натуральные числа, а также ноль и числа, противоположные натуральным — отрицательные. Их множество обозначают буквой Z.

4, 0, -11 относятся к целым числам.

Исторически целые числа возникли как решение проблемы ограниченности натуральных чисел. С развитием математики стало известно о существовании нуля и отрицательных чисел. Однако множество Z не включает в себя дробные числа. Оно замкнуто относительно всех операций, кроме деления.

Множество рациональных чисел, исходя из определения, является наиболее широким из трех. Оно включает в себя все натуральные и целые числа.

Систему отношений между множествами можно представить в виде кругов Эйлера. Схема представлена ниже.

От латинского слова ratio — отношение, деление, дробь происходит математический термин рациональное число или рациональная дробь.

Рациональное число есть число, представляемое обыкновенной дробью m/n , где m — целое число, а n — натуральное. В рациональной дроби число m называется числителем, а число n — знаменателем. Таким образом, рациональная дробь представляет собой результат деления m на n. В действительности дроби часто используются при подсчете частей целого, но неделимого объекта, а также для приблизительной оценки пространственно-временных отношений протяженных объектов.

Множество рациональных чисел принято обозначать Q . Наиболее точная графическая запись рациональных чисел такова: .

Кстати сказать, что дроби типа 3/4 и 9/12 и входят в множество рациональных чисел как одна дробь. Из этого можно сделать вывод, что множество рациональных чисел — это множество несократимых дробей с целым числителем и натуральным знаменателем: , где GCD (m, n) — наибольший общий делитель чисел m и n . Если он равен единице, то это гарантирует взаимную простоту«числителя и знаменателя, что в свою очередь обуславливает несократимость дроби m/n .

Дробь, у которой модуль числителя меньше модуля знаменателя называется правильной. Дробь, не являющаяся правильной относится к неправильным.

Приведем пример, дроби 3/5, 7/8, и 1/2 — правильные дроби, а дроби 8/3, 9/5 и 2/1 — неправильные дроби.

Кстати сказать, что всякое целое число можно записать в виде неправильной обыкновенной дроби со знаменателем 1.

Целое число и правильная дробь называется смешанной дробью, представляющая собой сумму числа и дроби. К примеру, 2 3/7 = 2 + 3/7 = 14/7 + 3/7 = 17/7 .

Интересно узнать, что в математической литературе такая запись практически не используется в связи с тем, что вид такой дроби очень схож с обозначением произведения целого числа на дробь.

К основным свойствам рациональных чисел относятся следующие:

Кроме основных шестнадцати свойств, присущих рациональным числам существуют и другие, которые могут быть выведены из приведенных свойств. Дополнительных свойств рациональных чисел очень много.

Читайте также:


Почему пушкина интересовала история россии полтавская битва и роль в ней петра 1 кратко

В чем причины поражений армий первой и второй коалиций кратко

Чем определяется размер зарплаты должна ли зарплата находится в зависимости от образования кратко

Концепция организационной деятельности кратко

Что такое кеды кратко