Какие элементы многоугольника вы знаете кратко

Обновлено: 06.07.2024

1. Какая фигура ограничивает многоугольник? — Замкнутая ломаная, звенья которой не пересекаются.

2. Могут ли звенья ломаной, ограничивающей многоугольник, пересекаться? — Нет, не могут.

3. Какие элементы многоугольника вы знаете? — Вершина, сторона, углы многоугольника.

4. Как называют и обозначают многоугольник? — Многоугольники называют и обозначают по его вершинам. Чтобы записать название многоугольника, надо последовательно записать все его вершины.

5. Что называют периметром многоугольника? — Периметр многоугольника — это сумма длин все его сторон.

6. Какие многоугольники называют равными? — Многоугольники называют равными, если они совпадают при наложении.

7. Какие фигуры называют равными? — Фигуры называют равными, если они совпадают при наложении.

Решаем устно

1. Сумму чисел 24 и 18 уменьшите на 33.

(24 + 18) — 33 = 42 — 33 = 9

2. Разность чисел 30 и 14 увеличьте в 3 раза.

(30 — 14) • 3 = 16 • 48

3. Произведение чисел 12 и 5 увеличьте на 19.

(12 • 5) + 19 = 60 + 19 = 79

4. Частное чисел 189 и 9 уменьшите в 7 раз.

(189 : 9) : 7 = 21 : 7 = 3

5. Укажите среди данных отрезков равные, если:

• АВ = 5 см 3 мм = 53 мм = TQ
• CD = 4 м 5 см = 405 см
• РК = 45 см
• EF = 2 дм 8 мм = 20 см 8 мм = 208 мм = MN
• TQ = 53 мм = 5 см 3 мм = АВ
• MN= 208 мм = 20 см 8 мм = 2 дм 8 мм = EF

Ответ: АВ = TQ и EF = MN.

Упражнения

321. Назовите вершины и стороны пятиугольника, изображённого на рисунке 109.

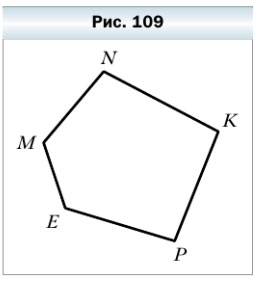
• Вершины пятиугольника: N, K, P, E, M
• Стороны пятиугольника: NK, KP, PE, EM, EN.

322. Начертите: 1) четырёхугольник; 2) пятиугольник; 3) шестиугольник; 4) семиугольник .

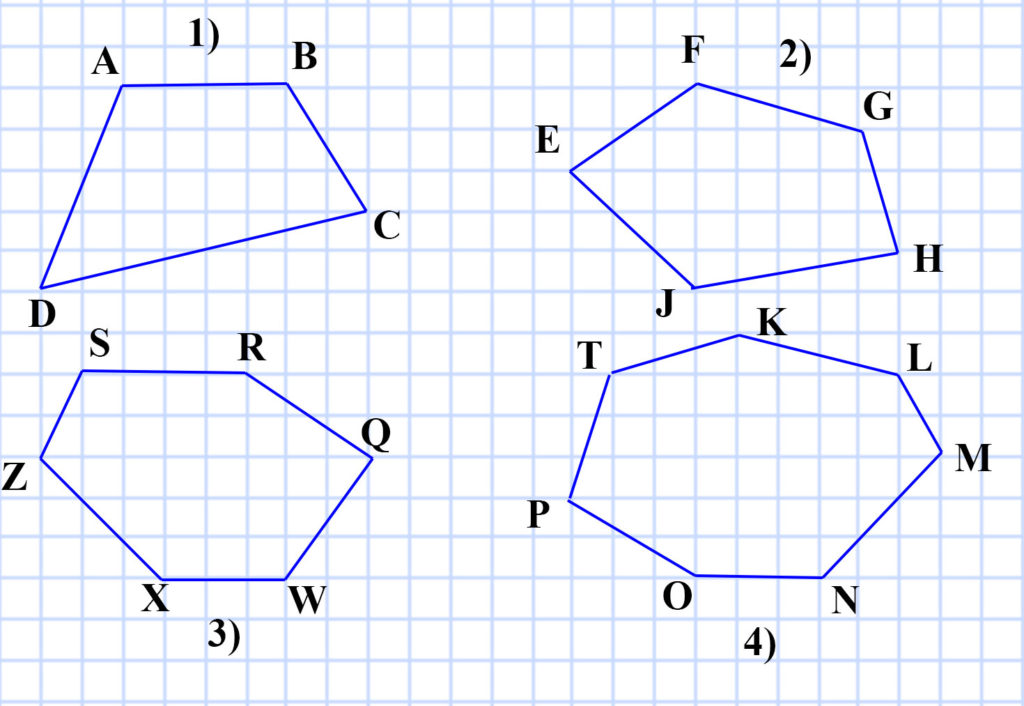
1. Четырехугольник ABCD
2. Пятиугольник EFGHJ
3. Шестиугольник SRQWXZ
4. семиугольник TKLMNOP

323. Вычислите периметр пятиугольника, стороны которого равны 2 см, 4 см, 5 см 5 мм, 6 см, 7 см.

Периметр многоугольника равен сумме длин его сторон.

2 см + 4 см + 5 см 5 мм + 6 см + 7 см = 24 см 5 мм — периметр данного пятиугольника.

Ответ: 24 см 5 мм.

324. Вычислите периметр шестиугольника, три стороны которого равны по 8 см, а три другие — по 10 см.

Периметр многоугольника равен сумме длин его сторон.

8 • 3 + 10 • 3 = 24 + 30 = 54 (см) — периметр данного шестиугольника.

325. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 110.

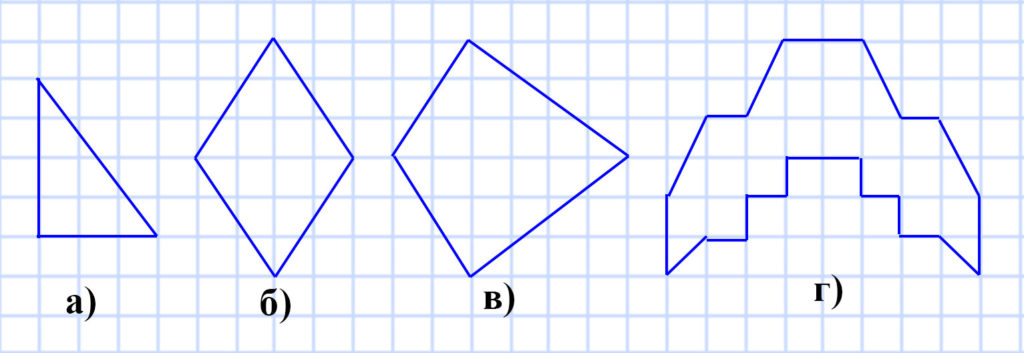
326. Нарисуйте в тетради фигуру, равную той, которая изображена на рисунке 111.

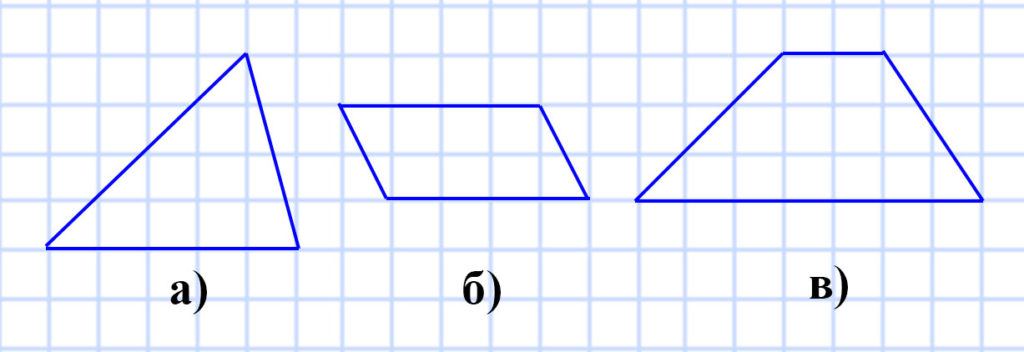
327. Одна из сторон четырёхугольника равна 8 см, вторая сторона в 3 раза больше первой, а третья — на 7 см меньше второй и на 9 см больше четвёртой. Вычислите периметр четырёхугольника.

1) 8 • 3 = 24 (см) — длина второй стороны четырёхугольника.

2) 24 — 7 = 17 (см) — длина третьей стороны четырёхугольника.

3) 17 — 9 = 8 (см) — длина четвёртой стороны четырёхугольника.

4) 8 + 24 + 17 + 8 = 57 (см) — периметр четырёхугольника.

328. Стороны пятиугольника пронумеровали. Первая сторона равна 4 см, а каждая следующая сторона на 2 см длиннее предыдущей. Вычислите периметр пятиугольника.

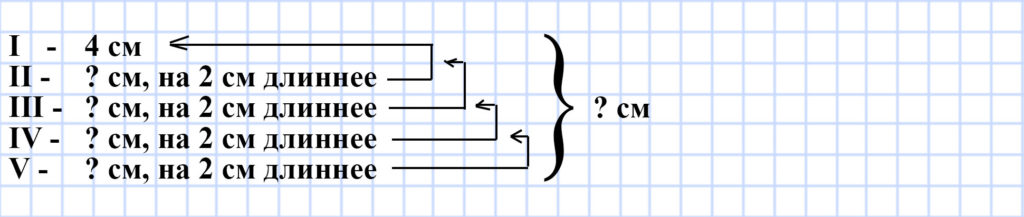
1) 4 + 2 = 6 (см) — длина второй стороны пятиугольника.

2) 6 + 2 = 8 (см) — длина третьей стороны пятиугольника.

3) 8 + 2 = 10 (см) — длина четвёртой стороны пятиугольника.

4) 10 + 2 = 12 (см) — длина пятой стороны пятиугольника.

5) 4 + 6 + 8 + 10 + 12 = 40 (см) — периметр пятиугольника.

329. 1) Сколько диагоналей можно провести из одной вершины: а) пятиугольника; б) девятиугольника; в) и-угольника, где п > 3?

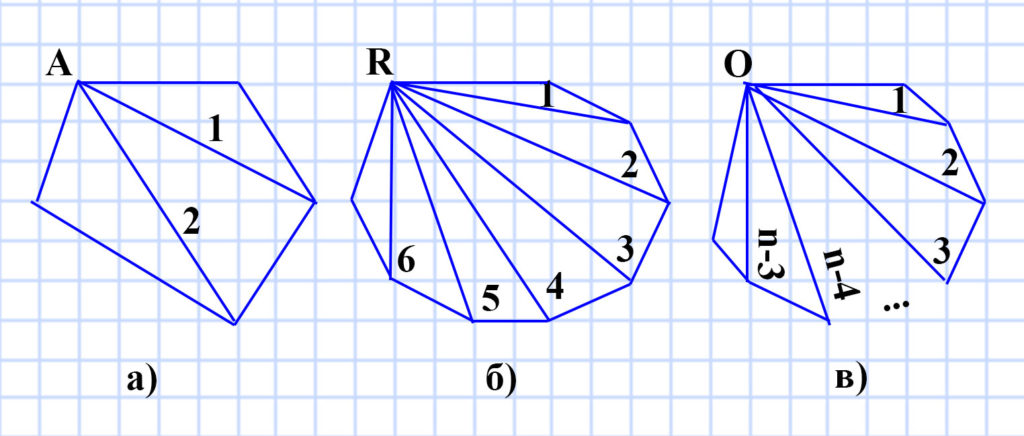
а) Из одной вершины пятиугольника можно провести 2 диагонали.

б) Из одной вершины девятиугольника можно провести 6 диагоналей.

в) Из одной вершины n-угольника можно провести (n-3) диагоналей, так как:

• первая вершина является исходной;
• диагональ ко второй вершине совпадает со одной из сторон, прилегающей к исходной вершине;
• диагональ к последней вершине совпадает с другой из сторон, прилегающей к исходной вершине.

2) Сколько всего диагоналей можно провести: а) в пятиугольнике; б) в девятиугольнике; в) в и-угольнике, где п > 3?

а) Мы знаем, что из одной вершины пятиугольника можно провести 2 диагонали (n-3), Значит из 5 вершин можно провести 5 • 2 = 10 диагоналей (n • (n-3)). Но если провести все 10 диагоналей, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в пятиугольнике можно провести 10 : 2 = 5 диагоналей ((n •(n-3) : 2). Рисунок подтверждает наш вывод.

б) Мы знаем, что из одной вершины девятиугольника можно провести 6 диагоналей (n-3 = 9 — 3 = 6), Значит из 9 вершин можно провести 9 • 6 = 54 диагонали (n • (n-3) = 9 • (9 — 3) = 9 • 6 = 54). Но если провести все 54 диагонали, то каждая пара из них будет совпадать, так как одна диагональ всегда соединяет две вершины. Значит всего в девятиугольнике можно провести 54 : 2 = 27 диагоналей ((n • (n-3) : 2 = 9 • (9 — 3) : 2 = 9 • 6 : 2 = 54 : 2 = 27). Рисунок подтверждает наш вывод.

в) Исследуя предыдущие два задания мы вывели формулу, по которой можно посчитать количество возможных диагоналей в n-угольнике, при n > 3: n • (n-3) : 2. Это значит, у количество диагоналей:

• у четырёхугольника — n • (n-3) : 2 = 4 • (4 — 3) : 2 = 4 • 1 : 2 = 4 : 2 = 2 — верно
• у шестиугольника — n • (n-3) : 2 = 6 • (6 — 3) : 2 = 6 • 3 : 2 = 18 : 2 = 9 — верно
• у семиугольника — n • (n-3) : 2 = 7 • (7 — 3) : 2 = 7 • 4 : 2 = 1=28 : 2 = 14 — верно
• и т.д.

Ответ: 5, 27, n • (n-3) : 2.

330. Как, используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2°?

Для того, чтобы используя шаблон угла, градусная мера которого 13°, построить угол, градусная мера которого равна 2° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла;
2. начиная от одного из лучей развёрнутого угла последовательно 14 раз отложить по шаблону угол в 13°;
3. так как 13° • 14 = 182°, то последний из отложенных по шаблону углов будет на 2° выходить за границы развёрнутого угла;
4. угол, выходящий за границы развёрнутого угла, как раз и будет искомым углом с градусной мерой 2°.

331. Как построить угол, градусная мера которого 1°, используя шаблон угла, градусная мера которого равна:

а) 19°

Для того, чтобы используя шаблон угла, градусная мера которого 19°, построить угол, градусная мера которого равна 1° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла;
2. начиная от одного из лучей развёрнутого угла последовательно 19 раз отложить по шаблону угол в 19°;
3. так как 19° • 19 = 361°, то последний из отложенных по шаблону углов будет на 1° выходить за границы двух развёрнутых углов;
4. угол, выходящий за границы развёрнутых углов, как раз и будет искомым углом с градусной мерой 1°.

б) 7°

Для того, чтобы используя шаблон угла, градусная мера которого 7°, построить угол, градусная мера которого равна 1° надо:

1. прочертить прямую линию и отметить на ней точку вершины развёрнутого угла.
2. провести из этой точки перпендикуляр к прямой;
3. начиная от одного из лучей развёрнутого угла последовательно 13 раз отложить по шаблону угол в 7°;
4. так как 7° • 13 = 91°, то последний из отложенных по шаблону углов будет на 1° выходить за границы прямого угла образованного перпендикуляром к прямой;
5. угол, выходящий за границы прямого угла, как раз и будет искомым углом с градусной мерой 1°.

332. Существует ли многоугольник с периметром, равным 1 000 000 см, который можно целиком расположить в квадрате со стороной 1 см?

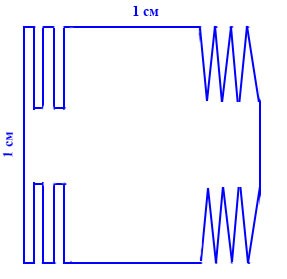
Да, теоретически такой многоугольник существует. Для этого надо из квадрата со стороной 1 см вырезать множество полосок либо треугольников, либо ещё каких-нибудь фигур вдоль нескольких сторон исходного квадрата. Точное количество таких вырезанных фигур будет зависеть от длины вырезаемых из квадрата сторон фигуры, а также от длины оставшихся от исходного квадрата сторон.

В реальности такую операцию способны выполнить только суперточные приборы, например лазерный принтер. Кроме того, необходимо провести очень точный расчёт вырезаемых фигур.

Упражнения для повторения

333. Сравните:

1) 3 986 г и 4 кг: 4 кг = 4000 г ⇒ 3 986 г

2) 6 м и 712 см: 6 м = 600 см ⇒ 600 см

3) 60 см и 602 мм: 60 см = 600 мм ⇒ 600 мм

4) 999 кг и 10 ц: 10 ц = 1000 кг ⇒ 999 кг

334. Выполните сложение, выбирая удобный порядок вычислений:

1) (636 + 927) + 364 = (636 + 364) + 927 = 1 000 + 927 = 1 927

2) (425 + 798) + 675 = (425 + 675) + 798 = 1 100 + 798 = 1 898

3) 212 + 493 + 788 + 807 = (212 + 788) + (493 + 807) = 1 000 + 1 300 = 2 300

4) 161 + 455 + 839 + 945 = (161 + 839) + (455 + 945) = 1 000 + 1 400 = 2 400

335. Известно, что ∠ABC = 74°, а луч BD — его биссектриса. Вычислите величину угла DBC.

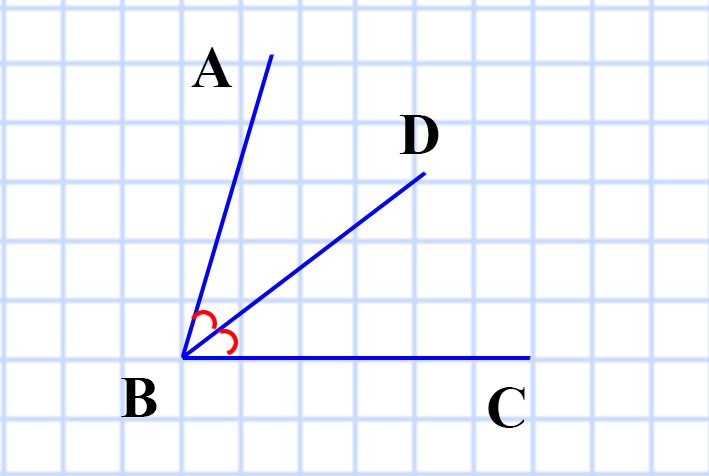
Мы знаем, что биссектриса угла всегда делит угол пополам. Значит:

∠DBC = ∠ABC : 2 = 74° : 2 = 37°

336. Высота самой высокой горы Западной Европы Монблан равна 4 809 м. Она на 2 151 м ниже самой высокой горы Южной Америки Аконкагуа, которая на 770 м выше самой высокой горы Северной Америки Денали. Какова высота самой высокой горы Африки Килиманджаро, если она на 295 м ниже горы Денали? Какова высота самой высокой горы мира Джомолунгмы (Эверест) (рис. 112), если она на 2 953 м выше горы Килиманджаро?

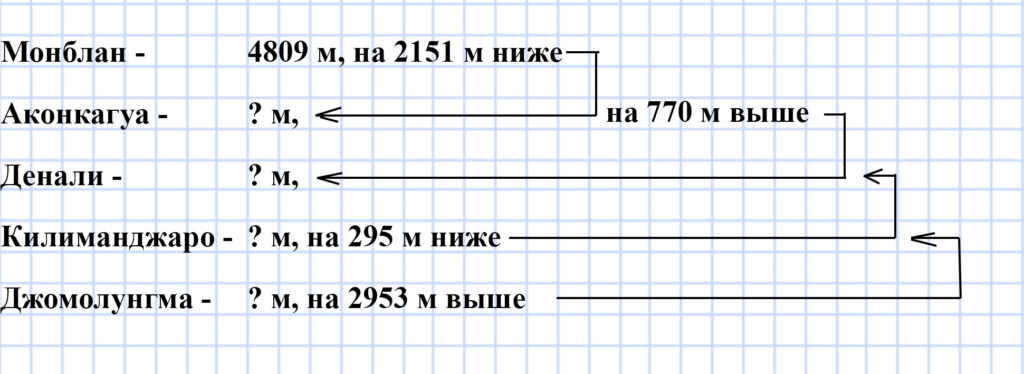
1) 4 809 + 2 151 = 6 960 (м) — высота горы Аконкагуа.

2) 6 960 — 770 = 6 190 (м) — высота горы Денали.

3) 6 190 — 295 = 5 895 (м) — высота горы Килиманджаро.

4) 5 895 + 2 953 = 8 848 (м) — высота горы Джомолунгма.

Ответ: 8 848 метров.

Задача от мудрой совы

337. Лимоны одинаковой массы продают поштучно. Масса каждого лимона составляет целое количество граммов. Купили больше двух, но меньше семи лимонов. Масса всей покупки составляет 850 г. Какова масса одного лимона?

Так как купили больше двух, но меньше семи лимонов, то количество купленных лимонов может быть либо 3, либо 4, либо 5, либо 6.

Масса каждого лимона — целое число, причём все лимоны одинаковые. Проверим, на какое из возможных чисел (3, 4, 5 или 6) общая масса покупки 850 г делится без остатка. Для этого применим метод подбора.

Определение 1. Многоугольник − замкнутая ломаная линия.

Объединение многоугольника и ограниченной им части плоскости также называют многоугольником. Поэтому представим другое определение многоугольника:

Определение 2. Многоугольник − это геометрическая фигура, которая является частю плоскости, ограниченная замкнутой ломаной.

Вершины ломаной называются вершинами многоугольника. Звенья ломаной называются сторонами многоугольника.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней областью многоугольника, а другая внешней областью многоугольника.

Виды многоугольников

Многоугольник с тремя вершинами называется треугольником, с четыремя вершинами − четырехугольником, с пяти вершинами − пятиугольником, и т.д. Многоугольник с \( \small n \) вершинами называется \( \small n- \)угольником.

На рисунке 1 представлены различные виды многоугольников.

Обозначение многоугольника

Обозначают многоугольник буквами, стоящих при его вершинах. Называют многоугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, многоугольник на рисунке 2 называют \( \small A_1A_2A_3A_4A_5A_6 \) или \( \small A_6A_5A_4A_3A_2A_1 \).

Соседние вершины многоугольника

Вершины многоугольника называются соседними, если они являются концами одной из его сторон.

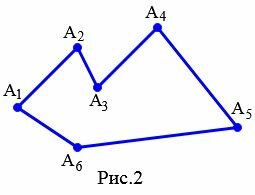На рисунке 2 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)

Смежные стороны многоугольника

Стороны многоугольника называются смежными, если они имеют общую вершину.

На рисунке 2 стороны \( \small A_4A_5 \) и \( \small A_5A_6 \) являются смежными, так как они имеют общую вершину \( \small A_5. \)

Простой многоугольник. Самопересекающийся многоугольник

Многоугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).

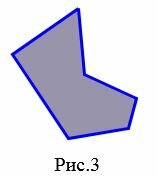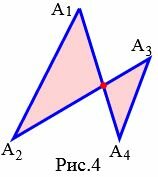На рисунке 3 изображен простой многоугольник так как стороны многоугольника не имеют самопересечений. А на рисунке 4 многоугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой многоугольник называется самопересекающийся многоугольник.

Выпуклый многоугольник

Многоугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.

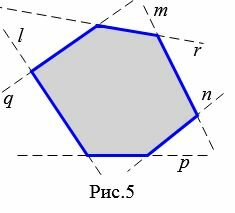На рисунке 5 многоугольник лежит по одну сторону от прямых \( \small m, \ n, \ l, \ p, \ q, \ r\) проходящих через стороны многоугольника.

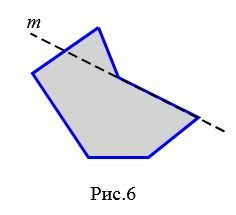На рисунке 6 прямая \( \small m\) делит многоугольник на две части, т.е. многоугольник не лежит по одну сторону от прямой \( \small m\). Следовательно многоугольник не является выпуклым.

Правильный многоугольник

Простой многоугольник называется правильным, если все его стороны равны и все углы равны. Например равносторонний треугольник является правильным многоугольником, поскольку все его стороны равны, и все его углы равны 60°. Квадрат является правильным многоугольником, так как все его стороны равны и все его углы равны 90°.

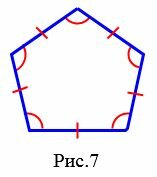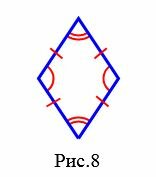На рисунке 7 изображен правильный многоугольник (пятиугольник), так как у данного многоугольника все стороны равны и все углы равны. Многоугольник (ромб) на на рисунке 8 не является правильным, так как все стороны многоугольника равны, но все углы многоугольника не равны друг другу. Прямоугольник также не является правильным многоугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.

Звездчатый многоугольник

Самопересекающийся многоугольник, все стороны которого равны и все углы равны, называется звездчатым или звездчато-правильным.

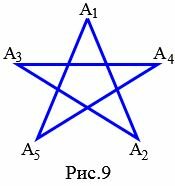На рисунке 9 представлен звездчатый пятиугольник поскольку все углы \( \small A_1, \ A_2, \ A_3, \ A_4, \ A_5 \) равны и равны все стороны: \( \small A_1A_2=A_2A_3=A_3A_4=A_4A_5=A_5A_1. \)

Периметр многоугольника

Сумма всех сторон многоугольника называется периметром многоугольника. Для многоугольника \( \small A_1A_2. A_A_n \) периметр вычисляется из формулы:

Угол многоугольника

Углом (внутренним углом) многоугольника при данной вершине называется угол между двумя сторонами многоугольника, сходящимися к этой вершине. Если многоугольник выпуклый, то все углы многоугольника меньше 180°. Если же многоугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small A_3 \) на рисунке 2).

Внешний угол многоугольника

Внешним углом многоугольника при данной вершине называется угол смежный внутреннему углу многоугольника при данной вершине.

На рисунке 10 угол 1 является внешним углом данного многоугольника при вершине \( \small E. \)

Диагональ многоугольника. Количество диагоналей

Диагоналями называют отрезки, соединяющие две несоседние вершины многоугольника.

Выведем форулу вычисления количества диагоналей многоугольника. Пусть задан \( \small n \)-угольник. Выберем одну вершину многоугольника и проведем мысленно все отрезки, соединяющие эту вершину с остальными вершинами. Получим \( \small n-1 \) отрезков. Но поскольку две вершины для выбранной вершины являются соседними, а по определнию диагональ − это отрезок соединяющий несоседние вершины, то из \( \small n-1 \) вычтем 2. Получим \( \small n-3 \). Всего \( \small n \) вершин. Следовательно количество вычисленных диагоналей будет \( \small n(n-3). \) Учитывая, что каждый диагональ − это отрезок соединяющий две вершины, то получится, что мы вычислили каждый диагональ дважды. Поэтому полученное число нужно делить на два. Получим количество диагоналей \( \small n- \)мерного многоугольника:

Сумма углов выпуклого многоугольника

Выведем формулу вычисления суммы углов выпуклого многоугольника. Для этого проведем из вершины \( \small A_1 \) все диагноали многоугольника \( \small A_1A_2. A_A_n \) (Рис.11):

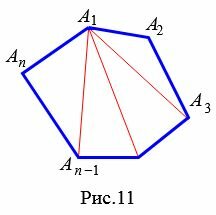Количество диагоналей, проведенной из одной вершиы, как выяснили из предыдующего параграфа равно \( \small n-3 \). Следовательно, эти диагонали разделяют многоугольник на \( \small n-3+1=n-2 \) треугольников. Поскольку сумма углов треугольника равна 180°, то получим, что сумма углов выпуклого многоугольника равна: \( \small 180°(n-2). \)

где \( \small n \) −количество сторон (вершин) выпуклого многоугольника.

Угол правильного многоугольника

Поскольку у правильного многоугольника все углы равны, то используя формулу (1) получим угол правильного многоугольника:

где \( \small n \) −количество сторон (вершин) правильного многоугольника.

Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.

Точки называются вершинами ломаной, а отрезки — звеньями ломаной.

Ломаная называется замкнутой , если у неё концы совпадают.

Если концы ломаной не совпадают, то она называется незамкнутой .

Ломаная называется простой , если она не имеет самопересечений. Обе ломаные выше являются простыми.

Многоугольник — это простая замкнутая ломаная линия и конечная часть

Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.

Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.

Многоугольник, у которого все углы меньше 180 ° , называется выпуклым многоугольником.

Пятиугольник \(ABCDE\) является выпуклым многоугольником.

В общем случае многоугольник можно назвать \(n\)-угольником, это означает, что у данного многоугольника \(n\) сторон и \(n\) вершин.

Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на \(2\) меньше, чем количество сторон в многоугольнике.

Многоугольник — это геометрическая фигура, ограниченная замкнутой ломаной линией, не имеющей самопересечений.

Звенья ломаной называются сторонами многоугольника, а её вершины — вершинами многоугольника.

Углами многоугольника называются внутренние углы, образованные соседними сторонами. Число углов многоугольника равно числу его вершин и сторон.

Многоугольникам даются названия по количеству сторон. Многоугольник с наименьшим количеством сторон называется треугольником, он имеет всего три стороны. Многоугольник с четырьмя сторонами называется четырёхугольником, с пятью — пятиугольником и т. д.

Обозначение многоугольника составляют из букв, стоящих при его вершинах, называя их по порядку (по часовой или против часовой стрелки). Например, говорят или пишут: пятиугольник ABCDE :

В пятиугольнике ABCDE точки A, B, C, D и E — это вершины пятиугольника, а отрезки AB, BC, CD, DE и EA — стороны пятиугольника.

Выпуклые и вогнутые

Многоугольник называется выпуклым, если ни одна из его сторон, продолженная до прямой линии, его не пересекает. В обратном случае многоугольник называется вогнутым:

Периметр

Сумма длин всех сторон многоугольника называется его периметром.

Периметр многоугольника ABCDE равен:

AB + BC + CD + DE + EA.

Если у многоугольника равны все стороны и все углы, то его называют правильным. Правильными многоугольниками могут быть только выпуклые многоугольники.

Диагональ

Диагональ многоугольника — это отрезок, соединяющий вершины двух углов, не имеющих общей стороны. Например, отрезок AD является диагональю:

Единственным многоугольником, который не имеет ни одной диагонали, является треугольник, так как в нём нет углов, не имеющих общих сторон.

Если из какой-нибудь вершины многоугольника провести все возможные диагонали, то они разделят многоугольник на треугольники:

Треугольников будет ровно на два меньше, чем сторон:

t = n - 2,

где t — это количество треугольников, а n — количество сторон.

Разделение многоугольника на треугольники с помощью диагоналей используется для нахождения площади многоугольника, так как чтобы найти площадь какого-нибудь многоугольника, нужно разбить его на треугольники, найти площадь этих треугольников и полученные результаты сложить.

Читайте также:

  
• План урока family and friends 2
  
• Что такое полюс география 5 класс кратко
  
• Почему мише захотелось попасть в табакерку что удивило мальчика когда он ее впервые увидел кратко
  
• Какой должна быть современная девушка кратко
  
• Welcome to disneyland план урока