Какая фигура называется выпуклой кратко

Обновлено: 28.06.2024

Но при решении задач, нельзя опираться на рисунок. Поэтому нужно определение. В школьных учебниках чаще всего используется такое:

Выпуклый многоугольник — это многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две соседние вершины.

То есть, если сторону многоугольника продлить до прямой, то вся фигура должна оказаться по одну сторону от неё. Это условие должно выполняться для каждой стороны.

Таким определением не просто пользоваться. Поэтому я даю детям следующее:

Выпуклый многоугольник — это многоугольник, все диагонали которого лежат внутри многоугольника.

На мой взгляд с его помощью, детям легче увидеть разницу в фигурах.

Недавно объясняя ученику эту тему, столкнулась с тем, что ребенок уловил разницу, но путал определения. То есть он понимал, чем отличается один от другого, но не мог правильно запомнить название. Пришлось прибегнуть к хитрости. Эмоционально окрашенная информация запоминается лучше . Поэтому я рассказала, что не выпуклый многоугольник это комната. Внутри неё находится человек, который наталкивается на угол. После этого человечку становится не хорошо. Ребенок посмеялся и перестал путать названия.

Через несколько часов я вспомнила историю про крокодильчиков, которую мне рассказал коллега.

Интересно, что расскажет мой ученик про выпуклые многоугольники на следующем занятии.

Если отрезок, соединяющий любые две точки фигуры, полностью принадлежит фигуре во всех точках, то фигура выпуклая.

Выпуклой называется такая фигура, которой принадлежат все точки отрезка, соединяющего любые ее две точки. Выпуклыми фигурами являются, например, круг, шар, треугольник; четырехугольники могут быть как выпуклыми, так и невыпуклыми

Выпуклая фигура ПОЛНОСТЬЮ ЛЕЖИТ с одной стороны от прямой, проведенной через любую её сторону. Если фигура "гладкая" (криволинейная, хотя бы частично), то - с одной стороны от любой своей касательной ("касательные" к вершинам НЕ считаются).

Если речь многограннике, то все плоские углы при всех вершинах у выпуклого многогранника будут не более 180 градусов.

Выпуклым называют многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящий через две его соседние вершины.

Или же другой вариант определения:

Выпуклым называют многоугольник, в котором соблюдается следующее условие: если выбрать две произвольных точки, лежащих внутри фигуры, и соединить их отрезком, то все точки этого отрезка так же будут лежать внутри многоугольника.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Примеры

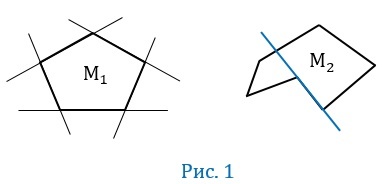
Многоугольник \(М_1\) — выпуклый, а \(М_2\) — не выпуклый.

Сумма углов выпуклого многоугольника

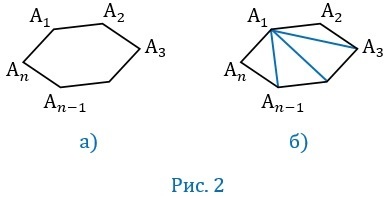
\(A_1A_2A_3. A_n\) — выпуклый многоугольник. Найдем сумму его углов:

\(\angle A_nA_1A_2,\;\angle A_1A_2A_3,\;\angle A_A_nA_1,\;. \)

Соединим вершину \(А_1\) с другими. Эти отрезки называются диагоналями. В таком случае образуется n-2 треугольника. Сумма всех их углов будет такой же, как и сумма углов исходного n-угольника. Сумма углов треугольника равна \(180^\circ\) , тогда сумма углов многоугольника равна \(180^\circ(n-2)\) .

Сумма углов выпуклого n-угольника равна \(180^\circ(n-2)\) .

Сумма внешних углов выпуклого многоугольника

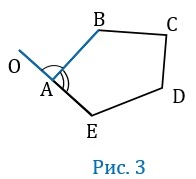
\(\angle OAD\) — внешний угол многоугольника ABCDE при вершине А. (смежный с \(\angle BAE\) )

Возьмем по одному внешнему углу при каждой вершине многоугольника \(A_1A_2A_3. A_n\) . Тогда их сумма будет равна:

\(180^\circ-A_1+180^\circ-A_2+. +180^\circ-A_n=n\cdot180^\circ-(A_1+A_2+. +A_n)=n\cdot180^\circ-(n-2)\cdot180^\circ=n\cdot180^\circ-n\cdot180^\circ+2\cdot180^\circ=360^\circ\)

Определение 1.1.1. Плоская фигура называется выпуклой, если она целиком содержит прямолинейный отрезок, соединяющий любые две принадлежащие фигуре точки.

Так, на рис. 1.1.1 фигуры а), б), в) выпуклые фигуры, а фигура на рисунке 1.1.1 г) не выпукла. Круг и треугольник являются выпуклыми фигурами, четырехугольник же может быть как выпуклым, так и невыпуклым в зависимости от того, пересекаются ли его диагонали внутри или вне четырехугольника (рис. 1.1.2 а, б). [1, 38]

Определение 1.1.2. Пересечением двух (или нескольких) фигур называется фигура, состоящая из всех точек, принадлежащих обеим (или всем, если их несколько) фигурам.

Определение 1.1.3. Фигура называется ограниченной, если она целиком помещается внутри некоторой окружности. [8, 13]

Например, всякий параллелограмм, треугольник, круг, а также все фигуры, изображенные на рис. 1.1.1, являются ограниченными фигурами.

На рис. 1.1.3 изображено несколько неограниченных фигур; из них выпуклыми являются фигуры а) (полуплоскость), б) (полоса), в) (угол) и г).

По отношению ко всякой плоской фигуре все точки плоскости делятся на три категории: внутренние, внешние и граничные. [8, 14]

Определение 1.1.4. Точка фигуры называется внутренней, если существует круг (хотя бы очень малого радиуса) с центром в этой точке, целиком принадлежащий фигуре.

Внутренними точками фигуры будут, например, точки А и А' на рис. 1.1.4.

Определение 1.1.5. Точка называется внешней по отношению к фигуре, если существует круг с центром в этой точке, не содержащий точек фигуры.

Примером внешней точки по отношению к фигуре является точка В на рис. 1.1.4.

Определение 1.1.6. Точка фигуры называется граничной, если любой круг с центром в данной точке, всегда будет содержать как точки, принадлежащие фигуре, так и точки, не принадлежащие ей.

Например, точка С на рис. 1.1.4 является примером граничной точки фигуры. [7, 185]

Граничные точки фигуры образуют некоторую линию — кривую или ломаную. Эта линия называется границей фигуры. Если плоская линия является границей некоторой выпуклой фигуры, то она называется выпуклой кривой, или — в том случае, когда эта линия ломаная,— выпуклым многоугольником. [7, 186]

Определение 1.1.7. Выпуклым многоугольником называют и плоскую фигуру, и линию — границу этой фигуры.

Определение 1.1.8. Точками, принадлежащими фигуре, или, точками фигуры, называют все ее внутренние или граничные точки.

Определение 1.1.9. Если множество содержит все свои граничные точки, то оно называется замкнутым. Если же множество не содержит ни одной своей граничной точки, т.е. состоит из одних внутренних точек, то оно называется открытым. [7, 15]

Определение 1.1.10. Одномерные выпуклые фигуры это линии, обладающие тем свойством, что отрезок АВ, соединяющий любые две точки А и В такой линии, целиком принадлежит ей. [8, 16]

Одномерные выпуклые фигуры можно охарактеризовать как выпуклые фигуры, все точки которых являются граничными.

Двумерные (плоские) выпуклые фигуры могут быть весьма разнообразны (см., например, фигуры а), б), в) на рис. 1.1.1 и а), б), в), г) на рис. 1.1.3).

Определение 1.1.11. Отрезок это ограниченная одномерная выпуклая фигура.

Пусть Ф — произвольная плоская фигура.

Определение 1.1.12. Прямая l называется опорной прямой фигуры Ф, если она проходит хотя бы через одну граничную точку фигуры Ф и вся фигура Ф расположена по одну сторону от прямой l (рис. 1.1.5).

Например, прямая, проведенная через вершину треугольника параллельно противолежащей стороне (рис. 1.1.6, а), или сторона треугольника (рис. 1.1.6, 6) являются опорными прямыми треугольника; каждая сторона выпуклого многоугольника является его опорной прямой. Касательная к окружности является опорной прямой для круга, ограниченного этой окружностью (рис. 1.1.6, в). Опорная прямая может иметь с выпуклой ограниченной фигурой или единственную общую точку (см., например, рис. 1.1.6, а, в), или целый общий отрезок (рис. 1.1.6, б); если выпуклая фигура не ограничена, то опорная прямая может даже целиком принадлежать фигуре (рис. 1.1.6, г). [8, 18]

Опорную прямую выпуклой фигуры Ф можно также определить следующим образом:

Определение 1.1.13. Опорная прямая выпуклой фигуры Ф - это такая прямая, которая содержит граничные точки фигуры, но не содержит ни одной ее внутренней точки.

Действительно, прежде всего ясно, что опорная прямая не может содержать внутренней точки А фигуры: в противном случае точки фигуры Ф, расположенные внутри некоторой окружности с центром в точке А, находились бы по обе стороны от опорной прямой (рис. 1.1.7). С другой стороны, если прямая l не содержит внутренних точек выпуклой фигуры Ф, то вся фигура должна быть расположена по одну сторону от l. Действительно, пусть А — какая-нибудь внутренняя точка Ф. Если бы какая-либо (внутренняя или граничная) точка В фигуры находилась по другую сторону от прямой l, чем точка А (рис. 1.1.8), то точка пересечения прямой l с отрезком АВ была бы внутренней точкой Ф (см. задачу 1.1.3 а, б). [8, 19]

Теорема 1.1.1. К каждой ограниченной выпуклой фигуре можно провести в точности две опорные прямые, параллельные данному направлению.

Для того чтобы это доказать, проведем через каждую точку ограниченной выпуклой фигуры Ф прямую, параллельную данному направлению (рис. 1.1.9). Все эти прямые пересекают произвольную прямую, перпендикулярную к выбранному направлению, по одномерной выпуклой фигуре (если А и В — две произвольные точки пересечения нашей совокупности прямых с перпендикулярной к ним прямой, а С—произвольная точка отрезка АВ, то С тоже должна принадлежать этому пересечению; это нетрудно видеть из рис. 1.1.9, если воспользоваться выпуклостью фигуры Ф). Следовательно, это пересечение должно быть отрезком прямой линии (ограниченность пересечения вытекает из ограниченности фигуры Ф), а совокупность прямых, параллельных заданному направлению, проведенных через все точки Ф, должна представлять собой полосу. Крайние (граничные) прямые l₁ и l₂ этой полосы и являются двумя опорными прямыми, параллельными заданному направлению.

Теорема доказана. [8, 20]

Определение 1.1.14. Наибольшее расстояние между двумя точками плоской фигуры Ф называется диаметром фигуры.

Иначе говоря, диаметром фигуры Ф называется такое расстояние d, что, во-первых, расстояние между любыми двумя точками М и N фигуры Ф не превосходит d и, во-вторых, можно отыскать в фигуре Ф хотя бы одну пару точек А и В, расстояние между которыми в точности равно d. [1, 6]

Например, для круга диаметр, в указанном смысле, совпадает с обычным его диаметром (наибольшая из хорд).

Определение 1.1.15. Пусть К выпуклая кривая l’ и l’’ две ее параллельные опорные прямые. Расстояние h между этими опорными прямыми называется шириной кривой К в направлении перпендикулярном к прямым l’ и l’’ (рис. 1.1.10). [7, 198]

Определение 1.1.16. Наименьшую ширину выпуклой кривой К называют шириной К.

Определение 1.1.17. Совокупность лучей, исходящих из одной точки О, называется выпуклой, если она содержит все лучи, проходящие внутри угла, меньшего 180°, образованного любыми двумя лучами совокупности, не составляющими продолжение один другого.

Теорема 1.1.2. Выпуклая совокупность лучей может быть одним лучом, парой лучей, являющихся продолжением один другого, углом, меньшим 180°, полуплоскостью либо целой плоскостью (рис. 1.1.11).

В самом деле, из определения выпуклой совокупности лучей непосредственно следует, что пересечение такой совокупности с любой прямой, не проходящей через точку О, выпукло. Рассматривая пересечения выпуклой совокупности лучей, с двумя параллельными прямыми, расположенными по разные стороны от точки О, и учитывая, что каждое из этих пересечений может совсем не содержать точек, быть единственной точкой, отрезком, лучом или всей прямой, нетрудно выяснить, что выпуклая совокупность лучей может быть только одного из перечисленных выше видов; все возможные здесь случаи приведены на рис. 1.1.12. [8, 21]

Теорема доказана. [8, 22]

Пусть Ф — некоторая выпуклая фигура и О — ее граничная точка. Проведем из точки О лучи, соединяющие ее с каждой точкой (внутренней или граничной) фигуры Ф (рис. 1.1.13).

Мы получим выпуклую совокупность лучей. В самом деле, если ОА и ОВ — два луча данной совокупности (А и В — точки фигуры Ф), то все лучи, расположенные внутри острого угла АОВ, пересекают отрезок АВ, целиком состоящий из точек фигуры Ф, и, следовательно, принадлежат данной совокупности. [8, 22]

Получившаяся совокупность лучей не может быть единственным лучом или парой лучей, составляющих продолжение один другого, так как считается, что фигура не одномерна.

Нетрудно так же показать, что эта совокупность лучей не может заполнить всю плоскость. Действительно, если лучи заполняют плоскость, то среди них можно выбрать две такие пары лучей ОА и ОВ, ОС и ОD, что лучи каждой пары, составляют продолжение один другого. Пусть А, В, С, D—точки выпуклой фигуры, лежащие на этих лучах (рис. 1.1.14). Фигура Ф вместе с точками А, В, С должна содержать весь треугольник АВС (см. рис. 1.1.14) и вместе с точками А, В, D—весь треугольник АВD, т. е. она должна содержать весь выпуклый четырехугольник АСВD, для которого точка О является внутренней. Таким образом, в этом случае точка О не может быть граничной точкой фигуры Ф. [8, 23]

Следовательно, рассматриваемая совокупность лучей будет либо полуплоскостью, либо углом, меньшим 180°. В первом случае (рис. 1.1.15) точка О называется обыкновенной точкой выпуклой кривой К, ограничивающей фигуру Ф.

Прямая Г, ограничивающая полуплоскость, является опорной прямой фигуры Ф (все точки Ф лежат на лучах нашей совокупности, а следовательно, с одной стороны от прямой Г).

Рис. 1.1.15 Рис. 1.1.16

При этом прямая Г является единственной опорной прямой фигуры Ф в точке О, так как по обе стороны от каждой другой прямой l, проходящей через О, есть лучи нашей совокупности, а следовательно, и точки фигуры Ф (рис. 1.1.15). Такая опорная прямая Г фигуры Ф, ограничивающая полуплоскость, называется касательной в точке О к выпуклой кривой К. [7, 188]

Во втором случае, когда выпуклая совокупность лучей является углом, меньшим 180°, точка О называется угловой точкой выпуклой кривой К, ограничивающей фигуру Ф (рис. 1.1.16).

Все точки фигуры Ф заключены в этом случае внутри угла МОN; поэтому всякая прямая l, проходящая внутри угла МОN’, смежного с углом МОN, будет опорной прямой фигуры Ф. В частности, опорными будут и лучи ОМ, ОN, которые называются полукасательным в точке О к выпуклой кривой К, ограничивающей фигуру Ф. [1, 40]

Определение 1.1.18. Угол MON = называется внутренним углом (или просто углом) выпуклой кривой К или выпуклой фигуры Ф в точке О, а угол МОN’ =180° - называется внешним углом кривой К или выпуклой фигуры Ф. [7, 189]

Согласно этому определению все точки выпуклого многоугольника, кроме вершин, являются обыкновенными, причем касательными в этих точках являются стороны многоугольника. Вершины выпуклого многоугольника являются его угловыми точками, а определенные выше углы совпадают с углами многоугольника в обычном смысле (рис. 1.1.17).

Сопоставляя оба случая — случай обыкновенной точки выпуклой кривой и случай угловой точки, приходим к заключению, что через каждую точку выпуклой кривой проходит, по крайней мере, одна опорная прямая. [1, 41]

Определение 1.1.19. Ограниченная фигура называется выпуклой, если через каждую ее граничную точку проходит, по крайней мере, одна опорная прямая. [8, 26]

Пусть Ф — произвольная ограниченная выпуклая фигура, К— ее граница. Установим на кривой К определенное направление обхода, например, против часовой стрелки. При движении по кривой К в этом направлении фигура Ф все время остается слева (рис. 1.1.18). В соответствии с этим установим направления и на опорных прямых фигуры Ф.

Будем выбирать направление опорной прямой l фигуры Ф таким образом, чтобы фигура Ф лежала слева от прямой l (рис. 1.1.19).

Рис. 1.1.18 Рис. 1.1.19

В таком случае две параллельные между собой опорные прямые l₁ и l₂ фигуры Ф получат противоположные направления. Таким образом, каждому направлению в плоскости (которое можно задавать при помощи прямой со стрелкой) будет соответствовать единственная опорная прямая, имеющая это направление (рис. 1.1.19).

Если К это многоугольник, то задание направления обхода позволяет говорить о направлениях сторон многоугольника.

Определение 1.1.20. п граничных точек А, В, С, . , Р фигуры Ф расположены в циклическом порядке, если при обходе кривой К, ограничивающей фигуру Ф, против часовой стрелки эти точки встречаются в указанном порядке

Определение 1.1.21. Если точки А, В, С, . Р кривой К расположены в циклическом порядке, то многоугольник АВС. Р называется вписанным в кривую К.

Определение 1.1.22. Если l₁, l₂, . , l_п это п опорных прямых выпуклой фигуры Ф, на каждой из которых установлено направление, а П₁, П₂, . , П_n - соответствующие им левые полуплоскости (рис.1.1.21), то Ф расположена в каждой из этих левых полуплоскостей, а значит, и в их пересечении. Если это пересечение ограничено, т. е. является многоугольником, то этот многоугольник называется описанным вокруг фигуры Ф или вокруг ограничивающей ее кривой К. [8, 27]

Из этого определения следует, что многоугольник, описанный вокруг выпуклой фигуры, всегда является выпуклым. Сторонами описанного многоугольника являются отрезки прямых l₁, l₂, . , l_п.

Может, однако, оказаться, что три (или больше) из взятых п опорных прямых будут проходить через одну и ту же граничную точку фигуры Ф (которая в этом случае обязательно является угловой; рис. 1.1.22). В таком случае описанный многоугольник будет иметь меньше чем п сторон. Такой многоугольник называют n-угольником, имеющим одну или несколько сторон нулевой длины, т. е сторон, превратившихся в точки. Эти стороны нулевой длины имеют определенные направления, а именно направления соответствующих опорных прямых

Это позволяет говорить об п внутренних и внешних углах описанного n-угольника независимо от того, имеет ли он стороны нулевой длины или нет.

Определение 1.1.23. Длиной ограниченной выпуклой кривой К и площадью фигуры Ф, которую эта кривая ограничивает, называются пределы периметров, соответственно площадей, вписанных в Ф многоугольников, все стороны которых безгранично уменьшаются, или описанных вокруг Ф многоугольников, все внешние углы которых безгранично уменьшаются.

Из этого определения следует, что если выпуклая кривая К целиком заключена внутри выпуклой кривой К’, то длина К не может быть больше длины К’.

Теорема 1.1.3. Если выпуклая кривая К целиком заключена внутри выпуклой кривой К’, то длина К не может быть больше длины К’.

Действительно, рассмотрим последовательность многоугольников, вписанных в кривую К, стороны которых безгранично уменьшаются, и последовательность многоугольников, описанных вокруг К’, внешние углы которых безгранично уменьшаются (рис. 1.1.23).

Каждый из многоугольников второй последовательности заключает в себе каждый из выпуклых многоугольников первой последовательности и, следовательно, имеет больший периметр; отсюда следует, что предел периметров многоугольников второй последовательности — длина К’ не меньше предела периметров многоугольников первой последовательности — длины К.

Определение 1.1.24. Периметром плоской фигуры называется длина кривой, ограничивающей эту фигуру. [8, 28]

Раздел: Математика
Количество знаков с пробелами: 92071
Количество таблиц: 0
Количество изображений: 61

Читайте также: