Как решать интегралы кратко и понятно

Обновлено: 28.06.2024

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Интегрирование было популярно ещё в давние времена. Хотя это не использовалась в текущем варианте, но всё же. В ту эпоху математики написали книги на эту тему. Ньютон и Лейбниц отличались своими особенностями, но смысл вообще не поменялся.

Прежде чем выяснить такое определение, вам всё еще необходимо базовое понимание принципов математического изучения.

Неопределённый интеграл

Предположим, мы используем данную функцию наподобие символов f (x).

Непонятный интеграл f (x) – это формула с двумя буквами F (x), производная которой равна формула с двумя буквами f (x).

Так или иначе, называется обратной производной или обратным интегралом. Кстати, рекомендуем прочесть статью про то, как их рассчитать.

Он имеется для всех постоянных функций. Кроме того, нередко добавляется символ константы, поскольку производные различных функций константы подобны. Действие интегрального поиска – вот потому и является интеграцией.

Чтобы регулярно не пересчитывать примитивные простых функций, их пригодно объединить в таблицу и использовать готовую значительность.

Определенный интеграл

Это определение называется постоянной малой степенью, способная определить площадь фигуры, массу неоднородного тела, путь, по которому находится переменное движение и прочее. Стоит знать, что это сумма постоянно множества безмерно небольших слагаемых.

Для поиска площади фигуры по узкому графику функции необходимо использовать интеграл! Неровную трапецию, узкую по координатным осям и графику функции разделим на безмерно небольшие части. Это разделит фигуру на тонкие столбцы. Сумма величины столбцов является величиной трапеции. Однако не стоит забывать, что подобный расчёт придаст приблизительный итог. Но чем менее и уже сегменты, тем вернее станет расчётом. При их сокращении величина приблизится к нулевой отметки. Тогда сумма площадей сегментов устремится к площади фигуры.

Расстояние a и b являются пределами интегрирования. Для примера можно составить подобный график.

Правила вычисления для чайников

Свойства неопределенного интеграла

Перед тем как решать, проанализируем самые подходящие особенности, пригодные для решения элементарных примеров.

Прежде всего, мы подчеркнём, что данное равенство относительное. Его следует понимать как равенство правой и левой частей с определённостью до любого постоянного слагаемого, поскольку каждый из них вычислен с определённостью до любого постоянного слагаемого.

Собственно, пусть F (x) – это будет интеграл для функции f (x), то бишь F’ (x) = f (x) Значит AF (x) – это для функции, Af (x), поскольку [AF (x)]’ = AF’ (x) = Af (x).

Данное равенство (также и в предыдущем свойстве) следует понимать как равенство правого и левого элементов с определённостью до свободного одинакового слагаемого, поскольку каждый из них вычислен с определённостью до свободного одинакового слагаемого.

Собственно, пусть F(x) и G(x) – используются для таких математических символов: f (x) и g (x), то бишь F’(x) = f(x), G’(x) = g(x). Значит F(x) + G(x) – это интеграл для математических символов, f (x) = g (x), поскольку [F(x) = G(x)’] = F’(x) + G’(x) = f(x) = g(x).

Подчеркнём, что это свойство объективно для любого конечного числа слагаемых функции.

Свойства определенного интеграла

Как его рассчитать? Для этого нужна формула Ньютона-Лейбница.

Мы уже узнали, что предельная сумма – это конкретный интеграл.

Допустим, формула y = f(x) обусловлена в интервале [a, b], a

1) сперва мы разделим [a, b] точками a = x0

2) в каждом из фрагментарных отрезков [xi-1, xi], i = 1, 2, . n, мы выбираем случайную точку и вычисляем в ней значимость функции: f (zi);

3) находим действия f (zi) · Δxi, где – длина неполного разреза [xi-1, xi], i = 1, 2, . n;

4) создадим совокупную сумму y = f(x) на отрезке [a, b]

С учётом геометрии такая совокупность составляет необходимую сумму площадей прямоугольников, подтверждениями которых являются выборочные отрезки [x0, x1], [x1, x2], …, [xi-1, x1], …, [xn-1, xn], но высоты одинаковы f (z1), f (z2), . f (zn) сообразно.

Когда имеется последний предел объединенной суммы, и он не связан с особенностью деления на выборочные отрезки или выбора точек zi внутри них, то – это конкретный интеграл функции y = f (x) на отрезке [a, b].

Примеры решения интегралов

Интеграл является одним из наиболее важных понятий в математическом анализе. Его применяют в алгебре для расчета площади под кривой, преодоленного пути в процессе неравномерного движения, массы, которой обладает неоднородное тело и решения других подобных задач. С помощью интеграла вычисляют функцию по известной производной.

Интегралы для чайников — базовые понятия

Понятие интеграла в теории основано на нахождении непрерывной функции. Для начала следует ознакомиться с этим термином.

Непрерывная функция F(х) представляет собой первообразную функции f(х) на понятном промежутке х при условии, что F(х)=f(х).

Процедура поиска первообразной функции f(х) представляет собой операцию интегрирования в определенном порядке.

Интеграл в кратком смысле является аналогом суммы для бесконечного числа бесконечно малых слагаемых.

Неопределенный интеграл

Неопределенным интегралом называют комплекс всех первообразных функции f(х).

В легком виде формулу для расчета неопределенного интеграла можно записать в такой форме:

\(\int f(x)dx=F(x)+C\) , где

f(x) является подынтегральной функцией;
F(x) представляет собой первообразную функцию функции f(x);
dx определяется дифференциалом;
C является численной константой интегрирования.

В неопределенный интеграл включен спектр первообразных, так как имеется постоянная интегрирования. Дифференциалом называют произвольное, бесконечно малое приращение переменной величины. Среди основных свойств неопределенного интеграла можно отметить такие пояснения:

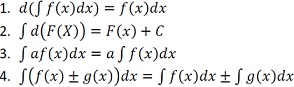
Табличная форма неопределенных интегралов в виде \(\int f(x)dx=F(x)+C\) имеет вид:

Определенный интеграл

Определенным интегралом называют приращение одной из первообразных функции f(х), соответствующих отрезку [a;b].

В общем виде определенный интеграл можно записать таким образом:

f(x) представляет собой подынтегральную функцию;
a и b являются пределами интегрирования;
dx соответствует дифференциалу.

Вычислить определенный интеграл можно с помощью уравнения Ньютона-Лейбница:

Свойства определенных интегралов:

если определенный интеграл обладает одинаковыми пределами интегрирования, то его значение соответствует нулю;
значение определенного интеграла является независимой от обозначения переменной интегрирования величиной;
постоянный множитель допустимо выносить за знак определенного интеграла;
определенный интеграл в случае алгебраической суммы конечного числа функций рассчитывается как алгебраическая сумма определенных интегралов;
при разбивке отрезка интегрирования на части определенный интеграл в отношении всего отрезка соответствует сумме определенных интегралов его частей;
перестановка пределов интегрирования не меняет абсолютную величину определенного интеграла, а изменяет его знак;
определенный интеграл рассчитывается как произведение длины отрезка интегрирования и значения подынтегральной функции в какой-то точке х0 внутри него;
в том случае, если верхний предел интегрирования больше, чем нижний, и подынтегральная функция соответствует неотрицательному или положительному значению, определенному интегралу будет соответствовать неотрицательная или положительная величина;
когда верхний предел интегрирования больше, чем нижний, и функции f(х) и g(х) не прерываются, то допустимо почленно интегрировать неравенство f(x) >=g(x).

Таблица интегралов для студентов (основные формулы)

Существует несколько основных приемов решения задач с интегралами. Процесс заключается в интегрировании функции по переменной. В том случае, если интеграл обладает табличным видом, то проблем с поиском его значения не возникнет. Когда форма записи интеграла отлична от табличной, решение сводится к приведению интеграла к табличному виду.

Таблица первообразных для решения интегралов имеет следующий вид:

В первую очередь необходимо ознакомиться с основными свойствами интегралов:

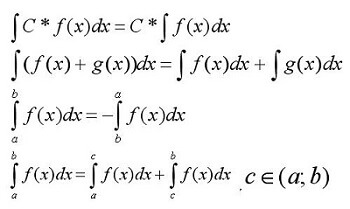
С помощью данных понятий можно решать несложные интегралы. Но в большинстве случаев встречаются задачи с непростыми интегралами, для работы с которыми требуется прибегнуть к дополнительным приемам.

Правила вычисления интегралов, примеры решения

Специальные методики позволяют рассчитывать большую часть интегралов. Основными приемами для поиска решений являются:

Замена переменной с применением навыков нахождения производных.

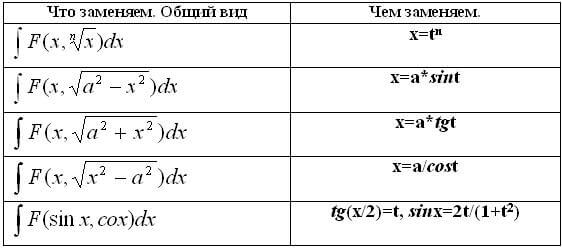
Решать интегралы целесообразно с помощью данного алгоритма:

Вникнуть в суть интегралов, включая базовые понятия и методы решения. Интеграл представляет собой сумму элементарных частей объекта интегрирования. В том случае, когда рассматривается интегрирование функции, следует идентифицировать интеграл как площадь фигуры между графиком функции, осью х и границами интегрирования. При неопределенном интеграле, то есть неизвестных границах интегрирования, решать задачу необходимо с помощью нахождения первообразной. В случае определенного интеграла в найденную функцию подставляют значения границ.
Научиться пользоваться таблицей первообразных и основными свойствами интегралов. Множество функций уже определены первообразными, которые отмечены в таблице. Для интегралов, которые занесены в табличную форму, уже имеется готовое решение.
Освоение способов и приобретение навыков решения интегралов. В том случае, когда в задаче имеется интеграл, не соответствующий табличной форме, его необходимо привести к этому виду. Данная операция выполняется с помощью применения основных свойств интегралов и приемов по их решению.

На первых этапах обучения следует проверять собственные решения задач на интегралы. Для этого можно дифференцировать полученное выражение и сравнить его с исходным интегралом.

Примеры решения интегралов:

Задача 1

Требуется решить интеграл:

Решение

Заметим, что по условию интеграл — неопределенный. Сначала необходимо найти первообразную. Для этого интеграл суммы можно разложить на сумму интегралов:

Таким образом, каждый из интегралов преобразован в табличный вид. Решение можно найти с помощью таблицы:

Выполним проверку решения с помощью поиска производной:

Задача 2

Требуется решить интеграл:

Решение

Имеется неопределенный интеграл. Для начала необходимо найти первообразную. При сравнении с таблицей выяснилось, что подобное решение отсутствует. Способ разложения, исходя из свойств интеграла, не применим в данном случае. Следует обратиться к приемам. В этом случае целесообразно воспользоваться заменой переменной. Таким образом, выполним замену выражения \(х+5\) на \(t^\) .

После преобразований получим \(\int tdx.\)

Выражение dx также требуется заменить на t. В таком случае:

Выполним подстановку значений:

Интеграл соответствует табличной форме. Его можно посчитать \(\frac>\) .

Далее необходимо заменить t на выражение \(\sqrt[5]\) .

Задача 3

Необходимо найти решение интеграла:

Решение

В рамках данной задачи целесообразно выделить полный квадрат:

Результат преобразований соответствует табличному виду. Можно найти первообразную:

В результате получим:

Математический анализ — достаточно сложная дисциплина. Одной из главных тем является решение интегралов. С подобными задачами часто сталкиваются учащиеся профильных вузов. Если в процессе обучения студент испытывает какие-либо трудности, правильное решение — обратиться к сервису Феникс.Хелп.

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Производная от интеграла равна подынтегральной функции:

Константу можно выносить из-под знака интеграла:

Интеграл от суммы равен сумме интегралов. Верно также для разности:

Свойства определенного интеграла

Знак интеграла изменяется, если поменять местами пределы интегрирования:

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.

Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:

вычисление площади фигуры.
вычисление массы тела с неравномерной плотностью.
определение пройденного пути при движении с непостоянной скоростью.
и др.

Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.

Главная причина незнания – отсутствие понимания практической значимости интегралов.

Нужна помощь в написании работы?

Мы - биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Интеграл – что это?

Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.

Метод исчерпывания для определения площади круга

В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.

Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.

Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.

Интеграл записывается так:

Неопределённый интеграл

Неопределенный интеграл не имеет границ интегрирования.

Определённый интеграл

Точки A и B на оси X – есть ограничение зоны определения интеграла

Таблица интегралов для студентов (основные формулы)

Скачайте формулы интегралов, они вам еще пригодятся

Как вычислять интеграл правильно

Существует несколько простейших операций для преобразования интегралов. Вот основные из них:

Вынесение константы из-под знака интеграла

Разложение интеграла суммы на сумму интегралов

Если поменять местами a и b, знак изменится

Можно разбить интеграл на промежутки следующим образом

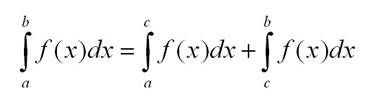
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.

Примеры вычисления интегралов

Решение неопределенного интеграла

Решение определенного интеграла

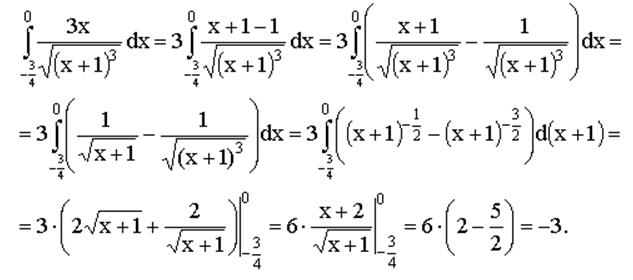
Базовые понятия для понимания темы

Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.

Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.

Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.

Приращение – количественное изменение функции при некотором изменении аргумента.

Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.

Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.

Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.

Заключение

Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.

Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:

Интегралы – что это, как решать, примеры решений и объяснение для чайников обновлено: 16 апреля, 2020 автором: Научные Статьи.Ру

Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная дифференцированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .

Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:

Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:

Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.

F(x) – первообразная. Дифференцируя первообразную, мы получим исходное подынтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференцируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:

Таблица первообразных для решения интегралов

Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:

Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.

Основные приемы решения интегралов

1. Замена переменной.

Для выполнения данного приема потребуется хороший навык нахождения производных.

2. Интегрирование по частям. Пользуются следующей формулой.

Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.

3. Интегрирование дробно-рациональных функций.
- разложить дробь на простейшие
- выделить полный квадрат.
- создать в числителе дифференциал знаменателя.

4. Интегрирование дробно-иррациональных функций.
- выделить под корнем полный квадрат
- создать в числителе дифференциал подкоренного выражения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin 2 +cos 2 =1
m,n – четные, sin 2 x=(1-cos2x)/2 и cos 2 x=(1+cos2x)/2
Для выражений вида:
- Применяем свойство tg 2 x=1/cos 2 x - 1

С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:

1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференцируем полученное выражение и сравниваем с исходным интегралом.
Отработаем основные моменты на нескольких примерах:

Примеры решения интегралов

Пример 1:
Решить интеграл:

Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.

Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла:

Проверим решение(найдем производную):

Пример 2. Решаем интеграл

Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t 5 . t 5 = x+5 . Получаем.

Но dx нужно тоже заменить на t. x= t 5 - 5, dx = (t 5 - 5)’ = 5t 4 . Подставляем:

Интеграл из таблицы. Считаем:

Подставляем в ответ вместо t ,

Пример 3. Решение интеграла:

Для решения в этом случае необходимо выделить полный квадрат. Выделяем:

В данном случае коэффициент 1/2 перед интегралом получился в результате замены dx на 1/2*d(2x+1). Если вы найдете производные x’ = 1 и 1/2*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную.

В итоге получаем:

Для закрепления темы интегралов рекомендуем также посмотреть видео.

В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.

Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.

Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию . Программирование одна из дочек математики!

Читайте также: