Как распределена энергия магнитного поля соленоида в пространстве кратко

Обновлено: 05.07.2024

Магнитное поле, создаваемое токами, распределено в пространстве. Рассмотрим, какова плотность энергии поля изолированного контура с током. Используем выражение для энергии магнитного поля, которое создано контуром с током:

где $I$ - сила тока в контуре; L – индуктивность контура.

Примем во внимание, что магнитный поток индукции через фиксированную неподвижную площадку пропорционален силе тока, а именно:

$Ф=LI\left( 2 \right)$.

Из формулы (2) получим, что индуктивность контура равна:

тогда энергия магнитного поля может быть представлена как:

Магнитный поток из своего определения равен:

$Ф=\int\limits_S \bullet d\vec\left( 5 \right),>$

где $S$ – площадь поверхности контура с током. Вектор индукции магнитного поля запишем через векторный потенциал магнитного поля ($\vec A$), который создается током $I$:

Тогда выражение (5) приведем к виду:

где $L$ - контур тока.

Физическая сущность данного взаимодействия заключается в том, что всякий элемент тока $I\vec dl$ порождает в пространстве магнитное поле. С этим полем входят во взаимодействие все остальные элементы контура.

Подставим выражение для магнитного потока (7) в формулу для энергии (2), найдем:

где сделан переход к объемным токам при помощи соотношения:

Готовые работы на аналогичную тему

$\vecdV\leftrightarrow Id\vec\left( 9 \right)$,

$\vec j$ – вектор плотности тока.

Стрелка в выражении (9) показывает, что данная замена дает возможность перейти от формул для объемных токов к формулам линейных токов и в обратную сторону.

Преобразуем выражение под интегралом так, чтобы в него входили только векторы поля и векторный потенциал. Используем формулы (6) и

Вспомним известное соотношение для дивергенции векторного произведения:

Получим в результате:

тогда выражение для энергии примет вид:

Будем считать, что все токи находятся в конечной области пространства. Тогда на больших расстояниях ($r$) от области локализации токов мы будем иметь:

В результате мы получаем, что подынтегральное выражение убывает пропорционально $\sim \frac>$ . При этом поверхность интегрирования увеличивается пропорционально квадрату расстояния ($\sim \frac>$). Вывод: с ростом расстояния от места расположения токов интеграл (14) убывает пропорционально расстоянию ($\sim \frac$). Следовательно, для всего пространства, когда $r\to \infty$ интеграл (4) стремится к нулю. Полную энергию магнитного поля представим в виде:

Из выражения (15) следует, что объемная плотность распределения энергии магнитного поля равна:

Плотностью энергии магнитного поля называют его энергию, сосредоточенную в единице объема этого поля.

Представленное выражение справедливо для равномерного распределения энергии поля по объему.

Формула (16) говорит нам о том, что объемная плотность энергии магнитного поля в каждой его точке определяют значения векторов поля в этой точке, и не имеет значение каковы источники поля.

Для однородного изотропного магнетика мы имеем следующую связь между векторами поля:

$\vec=\mu \mu_\vec\left( 17 \right)$.

Используя формулу (17) выражения для нахождения плотности магнитного поля представим как:

В Международной системе единиц (СИ) плотность энергии магнитного поля измеряется в джоулях, деленных на кубометр ($Дж/м^3$ ).

Энергия магнитного поля при наличии магнетиков

Допустим, что все пространство заполняет однородный магнетик. В этом случае создаваемая токами индукция будет изменяться в $\frac<\mu ><\mu_>$ раз в сравнении с индукцией в вакууме. ($\mu$ – магнитная проницаемость вещества; $\mu_$ – магнитная постоянная). Это означает, что во столько же раз изменятся потоки $Ф$ и $dФ$. Из формулы (2) заключим, что индуктивность контура и взаимные индуктивности увеличатся в $\frac<\mu ><\mu_>$ раз. Формула (1) для энергии магнитного поля не изменится, но в ней индуктивность изменится в $\frac<\mu ><\mu_>$ раз.

Можно сделать вывод о том, что энергия магнитного поля токов, которые текут в неограниченном однородном магнетике, изменится в $\frac<\mu ><\mu_<0>>$ раз в сравнении с энергией поля этих же самых токов в вакууме. Аналогичный вывод можно сделать относительно плотности энергии.

Ограниченность формул для вычисления плотности энергии

Допущения, сделанные нами, которые заставляют говорить об ограничениях применения формул, полученных нами для плотности энергии магнитного поля:

Мы предполагали, что вещество, в котором токи создают магнитные поля, является магнитоизотропным. Магнитная проницаемость среды постоянная величина.
Мы не учитывали, что поле осуществляет намагничивание вещества.

Вопрос о локализации энергии магнитного поля

Для постоянных магнитных полей, которые создаются неподвижными постоянными токами, непонятно, где локализуется энергия. Возьмем выражение для магнитной энергии соленоида:

где $Ѱ=BSN$ – потокосцепление, то есть магнитный поток через витки соленоида. В этом энергия поля кажется энергией тока, так как он является носителем.

Однако энергию соленоида можно представить и так:

где присутствуют параметры самого соленоида и характеристика магнитного поля ($B$), что говорит о том, что энергия поля распределена по объему поля.

Для постоянных магнитных полей эта непонятность вызвана тем, что токи и поля существуют неразрывно, образуя систему.

При переходе к переменным магнитным полям приемлемой становится только полевая концепция магнитной энергии, так как переменные магнитные поля входят как компоненты электромагнитных полей и могут существовать самостоятельно от токов. Электромагнитные волны переносят энергию, значит, сделаем вывод о том, что энергия магнитного поля распределена в объеме поля.

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток Φ , который проходит через контур или катушку с током, является пропорциональным силе тока I : Φ = L I .

Коэффициент пропорциональности L в формуле Φ = L I есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в С И носит название генри ( Г н ) . Индуктивность контура или катушки равна 1 Г н , когда при силе постоянного тока 1 А собственный поток составляет 1 В б : 1 Г н = 1 В б 1 А .

Расчет индуктивности

Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l . Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:

где I является обозначением тока в соленоиде, n = N e указывает число витков на единицу длины соленоида.

Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:

Φ = B · S · N = μ 0 n 2 S l

Таким образом, индуктивность соленоида будет выражена формулой:

L = μ 0 n 2 S · l = μ 0 n 2 V ,

где V = S l – объем соленоида, содержащий магнитное поле.

Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ , при заданном токе I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:

L μ = μ · L = μ 0 · μ · n 2 · V .

ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:

δ и н д = δ L = - ∆ Φ ∆ t = - L ∆ I ∆ t .

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1 . 21 . 1 ). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Рисунок 1 . 21 . 1 . Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как R полное сопротивление цепи, тогда за время Δ t будет выделено количество теплоты Δ Q = I 2 · R · Δ t .

Ток в цепи составляет:

I = δ L R = - L R ∆ I ∆ t

Выражение для Δ Q можем записать так:

∆ Q = - L · I · ∆ I = - Φ ( I ) ∆ I

В данной записи Δ I 0 ; значение тока в цепи постепенно снижается от изначального I 0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I 0 до 0 . Тогда получим:

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ ( I ) от тока I (рис. 1 . 21 . 2 ). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1 . 21 . 2 треугольника:

Рисунок 1 . 21 . 2 . Вычисление энергии магнитного поля.

В итоге формула энергии W м магнитного поля катушки с индуктивностью L , создаваемого током I , будет записана в виде формулы:

W м = Φ I 2 = L I 2 2 = Φ 2 2 L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции L μ соленоида и для магнитного поля B, создаваемого током I , получим запись:

W м = μ 0 · μ · n 2 · I 2 2 V = B 2 2 μ 0 · μ V

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: W м = B 2 2 μ · μ .

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

36) Энергия магнитного поля.

Рассмотрим цепь, изображенную на рис. 115. Сначала замкнем соленоид L на батарею ε в нем установится ток i; который обусловит магнитное поле, сцепленное с витками соленоида.

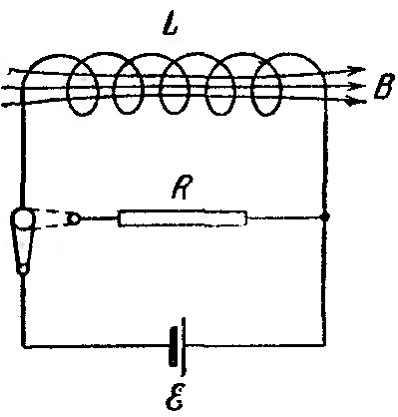
Если, отключив соленоид от батареи, замкнуть его через сопротивление R, то в образовавшейся цепи будет некоторое время течь постепенно убывающий ток. Работа, совершаемая этим током за время dt, равна

dA = ε S i dt = – (d ψ /dt)idt = – id ψ . (61.1)

Если индуктивность соленоида не зависит от t (L = const), то d ψ = Ldi и выражение (61.1) принимает следующий вид:

Проинтегрировав это выражение по i в пределах от первоначального значения i до нуля, получим работу, совершаемую в цепи за все время, в течение которого происходит исчезновение магнитного поля:

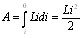
(61.3)

Работа (61.3) идет на приращение внутренней энергии проводников, т. е. на их нагревание. Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем соленоид пространстве.1 Поскольку никаких других изменений в окружающих электрическую цепь телах не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается работа (61.3). Таким образом, мы приходим к выводу, что проводник с индуктивностью L, по которому течет ток i, обладает энергией

которая локализована в возбуждаемом током магнитном поле [ср. эту формулу с выражением для энергии заряженного конденсатора].

Заметим, что выражение (61.3) можно трактовать как ту работу, которую необходимо совершить против э. д. с. самоиндукции в процессе нарастания тока от 0 до i, и которая идет на создание магнитного поля, обладающего энергией (61.4). В самом деле, работа, совершаемая против э. д. с. самоиндукции,

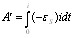
Произведя преобразования, подобные тем, которые привели нас к выражению (61.2), получим

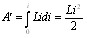
(61.6)

что совпадает с (61.3). Работа (61.6) совершается при установлении тока за счет источника э. д. с. и идет целиком на создание сцепленного с контуром магнитного поля. Выражение (61.6) не учитывает той работы, которую источник э. д. с. затрачивает в процессе установления тока на нагревание проводников. Она равна

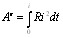
Выразим энергию магнитного поля (61.4) через величины, характеризующие само поле. В случае бесконечного (практически очень длинного) соленоида

L = μ 0 μ n 2 V, Н = ni,

Подставляя эти значения L и i в (61.4) и производя преобразования, получим

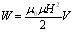
(61.7)

Было показано, что магнитное поле бесконечно длинного соленоида однородно и отлично от нуля только внутри соленоида. Следовательно, энергия (61.7) заключена в пределах соленоида и распределена по его объему с постоянной плотностью w, которую можно получить, разделив W на V. Произведя это деление, получим

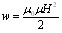
(61.8)

Воспользовавшись соотношением (44.15), формулу для плотности энергии магнитного поля можно записать следующим образом:

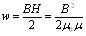
(61.9)

Полученное нами выражение для плотности энергии магнитного поля имеет вид, аналогичный выражению (30.2) для плотности энергии электрического поля, с тем лишь отличием, что электрические величины в нем заменены соответствующими магнитными.

Если магнитное поле неоднородно, плотность энергии больше там, где больше Н и μ . Чтобы найти энергию магнитного поля, заключенную в некотором объеме V, нужно вычислить интеграл

Энергия магнитного поля — величина, обозначающая работу, затраченную электрическим током в проводнике или катушке индуктивности на образование этого магнитного поля.

Описание явления, закон Фарадея

Магнитное поле обладает энергией. Данный факт можно доказать с помощью практического эксперимента. Опыт заключается в исследовании процесса убывания силы тока в катушке при отключении от нее источника тока. Предположим, что до того момента, когда был разомкнут ключ, в катушке имелся ток I, что способствовало образованию магнитного поля. После размыкания ключа катушка и сопротивление соединяются последовательно. В результате самоиндукции ток в катушке будет постепенно уменьшаться. Процесс сопровождается выделением теплоты на сопротивлении. Источник тока отключен, поэтому необходимо определить источник энергии, которая расходуется на тепло. Так как убывает ток и создаваемое им магнитное поле, допустимо говорить о понятии энергии тока или энергии магнитного поля, которое он создает.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В том случае, когда магнитное поле образовано постоянным током, определить место сосредоточения энергии не представляется возможным, так как ток по своему свойству образует магнитное поле, которое в любом случае сопровождается токами. Можно рассмотреть переменное магнитное поле в электромагнитной волне. Такая волна характеризуется наличием магнитных полей в условиях отсутствия токов. Известно, что электромагнитные волны являются переносчиками энергии, что позволяет сделать вывод о существовании энергии в магнитном поле. Таким образом, электрический ток обладает энергией, локализованной в магнитном поле, то есть в среде, окружающей этот ток. Согласно закона сохранения энергии, на примере эксперимента вся энергия магнитного поля выделяется в виде Джоулева тепла на сопротивлении R.

Электромагнитная индукция представляет собой явление возникновения электрического тока, поля или электрической поляризации при изменении с течением времени магнитного поля или в процессе движения материальной среды в нем.

С помощью опытов с катушками и магнитом Фарадею удалось обнаружить зависимость между величиной электродвижущей силы и скорости, с которой перемещаются катушки или магнит. Данное наблюдение послужило основанием для выявления закономерности и формулировки закона электромагнитной индукции.

Закон электромагнитной индукции: электродвижущая сила пропорциональна скорости изменения магнитного потока, проходящего через контур.

E — электродвижущая сила; $\Delta \Phi$ — изменение магнитного потока; $\Delta t$ — время, в течение которого происходило изменение магнитного потока.

Единицами измерения ЭДС являются вольты магнитного потока — веберы. $\Delta$ определяет разницу между конечным и начальным параметром.

Формула закона Фарадея содержит знак минуса. К данному выражению применено правило Ленца, как пояснение того, что ток, образовавшийся в результате индукции, в любом случае противоположно направлен образующему его магнитному потоку. Магнитное поле индукционного тока всегда препятствует магнитному потоку из внешнего источника. По смыслу правило схоже с законом сохранения энергии.

Связь энергии магнитного поля и его основных характеристик

На примере длинного соленоида можно рассмотреть проявление энергии магнитного поля. Предположим, что поля является однородным и сосредоточено внутри соленоида. В таком случае, для нахождения силы тока можно воспользоваться формулой:

Здесь H — напряженность магнитного поля соленоида; l — длина соленоида; N — число витков соленоида.

В случае эксперимента с соленоидом:

Здесь $\mu$ — магнитная проницаемость сердечника соленоида; S — площадь сечения соленоида; n=Nl.

Как правило, роль энергетической характеристики магнитного поля играет такой параметр, как плотность энергии магнитного поля:

Данное выражение справедливо в случае любого магнитного поля, несмотря на характер его происхождения. Формула определяет энергию магнитного поля в единице его объема. Если имеется магнитоизотропная среда, то уравнение можно преобразовать, таким образом:

В случае неоднородного магнитного поля целесообразно разбить его на элементарные объемы (dV), то есть малые объемы, в которых магнитное поле считается однородным. Энергия магнитного поля, заключенная в рассматриваемых объемах, составляет:

При этом суммарная энергия магнитного поля равна:

Интегрированию в данном случае подлежит весь объем, занимаемый магнитным полем.

От чего зависит величина

Существует ряд некоторых ограничений в применении формулы для расчета энергии магнитного поля. При записи выражения выполнялось несколько условий:

индуктивность контура, а также магнитная проницаемость вещества стабильны;
вся энергия источника тока трансформируется в энергию магнитного поля.

Перечисленные условия справедливы лишь в случае вакуума, то есть при $\mu$ =1. Если контур с током поместить в вещество, то необходимо принимать во внимание следующие параметры:

намагничивание вещества, что способствует его нагреву;
объем и плотность вещества в магнитном поле могут изменяться даже при стабильной температуре.

Таким образом, магнитная проницаемость вещества $\mu$ , изменяющаяся при перепадах температуры и плотности среды, не может оставаться постоянной в процессе намагничивания. Также работа источника ЭДС не полностью трансформируется в энергию магнитного поля. В том случае, когда объем вещества изменяется в малой степени, сохраняется стабильной температура среды, внешняя работа затрачивается на увеличение энергии магнитного поля $E_$ и на теплоотдачу Q, чтобы поддерживать постоянную температуру.

Работа внешних сил, в нашем случае источника тока, совершаемая над телом при квазистатическом изотермическом процессе, соответствует увеличению свободной энергии тела. Таким образом, формула определяет часть свободной энергии намагниченного вещества, которая обладает связью с магнитным полем:

При малом количестве теплоты Q, относительно энергии поля $E_$ , справедливо равенство:

Согласно условию стабильности магнитной проницаемости вещества, выполняется линейная зависимость:

Выражение применимо при рассмотрении ситуаций в условиях вакуума для парамагнетиков и диамагнетиков. Но при опытах с ферромагнетиками магнитная индукция и напряженность магнитного поля связаны нелинейно, даже при T=const.

Чему равна энергия, как найти, формула

Согласно закону сохранения энергии, вся энергия магнитного поля по итогам опыта преобразиться в Джоулево тепло на сопротивлении R. Величину уменьшения энергии магнитного поля определяют в виде работы индукционного тока:

Результирующие значение силы тока, индукции магнитного поля и энергии равны нулю. Можно принять начальную величину энергии за $E_$ и записать, что:

Элементарная работа, которую совершает ток, вычисляется, таким образом:

$dA_=\varepsilon _Idt=-LI\fracdt=-LIdI$

Здесь dt — время, в течение которого совершается работа током индукции; $\varepsilon _=-L\frac$ — ЭДС самоиндукции.

В связи с изменением тока от I до 0, получим:

Записанная формула справедлива для любого контура и определяет, каким образом связаны энергия магнитного поля, сила тока и индуктивность контура. Можно сопоставить выражение с уравнением кинетической энергии поступательного движения:

Данное соотношение демонстрирует связь индуктивности контура с его инерционностью. Если тело совершает движение, то его невозможно остановить без энергетических превращений. По тому же принципу, нельзя прекратить электрический ток без трансформации энергии.

Читайте также: