Как определяется расстояние между параллельными плоскостями кратко

Обновлено: 05.07.2024

С помощю этого онлайн калькулятора можно найти расстояние между плоскостями. Дается подробное решение с пояснениями. Для нахождения расстояния между плоскостями, введите элементы уравнения плоскости в ячейки и нажимайте на кнопку "Решить".

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Расстояние между плоскостями − теория

Заметим, сначала, что расстояние между плоскостями определена, если плоскости параллельны или, что то же самое, нормальные векторы этих плоскостей коллинеарны. Вычисление расстояния между двумя плоскостями можно свести к вычислению расстояния от точки первой плоскости до второй плоскости. Вычисление расстояния от точки до плоскости (онлайн калькулятор, теория, примеры) посмотрите на странице Расстояние от точки до плоскости онлайн.

Алгоритм вычисления расстояния между плоскостями содержит следующие шаги:

Проверка коллинеарности нормальных векторов плоскостей.
Нахождение некоторой точки M₀ на первой плоскости.
Вычисление расстояния между точкой M₀ и второй плоскостью.

Выведем формулу вычисления расстояния между плоскостями.

Запишем уравнения двух плоскостей:

A₁x+B₁y+C₁z+D₁=0

(1)

A₂x+B₂y+C₂z+D₂=0

(2)

1. Проверяем коллинеарность нормальных векторов n₁=(A₁, B₁, C₁) и n₂=(A₂, B₂, C₂).

Очевидно, что нормальные векторы n₁ и n₂ не могут быть нулевыми векторами.Если из пары коэффициентов (A₁,A₂),(B₁,B₂), (C₁,C₂) один нулевой а другой − нет, то нормальные векторы n₁ и n₂ неколлинеарны. Т.е. задача неразрешима.

Пусть A₁≠0, A₂≠0. Уравнение плоскости (2) не изменится, если умножим на A₁/A₂:

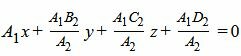(2')

Нормальный вектор уравнения (2') имеет следующий вид:

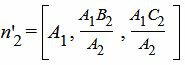Для коллинеарности векторов n₁ и n'₂(или n₁ и n₂) необходимо и достаточно выполнение следующих равенств:

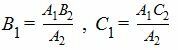(3)

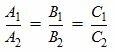(3')

Если удовлетворяется условие (3) (или (3')), то векторы n₁ и n'₂(или n₁ и n₂) коллинеарны, т.е. плоскости (1) и (2') (или (1) и (2) ) параллельны. Тогда уравнение плоскости (2') можно представить так:

A₁x+B₁y+C₁z+D'₂=0

(2'')

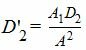2. Найдем некоторую точку на плоскости (1).

Легко убедится, что точка

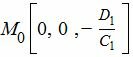(4)

принадлежит плоскости (1):

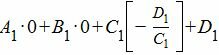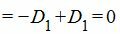3. Расстояние от точки M₀(x₀, y₀, z₀) до плоскости (2'') вычисляется с помощью выражения (подробнее смотрите на странице расстояние от точки до плоскости):

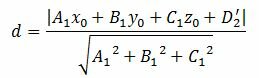(5)

Подставляя координаты точки M₀ из (4) в (5), получим формулу вычисления расстояния между плоскостями (1) и (2'') (или (1) и (2)):

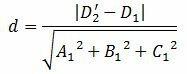(6)

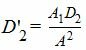Расстояние между плоскостями − примеры и решения

Пример 1. Найти расстояние между плоскостями

(7)

(8)

Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 1/3.

(8')

Общее уравнение плоскости имеет вид:

где n=(A,B,C)− называется нормальным вектором плоскости.

Нормальный вектор плоскости (7) равен n₁=(1, 2, −4), нормальный вектор плоскости (8') равен n₂=(1, 2, −4). n₁=n₂. Следовательно эти плоскости параллельны.

Найдем расстояние между плоскостями (7) и (8'), используя следующую формулу:

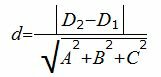(9)

Подставим значения A, B, C, D₁, D₂ в (9):

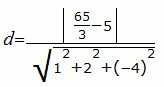Упростим и решим:

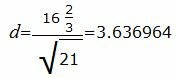Ответ. Расстояние между плоскостями равен:

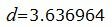Пример 2. Найти расстояние между плоскостями

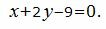(10)

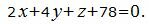(11)

Эти плоскости не параллельны, так как коэффициент переменного z уравнения (10) нулевой а коэффициент переменного z уравнения (11)−нет. Невозможно найти расстояние между непараллельными плоскостями.

Пример 3. Найти расстояние между плоскостями

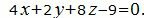(12)

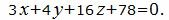(13)

Проверим, являются ли эти плоскости параллельными. Для этого умножим второе уравнение на 4/3.

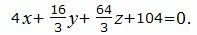(13')

Нормальный вектор плоскости (12) равен n₁=(4, 2, 8), нормальный вектор плоскости (13') равен n₂=(4, 16/3, 64/3). n₁≠n₂. Нормальные векторы этих плоскостей неколлинеарны. Тогда эти плоскости не параллельны и, следовательно, задача неразрешима.

Определение. Расстояние между плоскостями — равно длине перпендикуляра, опущенного с одной плоскости на другую.

Формула для вычисления расстояния между плоскостями

Если заданы уравнения параллельных плоскостей A x + B y + C z + D₁ = 0 и A x + B y + C z + D₂ = 0, то расстояние между плоскостями можно найти, используя следующую формулу

Примеры задач на вычисление расстояния между плоскостями

Решение. Проверим, параллельны ли плоскости, для этого умножим уравнение второй плоскости на 2

2 x + 4 y - 4 z + 18 = 0

Так как коэффициенты при неизвестных величинах у полученного уравнения и первого уравнения равны, то для вычисления расстояния между плоскостями можно использовати приведенную выше формулу:

d =	\|18 - (-6)\|	=	\|24\|	=	24	= 4
	√ 2 2 + 4 2 + (-4) 2		√ 36		6

Ответ: расстояние между плоскостями равно 4.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Устал от плоскостей? Все кажется двумерным и скучным?

Выход есть – попробуй стереометрию!

Так, ладно, хватит говорить, как человек из рекламы.

В этой статье ты научишься одной важной вещи – находить расстояние между плоскостями. Это умение поможет тебе в решении множества задач по стереометрии.

Определение расстояния между параллельными плоскостями

Расстояние между параллельными плоскостями – длина отрезка их общего перпендикуляра, заключенного между плоскостями

\( \displaystyle AB\) – расстояние между плоскостями.

Да, но как найти это расстояние в задачах?

Иногда бывает так, что по каким-то соображениям можно прямо увидеть этот общий перпендикуляр.

Решение задачи №1

Решаем:

Проведем диагональ куба \( \displaystyle A_>\).

1) \( \displaystyle C_>\bot ABCD\rightarrow AC\) – проекция \( \displaystyle A_>\) на \( \displaystyle ABCD\).

\( \displaystyle AC\bot BD\) т.к. (\( \displaystyle ABCD\) – квадрат), значит (Внимание!) по теореме о трех перпендикулярах \( \displaystyle A_>\bot BD\)

Теперь нужно найти \( \displaystyle KM\) — и все!

Нарисуем теперь плоскость \( \displaystyle A>_>C\) отдельно.

Посмотри внимательно и убедись, что чертеж именно такой! А теперь уже легко:

Не очень–то просто?

Но иногда бывает еще хуже: общего перпендикуляра не видно. Нельзя сказать: вот эта линия перпендикулярна обеим плоскостям. Что же тогда делать?

Для того, чтобы найти расстояние между параллельными плоскостями, часто нужно подобрать удобную точку на одной плоскости и найти расстояние от этой точки до другой плоскости.

Решение задачи №2

В правильной шестиугольной пирамиде \( \displaystyle SABCDEF\) точки \( \displaystyle M\) и \( \displaystyle N\) — середины ребер \( \displaystyle SD\) и \( \displaystyle SE\) соответственно.

Найти расстояние между плоскостями \( \displaystyle MNC\) и \( \displaystyle SAB\), если сторона основания пирамиды равна \( \displaystyle 1\), а боковое ребро равно \( \displaystyle 2\).

\( \displaystyle CF||MN\Rightarrow \) точка \( \displaystyle F\in CMN\) и \( \displaystyle CMNF\) – трапеция.

Какая же удобная точка?

Вот представь себе – это точка \( \displaystyle O\)!

Ну, во первых она лежит на плоскости \( \displaystyle CMN\) — это уже хорошо. А во-вторых из нее удобно опускать перпендикуляр на плоскость \( \displaystyle SAB\). Давай увидим это:

Пусть \( \displaystyle K\) – середина \( \displaystyle AB\).

Тогда \( \displaystyle SK\bot AB\) и \( \displaystyle OK\bot AB\).

Значит \( \displaystyle AB\bot SOK\)

Опустим \( \displaystyle OH\) – высоту в \( \displaystyle \Delta SOK\)

Тогда \( \displaystyle OH\bot SK\) – по построению и \( \displaystyle OH\bot AB\), т.к. \( \displaystyle AB\bot SOK\) \( \displaystyle \rightarrow OH\bot SAB\).

Значит, \( \displaystyle OH\) и есть расстояние между \( \displaystyle SAB\) и \( \displaystyle CMN\).

Осталось это \( \displaystyle OH\) найти.

\( \displaystyle OA=OB=AB=1\Rightarrow OK=1\cdot \sin 60<>^\circ =\frac>\)

\( \displaystyle S^>+1=4\Rightarrow S^>=3\); \( \displaystyle SO=\sqrt\).

\( \displaystyle S^>+O^>=S^>\left( \Delta SOK \right)\Rightarrow \)

\( \displaystyle \Rightarrow 3+\frac=S^>\); \( \displaystyle SK=\frac>\)

\( \displaystyle OH=\frac\) (высота прямоугольного треугольника)

Ответ: \( \displaystyle \sqrt>\)

КОРОТКО О ГЛАВНОМ

Расстояние между параллельными плоскостями – длина отрезка их общего перпендикуляра, заключенного между плоскостями

Знаешь геометрический смысл определителя?
Если да, то можно достаточно простым способом через объем параллелепипеда и площадь его грани расстояние посчитать.

PS. Начерталка - тогда я спать.

Мы постоянно добавляем новый функционал в основной интерфейс проекта. К сожалению, старые браузеры не в состоянии качественно работать с современными программными продуктами. Для корректной работы используйте последние версии браузеров Chrome, Mozilla Firefox, Opera, Microsoft Edge или установите браузер Atom.

Читайте также: