Что такое ротор в физике кратко

Обновлено: 05.07.2024

Известная также, как векторный анализ. А кому-то векторный анализ, известный как теория поля =) Наконец-то мы добрались до этой интереснейшей темы! Данный раздел высшей математики язык не поворачивается назвать простым, однако ж, в грядущих статьях я постараюсь достигнуть двух целей:

а) чтобы все понимали, о чём вообще идёт разговор;

Весь материал будет изложен в популярном стиле, и если вам нужна более строгая и полная информация, то можно взять, например, 3-й том Фихтенгольца или заглянуть в Вики.

Поле с травой, футбольное поле…. Ещё? Поле деятельности, поле экспериментов. Приветствую гуманитариев! …Из школьного курса? Электрическое поле, магнитное, электромагнитное…, так, хорошо. Гравитационное поле Земли, в котором мы находимся. Отлично! Так, кто это там сказал о поле действительных и комплексных чисел? …совсем какие-то монстры здесь собрались! =) Благо, алгебра уже пройдена.

На ближайших уроках мы познакомимся со специфическим понятием поля, конкретными примерами из жизни, а также научимся решать тематические задачи векторного анализа. Теорию поля лучше всего изучать, как вы правильно догадываетесь, на поле – природе, где есть лес, речка, озеро, деревенский домик, и я приглашаю всех погрузиться если и не в тёплую летнюю реальность, то в приятные воспоминания:

Во-первых, скаляр. Довольно-таки часто этот термин ошибочно отождествляют с числом. Нет, всё обстоит немного не так: скаляр – это величина, каждое значение которой может быть выражено лишь одним числом. В физике примеров масса: длина, ширина, площадь, объём, плотность, температура и др. Всё это скалярные величины. И, кстати, масса – тоже пример.

Во-вторых, вектор. Алгебраического определения вектора я коснулся на уроке о линейных преобразованиях и одну из его частных ипостасей не знать просто невозможно =) Типичный вектор выражается двумя или бОльшим количеством чисел (своими координатами). И даже для одномерного вектора лишь одного числа не достаточно – по той причине, что у вектора есть ещё направление. И точка приложения, если вектор не свободен. Векторами характеризуют силовые физические поля, скорость и многие другие величины.

Ну что же, теперь можно приступить к сбору ~~алюминиевых огурцов~~ урожая:

Скалярное поле

Если каждой точке некоторой области пространства поставлено в соответствие определённое число (чаще действительное), то говорят, что в этой области задано скалярное поле.

Рассмотрим, например, исходящий из земли перпендикулярный луч. Воткните для наглядности лопату =) Какие скалярные поля можно задать на этом луче? Первое, что напрашивается – это поле высоты – когда каждой точке луча поставлена в соответствие её высота над уровнем земли. Или, например, поле атмосферного давления – здесь каждой точке луча соответствует числовое значение атмосферного давления в данной точке.

Важнейшим свойством скалярного поля является его инвариантность относительно системы координат. Если перевести на человеческий язык, то с какой бы стороны мы на лопату / озеро ни посмотрели – скалярное поле (высота, глубина, температура и т.д.) от этого не изменятся. Более того, скалярное поле, скажем, глубины можно ведь задать и на другой поверхности, например, на подходящей полусфере, или непосредственно на самой водной поверхности. А почему нет? Разве нельзя каждой точке полусферы, расположенной над озером, поставить в соответствие число? Плоскость я предложил исключительно ради удобства.

Добавим ещё одну координату. Возьмите в руку камень. Каждой точке этого камня можно поставить в соответствие его физическую плотность. И опять – в какой бы системе координат мы его ни рассмотрели, как бы ни крутили в руке – скалярное поле плотности останется неизменным. Впрочем, некоторые люди могут оспорить этот факт =) Такой вот философский камень.

Надо сказать, ловким получился переход к следующему параграфу:

Векторное поле

Если каждой точке некоторой области пространства поставлен в соответствие вектор с началом в данной точке, то говорят, что в этой области задано векторное поле.

Большую группу векторных полей образуют так называемые поля скоростей. Посмотрите на поле (которое с травкой) и мысленно очертите над ним произвольную пространственную область. Представьте, что над полем дует ветер – небольшой такой ураганчик для пущей наглядности. Теперь зафиксируем некоторый момент времени и каждой точке построенной области поставим в соответствие несвободный вектор, который характеризует:

а) направление движения воздуха в данной точке;
б) и скорость его движения в данной точке – чем выше скорость, тем длиннее вектор. Если в какой-то точке штиль, то ей сопоставляется нулевой вектор.

Множество этих векторов и образует векторное поле скорости ветра в данный момент времени.

Аналогично устроено поле скоростей течения жидкости – так, например, каждой точке реки в некоторый момент времени можно поставить в соответствие вектор, указывающий направление и скорость течения жидкости в этой точке.

Да чего там ветер и река, поле скорости можно смоделировать собственноручно, для этого достаточно взмахнуть рукой. Или даже моргнуть глазом.

* Далее по умолчанию считаем, что все дела происходят в декартовой системе координат

! Обозначения: векторные поля также обозначают буквой либо , а их компоненты через либо соответственно.

Из вышесказанного давно и очевидно следует, что, по меньшей мере математически, скалярные и векторные поля можно определить и во всём пространстве. Однако с соответствующими физическими примерами я всё же поостерёгся, поскольку таких понятий, как температура, гравитация (или других) ведь где-то может и вовсе не существовать. Но это уже не ужасы, а научная фантастика =) И не только фантастика. Ибо внутри камней ветер, как правило, не дует.

Векторные линии

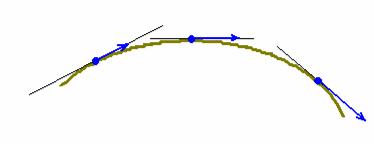
Постараюсь сформулировать попроще: каждая точка векторной линии является началом вектора поля, который лежит на касательной в данной точке:

Разумеется, векторы линии в общем случае имеют разную длину, так на приведённом рисунке, при перемещении слева направо их длина растёт – здесь можно предположить, что мы приближаемся, например, к магниту. В силовых физических полях векторные линии так и называют – силовыми линиями. Другой, более простой пример – это гравитационное поле Земли: его силовые линии представляют собой лучи с началом в центре планеты, причём векторы силы тяжести расположены прямо на самих лучах.

Векторные линии скоростных полей называются линями тока. Множество линий тока даёт нам представление о потоке жидкости или газа в данный момент времени. К слову, линия тока и траектория движения частицы – это не одно и то же. Если поле скоростей не меняется с течением времени (например, река с устоявшимся течением), то, да – мусоринки будут плыть по линиям тока. Такое поле называют стационарным, и в нём траектории движения частиц совпадают с линиями тока. Но представьте пыльную бурю – здесь линии тока в каждый момент разные, и поэтому мусоринка будет лететь по своей уникальной траектории, а вовсе не по какой-то конкретной линии тока.

Вообще, многие понятия теории поля пришли из гидродинамики, с чем мы ещё не раз столкнёмся.

если , то нужно решить систему ;
если , то систему ;
и если , то .

И что-то непозволительно давно у нас не было практики:

Найти силовые линии векторного поля

Решение: в данной задаче , поэтому решаем систему:

Первый диффур вообще халява:

– семейство плоскостей, параллельных координатной плоскости (представили в уме!).

Второй диффур – почти она же:), ну а зачем нам скоропостижные трудности?

– семейство (внимание!) параболических цилиндров, параллельных оси .

Ответ: искомое множество векторных линий:

Аналогичная задачка для самостоятельного решения:

Найти силовые линии векторного поля

Охарактеризуйте получившееся множество линий. Кстати, в условии явно не сказано, о каком поле идёт речь – плоском или пространственном. В подобных ситуациях рекомендую решать задачу для пространства – не ошибётесь ;-)

Краткое решение и ответ в конце урока.

Векторное поле градиентов

В каких отношениях вы находитесь с производной по направлению и градиентом? …ничего страшного, от ненависти до любви – один шаг =) Напоминаю, что градиент функции в точке – это несвободный вектор, указывающий направление максимального роста функции в данной точке и определяющий скорость этого роста.

Нахождение векторной функции градиентов – есть популярный и распространённый способ получить из скалярного поля поле векторное. При условии существования соответствующих частных производных функции двух и трёх переменных:

Смысл очень прост. Так, если функция задаёт скалярное поле глубины озера, то соответствующая векторная функция определяет множество несвободных векторов, каждый из которых указывает направление наискорейшего подъёма дна в той или иной точке и скорость этого подъёма.

Если функция задаёт скалярное поле температуры некоторой области пространства, то соответствующее векторное поле характеризует направление и скорость наибыстрейшего прогревания пространства в каждой точке этой области.

Разберём общую математическую задачу:

Дано скалярное поле и точка . Требуется:

1) составить градиентную функцию скалярного поля;

2) найти градиент поля в точке и вычислить его длину;

3) вычислить производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.

Непосредственно к решению задачи это не относится, но сразу обратим внимание, что скалярное поле не определено на всех трёх координатных плоскостях .

1) Быстренько вспоминаем, как находить частные производные функции трёх переменных:

Составим функцию, которая определяет векторное поле градиентов:

И ещё раз – в чём её смысл? Полученная векторная функция каждой точке области определения скалярного поля ставит в соответствие вектор , указывающий направление и максимальную скорость роста функции в данной точке.

И один из таких векторов нам предстоит найти в следующем пункте:

2) Вычислим частные производные в точке :

Мерилом же этой максимальной скорости как раз является длина градиента:

3) Вычислим производную по направлению нормального вектора к поверхности в точке , образующего с положительной полуосью тупой угол.

Получено верное равенство. ОК.

Что это за поверхность – нас не интересует, нам важен её нормальный вектор в точке , да не абы какой, а образующий с полуосью тупой угол.

Вспоминаем материал ещё одного урока: вектор нормали к поверхности в точке задаётся следующим образом:

В данном случае:

, следовательно, угол между этими векторами острый, что нас не устраивает!

И поэтому нужно выбрать противоположно направленный нормальный вектор:

Заметим заодно, что нормальные векторы в отличие от градиентов – свободны, их задача лишь указать направление.

Вычислим направляющие косинусы данного направления, или, что то же самое – координаты единичного вектора, сонаправленного с вектором :

Таким образом, искомая производная по направлению:

Напоминаю, что это значение характеризует скорость роста функции в точке по направлению вектора , и оно не может оказаться больше, чем (максимальной скорости роста в данной точке).

Ответ:

Небольшой пример для самостоятельного решения:

Найти угол между градиентами скалярных полей и в точке

Потенциальное векторное поле

В физике есть конкретная математическая модель, описывающая гравитационные силы, но в соответствии с направленностью сайта, я приведу только общие формулы. Итак:

Векторное поле является потенциальным, если оно представляет собой поле градиентов некоторого скалярного поля . Функцию называют потенциальной функцией или просто потенциалом.

Работа потенциального векторного поля по перемещению материальной точки из точки в точку не зависит от траектории её движения и выражается следующим криволинейным интегралом 2-го рода:

, который равен разности потенциалов .

Иными словами, в потенциальном поле имеет значение лишь начальная и конечная точка маршрута. И если эти точки совпадают, то суммарная работа сил по замкнутому контуру будет равна нулю:

Давайте поднимем пёрышко с земли и доставим его в исходную точку. При этом траектория нашего движения опять же произвольная; можно даже бросить перо, снова его поднять и т.д.

Почему итоговый результат нулевой?

Таким образом, суммарная работа сил равна нулю:

Как я уже отмечал, физическое и обывательское понятие работы отличаются. И это различие вам хорошо поможет понять не пёрышко и даже не кирпич, а, например, пианино :)

Дружно поднимите пианино и спустите его по лестнице вниз. Потаскайте по улице. Сколько захочется и где захочется. И ~~если никто не вызвал дурку~~ занесите инструмент обратно. Вы поработали? Конечно. До седьмого пота. Но с точки зрения физики никакой работы не совершено.

Ротор векторного поля

Или его вихревая составляющая, которая тоже выражается векторами.

Снова возьмём в руки пёрышко и аккуратно отправим его в плавание по реке. Для чистоты эксперимента будем считать, что оно однородно и симметрично относительно своего центра. Ось торчит вверх.

Рассмотрим векторное поле скорости течения (считаем, что оно неизменно во времени), и некоторую точку водной поверхности, над которой находится центр пера.

Если векторное поле задано функцией , то его роторное поле задаётся следующей векторной функцией:

И, наконец, отвечаем на поставленный выше вопрос: в любой точке потенциального поля его ротор равен нулю:

, а точнее, нулевому вектору.

Потенциальное поле также называют безвихревым полем.

После чего с чистой совестью и повышенным тонусом можно вернуться к практическим задачам:

Показать, что векторное поле является потенциальным и найти его потенциал

Решение: условие прямо утверждает потенциальность поля, и наша задача состоит в доказательстве этого факта. Найдём роторную функцию или, как чаще говорят – ротор данного поля:

Для удобства выпишем компоненты поля:

Таким образом:
, следовательно, поле потенциально, а значит, представляет собой градиентную функцию некоторого скалярного поля, заданного потенциалом .

Функцию обычно находят одним из следующих способов:

1) Способ первый. Коль скоро так (см. выше), то:

Дальнейший алгоритм напоминает решение дифференциального уравнения в полных дифференциалах, только с бОльшим количеством шагов:

Но, с другой стороны . Приравниваем и упрощаем:

Но с другой стороны, . Приравниваем и упрощаем:

– получаем тем самым, искомую потенциальную функцию.

Проверку тут выполнить легче лёгкого, находим частные производные 1-го порядка:

которые совпали с соответствующими компонентами исходного поля , в чём и требовалось убедиться.

2) Способ второй. Потенциальную функцию можно найти при помощи формулы:
, где – точка с переменными координатами, а – некоторая фиксированная точка скалярного поля .

Легко видеть, что этот криволинейный интеграл определяет работу векторного поля от точки до точки и численно равен разности потенциалов , откуда, собственно, и получается нужная функция

Запишем сумму трёх интегралов для поля :

И на этом шаге я по возможности рекомендую выбрать точку (если функция и её производные в ней определены). После чего решение значительно упрощается:

Ответ:

Если начало координат выбрать нельзя, то задачу придётся решать в общем виде, в результате чего должна получиться разность . Любители трудностей могут вернуться к примеру и прийти к разности . Разумеется, это легальный и рабочий вариант – можно решать и так.

Пара полей для самостоятельного решения:

Выяснить, является ли следующие векторные поля потенциальными, и если да, то найти их потенциалы:

Обязано ли поле быть потенциальным в таких задачах? Конечно, нет, и отрицательный ответ – это тоже полноценный ответ. Примерный образец чистового оформления заданий внизу страницы.

Ну что же, теперь пришло время немного отдохнуть и увеличить ротор реки =) А именно нырнуть, искупаться и позагорать на солнце. Чтобы с новыми силами вернуться к столь увлекательной теме, а именно к потоку и циркуляции векторного поля

Спасибо за внимание и до скорых встреч!

Решения и ответы:

Пример 2: Решение: составим и решим систему:

Из 1-го уравнения:

Из 2-го уравнения:

Константу переобозначим через

Ответ: – семейства эллипсов, расположенные в плоскостях , параллельных плоскости .

Пример 4: Решение: вычислим частные производные функции в точке :

Составим градиент данного скалярного поля в точке и вычислим его длину:

Аналогично найдём градиент второго скалярного поля:

В результате:

Угол между градиентами найдём по формуле:

Таким образом:

Пример 6: Решение:

а) проверим, равен ли нулю ротор векторного поля:
.
В данном случае:

Следовательно,

Ответ: поле не потенциально.

Ответ: поле потенциально,

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

(от лат. roto - вращаю) (вихрь) - одна из осн. операций векторногоанализа, сопоставляющая векторному полю а(r )др. векторное полеrot а (используются также обозначения curl а). Если точка r задана своими декартовыми координатами,а вектор а - своими компонентами, то rot a имеет компоненты

Согласно Стокса формуле. Р.векторного поля определяет его циркуляцию вдоль произвольной замкнутой кривой. Если а - распределение скоростейв движущейся жидкости, то значение вектора rot а в каждой точке совпадаетс вектором угл. скорости вращения бесконечно малого элемента жидкости, след. свойствами:

Если rot а= 0, то векторное поле а наз. безвихревым илипотенциальным. В этом случае существует скалярное поле (потенциал поля а), такое, что его можно выразить через объёмный интеграл где г - расстояние от элемента объёма dV до точки, в к-рой разыскиваетсязначение поля . м.

Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия . Главный редактор А. М. Прохоров . 1988 .

Ротор (Вихрь) — векторный оператор векторного поля, показывает насколько и в какую сторону закручено поле в каждой точке. Ротор обозначается значком rot или :

$<\displaystyle \nabla \times F> $
, где

$<\displaystyle \nabla > $
векторный дифференциальный оператор набла, и F изучаемое векторное поле. В декартовой системе координат

$<\displaystyle \nabla \times F> $
вычисляется следующим образом:

$<\displaystyle <\rm <rot> >(>F_+>F_+>F_)=>\left(<\frac <\partial F_><\partial y>>-<\frac <\partial F_><\partial z>>\right)+>\left(<\frac <\partial F_><\partial z>>-<\frac <\partial F_><\partial x>>\right)+>\left(<\frac <\partial F_><\partial x>>-<\frac <\partial F_><\partial y>>\right)>$

Для простоты восприятия можно представлять ротор как

$<\displaystyle <\begin <\partial x>>\\\\<\partial y>>\\\\<\partial z>>\end>\times F>$

Или как детерминант следующей матрицы:

$<\displaystyle <\begin \mathbf &\mathbf &\mathbf \\\\<\partial x>>&<\partial y>>&<\partial z>>\\\\F_&F_&F_\end>>$

где i, j и k — единичные векторы для осей x, y и z соответственно.

Векторное поле, ротор которого равен нулю в любой точке, называется Физическая интерпретация

Например, если в качестве векторного поля взять поле скоростей ветра на Земле, то для по часовой стрелке , ротор будет направлен вниз, а для циклона, вращающегося против часовой стрелки — вверх. В тех местах, где ветры дуют равномерно и прямолинейно, ротор будет равен нулю.

Основные свойства

Следующие свойства могут быть получены из обычных правил дифференцирования.

для любых векторных полей F и G и для всех действительных чисел a и b.

Если φ — скалярное поле, а F — векторное, тогда:

$<\displaystyle \nabla \times (\varphi \mathbf )=(\nabla \varphi )\times \mathbf +\varphi \;(\nabla \times \mathbf ).>$

$<\displaystyle \nabla \cdot (\nabla \times \mathbf <F> )=0>$

Ротор – важная составляющая многих машин и механизмов. Наиболее важной деталью, обозначаемой при помощи данного понятия, является так называемый якорь электрического двигателя, генераторов переменного тока. Равно как и колесо, изобретение и использование ротора позволили сделать человечеству огромный шаг навстречу электрификации. Более подробно о том, что такое ротор, в каких механизмах и машинах он применяется, каких видов бывает, будет рассказано в этой статье.

Определение

С точки зрения электротехники, классический ротор – это вращающееся цилиндрическое тело, имеющее следующее строение:

Вал из прочной инструментальной стали с как минимум двумя подшипниками, расположенными по одному в передней и задней частях;
Сердечники из толстых металлических пластин;
Намотанные на собранные из пластин сердечники катушки;
Коллектор или пара специальных токопроводящих колец.

Для принудительного воздушного охлаждения вращающейся очень часто с большой скоростью детали служит расположенная в одном из его торцов крыльчатка. В генераторах вращение ротору передается от турбины, соединенной с ним через общий вал, или от работающего двигателя при помощи шкива, на который одет гибкий и прочный ремень (клинно-ременная передача).

Так, основная функция ротора – это вращение относительно неподвижной части. В электротехнике такой неподвижной частью является статор. Вместе ротор и статор являются важнейшими составляющими электродвигателей и генераторов переменного тока.

Связанные определения

Векторное поле, ротор которого равен нулю в любой точке, называется безвихревым

и является
потенциальным
. Поскольку эти условия являются друг для друга необходимыми и достаточными, оба термина являются практическими синонимами. (Впрочем, это верно только для случая полей, определённых на односвязной области).

Чуть подробнее о взаимной обусловленности потенциальности и безвихревого характера поля — см. ниже (Основные свойства).

Напротив, поле, ротор которого не равен нулю, называется обычно вихревым

, такое поле не может быть потенциальным.

Виды электромеханических устройств

Статор — понятие и принцип действия

Используют ротор в таких электромеханических устройствах, как двигатели, работающие на постоянном и переменном электрическом токе, генераторы.

Агрегаты, работающие на переменном токе

К таким агрегатам относятся различные электродвигатели. Наиболее распространенная модель данного устройства состоит из следующих частей:

Алюминиевый или чугунный ребристый корпус с монтажной коробкой для подключения обмоток статора и ротора;
Статор – неподвижная часть в виде полого цилиндра, расположенная внутри корпуса. Обмотка статора состоит из 3 пар расположенных друг напротив друга намотанных в пазы корпуса катушек из медного изолированного провода
Цельнометаллический цилиндрический ротор с валом и пазами, в которые впаяны обладающие высокой токопроводящей способностью алюминиевые стержни.

Двигатель, запитываемый от переменного тока

Вращается ротор на двух опорных подшипниках, запрессованных на его валу. Охлаждение работающего на больших оборотах электродвигателя происходит, благодаря крыльчатке – небольшому вентилятору, состоящему из множества лопастей и расположенному на одном из концов вала ротора. Также эффективному охлаждению работающего агрегата способствует ребристая структура алюминиевого корпуса.

Принцип работы подобного двигателя заключается в следующем:

При подключении тока к агрегату он попеременно проходит через одну из трех пар катушек статора.
При протекании по парам статорных катушек электрического тока они создают магнитное поле, силовые линии которого пересекают ротор.
Попеременно запитываемые пары катушек создают подвижное магнитное поле, которое по закону электромагнитной индукции провоцирует появление в неподвижных металлических стержнях ротора электрического тока.
Индуцированный ток в роторе приводит к появлению силы, выталкивающей его из магнитного поля статора. Так как частота подачи тока на катушки статора в среднем составляет порядка 30 импульсов в секунду, появившаяся в роторе выталкивающая сила приводит к его вращению с большой скоростью.

Важно! В зависимости от одновременности вращения ротора и порождающего это движение магнитного поля электрический двигатель переменного тока может быть синхронный (ротор агрегата вращается синхронно с магнитным полем статора) и асинхронный (вращение якоря не синхронизировано с движением магнитного поля статора). Первый вид отличается высокой мощностью и надежностью, в то время как второй характеризуется большим разнообразием конструкций и областей применения.

Машины постоянного тока

Наиболее распространенный электродвигатель постоянного тока щеточного вида представляет собой электрический агрегат, состоящий из:

Чугунного корпуса с ребрами охлаждения и специальным монтажным коробом для подключения обмоток агрегата;
Вала из прочной инструментальной стали с двумя подшипниками;
Якоря, состоящего из сердечника (набора пластин из специальной электротехнической стали), якорной обмотки (размещенных в пазах сердечника катушек из медного провода);
Индуктора, состоящего из полюсов возбуждения с намотанными на них катушками из медного провода;
Коллектора – расположенных на валу медных пластин, к которым подключаются выводы катушек якорной обмотки;
Подпружиненных графитовых или металлографитовых щеток (щеточной группы).

Охлаждается такой двигатель, как и аналог, работающий от переменного тока, – расположенной на валу крыльчаткой.

Двигатель, работающий от постоянного тока

Важно! В отличие от электродвигателя переменного тока частотой вращения ротора в таком силовом агрегате управляет специальный блок, который при помощи установленного на валу датчика Холла определяет положение ротора и его скорость.

Работает подобный агрегат следующим образом:

Останавливают вращение такого агрегата прекращением подачи напряжения на щеточную группу.

Помимо описанных выше электромоторов, к машинам, работающим на постоянном токе, относится также роторный стартер – устройство, необходимое для запуска бензиновых и дизельных автомобильных двигателей внутреннего сгорания.

Ротор векторного поля. Формула Стокса

Ротор поля. Формула Стокса

Ротором (или вихрем) векторного поля
называется вектор, обозначаемый

и определяемый формулой

Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:

Отметим некоторые свойства ротора.

Если — постоянный вектор, то .
, где .
, т. e. ротор суммы двух векторов равен сумме роторов слагаемых.
Если — скалярная функция, а — векторная, то

Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:

Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:

Левая часть формулы (71.14) представляет собой циркуляцию вектора

по контуру , т. е. (см. (71.11)). Интеграл в правой части формулы (71.14) представляет собой поток вектора через поверхность , ограниченную контуром (см. (71.3)), т. е.

Следовательно, формулу Стокса можно записать в виде

Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре

и выбор стороны у поверхности согласованы между собой так же, как в теореме Стокса.

Формула (71.15) показывает, что циркуляция вектора

вдоль замкнутого контура равна потоку ротора этого вектора через поверхность , лежащую в поле вектора и ограниченную контуром (натянутую на контур) (см. рис. 278).

Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.

Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки

с контуром , содержащей точку .

По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:

— некоторая (средняя) точка площадки (см. рис. 279).

Тогда формулу (71.15) можно записать в виде

стягивается в точку . Тогда , a . Перейдя к пределу, получаем:

в точке называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции вектора по контуру плоской площадки , перпендикулярной этому направлению, к площади этой площадки.

Как видно из определения, ротор вектора

есть векторная величина, образующая собственное векторное поле.

Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор ноля линейных скоростей твердого тела, вращающегося вокруг оси

с постоянной угловой скоростью (пример 69.2) , т. е. ротор вектора .

По определению ротора

Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.

С точностью до числового множителя ротор поля скоростей

Замечание. Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке

Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Дивергенция поля. Формула Остроградского-Гаусса

Циркуляция векторного поля

Свойства основных классов векторных полей

Дифференцирование функции комплексного переменного

Типы роторов

Генератор тока переменного

В зависимости от области применения и строения, роторы бывают следующих типов:

Фазный – якоря данного типа представляют собой совокупность намотанных на сердечник катушек, расположенных относительно друг другу под углом 1200. Концы проводов катушек выводятся к пластинам коллектора и запитываются при помощи щёточного узла.
Короткозамкнутый –ротор такого типа состоит из цельного цилиндра с пазами, в которые укладываются стержни из электролитической меди или алюминия. Концы таких стержней соединяются между собой кольцом. Коллектора и щеточного узла в агрегатах, оборудованных подобным якорем, не имеется.

Двигатели с фазным типом якоря отличаются большими размерами и весом, но при этом обладают прекрасным пуском и регулировкой. Агрегаты с короткозамкнутыми роторами имеют меньшие размеры, меньшую подверженность поломкам, простоту в эксплуатации.

Разобравшись в том, что такое собой представляют ротор и статор, можно получить не только полезные теоретические знания, но и практические навыки: зная устройство агрегатов, работающих на постоянном и переменном токе, можно при наличии неисправности проверить работоспособность их основных узлов, определить, виноваты ли в поломке намотка якоря, статор, щеточный или коллекторный узел.

Роторы

Ротор нужен для осуществления вращения бурильной колонны (подвешенной), он также необходим при бурении забойными двигателями (с его помощью осуществляется восприятие реактивного крутящего момента) и при проворачивании инструмента в ходе ловильных работ. Роторы также эффективны при поддержании обсадных труб или бурильных колонн на весу.
Роторы выглядят как конический редуктор с зубцами. Коническое колесо аппарата соединено со столом и насажено на втулку, а ось стола расположена по оси скважины. Ротор так же используют для свинчивания и развинчивания труб.

Ротор — один из основных механизмов буровой установки, поэтому существует несколько его классификаций.

Роторы могут различаться по диаметру проходного отверстия, по мощности и по допускаемой статистической нагрузке

Известна классификация по конструкторской характеристике : роторы неподвижные и перемещающиеся возвратно-поступательно относительно устья скважины. Перемещение происходит в вертикальном направлении.

Важнейшая технологическая компонента ротора — привод. Привод может запускаться посредством:

цепных, карданных и зубчатых передач от буровой лебедки индивидуального двигателя коробки смены передач

Привод ротора обусловливает различное изменение скоростей и моментов вращения. Оно может быть:

ступенчатым непрерывно-ступенчатым непрерывным

В буровых установках привод ротора управляется с помощью цепной трансмиссии от лебедки или КПП карданной передачи. При установке лебедки ниже пола буровой управление осуществляется дополнительной трансмиссией от лебедки.

Состав роторной установки:

Ротор состоит из станины с расточкой для стакана со смонтированным приводным валом. На столе и станине ротора расположены кольцевые проточки. Они образуют лабиринтные уплотнения для защиты масляной ванны от попадания в нее раствора. В станине так же установлен упорный подшипник, а снизу — вспомогательный подшипник. Вспомогательный подшипник ротора предназначен для центрирования стола ротора и восприятия направленных вверх нагрузок. Снизу установлено специальное лабиринтное колесо, предохраняющее попадание раствора в масляную ванну.

В табл. 30 приведена техническая характеристика роторов

На рисунке показан ротор Р-560.

Для них характерны следующие конструкторские новшества:

надежное лабиринтное уплотнение масляной ванны (это повышает эксплуатационный срок зубцов ротора и основной опоры стола)

стопорное устройство способно фиксировать стол (это также это повышает эксплуатационный срок зубцов ротора, продлевает срок службы опор)

зубчатые колеса характеризуются повышенной точностью и плавностью зацепления

Читайте также: