Что такое результат эквивалентности в информатике кратко
Обновлено: 05.07.2024
Логические операции в создании компьютерных программ — действия, которые производятся над входными данными. Такие функции производятся над сигналами булевского типа, то есть над примитивными выражениями, имеющими только два возможных значения: истина или ложь.
Виды операций
В программировании выделяют следующие виды функций:
- Логическое умножение или конъюнкция.
- Логическое сложение или дизъюнкция.
- Логическое отрицание или инверсия.
- Логическое следование или импликация.
- Логическая равнозначность или эквивалентность.
- Стрелка Пирса.
- Штрих Шеффера .
Логическое умножение (конъюнкция)
Конъюнкция — это действие, в результате которого каждым двум входным данным соответствует одно новое высказывание. Истинное значение на выходе получается, когда оба входных значения истинны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Таблица истинности для логического умножения выглядит так:
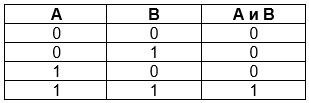
A, B — исходные данные;
A и B — значение, приобретаемое в результате реализации конъюнкции.
Из таблицы следуют свойства логического умножения:
- при ложном значении одной входной информации из двух конъюнкция будет ложной;
- при истинном значении переменных конъюнкция будет истинной;
- результат логического умножения не зависит от порядка записи ее переменных.
Логическое сложение (дизъюнкция)
Дизъюнкция — это булева функция, в итоге которой выходные данные будут ложными только при ложности всех исходных выражений.
Таблица истинности логического сложения:
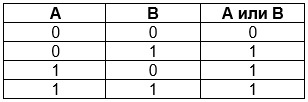
A, B — входная информация;
A или B — значение, приобретаемое в результате выполнения дизъюнкции.
Для дизъюнкции справедливы следующие утверждения:
- при истинности хотя бы одного подвыражения дизъюнкция будет истинной;
- при ложности всех высказываний дизъюнкция примет ложное значение;
- итог дизъюнкции не зависит от перемены мест слагаемых.
Логическое отрицание (инверсия)
Инверсия — выражение, ставящее в соответствие одному значению противоположное.
Таблица истинности инверсии:
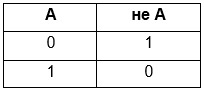
A — исходные данные;
не A — значение, приобретаемое в результате логического отрицания.
Логическое следование (импликация)
Импликация — это булева операция, ложная лишь тогда, когда первая исходная переменная является истиной, а вторая — ложью.
Следование записывается с помощью знака \(\rightarrow.\)
Таблица истинности для импликации:
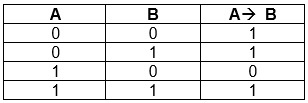
A — входная информация, означающая условие;
B — входная информация, означающая следствие;
A → B — значение, приобретаемое в результате импликации.
Логическая равнозначность (эквивалентность)
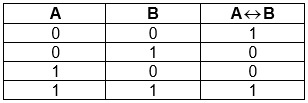
Эквивалентность — выражение, являющееся истинным лишь в случае равенства двух входных элементов.
При записи равнозначности используют стрелки \(\Leftrightarrow\) , \(\leftrightarrow\) , \(\Xi\) .
Таблица истинности для равнозначности:
Стрелка Пирса
Стрелка Пирса — двухместное логическое действие со следующей последовательностью: сначала над исходными показаниями производится дизъюнкция, затем происходит отрицание полученного результата.
Данная манипуляция является отрицание логического сложения. Свое название рассматриваемая функция получила от своего автора — американского ученого Чарльза Пирса.
Запись стрелки Пирса осуществляется через знак \(\downarrow\) .
Таблица истинности для этой операции следующая:
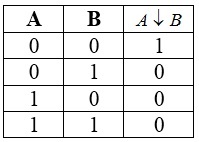
Особенность стрелки Пирса заключается в ее возможности строить другие булевы функции.
Пример
Штрих Шеффера
Штрих Шеффера — это действие, приводящее к ложному итогу лишь при истинности обоих исходных данных. По порядку выполнения операций эта функция эквивалентна отрицанию конъюнкции.
Символ Шеффера назван по фамилии своего создателя — американского логика Генри Шеффера — и обозначается посредством знака \(\vert.\)
Таблица истинности для данной функции:
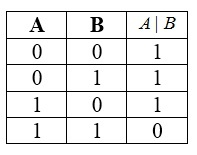
С помощью штриха Шеффера можно воспроизвести другие логические манипуляции.
Пример
Порядок выполнения операций
В составном логическом выражении действия выполняются в такой последовательности:
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквивалентность.
Для построения нужного порядка, как и в математических выражениях, используют скобки.
Тот, кто хочет подробно разбираться в цифровых технологиях должен понимать основы такой темы, как алгебра логики. В этой статье будут разобраны основные определения, а также показаны самые важные логические операции, такие как конъюнкция, дизъюнкция, импликация и т.д.
Основные положения
Для начала следует разобраться, для чего нужна алгебра логики – главным образом, этот раздел математики и информатики, нужен для работы с логическими выражениями и высказываниями.
Логическим высказыванием называется утверждение (или запись), которое мы можем однозначно классифицировать, как истинное или ложное (1 или 0 в информатике).
Примером таким высказываний будут являться:
- Сегодня светит солнце;
- 5 > 3;
- Химическая таблица элементов была разработана Д.И. Менделеевым.
Отсюда можно сделать вывод, что в русском языке логическими высказываниями являются повествовательные предложения, однако далеко не все повествовательные предложения являются логическими высказываниями . Пример: химия скучный предмет. Здесь мы не можем однозначно установить ложно ли это выражение или истинно.
Логические высказывания делятся на два типа — простые и сложные.
- Простые высказывания состоят из одного утверждения, которые мы можем однозначно охарактеризовать, как истинные или ложные.
- Сложные же состоят из нескольких таких утверждений, которые объединены с помощью логических операций (рассмотрены дальше).
В алгебре логики, как простые, так и сложные высказываниями описываются булевыми выражениями.
Булево выражение – это символическое (знаковое) описание высказывания.
В таких выражениях простые высказывания выступают в роли переменных и обозначаются буквами латинского алфавита, а операции обозначаются при помощи специальных знаков . После выполнения всех операций и упрощения выражения мы получаем результат, на основании которого строится таблица истинности.
Операции
Ниже рассмотрим основные операции, которые применяются в булевой алгебре. Их хватит, чтобы упростить львиную долю всех выражений, которые Вам встретятся.
Конъюнкция
Функция может работать как с двумя операндами (высказываниями), так и с тремя, четырьмя и т.д. В математике обозначается с помощью знаков \( \wedge \) и &. Обозначение в языках программирования AND, &&. Таблица истинности для двух операндов:
Дизъюнкция
Булево сложение, также как и умножение, может работать с произвольным количеством операндов. В математике обозначается как V, а в программировании с помощью OR или I.
Инверсия
Логическое отрицание – функция, работающая с одним высказыванием, и заменяющая истину на ложь, а ложь на истину. В математике обозначается с помощью черты над значением, а в программирование и информатике с помощью слова NOT.
Импликация
Результирующее значение будет ложным только тогда, когда из истинного высказывания будет следовать ложное следствие . Имеет обозначение в виде стрелочки \( \Longrightarrow \) . Важно: импликация работает только с двумя операндами.
Эквивалентность
Обозначается с помощью трех черточек или ⟺.
Порядок выполнения операций
Логические операции выполняются в следующем порядке:
- Первой выполняется инверсия переменных.
- Вторым выполняется конъюнкция (булево умножение);
- Третьим номером идет дизъюнкция (сложение);
- Затем выполняется импликация;
- Самым низким приоритетом выполнения обладает эквивалентность.
Если в формуле указаны скобки, то порядок выполнения действий в скобках точно такой же, как написано выше.
Пример
Дано два отрезка B = [2,10], C = [6,14]. Из предложенных вариантов ответа выберите такой отрезок A, что формула \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) истинна при любом значении z. Варианты ответа:
Решение: Подставим в уравнение \( ((z \in A) \Longrightarrow (z \in B)) \vee (z \in C) \) =1 значения B и C и составим таблицу истинности:
Получившаяся формула \( ((z \in A) \Longrightarrow (z \in [2,10])) \vee (z \in [6,14])=1 \). По условию \( z \in A \)=1.
Таблица истинности для всех отрезков:

Ответ: A = [3,11].
Видео
Заключение
Вот Вы и познакомились с основными логическими операциями и понятиями и знаете, что такое булево сложение и умножение. Если вас заинтересовала данная тема, то можете изучить булевы законы. Эти законы не проходятся в рамках школьной программы и служат для упрощения сложных выражений.
Алгебра логики (англ. algebra of logic) — один из основных разделов математической логики, в котором методы алгебры используются в логических преобразованиях.
Современная алгебра логики является разделом математической логики и изучает логические операции над высказываниями с точки зрения их истинностного значения (истина, ложь). Высказывания могут быть истинными, ложными или содержать истину и ложь в разных соотношениях.
Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Логических значений всего два: истина (TRUE) и ложь (FALSE). Это соответствует цифровому представлению — 1 и 0. Результаты каждой логической операции можно записать в виде таблицы. Такие таблицы называют таблицами истинности.
Основные операции алгебры логики
Операция, используемая относительно одной величины, называется унарной. Таблица значений данной операции имеет вид
| A | ¬A |
| истина | ложь |
| ложь | истина |
| A | ¬A |
| 1 | 0 |
| 0 | 1 |
Высказывание $A↖$ ложно, когда А истинно, и истинно, когда А ложно.
Геометрически отрицание можно представить следующим образом: если А — это некоторое множество точек, то $A↖$ — это дополнение множества А, т. е. все точки, которые не принадлежат множеству А.

Таблица истинности операции имеет вид
| A | B | A ∧ B |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∧ B |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∧ В истинно только тогда, когда оба высказывания — А и В истинны.
Геометрически конъюнкцию можно представить следующим образом: если А, В — это некоторые множества точек, то А ∧ В есть пересечение множеств А и В.

Таблица истинности операции имеет вид
| A | B | A ∨ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | истина |
| A | B | A ∨ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
Высказывание А ∨ В ложно только тогда, когда оба высказывания — А и В ложны.
Геометрически логическое сложение можно представить следующим образом: если А, В — это некоторые множества точек, то А ∨ В — это объединение множеств А и В, т. е. фигура, объединяющая и квадрат, и круг.

Таблица истинности операции имеет вид
| А | В | А ⊕ B |
| истина | ложь | истина |
| ложь | истина | истина |
| ложь | ложь | ложь |
| истина | истина | ложь |
| А | В | А ⊕ B |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
| 1 | 1 | 0 |
Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.
Таблица истинности операции имеет вид
| А | В | А → В |
| истина | ложь | ложь |
| ложь | истина | истина |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А → В |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина.
Таблица истинности операции эквивалентности имеет вид
| А | В | А ∼ В |
| истина | ложь | ложь |
| ложь | истина | ложь |
| ложь | ложь | истина |
| истина | истина | истина |
| А | В | А ∼ В |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
Зная значения простых высказываний, можно на основании таблиц истинности определить значения сложных высказываний. При этом важно знать, что для представления любой функции алгебры логики достаточно трех операций: конъюнкции, дизъюнкции и отрицания.
| Сложение по модулю два | А ⊕ В | $(A↖ ∧B) ∧ (A ∧ B↖)$ |
| Импликация | А → В | $A↖ ∨ B$ |
| Эквивалентность | А ∼ В | $(A↖ ∧ B↖) ∨ (A ∧ B)$ |
Примеры решения задач
Пример 1. Определить для указанных значений X значение логического высказывания ((X > 3) ∨ (X 3) ∨ (1 3) ∨ (12 3) ∨ (3 2) → (X > 5)) .
Пример 3. Для каких из приведенных слов ложно высказывание ¬(первая буква гласная ∧ третья буква гласная) ⇔ строка из 4 символов? 1) асса; 2) куку; 3) кукуруза; 4) ошибка; 5) силач.
Решение. Рассмотрим последовательно все предложенные слова:
1) для слова асса получим: ¬(1 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
2) для слова куку получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 1 — высказывание истинно;
3) для слова кукуруза получим: ¬ (0 ∧ 0) ⇔ 0, 1 ⇔ 0 — высказывание ложно;
4) для слова ошибка получим: ¬ (1 ∧ 1) ⇔ 0, 0 ⇔ 0 — высказывание истинно;
5) для слова силач получим: ¬ (0 ∧ 0) ⇔ 1, 1 ⇔ 0 — высказывание ложно.
Логические выражения и их преобразование
Логические выражения могут включать в себя функции, алгебраические операции, операции сравнения и логические операции. В этом случае приоритет выполнения действий следующий:
- вычисление существующих функциональных зависимостей;
- выполнение алгебраических операций (вначале умножение и деление, затем вычитание и сложение);
- выполнение операций сравнения (в произвольном порядке);
- выполнение логических операций (вначале операции отрицания, затем операции логического умножения, логического сложения, последними выполняются операции импликации и эквивалентности).
В логическом выражении могут использоваться скобки, которые изменяют порядок выполнения операций.
Пример. Найти значение выражения:
$1 ≤ a ∨ A ∨ sin(π/a - π/b) a + b ∨ A ∧ B)$ для а = 2, b = 3, A = истина, В = ложь.
Решение. Порядок подсчета значений:
1) b a + a b > a + b, после подстановки получим: 3 2 + 2 3 > 2 + 3, т. е. 17 > 2 + 3 = истина;
2) A ∧ B = истина ∧ ложь = ложь.
Следовательно, выражение в скобках равно (b a + a b > a + b ∨ A ∧ B) = истина ∨ ложь = истина;
3) 1≤ a = 1 ≤ 2 = истина;
Из логических элементов составляются электронные логические схемы, выполняющие более сложные логические операции. Набор логических элементов, состоящий из элементов НЕ, ИЛИ, И, с помощью которых можно построить логическую структуру любой сложности, называется функционально полным.
Построение таблиц истинности логических выражений
Для логической формулы всегда можно записать таблицу истинности, т. е. представить заданную логическую функцию в табличном виде. В этом случае таблица должна содержать все возможные комбинации аргументов функции (формулы) и соответствующие значения функции (результаты формулы на заданном наборе значений).
Удобной формой записи при нахождении значений функции является таблица, содержащая, кроме значений переменных и значений функции, также значения промежуточных вычислений. Рассмотрим пример построения таблицы истинности для формулы $↖ ∧ X2 ∨ ↖ ∨ X1$.
| X1 | X2 | $↖$ | $↖$ \ X2 | X1 ∧ X2 | $↖$ | $↖$ ∧ X2 ∨ $↖$ | $↖$ ∧ X2 ∨ $↖$ ∨ X1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 |
Если функция принимает значение 1 при всех наборах значений переменных, она является тождественно-истинной; если при всех наборах входных значений функция принимает значение 0, она является тождественно-ложной; если набор выходных значений содержит как 0, так и 1, функция называется выполнимой. Приведенный выше пример является примером тождественно-истинной функции.
Зная аналитическую форму логической функции, всегда можно перейти к табличной форме логических функций. С помощью заданной таблицы истинности можно решить обратную задачу, а именно: для заданной таблицы построить аналитическую формулу логической функции. Различают две формы построения аналитической зависимости логической функции по таблично заданной функции.
1. Дизъюнктивно нормальная форма (ДНФ) — сумма произведений, образованных из переменных и их отрицаний для ложных значений.
Алгоритм построения ДНФ следующий:
Пример. Построить функцию, определяющую, что первое число равно второму, используя метод ДНФ. Таблица истинности функции имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 1. Это первая и четвертая строки таблицы (строку заголовка при нумерации не учитываем).
Записываем логические произведения аргументов этих наборов, объединив их логической суммой: X1 ∧ X2 ∨ X1 ∧ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих ложное значение (четвертая строка таблицы; второй набор в формуле; первый и второй элементы): X1 ∧ X2 ∨ $↖$ ∧ $↖$.
2. Конъюнктивно нормальная форма (КНФ) — произведение сумм, образованных из переменных и их отрицаний для истинных значений.
Алгоритм построения КНФ следующий:
Примеры решения задач
Пример 1. Рассмотрим предыдущий пример, т. е. построим функцию, определяющую, что первое число равно второму, используя метод КНФ. Для заданной функции ее таблица истинности имеет вид
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
Решение. Выбираем наборы значений аргументов, в которых функция равна 0. Это вторая и третья строки (строку заголовка при нумерации не учитываем).
Записываем логические суммы аргументов этих наборов, объединив их логическим произведением: X1 ∨ X2 ∧ X1 ∨ X2 .
Записываем отрицание относительно аргументов выбранных наборов, имеющих истинное значение (вторая строка таблицы, первый набор формулы, второй элемент; для третьей строки, а это второй набор формулы, первый элемент): X1 ∨ $↖$ ∧ $↖$ ∨ X2.
Таким образом, получена запись логической функции в КНФ.
Полученные двумя методами значения функций являются эквивалентными. Для доказательства этого утверждения используем правила логики: F(X1, X2) = X1 ∨ $↖$ ∧ $↖$ ∨ X2 = X1 ∧ $↖$ ∨ X1 ∧ X2 ∨ $↖$ ∧ $↖$ ∨ $↖$ ∧ X2 = 0 ∨ X1 ∨ X2 ∨ $↖$ ∧ $↖$ ∨ 0 = X1 ∧ X2 ∨ $↖$ ∧ $↖$.
Пример 2. Построить логическую функцию для заданной таблицы истинности:
| X1 | X2 | F(X1, X2) |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Решение. Используем алгоритм ДНФ для построения исходной функции:
| X1 | X2 | F(X1, X2) | ||
| 1 | 1 | 1 | • | X1 ∧ X2 |
| 1 | 0 | 0 | ||
| 0 | 1 | 1 | • | $↖$ ∧ X2 |
| 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∨ $↖$ ∧ X2 .
Ее можно упростить: X1 ∧ X2 ∨ $↖$ ∧ X2 = X2 ∧ (X1 ∨ $↖$) = X2 ∧ 1 = X2.
Пример 3. Для приведенной таблицы истинности построить логическую функцию, используя метод ДНФ.
| X1 | X2 | X3 | F(X1, X2, X3) | ||
| 1 | 1 | 1 | 1 | • | X1 ∧ X2 ∧ X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 1 | 1 | 1 | • | $↖$ ∧ X2 ∧ X3 |
| 0 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 1 | • | X1 ∧ X2 ∧ $↖$ |
| 1 | 0 | 0 | 1 | • | X1 ∧ $↖$ ∧ $↖$ |
| 0 | 1 | 0 | 0 | ||
| 0 | 0 | 0 | 0 |
Искомая формула: X1 ∧ X2 ∧ X ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∪ X1 ∧ $↖$ ∧ $↖$.
Формула достаточно громоздка, и ее следует упростить:
X1 ∧ X2 ∧ X3 ∨ $↖$ ∧ X2 ∧ X3 ∨ X1 ∧ X2 ∧ $↖$ ∨ X1 ∧ $↖$ ∧ $↖$ = X2 ∧ X3 ∧ (X1 ∨ $↖$) ∨ X1 ∧ $↖$ ∧ (X2 ∨ $↖$) = X2 ∧ X3 ∨ X1 ∧ $↖$.
Таблицы истинности для решения логических задач
Составление таблиц истинности — один из способов решения логических задач. При использовании такого способа решения, условия, которые содержит задача, фиксируются с помощью специально составленных таблиц.
Примеры решения задач
Пример 1. Составить таблицу истинности для охранного устройства, которое использует три датчика и срабатывает при замыкании только двух из них.
| X1 | X2 | X3 | Y(X1, X2, X3) |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 |
Пример 2. Составить расписание уроков на день, учитывая, что урок информатики может быть только первым или вторым, урок математики — первым или третьим, а физики — вторым или третьим. Возможно ли составить расписание, удовлетворив всем требованиям? Сколько существует вариантов расписания?
Решение. Задача легко решается, если составить соответствующую таблицу:
| 1-й урок | 2-й урок | 3-й урок | |
| Информатика | 1 | 1 | 0 |
| Математика | 1 | 0 | 1 |
| Физика | 0 | 1 | 1 |
Из таблицы видно, что существуют два варианта искомого расписания:
- математика, информатика, физика;
- информатика, физика, математика.
Пример 3. В спортивный лагерь приехали трое друзей — Петр, Борис и Алексей. Каждый из них увлекается двумя видами спорта. Известно, что таких видов спорта шесть: футбол, хоккей, лыжи, плавание, теннис, бадминтон. Также известно, что:
- Борис — самый старший;
- играющий в футбол младше играющего в хоккей;
- играющие в футбол и хоккей и Петр живут в одном доме;
- когда между лыжником и теннисистом возникает ссора, Борис мирит их;
- Петр не умеет играть ни в теннис, ни в бадминтон.
Какими видами спорта увлекается каждый из мальчиков?
Решение. Составим таблицу и отразим в ней условия задачи, заполнив соответствующие клетки цифрами 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Так как видов спорта шесть, получается, что все мальчики увлекаются разными видами спорта.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | |||
| Алексей | 0 | 0 |
Из таблицы видно, что в теннис может играть только Алексей.
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 0 | 0 | 0 | ||
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Окончательно получаем, что Борис увлекается хоккеем и бадминтоном. Итоговая таблица будет выглядеть следующим образом:
| Футбол | Хоккей | Лыжи | Плавание | Бадминтон | Теннис | |
| Петр | 0 | 0 | 1 | 1 | 0 | 0 |
| Борис | 0 | 1 | 0 | 0 | 1 | 0 |
| Алексей | 1 | 0 | 0 | 0 | 0 | 1 |
Ответ: Петр увлекается лыжами и плаванием, Борис играет в хоккей и бадминтон, а Алексей занимается футболом и теннисом.
Эта лицензия позволяет другим редактировать, поправлять и брать за основу ваше произведение в некоммерческих целях до тех пор пока они указывают вас в качестве автора и лицензируют их новые творения на идентичных условиях.
Основы логики. Логические операции и таблицы истинности
На данной странице будут рассмотрены 6 логических операций: конъюнкция, дизъюнкция, инверсия, импликация, эквивалентность и исключающие или, которых вам будет достаточно для решения сложных логических выражений. Также мы рассмотрим порядок выполнения данных логических операций в сложных логических выражениях и представим таблицы истинности для каждой логической операции.
Высказывание - это повествовательное предложение, про которое можно определенно сказать истинно оно или ложно (истина (логическая 1), ложь (логический 0)).
Логические операции - мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
Логическое выражение - устное утверждение или запись, в которое, наряду с постоянными величинами, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных величин (объектов) логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).
Сложное логическое выражение - логическое выражение, состоящее из одного или нескольких простых логических выражений (или сложных логических выражений), соединенных с помощью логических операций.
Конъюнкция - это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложенное выражение ложно.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 0 |
2) Логическое сложение или дизъюнкция:
Дизъюнкция - это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия - это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬ A.
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация - это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность - это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
6) Операция XOR (исключающие или)
Обозначение: F = A ⊕ B .
| A | B | F |
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Порядок выполнения логических операций в сложном логическом выражении
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Таблицы истинности можно составить и для произвольной логической функции F(a, b, c…).
В общем случае таблицы истинности имеют размер 2 N строк комбинаций для N независимых логических переменных.
Поскольку таблица истинности выражения состоит из строк со всеми возможными комбинациями значений переменных, она полностью определяет значение выражения.
Законы алгебры логики
Те, кому лень учить эти законы, должны вспомнить алгебру, где знание нескольких способов преобразования позволяет решать очень сложные уравнения.
Строго говоря, это не законы, а теоремы. Но их доказательство не входит в программу изучения. Впрочем, доказательство обычно основывается на построении полной таблицы истинности.
Замечание. Знаки алгебры логики намеренно заменены на сложение и умножение.
Замена операций импликации и эквивалентности
Операций импликации и эквивалентности иногда нет среди логических операций конкретного компьютера или транслятора с языка программирования. Однако для решения многих задач эти операции необходимы. Существуют правила замены данных операций на последовательности операций отрицания, дизъюнкции и конъюнкции.
Так, заменить операцию импликации можно в соответствии со следующим правилом:
A → B = ¬ A \/ B
Для замены операции эквивалентности существует два правила:
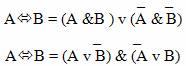
В справедливости данных формул легко убедиться, построив таблицы истинности для правой и левой частей обоих тождеств.
Читайте также:

