Что такое прямой код в информатике кратко

Обновлено: 05.07.2024

Предыдущая лекция | Содержание | Следующая лекция
Информатика. Лекция №5. Представление чисел в компьютере.

Представление целых чисел в компьютере.

Целые числа являются простейшими числовыми данными, с которыми оперирует ЭВМ. Для целых чисел существуют два представления: беззнаковое (только для неотрицательных целых чисел) и со знаком. Очевидно, что отрицательные числа можно представлять только в знаковом виде. Целые числа в компьютере хранятся в формате с фиксированной запятой.

Представление целых чисел в беззнаковых целых типах.

Для беззнакового представления все разряды ячейки отводятся под представление самого числа. Например, в байте (8 бит) можно представить беззнаковые числа от 0 до 255. Поэтому, если известно, что числовая величина является неотрицательной, то выгоднее рассматривать её как беззнаковую.

Представление целых чисел в знаковых целых типах.

Для представления со знаком самый старший (левый) бит отводится под знак числа, остальные разряды - под само число. Если число положительное, то в знаковый разряд помещается 0, если отрицательное - 1. Например, в байте можно представить знаковые числа от -128 до 127.

Прямой код числа.

Дополнительный код числа.

Дополнительный код положительного числа равен прямому коду этого числа. Дополнительный код отрицательного числа m равен 2 k -|m|, где k - количество разрядов в ячейке.
Как уже было сказано, при представлении неотрицательных чисел в беззнаковом формате все разряды ячейки отводятся под само число. Например, запись числа 243=11110011 в одном байте при беззнаковом представлении будет выглядеть следующим образом:

При представлении целых чисел со знаком старший (левый) разряд отводится под знак числа, и под собственно число остаётся на один разряд меньше. Поэтому, если приведённое выше состояние ячейки рассматривать как запись целого числа со знаком, то для компьютера в этой ячейке записано число -13 (243+13=256=28).
Но если это же отрицательное число записать в ячейку из 16-ти разрядов, то содержимое ячейки будет следующим:

Знаковый разряд
Возникает вопрос: с какой целью отрицательные числа записываются в виде дополнительного кода и как получить дополнительный код отрицательного числа?
Дополнительный код используется для упрощения выполнения арифметических операций. Если бы вычислительная машина работала с прямыми кодами положительных и отрицательных чисел, то при выполнении арифметических операций следовало бы выполнять ряд дополнительных действий. Например, при сложении нужно было бы проверять знаки обоих операндов и определять знак результата. Если знаки одинаковые, то вычисляется сумма операндов и ей присваивается тот же знак. Если знаки разные, то из большего по абсолютной величине числа вычитается меньшее и результату присваивается знак большего числа. То есть при таком представлении чисел (в виде только прямого кода) операция сложения реализуется через достаточно сложный алгоритм. Если же отрицательные числа представлять в виде дополнительного кода, то операция сложения, в том числе и разного знака, сводится к из поразрядному сложению.

Для компьютерного представления целых чисел обычно используется один, два или четыре байта, то есть ячейка памяти будет состоять из восьми, шестнадцати или тридцати двух разрядов соответственно.

Алгоритм получения дополнительного кода отрицательного числа.

модуль отрицательного числа представить прямым кодом в k двоичных разрядах;
значение всех бит инвертировать:все нули заменить на единицы, а единицы на нули(таким образом, получается k-разрядный обратный код исходного числа);
к полученному обратному коду прибавить единицу.

Можно заметить, что представление целого числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление:

Представление вещественных чисел в компьютере.

Для представления вещественных чисел в современных компьютерах принят способ представления с плавающей запятой. Этот способ представления опирается на нормализованную (экспоненциальную) запись действительных чисел.
Как и для целых чисел, при представлении действительных чисел в компьютере чаще всего используется двоичная система, следовательно, предварительно десятичное число должно быть переведено двоичную систему.

Нормализованная запись числа.

Нормализованная запись отличного от нуля действительного числа - это запись вида a= m*P q , где q - целое число (положительное, отрицательное или ноль), а m - правильная P-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть . При этом m называется мантиссой числа, q - порядком числа.

3,1415926 = 0, 31415926 * 10 1 ;
1000=0,1 * 10 4 ;
0,123456789 = 0,123456789 * 10 0 ;
0,0000107₈ = 0,1078 * 8 -4 ; (порядок записан в 10-й системе)
1000,0001₂ = 0, 100000012 * 2 4 .

Нормализованная экспоненциальная запись числа - это запись вида a= m*P q , где q - целое число (положительное, отрицательное или ноль), а m - P-ичная дробь, у которой целая часть состоит из одной цифры. При этом (m-целая часть) называется мантиссой числа, q - порядком числа.

Представление чисел с плавающей запятой.

При представлении чисел с плавающей запятой часть разрядов ячейки отводится для записи порядка числа, остальные разряды - для записи мантиссы. По одному разряду в каждой группе отводится для изображения знака порядка и знака мантиссы. Для того, чтобы не хранить знак порядка, был придуман так называемый смещённый порядок, который рассчитывается по формуле 2 a-1 +ИП, где a - количество разрядов, отводимых под порядок.

Пример:
Если истинный порядок равен -5, тогда смещённый порядок для 4-байтового числа будет равен 127-5=122.

Алгоритм представления числа с плавающей запятой.

Перевести число из p-ичной системы счисления в двоичную;
представить двоичное число в нормализованной экспоненциальной форме;
рассчитать смещённый порядок числа;
разместить знак, порядок и мантиссу в соответствующие разряды сетки.

Можно заметить, что представление действительного числа не очень удобно изображать в двоичной системе, поэтому часто используют шестнадцатеричное представление:

Выбор способа хранения целых чисел в памяти компьютера — не такая тривиальная задача, как могло бы показаться на первый взгляд. Желательно, чтобы этот способ:

не требовал усложнения архитектуры процессора для выполнения арифметических операций с отрицательными числами,
не усложнял арифметические действия,
хранил бы одинаковое количество положительных и отрицательных чисел.

Рассмотрим разные методы представления.

Содержание

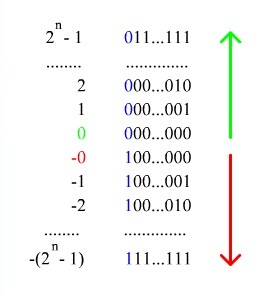
При записи числа в прямом коде (англ. Signed magnitude representation) старший разряд является знаковым разрядом. Если его значение равно нулю, то представлено положительное число или положительный ноль, если единице, то представлено отрицательное число или отрицательный ноль. В остальных разрядах (которые называются цифровыми) записывается двоичное представление модуля числа. Например, число [math] -5 [/math] в восьмибитном типе данных, использующем прямой код, будет выглядеть так: [math] 10000101 [/math] .

Таким способом в [math] n [/math] -битовом типе данных можно представить диапазон чисел [math] [-2^ + 1; 2^ - 1] [/math] .

Получить прямой код числа достаточно просто.
Из-за того, что [math]0[/math] обозначает [math]+[/math] , коды положительных чисел относительно беззнакового кодирования остаются неизменными.
Количество положительных чисел равно количеству отрицательных.

Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора (например, для вычитания невозможно использовать сумматор, необходима отдельная схема для этого).
Существуют два нуля: [math] -0 [/math] [math](100 \ldots 000) [/math] и [math] +0 [/math] [math] (000 \ldots 000) [/math] , из-за чего усложняется арифметическое сравнение.

Из-за весьма существенных недостатков прямой код используется очень редко.

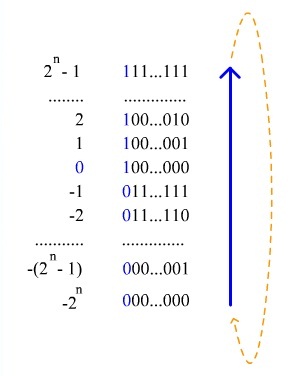
Код со сдвигом. Как видно, двоичное представление зациклено по модулю [math]1000..000_[/math] ( [math]n[/math] нулей)

При использовании кода со сдвигом (англ. Offset binary) целочисленный отрезок от нуля до [math] 2^n [/math] ( [math] n [/math] — количество бит) сдвигается влево на [math] 2^ [/math] , а затем получившиеся на этом отрезке числа последовательно кодируются в порядке возрастания кодами от [math] 000 \dots 0 [/math] до [math] 111 \dots 1 [/math] . Например, число [math] -5 [/math] в восьмибитном типе данных, использующем код со сдвигом, превратится в [math] -5 + 128 = 123 [/math] , то есть будет выглядеть так: [math] 01111011 [/math] .

По сути, при таком кодировании:

к кодируемому числу прибавляют [math] 2^ [/math] ;
переводят получившееся число в двоичную систему исчисления.

Можно получить диапазон значений [math] [-2^; 2^ - 1][/math] .

Не требуется усложнение архитектуры процессора.
Нет проблемы двух нулей.

Из-за необходимости усложнять арифметические операции код со сдвигом для представления целых чисел используется не часто, но зато применяется для хранения порядка вещественного числа.

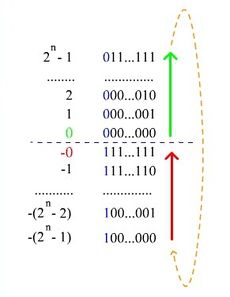
Нумерация двоичных чисел в представлении c дополнением до единицы. В отличии от кода со сдвигом, нулю соответствуют коды [math] 00. 000 [/math] и [math] 11. 111 [/math]

В качестве альтернативы представления целых чисел может использоваться код с дополнением до единицы (англ. Ones' complement).

Алгоритм получения кода числа:

если число положительное, то в старший разряд (который является знаковым) записывается ноль, а далее записывается само число;
если число отрицательное, то код получается инвертированием представления модуля числа (получается обратный код);
если число является нулем, то его можно представить двумя способами: [math] +0 [/math] [math](000 \ldots 000) [/math] или [math] -0 [/math] [math] (111 \ldots 111) [/math] .

Пример: переведём число [math] -13 [/math] в двоичный восьмибитный код. Прямой код модуля [math] -13 [/math] : [math] 00001101 [/math] , инвертируем и получаем [math] 11110010 [/math] . Для получения из дополнительного кода самого числа достаточно инвертировать все разряды кода.

Таким способом можно получить диапазон значений [math] [-2^+1; 2^ - 1] [/math] .

Простое получение кода отрицательных чисел.
Из-за того, что [math]0[/math] обозначает [math]+[/math] , коды положительных чисел относительно беззнакового кодирования остаются неизменными.
Количество положительных чисел равно количеству отрицательных.

Выполнение арифметических операций с отрицательными числами требует усложнения архитектуры центрального процессора.
Существуют два нуля: [math] +0 [/math] и [math] -0 [/math] .

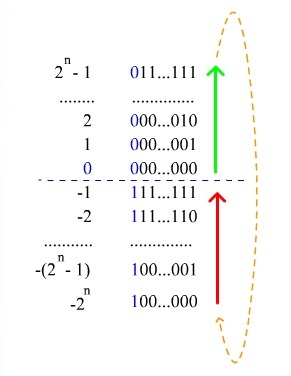
Чаще всего для представления отрицательных чисел используется код с дополнением до двух (англ. Two's complement).

Алгоритм получения дополнительного кода числа:

если число неотрицательное, то в старший разряд записывается ноль, далее записывается само число;
если число отрицательное, то все биты модуля числа инвертируются, то есть все единицы меняются на нули, а нули — на единицы, к инвертированному числу прибавляется единица, далее к результату дописывается знаковый разряд, равный единице.

В качестве примера переведём число [math] -5 [/math] в дополнительный восьмибитный код. Прямой код модуля [math] -5 [/math] : [math] 0000101 [/math] , обратный — [math] 1111010 [/math] , прибавляем [math] 1 [/math] , получаем [math] 1111011 [/math] , приписываем [math] 1 [/math] в качестве знакового разряда, в результате получаем [math] 11111011 [/math] .

Также дополнительный код отрицательного числа [math] A [/math] , хранящегося в [math] n [/math] битах, равен [math] 2^n - |A| [/math] . По сути, дополнительный код представляет собой дополнение [math] |A| [/math] до [math] 0 [/math] : так как в [math] n [/math] -разрядной арифметике [math] 2^ = 0 [/math] (двоичная запись этого числа состоит из единицы и [math] n [/math] нулей, а в [math] n [/math] -разрядную ячейку помещаются только [math] n [/math] младших разрядов, то есть [math] n [/math] нулей), то верно равенство [math] 2^n - |A| + |A| = 0 [/math] .

Для получения из дополнительного кода самого числа нужно инвертировать все разряды кода и прибавить к нему единицу. Можно проверить правильность, сложив дополнительный код с самим числом: результат должен быть равен [math] 2^n [/math] . Переведём [math] 11111011 [/math] обратно. Инвертируем — [math] 00000100 [/math] , прибавляем [math] 1 [/math] , получаем [math] 00000101 [/math] — модуль исходного числа [math] -5 [/math] . Проверим: [math] 11111011 + 00000101 = 100000000 [/math] .

Можно получить диапазон значений [math] [-2^; 2^ - 1] [/math] .

Дополнительный код также удобно использовать для вычислений в длинной арифметике, особенно для операций сложения и вычитания. Это операции удобно выполнять с числами одинаковой длины, поэтому в старшие разряды меньшего числа нужно поместить нули (если число положительно) или единицы (если число отрицательно). Тогда числа будут выглядеть следующим образом: в старших разрядах бесконечное число нулей (единиц), а в младших разрядах уже встречаются и нули, и единицы, которые кодируют само число, а не знак. Удобство заключается в том, что нам не обязательно проделывать операции сложения с каждой парой бит, если мы знаем, что на этом отрезке в числах стоят либо единицы, либо нули. Таким образом, на этом отрезке в получившемся числе тоже будут либо только единицы, либо только нули. Операцию сложения можно выполнить только один раз для старших битов, таким образом мы узнаем знак получившегося числа. Вычитание тоже выполняется просто: инвертируем число, прибавляем один и получаем это число с минусом, затем просто делаем сложение. Однако умножение с числами, представленными дополнительным кодом, выполнять не всегда оптимально: алгоритм либо слишком медленный (наивный алгоритм работает за [math]O(n^2)[/math] ), либо слишком сложный. Лучше для умножение использовать прямой код (бит под знак). Тогда можно числа перевести в десятичную систему счисления, выполнить быстрое преобразование Фурье за [math]O(n \log n)[/math] , затем перевести их обратно в двоичную. Обычно такой алгоритм работает быстрее, чем выполнение операции напрямую с двоичными числами. Для деления обычно тоже лучше использовать прямой код.

Возможность заменить арифметическую операцию вычитания операцией сложения и сделать операции сложения одинаковыми для знаковых и беззнаковых типов данных, что существенно упрощает архитектуру процессора и увеличивает его быстродействие.
Нет проблемы двух нулей.

Ряд положительных и отрицательных чисел несимметричен, но это не так важно: с помощью дополнительного кода выполнены гораздо более важные вещи, желаемые от способа представления целых чисел.
В отличие от сложения, числа в дополнительном коде нельзя сравнивать как беззнаковые, или вычитать без расширения разрядности.

Несмотря на недостатки, дополнение до двух в современных вычислительных системах используется чаще всего.

Прямой, обратный и дополнительный коды — это методы отображения двоичных чисел, имеющих фиксированную запятую, в компьютерных вычислительных операциях, которые предназначены для представления отрицательных и положительных чисел.

Введение

Прямой, обратный и дополнительный коды двоичных чисел являются способами отображения двоичных чисел, имеющих фиксированную запятую, в компьютерных вычислительных операциях, которые предназначены для представления отрицательных и положительных чисел. Известно, что любые десятичные числа можно представить в двоичном коде. Например, десятичное число 101 в двоичном формате равняется 1100101, или в восьми битном формате это выглядит как 0110 0101. А чтобы представить отрицательные десятичные числа в двоичном виде и обеспечить возможность выполнения с ними арифметических операций, как раз и предназначены различные методы отображения чисел в двоичном коде.

Прямой, обратный и дополнительный коды

Следует подчеркнуть, что положительные числа в двоичном коде не зависимо от метода их представления, то есть в прямом, обратном или дополнительном кодах, обладают одинаковым видом.

Прямой код является методом отображения двоичных чисел с фиксированной запятой, который в основном применяется для записи неотрицательных чисел. Прямой код может применяться в следующих вариантах:

В основном варианте он служит для записи только неотрицательных чисел. В этом случае для восьми битного двоичного числа может быть записано максимальное число 255 (всего чисел 256, то есть, от нуля до 255).
Во втором варианте он служит для записи как положительных, так и отрицательных чисел.

Во втором случае старший бит принято считать знаковым разрядом (знаковым битом). Причём, если:

Знаковый разряд равняется нулю, то число является положительным.
Знаковый разряд равняется единице, то число является отрицательным.

В таком варианте диапазон десятичных чисел, которые могут быть записаны в прямом коде, составляет от - 127 до +127.

Готовые работы на аналогичную тему

Таким образом, на основании изложенного выше можно сделать вывод, что прямой код может применяться в основном для представления неотрицательных чисел. Применение прямого кода для представления отрицательных чисел считается малоэффективным, поскольку при этом достаточно сложно реализовать арифметические операции и, помимо этого, в прямом коде существует два представления нуля, а именно, положительный нуль и отрицательный нуль (чего не бывает).

Обратный код является способом вычислительной математики, который позволяет осуществить вычитание одного числа из другого, применяя лишь операцию суммирования. Обратный двоичный код положительного числа представляет собой одноразрядный код знака, то есть, двоичного числа нуль, за которым должно следовать числовое значение.

Обратные двоичные коды отрицательных чисел представляет собой одноразрядный код знака, а именно, двоичную цифру единица, за которой должны следовать инвертированные значения положительных чисел. Для положительных чисел обратный код двоичных чисел обладает таким же видом, что и представление неотрицательных чисел в прямом коде.

Для отрицательных чисел обратный код может быть получен из неотрицательного числа в прямом коде, путем инвертирования всех битов, то есть, единицы заменяются нулями, а нули должны быть заменены на единицы. Для преобразования отрицательного числа, которое записано в обратном коде, в положительное необходимо просто выполнить его инвертирование. Для восьми битного двоичного числа знаковым битом, как и в прямом коде, является старший, то есть, восьмой бит. Диапазон десятичных чисел, которые могут быть записаны в обратном коде, простирается от -127 до + 127. Ниже приведены примеры записи чисел в обратном коде.

Рисунок 1. Примеры записи чисел в обратном коде. Автор24 — интернет-биржа студенческих работ

Далее рассмотрим выполнение арифметических операций с отрицательными числами в обратном коде (арифметические операции с двоичными числами).

Имеем следующие два числа:

Необходимо выполнить их сложение, которое в десятичном формате имеет общеизвестный вид:

100 + (–25) = 100 - 25 = 75

Для реализации этой операции в двоичных кодах, необходимо сначала выполнить перевод числа -25 в двоичное число в обратном коде:

Затем необходимо осуществить собственно операцию сложения двух чисел:

0110 0100 (100) + 1110 0110 (–25) = 1 0100 1010.

Старший единичный разряд необходимо отбросить, так как получился лишний девятый разряд, как результат переполнения:

Далее отброшенную в результате старшую единицу следует прибавить к результату:

0100 1010 + 1 = 0100 1011.

При этом знаковый бит равняется нулю и это означает, что число является положительным и равным 75 в десятичной системе.

Обратный код способен решить проблему сложения и вычитания чисел с разными знаками, но также и обладает определёнными недостатками:

Для выполнения арифметических операций необходимо осуществить два этапа.
Как и для прямого кода существует два представления нуля, а именно, положительный и отрицательный.

Дополнительный код является самым распространенным способом представления отрицательных чисел. Он предоставляет возможность замены операции вычитания операцией сложения, а также позволяет сделать операции сложения и вычитания одинаковыми для знаковых и без знаковых чисел.

Дополнительный код, аналогично прямому и обратному кодам, использует старший разряд для обозначения знака числа, то есть, этот разряд является знаковым битом. Диапазон десятичных чисел, которые могут быть записаны в дополнительном коде, простирается от -128 до +127. Запись положительных двоичных чисел в дополнительном коде выполняется так же, как и в прямом и обратном кодах.

Дополнительный код отрицательного числа может быть получен следующими способами:

где I - количество информации;
N - количество возможных событий;
р_i - вероятность i-го события.

Бит — слишком мелкая еденица измерения. На практике чаще применяются более крупная еденица — байт равная восьми битам. Именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2 8 ).

Широко используются также ещё более крупные производные еденицы информации:

1 Килобайт (Кбайт) = 1024 байта = 2 10 байт
1 Мегабайт (Мбайт) = 1024 Кбайт = 2 20 байт
1 Гигабайт (Гбайт) = 1024 Мбайт = 2 30 байт

В последнее время в связи с увелечением объёмов информации входят в употребление такие производные еденицы как:

1 Терабайт (Тбайт) = 1024 Гбайт = 2 40 байт
1 Петабайт (Пбайт) = 1024 Тбайт = 2 50 байт

Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством , где B — непустое множество, над элементами которого определены три операции:

· отрицание (унарная операция),

· конъюнкция (бинарная),

· дизъюнкция (бинарная),

· а также константы — логический ноль 0 и логическая единица 1.

· Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например ). Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например ).

· Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов:

· Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.

· Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция приобретает смысл вычитания из единицы; — немодульного сложения; & — умножения; — равенства; — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR); — непревосходства суммы над 1 (то есть A B = (A + B)

· Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.

· Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.

Двоичная система счисления используется для кодирования дискретного сигнала, потребителем которого является вычислительная техника. Такое положение дел сложилось исторически, поскольку двоичный сигнал проще представлять на аппаратном уровне. В этой системе счисления для представления числа применяются два знака – 0 и 1.

Шестнадцатеричная система счисления используется для кодирования дискретного сигнала, потребителем которого является хорошо подготовленный пользователь – специалист в области информатики. В такой форме представляется содержимое любого файла, затребованное через интегрированные оболочки операционной системы, например, средствами Norton Commander в случае MS DOS. Используемые знаки для представления числа – десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F.

Десятичная система счисления используется для кодирования дискретного сигнала, потребителем которого является так называемый конечный пользователь – неспециалист в области информатики (очевидно, что и любой человек может выступать в роли такого потребителя). Используемые знаки для представления числа – цифры от 0 до 9.

Непозиционная система счисления – система, в которой символы, обозначающие то или иное количество, не меняют своего значения в зависимости от местоположения (позиции) в изображении числа.

Непозиционной системой счисления является самая простая система с одним символом (палочкой). Для изображения какого-либо числа в этой системе надо записать количество палочек, равное данному числу. Например, запись числа 12 в такой системе счисления будет иметь вид: IIIIIIIIIIII. Эта система неэффективна, так как форма записи очень громоздка.

К непозиционной системе счисления относится и римская, символы алфавита которой и обозначаемое ими количество представлены в таблице.

Римские цифры	I	V	X	L	С	D	М
Значение (обозначаемое количество)

Представление чисел в ЭВМ. Примеры записи. Положительные и отрицательные числа в двоичной системе. Прямой и обратный код. Мантисса и порядок. Запись основания десятичной системы счисления в ЭВМ.

Машинным изображением числа называют его представление в разрядной сетке ЭВМ. В вычислительных машинах применяются две формы представления чисел:

естественная форма или форма с фиксированной запятой (точкой);
нормальная форма или форма с плавающей запятой (точкой);

(естественная форма) 452,34 = 452340*10 -3 = 0,0045234*10 5 = 0,45234*10 3 (нормальная форма)

Всякое десятичное число, прежде чем оно попадает в память компьютера, преобразуется по схеме:

После этого осуществляется ещё одна важная процедура:

мантисса с её знаком заменяется кодом мантиссы с её знаком;
порядок числа с его знаком заменяется кодом порядка с его знаком.

Указанные коды двоичных чисел - это образы чисел, которые и воспринимают вычислительные устройства. Каждому двоичному числу можно поставить в соответствие несколько видов кодов.

Существуют следующие коды двоичных чисел:

Прямой код;
Обратный код;
Дополнительный код.

Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией сложения.

Прямой код

Положительные числа в ЭВМ всегда представляются с помощью прямого кода. Прямой код числа полностью совпадает с записью самого числа в ячейке машины. Вообще, положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде.

Например,

Прямой код отрицательного числа отличается от прямого кода соответствующего положительного числа лишь содержимым знакового разряда. Но отрицательные целые числа не представляются в ЭВМ с помощью прямого кода, для их представления используется так называемый дополнительный код.

Прямой код двоичного числа(а это либо мантисса, либо порядок) образуется по такому алгоритму:

1.Определить данное двоичное число - оно либо целое (порядок), либо правильная дробь (мантисса).

2.Если это дробь, то цифры после запятой можно рассматривать как целое число.

3.Если это целое и положительное двоичное число, то вместе с добавлением 0 в старший разряд число превращается в код. Для отрицательного двоичного числа перед ним ставится единица.

Например,

Информация: связь с неопределенностью, формула Шеннона, единицы измерения, элементы алгебры Буля, системы счисления (непозиционные системы, перевод из одной системы в другую, обратный перевод)

(2.2)

где I - количество информации;
N - количество возможных событий;
р_i - вероятность i-го события.

Широко используются также ещё более крупные производные еденицы информации:

1 Килобайт (Кбайт) = 1024 байта = 2 10 байт
1 Мегабайт (Мбайт) = 1024 Кбайт = 2 20 байт
1 Гигабайт (Гбайт) = 1024 Мбайт = 2 30 байт

1 Терабайт (Тбайт) = 1024 Гбайт = 2 40 байт
1 Петабайт (Пбайт) = 1024 Тбайт = 2 50 байт

· отрицание (унарная операция),

· конъюнкция (бинарная),

· дизъюнкция (бинарная),

· а также константы — логический ноль 0 и логическая единица 1.

Всякое десятичное число, прежде чем оно попадает в память компьютера, преобразуется по схеме:

После этого осуществляется ещё одна важная процедура:

мантисса с её знаком заменяется кодом мантиссы с её знаком;
порядок числа с его знаком заменяется кодом порядка с его знаком.

Существуют следующие коды двоичных чисел:

Прямой код;
Обратный код;
Дополнительный код.

Прямой код

Например,

Прямой код двоичного числа(а это либо мантисса, либо порядок) образуется по такому алгоритму:

1.Определить данное двоичное число - оно либо целое (порядок), либо правильная дробь (мантисса).

2.Если это дробь, то цифры после запятой можно рассматривать как целое число.

Например,

Читайте также: