Что такое неравенство треугольника кратко
Обновлено: 03.07.2024
свойство геометрии, также используется для обобщения понятия "расстояние" в метрических пространствах.
Три примера неравенства треугольника для треугольников со сторонами длин Икс , у , z . В верхнем примере показан случай, когда z намного меньше суммы Икс + у двух других сторон, а в нижнем примере показан случай, когда сторона z лишь немного меньше, чем Икс + у .
В математика, то неравенство треугольника заявляет, что для любого треугольник, сумма длин любых двух сторон должна быть больше или равна длине оставшейся стороны. [1] [2] Это утверждение допускает включение вырожденные треугольники, но некоторые авторы, особенно те, кто пишет об элементарной геометрии, исключают эту возможность, тем самым упуская возможность равенства. [3] Если Икс , у , и z - длины сторон треугольника, причем ни одна из сторон не превышает z , то неравенство треугольника утверждает, что
с равенством только в вырожденном случае треугольника нулевой площади. Евклидова геометрия и некоторых других геометрий неравенство треугольника является теоремой о расстояниях, и оно записывается с использованием векторов и векторных длин (нормы):
где длина z третьей стороны заменена векторной суммой Икс + у . Когда Икс и у находятся действительные числа, их можно рассматривать как векторы в ℝ 1 , а неравенство треугольника выражает связь между абсолютные значения.
В евклидовой геометрии для прямоугольные треугольники неравенство треугольника является следствием теорема Пифагора, а для общих треугольников следствие закон косинусов, хотя это может быть доказано и без этих теорем. Неравенство интуитивно можно увидеть либо в ℝ 2 или ℝ 3 . На рисунке справа показаны три примера, начиная с явного неравенства (вверху) и приближаясь к равенству (внизу). В евклидовом случае равенство имеет место только в том случае, если треугольник имеет 180° угол и два 0° углы, делая три вершины коллинеарен, как показано в нижнем примере. Таким образом, в евклидовой геометрии кратчайшее расстояние между двумя точками - прямая линия.
В сферическая геометрия, кратчайшее расстояние между двумя точками - дуга большой круг, но неравенство треугольника выполняется при условии, что расстояние между двумя точками на сфере равно длине малого сферического отрезка прямой (то есть отрезка с центральным углом в [0, π ] ) с этими конечными точками. [4] [5]
Неравенство треугольника есть определение собственности из нормы и меры расстояние. Это свойство должно быть установлено как теорема для любой функции, предлагаемой для таких целей для каждого конкретного пространства: например, таких пространств, как действительные числа, Евклидовы пространства, то L п пробелы ( п ≥ 1 ), и внутренние пространства продукта.
Понятие термина неравенство треугольника и его сторон
Определение: неравенство треугольника в геометрии, математическом анализе и смежных дисциплинах — это свойство, при котором длина любой стороны треугольника всегда меньше суммы длин двух других его сторон.
Теорема о неравенстве треугольников вытекает из теоремы о соотношении сторон и углов треугольника: против большей стороны в треугольнике лежит больший угол и, наоборот, против большего угла лежит большая сторона.
А В > А С > В С , ∠ С > ∠ В > ∠ А .
Теорема о неравенстве треугольника
Основная формулировка: каждая сторона треугольника меньше суммы двух других сторон.
Доказать: А В А С + С В .
Проведем C D = C B , A C + C D = A D . ∠ 1 = ∠ 2 .
В треугольнике АВD требуется доказать, что АВ
Пользуясь теоремой о соотношении углов и сторон: А В A D = A C + C B .
Что и требовалось доказать.
Формула и следствие
Для любых трех точек А, В, С, не лежащих на одной прямой справедливы неравенства:
Длина каждой стороны треугольника больше разности длин двух других его сторон.
По теореме о неравенстве треугольника:
Примеры решения задач
Существует ли треугольник со сторонами: 1 м , 2 м , 3 м .
Решение: по теореме о неравенстве треугольника 3 = 2 + 1 ⇒ 3 = 3
Ответ: такого треугольника не существует.
Существует ли треугольник со сторонами: 3 м , 4 м , 5 м .
Ответ: такой треугольник существует.
Краткие упражнения для самостоятельной работы
Одна сторона треугольника равна 2, другая 5. Какой может быть третья сторона, если известно, что ее длина тоже целое число?
Периметр равнобедренного треугольника равен 13, при этом две его стороны отличаются по длине на 4. Чему могут быть равны эти стороны?
Одна сторона треугольника равна 12, другая 5. Чему может быть равна самая короткая сторона этого треугольника? Самая длинная? Средняя по длине?

Любая фигура имеет некие рамки, пропорции длин сторон. В реальной жизни они помогают определить, можно ли изготовить треугольное основание определенных пропорций, насколько возможно создать линзу той или иной формы или может ли удержаться табуретка на треугольном, квадратном или любом другом основании. В теоретической геометрии пропорции, как правило, применяют для решения задач на доказательство или для определения правильности условия задачи.
Теорема о неравенстве треугольника
Именно с этой теоремы должно начинаться любое решение задачи. Но, как правило, это действие опускают. Считается, что составитель задач не может предложить условие с несуществующим треугольником.
Теорема о неравенстве сторон треугольника гласит, что каждая сторона треугольника всегда меньше или равна сумме двух других его сторон.
По факту, любая сторона треугольника всегда меньше суммы двух других его сторон. Равенство возможно, только если все три вершины треугольника лежат на одной линии. Можно ли считать такую фигуру треугольником – вопрос философов, а не математиков. Поэтому в формулировке ставится знак больше или равно.

Рис. 1. Виды треугольников
Доказать это определение можно двумя способами: через аксиому Евклида или через высоту треугольника. Последний способ более логичен, тогда как второй – короче. Какой выбрать – решает доказывающий.
Доказательство через аксиому

Существует аксиома, которая говорит, что для трех точек А, В, С не лежащих на одной прямой справедливо утверждение: АВ Рис. 2. Рисунок к доказательству
В произвольном треугольнике АВС проведем высоту АН. Высота разобьет произвольный треугольник на два прямоугольных. Тогда для каждого из прямоугольных треугольников в виде неравенств запишем, что катет всегда меньше гипотенузы.
Гипотенуза всегда больше катета потому, что в треугольнике действует отношение сторон и углов. Поэтому напротив наибольшего угла всегда находится наибольшая сторона. А в треугольнике наибольшим углом всегда является угол в 90 градусов.

ВН Рис. 3. Рисунок к доказательству
Теорема 1 Любая сторона треугольника меньше суммы двух других сторон.
Доказательство. Рассмотрим произвольный треугольник ABC (Рис.1).
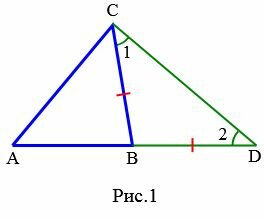 |
Докажем, что \( \small AC \lt AB+BC .\) На продолжении стороны AB отложим отрезок BD равный стороне BC. Полученный треугольник BCD равнобедренный. тогда \( \small \angle 1= \angle 2.\) Рассмотрим треугольник ADC. В этом треугольнике \( \small \angle ACD \gt \angle 1 \) и учитывая, что \( \small \angle 1= \angle 2, \) получим \( \small \angle ACD \gt \angle 2. \) По теореме 1 статьи Соотношения между сторонами и углами треугольника, против большего угла треугольника лежит большая сторона. Следовательно в треугольнике ADC имеет место неравенство:
Тогда из (1) и (2) получим:
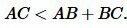  |
Следствие 1. Для любых точек A, B, C, не расположенных на одной прямой справедливы следующие неравенства:
Читайте также:

