Что такое медиана треугольника кратко

Обновлено: 05.07.2024

Определение . Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны (рис 1).

Поскольку в каждом треугольнике имеется три вершины, то в каждом треугольнике можно провести три медианы.

На рисунке 1 медианой является отрезок BD .

Утверждение 1 . Медиана треугольника делит его на два треугольника равной площади ( равновеликих треугольника).

Доказательство . Проведем из вершины B треугольника ABC медиану BD и высоту BE (рис. 2),

Поскольку отрезок BD является медианой, то

что и требовалось доказать.

Утверждение 2 . Точка пересечения двух любых медиан треугольника делит каждую из этих медиан в отношении 2 : 1 , считая от вершины треугольника.

Доказательство . Рассмотрим две любых медианы треугольника, например, медианы AD и CE , и обозначим точку их пересечения буквой O (рис. 3).

Обозначим середины отрезков AO и CO буквами F и G соответственно (рис. 4).

Теперь рассмотрим четырёхугольник FEDG (рис. 5).

Сторона ED этого четырёхугольника является средней линией в треугольнике ABC . Следовательно,

Сторона FG четырёхугольника FEDG является средней линией в треугольнике AOC . Следовательно,

Отсюда вытекает, что точка O делит каждую из медиан AD и CE в отношении 2 : 1 , считая от вершины треугольника.

Следствие . Все три медианы треугольника пересекаются в одной точке.

Доказательство . Рассмотрим медиану AD треугольника ABC и точку O , которая делит эту медиану в отношении 2 : 1 , считая от вершины A (рис.7).

Поскольку точка, делящая отрезок в заданном отношении, является единственной, то и другие медианы треугольника будут проходить через эту точку, что и требовалось доказать.

Определение . Точку пересечения медиан треугольника называют центроидом треугольника.

Утверждение 3 . Медианы треугольника делят треугольник на 6 равновеликих треугольников (рис. 8).

Доказательство . Докажем, что площадь каждого из шести треугольников, на которые медианы разбивают треугольник ABC , равна площади треугольника ABC. Для этого рассмотрим, например, треугольник AOF и опустим из вершины A перпендикуляр AK на прямую BF (рис. 9).

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
AB – самая короткая сторона, следовательно, медиана CD – самая длинная.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Медиана — это золотое сечение треугольника

У этого слова несколько значений, и обо всех мы упомянем. Но в первую очередь нас интересует то, с которым знакомят школьников на уроках геометрии ближе к старшим классам.

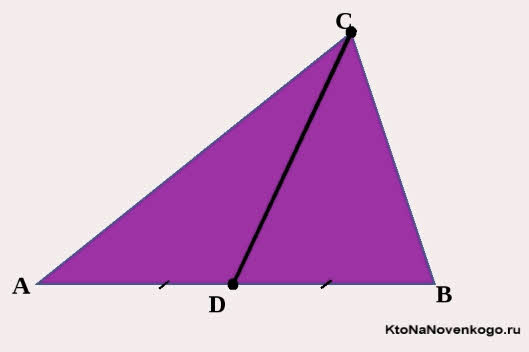
И в этом случае МЕДИАНА имеет непосредственное отношение к такой геометрической фигуре, как треугольник.

Медиана — это.

Медиана – это отрезок или часть прямой линии, которая проведена из вершины треугольника к середине противоположной стороны. Точно так же называется и длина этого отрезка.

Вот обратите внимание на этот простой, но очень наглядный рисунок. На нем изображен треугольник со сторонами АВ, АС и ВС, или как принято писать в математике — треугольник АВС.

Точка М – это середина стороны ВС. И соответственно линия АМ, проведенная из вершины А до середины стороны ВС, и есть МЕДИАНА.

Еще раз повторим! Медиана – понятие, которое имеет отношение только к треугольникам. У других похожие линии называются по-другому. Например, у прямоугольников и квадратов – это диагональ. А у окружности – это диаметр.

Есть в треугольнике обычном
Отрезок очень непростой
Соединяет он обычно с серединой стороны любой
И каждый должен знать отлично,
Зовется медианой он.

И из этого можно сделать логический вывод, что медиан у любого треугольника может быть несколько. А точнее, три!

И выглядят они вот так.

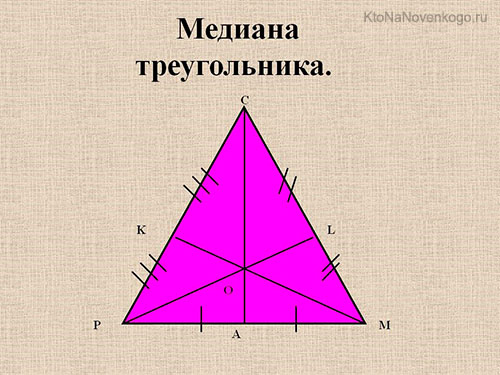
На этом рисунке мы отчетливо видим все три медианы. Они обозначаются отрезками CA, PL и KM.

Пересечение медиан треугольника

Точка О, в которой пересекаются все медианы треугольника, также имеет свое особое название. И даже несколько – центр тяжести, центроид, геометрический центр, барицентр, центр инерции. Ну а неформально эту точку называют точкой равновесия.

Чтобы лучше понять, что это такое, представьте себе треугольник, вырезанный из бумаги или картона. Если вы на нем проведете все три медианы и найдете точку их пересечения, то подставив под нее палец, вы сможете удерживать ваш картонный треугольник в равновесии, не давая ему упасть.

Важно! С точкой пересечения медиан связан один математический факт. Она делит каждую медиану на два отрезка, соотношение которых составляет 2 к 1, если считать от вершины.

Если для примера взять указанный выше треугольник, то тогда это правило можно расписать следующим образом:

Отрезок СО вдвое больше, чем отрезок АО;
Отрезок РО вдвое больше, чем отрезок LO;
Отрезок МО вдвое больше, чем КО.

Это правило не требует доказательств. Но если хотите, можете провести в домашних условиях опыт и убедиться в правдивости расчетов.

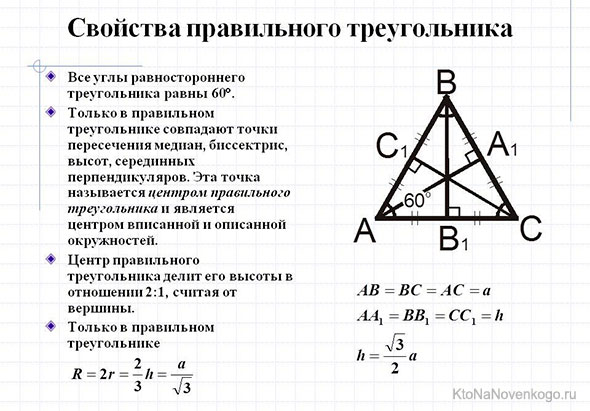
Медиана равностороннего треугольника

Равносторонний треугольник сам по себе уникален, так как все его три стороны имеют одинаковую длину. Логично предположить, что и медиана в нем какая-то особенная?! Да, так оно и есть.

Медиана в равностороннем треугольнике является одновременно и высотой, и биссектрисой.

Если кто не знает, высотой в треугольнике называют отрезок, который опускается из вершины перпендикулярно, то есть под прямым углом к основанию. А биссектриса – это линия, которая выходит из вершины треугольника и делит ее угол ровно пополам.

Кстати, присмотритесь к рисунку. С помощью медиан в любом треугольнике образуются внутренние маленькие треугольники. Так вот, в равносторонней фигуре они равны между собой как по длине сторон, так и по площади.

Медиана прямоугольного треугольника

Прямоугольный треугольник, если кто забыл, это треугольник, у которого один угол составляет 90 градусов. И в такой фигуре медиана тоже обладает уникальными свойствами.

Но речь идет только о той медиане, которая выходит из прямого угла. Так вот, ее длина равна половине длины гипотенузы. Так называют самую длинную сторону прямоугольного треугольника.

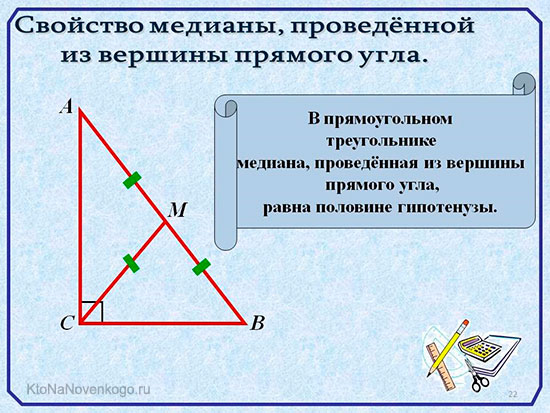
Соответственно, при решении задач правдиво будет и обратное условие. Так, если указано, что отрезок СМ в нашем примере равен АВ/2, или равен отдельно АМ и ВМ, то можно смело делать вывод, что перед нами прямоугольный треугольник.

Вместо заключения

А теперь вернемся к тому, о чем мы говорили в самом начале статьи. Термин МЕДИАНА имеет несколько значений.

Например, а в статистике медианой называют уровень показателей, который делит все данные на две равные половины.

И наконец, в Сербии есть археологический памятник, который называется Медиана. Так назвалась древнеримская вилла, руины которой находятся в городе Неш. Она уникальна тем, что была построена при императоре Константине в 300 году и была его резиденцией, в которой он принимал почетных гостей.

Вот и все, что мы хотели рассказать о МЕДИАНЕ. До новых встреч на страницах нашего блога.

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Теперь остаётся подумать над тем, как применить это знание о медиане на практике. Если придумаю, вдруг Нобелевскую премию дадут?

Определение медианы треугольника
Свойства медианы
- Свойство 1 (основное)
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.
- AC – самая длинная сторона, следовательно, медиана BF – самая короткая.
- AB – самая короткая сторона, следовательно, медиана CD – самая длинная.
Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 1
Площадь одной из фигур, образованной в результате пересечения трех медиан в треугольнике, равняется 5 см 2 . Найдите площадь треугольника.

Решение
Согласно свойству 3, рассмотренному выше, в результате пересечения трех медиан образуются 6 треугольников, равных по площади. Следовательно:
S_△ = 5 см 2 ⋅ 6 = 30 см 2 .

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Отрезок \(AC\) называется перпендикуляром, проведённым из точки \(A\) прямой \(a\), если прямые \(AC\) и \(a\) перпендикулярны.

Докажем, что от точки \(A\), не лежащей на прямой \(BC\), можно провести перпендикуляр к этой прямой.

Отложим от луча \(BC\) угол, равный данному, и совместим эти углы накладыванием (представим, что сложим лист бумаги с равными углами по стороне \(BC\)).

Прямая AA 1 перпендикулярна прямой \(BC\), а отрезок \(AC\) является перпендикуляром от точки \(A\) к прямой \(BC\).

Если допустить, что через точку \(A\) можно провести ещё один перпендикуляр к прямой \(BC\), то он бы находился на прямой, пересекающейся с AA 1 . Но две к одной и той же прямой перпендикулярные прямые должны быть параллельны и не могут пересекаться.

Это противоречие, что означает: через данную точку к прямой можно провести только один перпендикуляр.

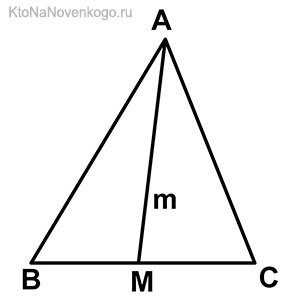
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

Поэтому для построения медианы необходимо выполнить следующие действия:
1. найти середину стороны;
2. соединить точку, являющуюся серединой стороны треугольника, с противолежащей вершиной отрезком — это и будет медиана.

Биссектриса треугольника — это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне.

Поэтому для построения биссектрисы необходимо выполнить следующие действия:
1. построить биссектрису какого-либо угла треугольника (биссектриса угла — это луч, выходящий из вершины угла и делящий его на две равные части );
2. найти точку пересечения биссектрисы угла треугольника с противоположной стороной;
3. соединить вершину треугольника с точкой пересечения на противоположной стороне отрезком — это и будет биссектриса треугольника.

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону.

Поэтому для построения высоты необходимо выполнить следующие действия:
1. провести прямую, содержащую одну из сторон треугольника ( в случае, если проводится высота из вершины острого угла в тупоугольном треугольнике );
2. из вершины, лежащей напротив проведённой прямой, опустить перпендикуляр к ней ( перпендикуляр — это отрезок, проведённый из точки к прямой, составляющей с ней угол 90 ° ) — это и будет высота.

Но, как выше упомянуто, для некоторых видов треугольников построение высот и точки их пересечения отличаются.

Если треугольник с прямым углом, то стороны, образующие прямой угол, можно назвать высотами, так как они перпендикулярны одна к другой. Точкой пересечения высот является общая вершина перпендикулярных сторон.

Если треугольник с тупым углом, то высоты, опущенные с вершин острых углов, выходят вне треугольника к продолжениям сторон. Прямые, на которых расположены высоты, пересекаются вне треугольника.

Если из одной и той же вершины провести медиану, биссектрису и высоту, то медиана окажется самым длинным отрезком, а высота — самым коротким отрезком.

Сегодня мы рассмотрим часть треугольника, которая не раз поможет тебе при решении многих задач, — медиану.

Эта приятная, лёгкая и полезная теория!

Медиана треугольника — коротко о главном

Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медиана делит площадь треугольника пополам

Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении \( \displaystyle 2:1\ \), считая от вершины.

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Если медиана равна половине стороны, то треугольник прямоугольный и эта медиана проведена к гипотенузе.

Определение медианы треугольника

Это очень просто! Возьми треугольник.

Отметь на какой-нибудь его стороне середину \( \displaystyle M\).

И соедини с противоположной вершиной!

Получившийся отрезок \( \displaystyle BM\) и есть медиана.

Медиана треугольника – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Медиана в прямоугольном треугольнике

Медиана равна половине гипотенузы прямоугольного треугольника!

Почему. При чём тут прямой угол?

Давай смотреть внимательно. Только не на треугольник, а на … прямоугольник.

Ты заметил, что наш треугольник \( \displaystyle ABC\) – ровно половина этого прямоугольника?

Проведём диагональ \( \displaystyle BD\):

Помнишь ли ты, что диагонали прямоугольника равны и делятся точкой пересечения пополам?

Но одна из диагоналей – \( \displaystyle AC\) – наша гипотенуза! Значит, точка пересечения диагоналей – середина гипотенузы \( \displaystyle \Delta ABC\).

Она называлась у нас \( \displaystyle M\).

Значит, половина второй диагонали – наша медиана \( \displaystyle BM\). Диагонали равны, их половинки, конечно же, тоже. Вот и получим \( \displaystyle BM=MA=MC\)

Медиана в прямоугольном треугольнике, проведенная к гипотенузе, равна половине гипотенузы.

Более того, так бывает только в прямоугольном треугольнике!

Если медиана равна половине стороны, то треугольник прямоугольный, и эта медиана проведена к гипотенузе.

Доказывать это утверждение мы не будем, а чтобы в него поверить, подумай сам: разве бывает какой-нибудь другой параллелограмм с равными диагоналями, кроме прямоугольника?

Нет, конечно! Ну вот, значит, и медиана может равняться половине стороны только в прямоугольном треугольнике.

Решение задач на свойства медианы в прямоугольном треугольнике

Давай посмотрим, как это свойство помогает решать задачи.

Задача №1:

В \( \displaystyle \Delta ABC\) стороны \( \displaystyle AC=5\); \( \displaystyle BC=12\). Из вершины \( \displaystyle C\) проведена медиана \( \displaystyle CN\).

Найти \( \displaystyle AB\), если \( \displaystyle AB=2CN\).

Сразу вспоминаем, это если \( \displaystyle CN=\frac\), то \( \displaystyle \angle ACB=90<>^\circ \)!

Ура! Можно применить теорему Пифагора!

Видишь, как здорово? Если бы мы не знали, что медиана равна половине стороны только в прямоугольном треугольнике, мы никак не могли бы решить эту задачу. А теперь можем!

Применяем теорему Пифагора:

А в следующей задаче пусть у нас будет не одна, а целых три медианы! Как же они себя ведут?

Запомни очень важный факт:

Три медианы в треугольнике (любом!) пересекаются в одной точке и делятся этой точкой в отношении \( 2:1\), считая от вершины.

Сложно? Смотри на рисунок:

Медианы \( \displaystyle AM\), \( \displaystyle BN\) и \( \displaystyle CK\) пересекаются в одной точке.
- \( \displaystyle AO\) – вдвое больше, чем \( \displaystyle OM\);
- \( \displaystyle BO\) – вдвое больше, чем \( \displaystyle ON\);
- \( \displaystyle CO\) – вдвое больше, чем \( \displaystyle OK\).
Задача №2:

В треугольнике \( \displaystyle ABC\) проведены медианы \( \displaystyle BM\) и \( \displaystyle AK\), которые пересекаются в точке \( \displaystyle O\). Найти \( \displaystyle BO\), если \( \displaystyle AB=3;\text< >BC=4,\text< >\angle B=90<>^\circ .\)

Решение:

\( \displaystyle \angle B=90<>^\circ \) – треугольник прямоугольный!

(Применили то, что медиана, проведённая к гипотенузе равна половине гипотенузы).

Найдём \( \displaystyle AC\) по теореме Пифагора:

Читать далее…

Мы хотим постоянно улучшать этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)

Теорема о медиане и площади треугольника

Медиана делит площадь треугольника пополам

Почему? А давай вспомним самую простую форму площади треугольника. \( S=\fraca~\cdot h\).

И применим эту формулу аж два раза!

Посмотри, медиана \( \displaystyle BM\) разделила \( \displaystyle \triangle ABC\) на два треугольника: \( \displaystyle \triangle ABM\) и \( \displaystyle \triangle BMC\).

Но! Высота-то у них одна и та же – \( \displaystyle BH\)!

Только в \( \displaystyle \triangle ABM\) эта высота \( \displaystyle BH\) опускается на сторону \( \displaystyle AM\), а в \( \displaystyle \triangle BMC\) – на продолжение стороны \( \displaystyle CM\).

Удивительно, но вот бывает и так: треугольники разные, а высота – одна. И вот, теперь-то и применим два раза формулу

1) B \( \displaystyle \triangle ABM\):

2) B \( \displaystyle \triangle BMC\):

Запишем ещё раз:

Читать далее…

Мы хотим постоянно улучшать этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)

Теорема о трех медианах треугольника

Три медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении \( \displaystyle 2:1\ \), считая от вершины.

Что бы это такое значило? Посмотри на рисунок. На самом деле утверждений в этой теореме целых два. Ты это заметил?

1. Медианы треугольника пересекаются в одной точке.

2. Точкой пересечения медианы делятся в отношении \( \displaystyle 2:1\ \), считая от вершины.

Давай попробуем разгадать секрет этой теоремы, то есть доказать ее.

Доказательство теоремы о трех медианах треугольника

Сначала проведем не все три, а только две медианы. Они-то уж точно пересекутся, правда? Обозначим точку их пресечения буквой \( \displaystyle E\).

Соединим точки \( \displaystyle N\) и \( \displaystyle K\). Что получилось?

Конечно, \( \displaystyle NK\) – средняя линяя \( \displaystyle \triangle ABC\). Ты помнишь, что это значит?
- \( \displaystyle NK\) параллельна \( \displaystyle AC\);
- \( \displaystyle NK=\frac\).
А теперь проведем ещё одну среднюю линию: отметим середину \( \displaystyle AE\) – поставим точку \( \displaystyle F\), отметим середину \( \displaystyle EC\) — поставим точку \( \displaystyle G\).

Теперь \( \displaystyle FG\) – средняя линия \( \displaystyle \triangle AEC\). То есть:
- \( \displaystyle FG\) параллельна \( \displaystyle AC\);
- \( \displaystyle FG=\frac\).
Заметил совпадения? И \( \displaystyle NK\) , и \( \displaystyle FG\) – параллельны \( \displaystyle AC\). И \( \displaystyle NK=\frac\), и \( \displaystyle FG=\frac\).

Что из этого следует?
- \( \displaystyle NK\) параллельна \( \displaystyle FG\);
- \( \displaystyle NK=FG\)
Посмотри теперь на четырехугольник \( \displaystyle NKGF\). У какого четырехугольника противоположные стороны (\( \displaystyle NK\) и \( \displaystyle FG\)) параллельны и равны?

Конечно же, только у параллелограмма!

Значит, \( \displaystyle NKGF\) – параллелограмм. Ну и что?

А давай вспомним свойства параллелограмма. Например, что тебе известно про диагонали параллелограмма? Правильно, они делятся точкой пересечения пополам.

Снова смотрим на рисунок.

Читать далее…

Мы хотим постоянно улучшать этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)

Формула длины медианы треугольника

Как же найти длину медианы, если известны стороны? А ты уверен, что тебе это нужно?

Откроем страшную тайну: эта формула не очень полезная. Но всё-таки мы её напишем, а доказывать не будем.

Бонусы: Вебинары из нашего курса подготовки к ЕГЭ по математике по треугольникам

Лучше всего смотреть это видео с ручкой и тетрадкой в руках. То есть ставьте видео на паузу и решайте задачи самостоятельно.

Помните, понимать и уметь решать — это два, совершенно разных навыка. Очень часто вы понимаете как решить задачу, но не можете это сделать. Или допускаете ошибки, или просто теряетесь и не можете найти ход решения.

Нужно решать много задач. Другого способа нет. Вы должны совершить свои ошибки, чтобы научиться их не допускать.

ЕГЭ №6 Равнобедренный треугольник, произвольный треугольник

ЕГЭ №6 Прямоугольный треугольник, теорема Пифагора, тригонометрия

Большинство задач в планиметрии решается через прямоугольные треугольники. Как это так? Ведь далеко не в каждой задаче речь идёт о треугольниках вообще, не то что прямоугольных.

Но на уроках этой темы мы убедимся, что это действительно так. Дело в том, что редкая сложная задача решается какой-то одной теоремой — почти всегда она разбивается на несколько задач поменьше.

И в итоге мы имеем дело с треугольниками, зачастую — прямоугольными.

В этом видео мы научимся решать задачи о прямоугольных треугольниках из ЕГЭ, выучим все необходимые теоремы и затронем основы тригонометрии.

ЕГЭ №16. Подобие треугольников. Задачи н доказательство

Это одна из самых сложных задачи в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!

Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства. Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.

В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.

Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.

Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.

Читайте также:

Что такое медиана треугольника кратко

Определение и свойства медианы треугольника

Определение медианы треугольника