Чему равны координаты координатных векторов кратко
Обновлено: 04.07.2024
В прямоугольной системе координат х0у проекции х и у вектора AB на оси абсцисс и ординат называются координатами вектора. Свойства координат вектора. Формула определения координат вектора для пространственных задач.
В прямоугольной системе координат х0у проекции х и у вектора на оси абсцисс и ординат называются координатами вектора. Координаты вектора общепринято указывать в виде (х, у), а сам вектор как: =(х, у).
Формула определения координат вектора для двухмерных задач.
В случае двухмерной задачи вектор с известными координатами точек A(х1;у1) и B(x2;y2) можно вычислить:
= (x2 – x1 ; y2 – y1).
Формула определения координат вектора для пространственных задач.
В случае пространственной задачи вектор с известными координатами точек A(х1;у1;z1) и B(x2;y2;z2) можно вычислить применив формулу:
= (x2 – x1 ; y2 – y1;z2 – z1).
Координаты дают всеобъемлющую характеристику вектора, поскольку по координатам есть возможность построить и сам вектор. Зная координаты, легко вычислить и длину вектора. (Свойство 3, приведенное ниже).
Свойства координат вектора.
1. Любые равные векторы в единой системе координат имеют равные координаты.
2. Координаты коллинеарных векторов пропорциональны. При условии, что ни один из векторов не равен нулю.
3. Квадрат длины любого вектора равен сумме квадратов его координат.
4.При операции умножения вектора на действительное число каждая его координата умножается на это число.
5. При операции сложения векторов вычисляем сумму соответствующие координаты векторов.
6. Скалярное произведение двух векторов равняется сумме произведений их соответствующих координат.
Вектором называется направленный отрезок, один из концов которого является началом, а другой − концом вектора.
Единичные векторы
Единичные векторы трехмерной декартовой системы координат обозначаются следующим образом:
\( \mathbf = \left( \right) \) ,
\( \mathbf = \left( \right) \) ,
\( \mathbf = \left( \right) \) ,
\( \left| \mathbf \right| = \left| \mathbf \right| = \left| \mathbf \right| = 1 \) .
Данная тройка единичных векторов образует базис координатной системы.
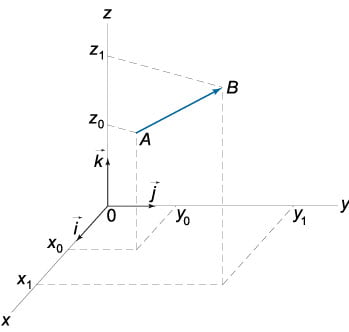
Любой вектор можно разложить по базисным векторам. Формула разложения записывается в виде :
\( \mathbf = \mathbf = \left( - > \right)\mathbf + \left( - > \right)\mathbf + \left( - > \right)\mathbf. \)
Длиной (или модулем ) вектора называется расстояние между началом и концом вектора
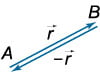
Противоположные векторы имеют равные длины и направлены в противоположные стороны:
Если \( \mathbf = \mathbf \) , то \( \mathbf = -\mathbf \) .
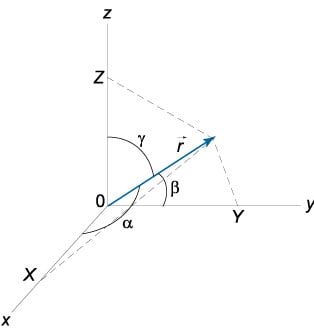
Координатами вектора называются проекции вектора на оси координат:
\( X = \left| \mathbf \right|\cos \alpha \) , \( Y = \left| \mathbf \right|\cos \beta \) , \( Z = \left| \mathbf \right|\cos \gamma. \)
Величины \( \cos\alpha \) , \( \cos\beta \) , \( \cos\gamma \) являются направляющими косинусами вектора \( \mathbf \) .
Векторы называются коллинеарными , если они параллельны одной и той же прямой.
Векторы являются равными , если они коллинеарны, одинаково направлены и имеют равные длины. У равных векторов соответствующие координаты также равны:
Если \( \mathbf\left( \right) = \mathbf\left( ,,> \right) \) , то
\( X = \) , \( Y = \) , \( Z = \) .
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Вспомним, что при умножении вектора на число k ≠ 0 мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если k > 0 , или противоположно направлены, если k 0 . Длины векторов различаются \(k\) раз.
Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде c → = k ⋅ a → + m ⋅ b → . Говорят, что вектор c → разложен по векторам a → и b → , а числа \(k\) и \(m\) называют коэффициентами разложения .
Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.

Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают i → и j → .

Если от начала координат отложить вектор a → , то его можно разложить по векторам i → и j → следующим образом: a → = 3 ⋅ i → + 2 ⋅ j → .
Любой вектор, который равен с вектором a → , можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.
Но в то же время в координатной системе можно переместить векторы i → и j → , таким образом определить координаты векторов независимо от их места расположения в координатной системе.
Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.
Связь между координатами противоположных векторов следует из того, что, если умножить вектор на \(-1\), результатом будет противоположный вектор.
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Координаты вектора
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $\overline$, начало которого совпадает с началом системы координат (рис. 1).
Сумма двух векторов, заданных координатами
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.

Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Умножение вектора на число
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $A\left(a_ ; a_\right)$ и $B\left(b_ ; b_\right)$. Тогда координаты вектора $\overline=\left(x_ ; y_\right)$ находятся по формулам (рис. 4):
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.
Задание. Найти координаты вектора $\overline$, если $A(-4 ; 2), B(1 ;-3)$
Решение. $\overline=(1-(-4) ;-3-2)=(5 ;-5)$
Направляющие косинусы
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.
Здесь $\alpha$, $\beta$ и $\gamma$ - углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.
Читайте также:

