Сообщение о дирихле и о задачах решаемых с помощью его принципа
Обновлено: 15.05.2024
Однажды на уроке математики учитель показала нам решение одной задачи с элементами доказательства. При этом она ссылалась на принцип Дирихле. Я заинтересовалась этим доказательством, ученым, который ввел его в математику ,стала находить и решать задачи с применением этого способа доказательства.
Самым интересным и сложным было находить в казалось бы простых задачах "зайцев" и "клетки",т. к. это иногда было совсем не очевидно. Из-за неправильного выбора задачи не решались ,а как только определялись "зайцы" и "клетки" , принцип Дирихле сразу помогал их решать.
После того, как я изучила этот принцип доказательства ,я сама стала придумывать несложные задачи, решаемые с помощью принципа Дирихле. Так создавалась работа, которую я представляю.
С этой работой я выступала перед учениками моего класса и думаю, что решение подобных задач заинтересовало их , так как многие из них с удовольствием решали задачи, составленные мной , и решали их правильно.
Принцип Дирихле утверждает, что если множество из N элементов разбито на n непересекающихся частей, не имеющих общих элементов , где N > n ,то по крайней мере в одной части будет более одного элемента.
Самая популярная формулировка принципа Дирихле такова:
"Если в n клетках сидит N зайцев , причем N > n , то хотя бы в одной клетке сидят по крайней мере два зайца.
Принцип Дирихле представляет собой настолько очевидное утверждение, что на первый взгляд даже непонятно, почему он является весьма эффективным методом решения задач. Дело в том, что в каждой конкретной задаче нелегко бывает понять, что же здесь "зайцы" и "клетки" и почему зайцев больше, чем клеток. Выбор зайцев и клеток часто неочевиден ; далеко не всегда по виду задачи можно определить, что следует воспользоваться принципом Дирихле.
Авторские задачи, решаемые с помощью принципа
К Новому Году в детском саду ребята делали фонарики. В группе 30 детей. Петя Пяточкин сделал 12 фонариков, а остальные – меньше. Докажите, что хотя бы три ребенка сделали одинаковое количество фонариков (может быть, по 0 шт. ).
Здесь “зайцы”- дети ,а “клетки” - число сделанных фонариков. В клетку 0 “посадим” всех, кто не сделал ни одного фонарика ,в клетку 1- тех, у кого од ин фонарик ,в клетку
2- два фонарика,и так до клетки 12 ,куда
П опал Петя Пяточкин. Применим принцип
Дирихле. Докажем утверждение за д ачи от противного. Предположим , никакие три ребенка не сделали по одинаковому числу фонариков ,то есть в каждую из клеток 0,1,. ,11 попало мен ьше трех детей. Тогда в каждой из них два челов ека или меньше, а всего в этих 12 клетках не больше 24 человек. Добавив Петю Пяточкина, все равно не наберем 30 ребят. Получили противоречие.
Может быть и такое, что кроме Пети вообще никто не сделал ни одного фонарика ,то есть сделал по 0 штук.
В научно-исследовательском институте 33 отдела. Всего работает 1150 человек. Найдется ли отдел, в котором меньше 35 сотрудников?
Допустим,что в каждом отделе работает по 35 сотрудников. Тогда общее число сотрудников будет : 35 х 33 = 1155 человек , что противоречит условию. Следовательно , если в 32 отделах р аботает по 35 человек, то 35 х 32 = 1120 человек , и в 33-м отделе будет только 30 человек. Поэтому, хотя бы в одном отделе работает менее 35 человек.
На свой юбилей отец пригласил 25 сослуживцев. Известно,что среди любых трех из них есть двое знакомых друг с другом. Докажите,что есть такой гость,у которого не менее 2 знакомых.
Выберем любых двух гостей, которые не знакомы между собой. ( Если таких нет,то все гости знакомы между собой
,значит,у каждого имеется 24 знакомых, и задача решена).
Из оставшихся 23 гостей каждый знаком с одним из этих двух,иначе мы имели бы тройку гостей,среди которых не было бы знакомых. Тогда у одного из выбранны х двух гостей не менее12 з на к ом ых (23 "зайца" рассажены в двух "клетках").
За пять лет дачники вырастили и собрали 31 кг. черной смородины. Причем каждый год они собирали урожай больший,чем в предыдущем году. На пятом году они собрали ягод втрое больше,чем в первый год. Какой был урожай смородины на четвертый год?





ПРИНЦИП ДИРИХЛЕ

Автор работы награжден дипломом победителя III степени
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF
Введение
Объектом моих исследований являются способы и методы решения логических задач. Логическая задача – это особый вид задачи, который развивает логику, образное и творческое мышление, поэтому часто такие задачи являются олимпиадными. Решение таких задач увлекательное занятие, поскольку для решения большинства из них требуется не только знание определенного программного материала, но и логическое мышление. Я уже рассматривал применение кругов Эйлера и задачи на шахматной доске.
Разнообразие логических задач велико, велико и количество способов их решения. При решении многих задач я столкнулся с еще одним методом рассуждения — "от противного". Меня заинтересовала одна из его форм — принцип Дирихле. Способ решения задач с помощью данного принципа я сделать предметом исследования данной работы.
Гипотеза: принцип Дирихле позволяет решать некоторые логические задачи, которые сложно решать другими способами.
Цель работы:
исследование эффективности применения принципа Дирихле в решении задач;
получение знаний о применении и сферах использования принципа Дирихле.
В ходе выполнения работы мной были решены следующие задачи:
изучить литературу и собрать информацию о принципе Дирихле;
отобрать и систематизировать задачи, решаемые с помощью принципа Дирихле;
научиться самостоятельно решать задачи данным методом.
Мной использовались следующие методы исследования:
Моя работа весьма актуальна, так как принцип Дирихле не рассматривается в учебниках математики, а полученные знания пригодятся для сдачи экзаменов и решении практических задач в жизни.
I. Общая информация о принципе Дирихле
I. 1. Биография Дирихле
В 1825 г. Дирихле вместе с А. Лежандром доказал великую теорему Ферма для частного случая n=5. В 1827 занял место доцента в Бреславе; с 1829 работал в Берлине. В 1831-1855гг. – профессор Берлинского университета, после смерти К. Гаусса (1855г.) – Гёттингенского университета.
Сделал ряд крупных открытий в теории чисел; установил формулы для числа классов бинарных квадратичных форм с заданным определителем и доказал теорему о бесконечности количества простых чисел в арифметической прогрессии из целых чисел, первый член и разность которой взаимно просты. К решению этих задач применил аналитические функции, названные функциями (рядами) Дирихле. Создал общую теорию алгебры, единиц в алгебраическом числовом поле. В области математического анализа впервые точно сформулировал и исследовал понятие условной сходимости ряда, дал строгое доказательство возможности разложения в ряд Фурье кусочно-непрерывной и монотонной функций, что послужило обоснованием для многих дальнейших исследований. Значительны труды Дирихле в механике и математической физике, в частности, в теории потенциала. С именем Дирихле связаны задача, интеграл (ввел интеграл с ядром Дирихле), принцип, характер, ряды. Лекции Дирихле имели огромное влияние на выдающихся математиков более позднего времени, в том числе на Г. Римана, Ф. Эйзенштейна, Л. Кронекера, Ю. Дедекинда.
I. 2. Различные формулировки принципа Дирихле
При решении многих задач используется логический метод рассуждения — "от противного". Здесь мы рассмотрим одну из его форм — принцип Дирихле. Этот принцип утверждает, что если множество из n элементов разбито на m непересекающихся частей, не имеющих общих элементов, где n > m то, по крайней мере, в одной части будет более одного элемента.
На языке отображений эта формулировка означает, что если в А (множестве предметов) больше элементов, чем в В (множестве ящиков), то не существует обратимого отображения А в В.
Другая формулировка “ принципа Дирихле“: если n + 1 предмет поместить в n мест, то обязательно хотя бы в одном месте окажутся хотя бы два предмета.
В шутливой форме принцип Дирихле выглядит так: “нельзя посадить семерых зайцев в три клетки так, чтобы в каждой клетке находилось не больше двух зайцев “.
Заметим, что в роли кроликов могут выступать различные предметы и математические объекты - числа, отрезки, места в таблице и т. д. Если мы хотим применить принцип Дирихле при решении конкретной задачи, то нам предстоит разобраться, что в ней — "клетки", а что — "кролики". Это обычно является самым трудным этапом в доказательстве.
I. 3. Обобщение принципа Дирихле
Если nk+1 зайцев размещены в n клетках, то найдутся k+1 зайцев, которые посажены в одну клетку (n, k - натуральные числа).
Обобщенный принцип Дирихле также достаточно очевиден: если бы в каждой клетке сидело не более k зайцев, то во всех клетках было бы не более nk зайцев, что противоречит условию. Обобщение принципа используют, когда требуется выявить несколько (три и более) объектов, обладающих некоторым свойством.
В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Докажите, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта. Решение.
II. Применение принципа Дирихле для решения различных задач
II. 1. Принцип Дирихле и арифметика
Задача 2. В школе 400 учеников. Докажите, что хотя бы двое из них родились в один день года.
Решение: 400 > 366.
Задача 3. В классе 40 учеников. Найдётся ли такой месяц в году, в котором отмечают свой день рождения не меньше чем 4 ученика этого класса?
Решение: Рассуждаем от противного. Если бы такого месяца не нашлось, то в каждом из 12 месяцев день рождения отмечали бы не более трёх учеников. Значит, всего учеников было бы не более 12 · 36. Но 40 > 36. Противоречие.
II. 2. Принцип Дирихле в теории чисел
Возможна следующая переформулировка принципа Дирихле:
"Среди p + 1 целых чисел найдутся два числа, дающие при делении на p один и тот же остаток".
При делении с остатком на p может встретиться конечное число различных остатков: 0, 1, 2, . . . , p-1. Они то и играют здесь роль "клеток", а сами целые числа являются "зайцами". Так как чисел ("зайцев") больше, чем остатков ("клеток"), то хотя бы два числа "сидят в одной клетке", т.е. имеют одинаковые остатки при делении на p. Рассмотрим классические примеры.
Задача 1. Дано 11 различных целых чисел. Доказать, что из них можно выбрать два числа, разность которых делится на 10.
Решение: По крайней мере два числа из 11 дают одинаковый остаток при делении на 10 (принцип Дирихле). Пусть это будут A = 10a + r и B = 10b + r. Тогда их разность делится на 10: A - B = 10(a - b).
Задача 2. Из любых трёх целых чисел можно выбрать два, сумма которых чётна. Докажите это.
Решение: Все числа можно разбить на два класса: чётные и нечётные. Невозможно распределить три числа по двум классам так, чтобы ни в какой класс не попало более одного числа. Значит, среди любых трёх целых чисел найдутся два числа одинаковой чётности. Их сумма чётна.
II. 3. Принцип Дирихле и геометрия
Задача 1. В квадрат со стороной 1 метр бросили 51 точку. Докажите, что какие-то три из них можно накрыть квадратом со стороной 20 см.
Решение: Разобьем наш квадрат на 25 квадратов со стороной 20 см. По обобщенному принципу Дирихле, в какой-то из них попадёт, по крайней мере, три точки из 51 брошенной.
Задача 2. Внутри равностороннего треугольника со стороной 1см расположено 5 точек. Докажите, что расстояние между некоторыми двумя из них меньше 0,5см.
Задача 3. В квадрате площадью S расположено 100 фигур, сумма площадей которых больше 99S. Доказать, что у всех этих фигур есть общая точка. Решение. Пусть S1, S2, . . . , S100 - площади данных фигур, а , …, - площади фигур, дополняющих их до квадрата. Понятно, что . По условию S1+S2+. . .+S100 > 99S, поэтому
+ + … + = (S- S1)+ (S- S2)+. . .+ (S- S100) = 100S-(S1+ S2+. . .+ S100) 2 уравнение xn + yn = zn (уравнение Ферма) не имеет решений в целых ненулевых числах x, y, z. Теорема была сформулирована Пьером Ферма примерно в 1630 году на полях книги Диофанта "Арифметика"
Теория чисел, или высшая арифметика — раздел чистой математики, изучающий свойства натуральных и целых чисел.
Чётное число — целое число, которое делится на 2 без остатка: …−4,−2,0,2,4,6,8,10.

Математические олимпиады являются одной из форм внеклассной работы и массовым соревнованием учащихся. На олимпиадах учащиеся показывают свой уровень знаний в области математики. Олимпиады способствуют повышению интереса учащихся к предмету. Задачи для своего решения требуют сообразительности и умения рассуждать.
Подготовка учащихся к решению олимпиадных задач является одной из функций учителя математики. Но вместе с тем учителям общеобразовательных школ не хватает современной методической литературы, предназначенной для работы с более способными учащимися по организации и проведению кружковых занятий, олимпиад по математике. Учителя готовят учащихся к олимпиадам, опираясь на свой собственный опыт и обычно работа ведется на эмпирическом уровне без теоретической основы.
Решение задач является компонентом подготовки к олимпиадных задач. правило, у логической имеется единственный . Существует множество решения этих и одним из является принцип . Так как рассмотрение не школьной программой, существуют дополнительные занятия для подготовки к олимпиадам и курсы по выбору, где и рассматривается данный способ решения.
Принцип Дирихле начинают рассматривать уже в 5-ом классе, но пока только в игровой форме. В учебниках по математике для 5-11 классов, принцип Дирихле упоминается лишь в одном - по алгебре за 8 класс под редакцией Н. Я. Виленкина, А. Н. Виленкина и др. [19, 1, 16, 7, 8].
Принцип Дирихле берёт своё начало в комбинаторике, на данный же момент этот принцип используется в разных областях математики, таких как геометрия, арифметика и теория чисел. Автором данного принципа является Дирихле Петер Густав Лежён (13.02.1805 – 05.05.1859) – немецкий математик, внёсший существенный вклад в математическую науку. Родился он в Дюрене. С 1822 г. по 1827 г. работал учителем в доме генерала Фуа, у которого и проживал эти годы. В свободное время Дирихле посещал лекции во французском колледже для изучения научных трудов других математиков. В Париже Лежён Дирихле знакомится с уже известными учёными. Нахождение в кругу таких людей пробудило в нём исследовательский интерес и послужило мотивом для его дальнейшей деятельности в математической сфере. В 1855 году он получает звание профессора высшей математики в университете Гёттингена. У Дирихле много крупных открытий в самых разных областях математики, а также в механике и математической физике. Он вывел множество формул и принципов решения задач. Один из называется - Принцип - это утверждение, сформулировал Дирихле в 1834 .
Объект исследования – методы решения олимпиадных задач.
Предмет исследования – принцип Дирихле.
Цель – изучить принцип Дирихле и научиться применять его для решения задач.
Работа состоит из введения, теоретической части, в которой два параграфа, практической части, в которой четыре параграфа и заключения. Список использованной литературы включает в себя 23 наименования.
Глава Ι. Основные сведения о принципе Дирихле
История создания принципа Дирихле
В 1899 года Давид Гильберт обратился к одной старой знаменитой проблеме, известной как принцип Дирихле. Суть этой проблемы составляла одна логическая трудность, на которую стали внимание только времен Вейерштрасса. , Дирихле, Риман и математики выдвигали о том, что существует решение называемой краевой для уравнения . Это предположение основано на , позволяющей всегда , что в соответствующей реальной ситуации, описываемой этой краевой задачей, должен быть определенный физический результат, а значит и решение. Кроме того, с математической стороны Гаусс заметил, что краевая задача для этого же уравнения может быть сведена к задаче минимизации некоторого двойного интеграла от функций с непрерывными частными производными, имеющих заданные граничные значения. В силу положительности этого двойного интеграла, очевидно, должна была существовать наибольшая нижняя грань для его значений, из чего он делал вывод, что для одной из рассматриваемых функций этот интеграл принимал значение этой грани. Рассуждение такого рода стало известно под названием принципа Дирихле.
Но позже критикой данного утверждения занялся Карл Вейерштрасс [20]. Как указывал Вейерштрасс, предположение о том, что среди допустимых функций должна существовать та, на которой интеграл принимает наименьшее значение, не является обоснованным с математической точки зрения. Более того Вейерштрасс построил пример, в котором нельзя было найти функции, минимизирующей интеграл, при заданных граничных значениях. Можно подумать, что на этом принцип провалился, но . В сентябре 1899 года смог представить математическому обществу попытку того, он назвал " принципа Дирихле" [10]. Гильберта была в , что при сильных ограничениях функции, участвовавшие в , можно добиться , что принцип будет выполняться.
тема очень в наши дни. Так как роль олимпиад растёт, а знание принципа Дирихле очень помогает при решении олимпиадных задач. Так же он используется в разных областях математики и в повседневной жизни.
Таким образом, мы познакомились с историей создания данного принципа. Изучением принципа Дирихле занимались такие учёные как Давид Гильберт, Вейерштрасс, Гаусс и Риман. А также, выяснили какую связь устанавливает Дирихле в своём принципе.
1.2 Формулировки принципа Дирихле
На первый взгляд принцип Дирихле является очевидным утверждением, но несмотря на его очевидность и , он часто во время задач и доказательства в различных областях . Заслуга Дирихле том, что сформулировал очевидное , а в том, что первым заметил, с такого простого можно получить результаты.
Разных формулировок принципа Дирихле много. И в зависимости от типа задачи нужно найти подходящую формулировку для решения.
Доказательство. Предположим, что не найдётся такой клетки. Значит, в каждой клетке находится не более чем k зайцев. Тогда в n клетках не более чем k * n зайцев. Но по условию у нас было k * n + 1 зайцев. Получилось противоречие, а значит наше предположение неверно. Из этого следует, что найдется хотя бы одна клетка, в которой находятся не менее чем k + 1 заяц.
Изучив теоретическую основу по данной теме, можно рассмотреть примеры задач, в которых используется принцип Дирихле.
Глава ΙΙ. Применение принципа Дирихле к решению задач
Мы рассмотрели и систематизировали задачи с использованием принципа Дирихле на 4 группы. Задачи в комбинаторике, в арифметике, в теории чисел и в геометрии.
2.1 Решение арифметических задач
1. В классе 30 учеников. Ваня сделал в контрольной работе 13 ошибок, а остальные допустили меньшее количество ошибок. Докажите, что по крайней мере 3 ученика сделали равное количество ошибок.
2. В лесу растет миллион ёлок. Известно, что на каждой из них не более 600000 иголок. Докажите, что найдутся две ёлки с одинаковым числом иголок.
3. В школе 450 учеников. Докажите, что, хотя бы двое из них родились в один день года.
4. В классе 40 учеников. Докажите, что найдётся такой месяц в году, в котором отмечают свой день рождения не меньше чем 4 ученика этого класса.
Доказательство. Рассуждаем от противного. Если бы такого месяца не нашлось, то в каждом из 12 месяцев день рождения отмечали бы не более трёх учеников. Значит, всего учеников было бы не более 12*3=36. Но по условию у нас 40 учеников, а значит найдётся такой месяц в году, котором отмечают свой день рождения не меньше чем 4 ученика этого класса.
5. В магазин привезли 25 ящиков с тремя разными сортами яблок (в каждом ящике яблоки только одного сорта). Докажите, что среди них есть по крайней мере 9 ящиков с яблоками одного и того же сорта.
6. В городе N живет 3 миллиона человек. Докажите, что у каких-то двух из них одинаковое число волос на голове, если известно, что у любого человека на голове миллион волос.
7. Сто человек сидят за круглым столом, причем более половины из них – мужчины. Докажите, что какие-то два мужчины сидят друг напротив друга.
В данном параграфе мы рассмотрели выше представленные задачи и вывели следующую особенность: для решения задач данного типа нужно выполнить арифметические действия.
2.2 Решение задач из теории чисел
1. Докажите, что из любых трёх целых чисел можно выбрать два, сумма которых чётна.
Доказательство. Все числа можно разбить на два класса: чётные и нечётные. Невозможно распределить три числа по двум классам так, чтобы ни в какой класс не попало более одного числа. Значит, среди любых трёх целых чисел найдутся два числа одинаковой чётности. А сумма чётных чисел чётна.
2. Доказать, что среди 101 целого числа всегда можно выбрать два таких, что их разность делится на 100.
Доказательство. При делении на 100 возможны 100 различных остатков: 0, 1, 2, . , 99. Среди 101 остатка, полученных после деления 101 числа на 100, найдётся, два одинаковых. Разность этих двух чисел при делении на 100 имеет остаток 0, из этого следует, что оно делится на 100.
3. Натуральные числа от 1 до 9 разбиты на три группы. Докажите, что произведение чисел в одной из групп не меньше 72.
Доказательство. Так как произведение всех данных чисел равно 9! = 362880, а 72³ = 373248. Из этого следует что произведение чисел одной из групп не меньше 72.
4. Докажите, что среди любых шести целых чисел найдутся два, разность которых кратна 5.
Доказательство. При делении целого числа на 5 возможны пять различных остатков: 0, 1, 2, 3 или 4. Так как чисел по условию 6, значит, по принципу Дирихле среди них обязательно найдутся два с одинаковыми остатками. Если мы рассмотрим их разность, то она будет давать при делении на 5 остаток 0, а значит будет делиться на 5.
5. В клетках таблицы 3 × 3 расставлены числа −1 , 0, 1. Докажите, что какие-то две из восьми сумм по всем строкам, всем столбцам и двум главным диагоналям будут равны.
Доказательство . Каждая из данных восьми сумм может принимать семь различных значений: от −3 до 3, значит, по принципу Дирихле какие-то две суммы совпадут.
6. Докажите, что из любых 7-ми натуральных чисел можно выбрать три числа, сумма которых делится на 3.
Доказательство. Так как имеется лишь три различных остатка от деления на 3 — 0, 1 и 2. Значит, по принципу Дирихле среди 7 натуральных чисел можно выбрать хотя бы 3 числа, остатки которых будут совпадать. Их сумма, делится на 3.
На основе задач данного параграфа мы можем сказать, что для решения задач этого типа необходимо знать основы теории чисел.
2.3 Решение геометрических задач
1. В квадрат со стороной 1 метр бросили 51 точку. Докажите, что какие-то три из них можно накрыть квадратом со стороной 20 см.
Доказательство.Разделим квадрат на 25 квадратов со стороной 20 см. По обобщенному принципу Дирихле, в какой-то из них попадёт, по крайней мере, три точки из тех, что бросили.
2. Внутри равностороннего треугольника со стороной 1 см расположено 5 точек. Докажите, что расстояние между некоторыми двумя из них меньше 0,5см.
3. В полотенце 4 м × 4 м моль прогрызла 15 дырок. Докажите, что из него можно вырезать коврик 1 м × 1 м, не имеющем внутри себя дырок.
Доказательство. Полотенце 4 м × 4 м разделим на 16 равных квадратов 1 м × 1 м. Из условия дырок только 15, по принципу Дирихле следует, что, хотя бы в одном квадрате не будет дырки.
4. Докажите, что если прямая k лежит в плоскости треугольника АВС и не проходит через каждую из его вершин, то она не может пересекать все три стороны треугольника.
Доказательство. Прямая k делит плоскость на две полуплоскости (рис.2). Три вершины треугольника АВС принадлежат двум полуплоскостям. Из этого следует, что по принципу Дирихле хотя бы две вершины лежат в одной полуплоскости относительно прямой k ипрямая не пересекает сторону, соединяющую эти вершины.
5. Дан равносторонний треугольник со стороной 2 см, внутрь него бросили 5 бобов. Докажите, что найдутся два боба, расстояние между которыми меньше 1 см.
Доказательство. Разделим треугольник на 4 равных треугольника как показано на рисунке (рис. 3). Стороны построенных треугольников будут равны 1 см. Из условия бросают 5 бобов, значит по принципу Дирихле в один из полученных треугольников попадет хотя бы 2 боба, расстояние между которыми будет меньше стороны треугольника, то есть меньше 1 см.
Для решения задач данного типа нужно выполнить дополнительные построения.
2.4 Решение комбинаторных задач
1. В коробке лежат шарики 4-х разных цветов (белые, черные, синие, красные). Какое наименьшее количество шариков надо вынуть из коробки, чтобы среди них оказались два шарика одного цвета?
Ответ: 5 шариков.
2. В бригаде 7 человек и их суммарный возраст – 332 года. Докажите, что из них можно выбрать трех человек, сумма возрастов которых не меньше 142 лет.
Доказательство. Выберем трёх старших членов бригады. Если им вместе 142 года, то хотя бы одному из них больше 47 лет. Если самому младшему из троих 47 лет, то им троим больше 142 лет. Пусть самому младшему из троих 47 лет или меньше, и им троим вместе менее 142 лет. Тогда на долю остальных 4-ых приходится более 332-142=190 лет, разделим 190 на 4-ых, получим 190 = 4 * 47 + 2. Тогда по принципу Дирихле одному из 4-ых больше 47 лет, это противоречит выбору троих самых старших в этой бригаде.
3. Докажите, что в любой момент турнира по шашкам (в котором каждый встречается с остальными участниками по одному разу) найдется два игрока, сыгравшие одинаковое число партий.
Доказательство. По принципу Дирихле, если в турнире k + 1 участник, то количество сыгранных партий у каждого спортсмена меняется от 0 до k. Но, если хотя бы у одного участника не сыграно ни одной партии, то ни у кого не может быть сыграно k партий (т. е. количество групп - k). Если хотя бы один сыграл все k партий, то ни у кого не может быть 0. Если k + 1 игрока распределять по k группам, то найдется группа, в которой не менее 2 игроков.
4. На контрольной работе 10 школьников решили в сумме 35 задач, причем среди них были решившие ровно одну, ровно две и ровно три задачи. Докажите, что кто-то из них решил не менее 5 задач.
Доказательство. Возьмем одного школьника, решившего ровно одну задачу, одного, решившего ровно две и одного, решившего ровно три. Эти трое решили в сумме 6 задач. Остается еще 7 школьников, решивших в сумме 29 задач. Значит, по обобщённому принципу Дирихле n = 7, k = 4, 7 * 4 + 1 = 29, из этого следует что найдётся кто-то из них, кто решил не менее 5 задач.
На примере данных задач, мы можем сказать, что их решение осуществляется путём выбора каких-либо предметов в нужном колличестве для получения ответа.
Рассмотрев типовые задачи по данной теме, нами были сформулирована последовательность действий для решения задач с применением принципа Дирихле:
Последовательность действий
Пример выполнения
Каждая грань куба раскрашена в чёрный или белый цвет. Докажите, что найдутся две одинаково раскрашенные грани, имеющие общее ребро.
Данная задача в преобразованиях не нуждается.
3. Выбрать для решения задачи удобную формулировку принципа Дирихле.
Для решения данной задачи выбираем следующую формулировку: «если в n клетках
Продолжение таблицы 1
4. Привести условия задачи к выбранной формулировке принципа Дирихле.
5. Получаем ответ или результат доказательства.
В ходе проделанной работы были изучены различные научные материалы по данной теме, разобраны и систематизированы типовые задачи: в арифметике, геометрии, теории чисел и комбинаторике. Разобраны разные формулировками данного принципа с их доказательством.
Была обобщена схема решения задач с применением принципа Дирихле и сформулирована последовательность действий для данного класса задач. Задачи были систематизированы и разобраны в соответствии с различным уровнем сложности.
Материал работы будет полезен для самостоятельного изучения при подготовке к математическим олимпиадам.
Список используемых источников
Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра: Учеб. для 9 кл. общеобразоват. учреждений – 16-е изд.– М.: Просвещение, 2011. – 287с.
Алфутова Н. Б, Устинов А. В. Алгебра и теория чисел. Сборник задач для математических школ. — 3-е изд., испр. доп. — М.: МЦНМО, 2009. — 336 с.
Бабинская И. Л. Задачи математических олимпиад. - М.: Наука, 1975. – 112 с.
БердичевскийВ. Л. Вариационные принципы механики сплошной среды. — М.: Наука, 2005. – 448 с.,
Болодурина И.П., Отрыванкина Т.М., Арапова О.С. и др. Дискретная математика. Часть 1: Учебное пособие — Оренбург: Оренбургский гос. ун-т, 2016. — 108с.
Венков Б.А. Элементарная теория чисел. – ОНТИ НКПТ СССР, 1937. – 222 с.
Виленкин Н.Я. Математика: Учеб. для 5 кл. общеобразоват. учреждений и –24-е изд., испр. – М.: Мнемозина, 2008. –280с.
Виленкин Н.Я., Виленкин А.Н., Сурвилло Г.С. и др. Алгебра: Учеб. для 8 кл. общеобразоват. учреждений и школьников с углубл. изучением математики - Под редакцией Н.Я. Виленкина. – 9-е изд., дораб. – М.: Просвещение, 2010. – 303с.
Виноградов И. М. Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — 2921 с.
Гильберт Рид К. С приложением обзора Германа Вейля математических трудов Гильберта. - М.: Наука, 1977. - 368 с.
Гусев В. А., Орлов А. И., Розенталь А. Л. И др. Внеклассная работа по математике в 6−8 классах: Пособие для учителя: Пер. со 2-го рус.изд. - Под ред. С. И. Шварцбурда. — Душанбе: Маориф, 1989. — 309с.
Дорогая И.Д. Метод Фурье, симметрии и функция Грина задачи Дирихле — Вестник Балтийского федерального университета им. И. Канта, 2009. — 6с.
Канель-Белов А. Я., Ковальджи А. К. Как решают нестандартные задачи - под ред. В. О. Бугаенко. — Изд. 6-е, стер. — М.: Изд-во МЦНМО, 2010. — 94 с.
Кастрица О.А., Мазаник С.А., Наумович А.Ф. и др. Математический анализ. Ряды и несобственные интегралы: учебное пособие — 392с.
Крепкогорский В.Л. Функциональный анализ: учебное пособие — Казань: КНИТУ, 2014. — 116с.
Мордкович А.Г., Семенов П.В. Алгебра и начала анализа: Учеб. для 11 кл. В 2 ч. Ч. 1. Учебник для общеобразоват. учреждений (проф. уровень) – М.: Мнемозина, 2007. – 287с.
Муштари Д. X. Подготовка к математическим олимпиадам: задачи, темы, методы. - Казанский ун-т, 1990. – 239 с.
Нигмедзянова А.М. Решение основных краевых задач одного многомерного вырождающегося эллиптического уравнения первого рода с отрицательным параметром методом — Известия ТулГУ. Естественные науки, 2013. — 10с.
Синкевич Г.И. – 200 - ЛЕТИЕ КАРЛА ВЕЙЕРШТРАССА. Математика в высшем образовании – 2015. №13 – 22 с.
Фарков А.В. Математические олимпиады: методика подготовки: 5-8 классы — Москва: ВАКО, 2012. — 176с.
Хаггарти Р. Дискретная математика для программистов — 2-е изд., исправленное. — Москва: Техносфера, 2012. — 400с.
Чулков П.В. Практические занятия по элементарной математике (2-й курс) — Учебное пособие. – М.: МПГУ, 2012. — 102с.
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Городская научно-практическая конференция школьников
секция Физико-математические дисциплины
тип работы Практико-ориентированный проект
Автор работы Иванников Даниил,
Руководитель Лобова Ольга Дмитриевна,
Курчатов, 2016 г.
Проект - учебный, практического применения. Проект направлен на развитие логического, творческого и нестандартного мышления учеников, воспитание их эстетического восприятия математики, развитие сообразительности и смекалки, что станет хорошим подспорьем в жизни ребят вне зависимости от того, какой жизненный путь они изберут. Приведены исторические сведения, формулировки принципа Дирихле и их доказательства. В работе показана теоретическая значимость принципа Дирихле как основного метода формирования теории чисел. Подтверждена практическая значимость неконструктивного доказательства, которое лежит в основе этого принципа . Задачи классифицированы по содержанию и по формулировкам.
II . Описание работы
1. Исторические сведения
3 тип. Обобщенный принцип Дирихле
2.Роль олимпиад с каждым годом становится все более значимой. И не случайно многие вузы стали проводить свои олимпиады для будущих абитуриентов, пресле дуя цель - привлечь школьников в данный вуз. Победители, занявшие призовые места, имеют преимущества при зачислении абитуриентов в вуз. Решая олимпиадные задания, я заметил, что для решения некоторой группы задач используется определённый способ, называемый принципом Дирихле, я решил изучить его подробнее.
Актуальность работы. Принцип Дирихле не рассматривается в учебниках математики, поэтому знакомство с новыми методами расширяет для обучающихся круг решаемых задач, учит мыслить, развивает сообразительность.
Гипотеза. Применение соответствующих формулировок принципа Дирихле – наиболее рациональный подход при решении задач олимпиадного уровня.
Объект исследования - принцип Дирихле
Предмет исследования - различные формулировки принципа Дирихле и их применение при решении задач.
Цель работы - изучить, один из основных методов математики, принцип Дирихле.
Задачи работы:
- изучить литературу по данной теме;
- научиться решать задачи на принцип Дирихле;
- выступить перед обучающимися 6-х классов для ознакомления их с данным принципом
Описание работы
Исторические сведения
Дирихле Петер Густав Лежен немецкий математик. Родился 13.02.1805г в вестфальском городе Дюрене в семье почтмейстера. В 12 лет Дирихле начал учиться в гимназии в Бонне, В 1829 году он перебирается в Берлин, где проработал непрерывно 26 лет, сначала как доцент, затем с 1831 года как экстраординарный, а с 1839 года как ординарный профессор Берлинского университета. В 1855 году Дирихле становится в качестве преемника Гаусса профессором высшей математики в Гёттингенском университете.
Петер Густав Лежён–Дирихле внёс существенный вклад в математический анализ, теорию функций и теорию чисел. Значительные работы Дирихле посвящены механике и математической физике.
Его научное наследие и его лекции значительно продвинули вперед развитие математических знаний в Германии.
5 мая 1859 года, он умер в Гёттингене от сердечного приступа, Мозг Дирихле хранится в отделе физиологии в Гёттингенском университете, наряду с мозгом Гаусса.
Теоретическая часть
Принцип Дирихле утверждает, что если множество из M элементов разбито на N непересекающихся частей, не имеющих общих элементов, где M > N, то по крайней мере в одной части будет более одного элемента.
Наиболее часто принцип Дирихле формулируется в одной из следующих форм:
Формулировка 1.
Если в n клетках сидит n +1 зайцев или больше зайцев, то найдётся клетка, в которой сидят по крайней мере два зайца .
Например. Если в 4(или n) клетках сидит 5 (или n+1) зайцев, то хотя бы в одной клетке находится более одного зайца (2 зайца).
Формулировка 2.
Предположим, m зайцев рассажены в n клетках. Тогда если m > n, то хотя бы в одной клетке содержится не менее m:n зайцев, а так же хотя бы в одной другой клетке содержится не более m:n зайцев.
Обобщенный принцип Дирихле : “Если в n клеток посадить kn+1 зайцев, то найдется хотя бы одна клетка, в которой находятся не менее чем k+1 заяц”.
( "Если в n клетках сидят не более nk-1 "зайцев", то в какой-то из клеток сидят не более k-1 "зайцев ".)
Докажем обобщенный принцип Дирихле . Доказательство от противного. Предположим, что не найдется такой клетки. Значит, в каждой клетке находится не более чем k зайцев. Тогда в n клетках не более чем kn зайцев. Но по условию у нас было kn+1 зайцев. Получилось противоречие, значит наше предположение неверно. Следовательно, найдется хотя бы одна клетка, в которой находятся не менее чем k+1 заяц.
Порядок применения принципа Дирихле
1 .Определить, что в задаче является "клетками", а что-"зайцами".
2.Применить соответствующую формулировку принципа Дирихле:
Если в n клетках сидят не более (n-1) "зайцев", то есть пустая "клетка".
Если в n клетках сидят (n+1) «зайцев", то есть клетка, в которой не менее 2-х "зайцев".
Если в n клетках сидят не более (nk-1) "зайцев", то в какой-то из клеток сидят не более (k-1) "зайцев".
Если в n клетках сидят не менее (nk+1) "зайцев", то в какой-то из клеток сидят не менее k+1 "зайцев".
Рассмотрим примеры задач, решаемых с помощью принципа Дирихле.
Задачи можно разбить на типы по постановке вопроса
Задача . В коробке лежат карандаши: 7 красных и 5 синих. В темноте берут карандаши. Сколько карандашей надо взять, чтобы среди них было не менее 2 красных и не менее 3 синих?
Задача 1. Дано 11 различных целых чисел. Докажите, что из них можно выбрать два числа, разность которых делится на 10.
Решение. При делении чисел на 10 могут получиться остатки: 0,1,2,3,4,5,6,7,8,9, всего 10, а чисел 11, значит по крайней мере, два числа из 11 дают одинаковый остаток при делении на10. Пусть это будут числа
А = 10а + с и В = 10 b + с. Тогда их разность делится на 10:
А - В =10 a + c -10 b - c =10 a -10 b = =10(а - b ). Так как один из множителей делится на 10, то и всё произведение разделится на 10.
3 тип. Обобщенный принцип Дирихле
Задача . На олимпиаде 10 школьников решили в сумме 35 задач, причем среди них были решившие ровно 1 задачу, ровно 2 задачи и ровно 3. Доказать, что кто-то из них решил не менее пяти задач.
Геометрическая задача
Задача. Внутри равностороннего треугольника со стороной 1 расположено 5 точек. Доказать, что расстояние между некоторыми двумя из них меньше 0,5.
Решение.
Средние линии правильного треугольника со стороной 1 разбивают его на четыре правильных треугольничка со стороной 0,5. Назовём их "клетками", а точки будем считать "зайцами". По принципу Дирихле из пяти точек хотя бы две окажутся в одном из четырёх треугольничков. Расстояние между этими точками меньше 0,5, поскольку точки не лежат в вершинах треугольничков.
Задание 20. ЕГЭ 2016 (базовый уровень). В корзине лежат 30 грибов – рыжиков и груздей. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов – хотя бы один груздь. Сколько рыжиков и сколько груздей в корзине?
Решение
Так как среди любых 12 грибов хотя бы один – рыжик, то груздей не больше 11. Так как среди любых 20 грибов хотя бы один – груздь, то рыжиков не больше 19. А так как всего в корзине 30 грибов, то груздей ровно 11, а рыжиков ровно
Изучив литературу по теме принцип Дирихле, проанализировав виды и типы задач, которые решаются с использованием данного принципа, я сделал следующие выводы:
- Принцип Дирихле важен и полезен, этот принцип является мощным логическим методом, с помощью которого решаются не только арифметические задачи, но и задачи с геометрическим содержанием, комбинаторные задачи. Его можно применять в повседневной жизни, что развивает логическое мышление.
- Многие олимпиадные задачи решаются на основе этого специального метода, поэтому его целесообразно изучать самостоятельно или во внеурочной деятельности.
- Моё выступление перед одноклассниками показало, что данный метод решения задач понятен и интересен обучающимся 6-х классов.
Я считаю, что проделанная мною работа, дала положительные результаты. Элементы моей работы можно использовать для ознакомления с принципом Дирихле среди одноклассников, при подготовке к олимпиадам, на занятиях математического кружка, к подготовке к экзаменам. В процессе исследовательской деятельности мною были подобраны задачи, решаемые с помощью принципа Дирихле.
По итогам проекта мною составлен сборник задач для самостоятельной работы всех тех, кто заинтересовался этим методом решения задач.
Для тех, кто заинтересовался данной темой рекомендую литературу и Интернет-ресурсы, которые вы видите на слайде.
1.Андреев А.А., Горелов Г.Н., Люлев А.И., Савин А.И. "Принцип Дирихле", Самара "Пифагор", 1997.
2.Д. X. Муштари. Подготовка к математическим олимпиадам: задачи, темы, методы. Казанский ун-т, 1990.
В математике существует множество принципов. Некоторые из них достаточно просты и понятны даже новичку, а некоторые требуют определенных объяснений и доказательств. Однако все они весьма эффективны, и их легко можно применять на практике. Одним из них является принцип Дирихле (известный также как принцип голубей/кроликов). Это достаточно простое утверждение, способное помочь в решении многих математических задач.

История
Современная формулировка и доказательство
На сегодняшний день существует несколько разных формулировок данного принципа. Самая понятная и простая подразумевает, что нельзя посадить 8 кроликов в 3 клетки так, чтобы в каждой было не больше 2. Более научная и сложная формулировка, объясняющая принцип Дирихле, гласит: если в k ячеек находится k+1 зайцев, то, по крайней мере, в 1 ячейке будет располагаться больше одного зайца. А если в k ячеек находится k-1 зайцев, то по крайней мере в 1 ячейке будет располагаться меньше одного зайца. Доказательство этого утверждения совсем простое, так сказать, от противного. Если предположить, что в каждой ячейке располагается зайцев меньше, чем k-1/k, тогда в k ячеек зайцев меньше чем k*k-1/k = k-1, а это противоречит первоначальным условиям.
В действительности такой простой и понятный принцип значительно облегчает решение задач по математике и доказательства многих трудоемких теорем. Просто необходимо учитывать, что зайцев и ячейки можно легко заменить на математические предметы и объекты (цифры, точки, отрезки, фигуры и т. д.).
Еще одна формулировка
Иногда задачи на принцип Дирихле - не такие простые и очевидные, как с животными в ящиках. Необходимо переносить этот принцип на математические множества, чтобы отыскать какие-либо решения. В таком случае можно опираться на другую, более сложную формулировку.
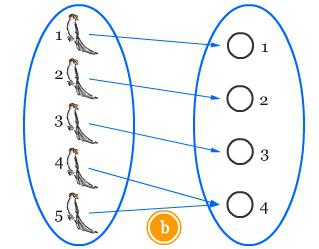
Если отобразить множество S, содержащее d+1 элементов, в множество R с совокупностью d элементов, то два элемента из множества S будут иметь одинаковый образ.
Хотя современные ФГОС по математике предъявляют к ученикам творческие требования и предлагают нестандартные варианты, решение через утверждение Дирихле не всегда такое простое и понятное. Иногда очень трудно определить, какую величину считать животным, а какую – клеткой, и каким образом факт наличия двух животных в одной клетке поможет решению задачи. Да и если удастся в этом разобраться, все равно нельзя определить, в какой именно клетке будет находиться объект. То есть можно просто доказать существование такой ячейки, но нельзя конкретизировать ее.
Пример № 1. Геометрия
Современные примеры решения задач демонстрируют, что животными и клетками могут выступать совершенное различные математические предметы.
Прямая k проходит через плоскость треугольника ABC, однако не пересекает ни одну его вершину. Необходимо доказать, что она не может пересекать три его стороны.
Представим, как прямая k разбивает треугольник на две плоскости, назовем их s1 и s2. Будем считать, что s1 и s2 открытые, то есть не содержащие прямую k. Ну а сейчас - самое время применить принцип Дирихле. Задачи с решениями могут продемонстрировать, что под кроликами и ячейками в современных условиях подразумеваются разнообразные объекты. Так, вместо зайцев мы подставим вершины треугольника, а вместо ячеек – полуплоскости. Поскольку проведенная прямая k не пересекает ни одну из вершин, то каждая из них находится в той или иной плоскости. Но поскольку вершины в треугольнике три, а плоскости у нас всего две (s1 и s2), то одна из них будет содержать две вершины. Предположим, что это вершины A и B, и находятся они в полуплоскости s2 (то есть лежат по одну сторону от k). В таком случае отрезок АВ не пересекает прямую k. То есть в треугольнике есть сторона, которую прямая k не пересекает.
Альтернативное решение
В данной задаче мы предположили, что в одной плоскости находятся точки А и В, однако принцип Дирихле не указывает конкретную ячейку, поэтому точно так же мы могли указать, что в одной плоскости разместились вершины С и В, или А и С. Для данной задачи совсем не важно, какую сторону треугольника не пересекает прямая k. Поэтому указанный принцип идеально подходит для ее решения.
Пример № 2. Геометрия
В середине равностороннего треугольника АВС (у которого АВ = ВС = АС = 1) разместилось 5 точек. Необходимо доказать, что две из них располагаются на расстоянии меньше 0,5.
Если провести в правильном треугольнике АВС средние линии, они разделят его на 4 маленьких правильных треугольника со сторонами ½ = 0,5. Предположим, что эти треугольники – ячейки, а точки внутри них – кролики. Получается, у нас есть 5 кроликов и 4 ячейки, следовательно, в одной из них будет находиться как минимум два кролика. Учитывая то, что точки не являются вершинами (так как они располагаются внутри треугольника АВС, а не на одной из его сторон), они будут размещаться внутри маленьких фигур. Следовательно, расстояние между ними будет меньше, чем 0,5 (поскольку величина отрезка внутри треугольника никогда не превышает величины его самой большой стороны).
Пример № 3. Комбинаторика
В других областях также можно удачно применять принцип Дирихле: комбинаторика и математическая физика уже давно опираются на него при решении задач.
Допустим, вокруг округлённого стола стоят на равном расстоянии друг от друга m флажков разных стран, а за столом сидят m представителей от каждой страны, причем каждый из них расположился рядом с чужим флажком. Нужно доказать, что при определенном вращении стола хотя бы двое из представителей окажутся возле своих флажков.
Получается, что существует m-1 способов развернуть стол так, чтобы изменилось взаиморасположение представителей и флажков (если исключить начальное размещение стола), но при этом остается m представителей.
Приступая к решению такой задачи, важно понимать, что начальное положение – это тоже ячейка, но по условию задачи она заведомо пустует, поэтому мы уменьшаем общее количество на 1 (m-1).
Пример № 4. Теория чисел
Принцип Дирихле в теории чисел также имеет огромное значение.
Предположим, на листике тетради в клетку ученик произвольно в узлах клеточек проставил 5 точек. Необходимо доказать, что как минимум один отрезок с вершинами в этих точках пройдет через узел клеточки.
Для начала нужно изобразить на листе тетради систему координат, основа которой расположится в одном из узлов. Оси системы координат будут совпадать с линиями сетки, а за единичный отрезок принята сторона клеточки. Получается, что все 5 отмеченных точек будут находиться в системе, а их координаты будут только целым числом (четным или нечетным). Таким образом, мы получим 4 варианта координат: (четный; четный), (нечетный; четный), (четный; нечетный) и (нечетный; нечетный). А значит, 2 из 5 точек будут соответствовать одному варианту. Если посмотреть на ситуацию с позиции Дирихле, то необходимо обозначить точки как зайцев, а варианты координат - как ячейки. Мы получаем 5 зайцев и 4 клетки, соответственно, в одной из них будет минимум 2 животных. Допустим, это точки Р и А, с координатами (x4, y3) и (x5, y6). Середина отрезка, соединяющего эти две вершины, будет иметь координаты ((x4+x5) / 2), ((y3+y6) / 2)), которые будут целыми числами в условиях соответствующей четности x4 и x5, y3 и y6. Получается, что середина отрезка расположилась в узле клетки.
Пример № 5
Достаточно много задач разной сложности можно решить через принцип Дирихле. Задачи с решениями разнообразных математических и логических вопросов достаточно часто опираются на этот принцип.
На прямой дороге вырыты маленькие поперечные канавки. Расстояние между всеми канавками одинаковое и равно оно Ö2 м. Необходимо доказать, что, независимо от ширины канавок, человек, шагающий по дороге с интервалом 1 м, однажды попадет ногой в одну из них.
Обобщение принципа
Материалы по математике, кроме стандартных (простых и не очень) формулировок, содержат также одну обобщенную, которая используется для выявления более двух объектов, похожих друг на друга. Она утверждает, что если dm + 1 кроликов поместить в d ячеек, то как минимум m + 1 кролик окажется в одной ячейке.
Пример № 6. Обобщение
Прямоугольник с площадью 5 х 6 клеток (30 клеток), закрашенных только 19. Можно ли обнаружить квадрат площадью 2 х 2 клетки, в котором минимум три будут закрашены?
Нашу фигуру необходимо разделить на 6 блоков по 5 клеток. Исходя из утверждения Дирихле, в одной из них будет закрашено не менее 4 клеточек (19/6 = 4). Тогда в одном из квадратов площадью 4 клеточки, расположенном в одном из блоков, будет закрашено минимум 3 клетки.
Пример № 7
Класс, в котором 25 человек. Из любых случайно выбранных 3 учеников двое будут друзьями. Необходимо доказать, что в классе находится школьник, у которого больше 11 приятелей.
Два решения вопроса

Для начала возьмем двух школьников, которые не дружат с друг другом (поскольку если бы все они дружили между собой, то в каждой тройке было бы три друга и каждый ученик дружил бы с 24 другими). Оставшиеся 23 одноклассника будут дружить с одним из нашей двойки, поскольку в противном случае нашлась бы тройка, где нет друзей (а это противоречит изначальному условию задачи). Получается, что один из двух школьников будет дружить как минимум с 12 учениками. В данном случае ученики – это кролики, а условия "друзья они или нет" – это ячейки. Мы имеем 23 животных и только 2 клетки. Соответственно, в одной из них как минимум 23/2 = 11,5, т. е. 12 кроликов. То есть один из 2 выбранных нами учеников будет дружить как минимум с 12 своими одноклассниками (или даже больше). Конечно же, существуют и другие методы решения задачи, однако данный - один из самых понятных и удобных.
Читайте также:

