Сообщение на тему площадь трапеции

Обновлено: 05.07.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Выберите документ из архива для просмотра:

Приложение 1_буклет Трапеция.pub

Выбранный для просмотра документ ЗАЯВКА.docx

на участие в муниципальной Конференции

taimyr 4.1@ mail . ru , yaporova @ yandex . ru

Информация об участнике

Низовцев Руслан Алексеевич

Домашний адрес, телефон

г.п. Диксон ул. Водопьянова д.24, кв.36

Информация о работе

9 способов нахождения площади трапеции

Информация о научном работнике или педагоге наставнике

Низовцева Джамиля Ахмедулловна

Место работы, должность

Ученая степень (если имеется)

Выбранный для просмотра документ НПК Низовцев Руслан.doc

Администрация Таймырского Долгано-Ненецкого муниципального района

Управление образования

Таймырское муниципальное казенное общеобразовательное учреждение

Муниципальная Конференция

Исследовательская работа

Работу выполнил :

Низовцев Руслан Алексеевич,

г.п. Диксон, ул. Водопьянова д.24 кв.36

Научный руководитель :

Низовцева Джамиля Ахмедулловна

2015-2016 уч. год

Автор: Низовцев Руслан Алексеевич

Цель научной работы: определить, существуют ли другие способы нахождения площади трапеции

Основные результаты научного исследования:

существует много способов нахождения площади трапеции;

при решении задач используется тот метод, который удобен.

Значение геометрии в нашей жизни

Способы нахождения площади трапеции

В ходе работы нам предстояло подтвердить или опровергнуть суждение о том, что существуют другие способы нахождения площади трапеции, помимо описанного способа в учебнике.

Объект исследования: трапеция

Предмет исследования: площадь трапеции

Цель исследования: определить, существуют ли другие способы нахождения площади трапеции.

Задачи исследования:

Проанализировать литературу по данному вопросу;

Изучить вопрос по нахождению площади трапеции в учебнике геометрии 7-9 класс А.В. Погорелов.

Провести анализ тестов ОГЭ с 2011 г по 2016г по математике и определить частоту появления задач на нахождение площади трапеции в КИМах.

Методы исследования:

поисковый метод с использованием научной и учебной литературы, интернета;

исследовательский метод определяется как самостоятельное решение проблемы с применением рассуждения, доказательства и анализ фактов.

практический метод при определении частоты появления задач на нахождение площади трапеции, составлении буклета, проведение видео опроса

Практическая значимость работы определяется возможностью использования данного материала при решении геометрических задач, при доказательстве некоторых положений.

Совместно с руководителем был разработан ход исследования:

Изучить теоретический материал учебника и дополнительных источников информации и найти новые способы нахождения площади трапеции.

Провести анализ тестов ОГЭ и определить частоту появления задач на нахождение площади трапеции.

Оформить результаты, сделать соответствующие выводы.

2. Значение геометрии в нашей жизни 1,2

Геометрия зародилась в глубокой древности. Строя жилища и храмы, украшая их орнаментами, размечая землю, измеряя расстояния и площади, человек применял свои знания о форме, размерах и взаимном расположении предметов, он использовал свои геометрические знания, полученные из наблюдений и опытов.

Среди множества различных геометрических фигур на плоскости выделяется большое семейство четырёхугольников. В обычной жизни на каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает каждый. Каждый понимает смысл слов: площадь комнаты, площадь садового участка. Подумайте и самостоятельно ответьте на вопрос: что такое “площадь”? И вы увидите, что не так-то это просто. Даже математики смогли создать соответствующую математическую теорию сравнительно недавно. Правда, это никому не мешало успешно использовать понятие площади и в науке, и на практике с незапамятных времен. Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Согласно легенде, эта наука возникла в Древнем Египте, где после каждого разлива Нила приходилось заново производить разметку участков, покрытых плодоносным илом, и вычисление их площадей.

По-видимому, в древности приходилось рассматривать лишь участки, мало отличающиеся от прямоугольника по форме, а для таких участков погрешность невелика. Лишь в последствие было полностью развито учение о площадях и получены точные формулы для вычисления площади прямоугольника, параллелограмма, треугольника, трапеции и других многоугольников.

Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников.

3. Способы нахождения площади трапеции

Одним из многоугольников является трапеция.

Трапеция, у которой боковые стороны равны, называется равнобокой, равнобочной или равнобедренной трапецией.

Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

Трапецию можно встретить как в повседневной жизни - быту, так и в архитектуре и природе. Значение трапеции в нашей жизни я оформил в виде буклета. Приложение 1.

Дано: ABCD - трапеция

Найти площадь S _ABCD

Провели диагональ BD . Тогда наша трапеция разбивается на две части: два треугольника Δ ABD и Δ BCD .

ДН= ВЕ – как высоты трапеции (расстояние между параллельными прямыми АВ и СД)

Вывод: площадь трапеции равна произведению полусуммы оснований на высоту трапеции.

Провели высоты АН и D К , A Н = D К, AD = HK . Тогда наша трапеция разбивается на три части: треугольник А H В, прямоугольник A Н D К и треугольник CKD .

3. S _ABCD = A = AH

Вывод: площадь трапеции равна произведению полу суммы оснований на высоту трапеции.

Решение:

Провели СК ‖ АВ, высоту ВН. Тогда наша трапеция разбивается на две части: параллелограмм АВСК (по определению, так как АВ ‖ СК по построению, АК ‖ ВС по условию) и ΔКС D . Причём, высоты параллелограмма и треугольника равны.

2. Таким образом, S _ABCD = S _ABCK + S _KCD

Вывод: площадь трапеции равна произведению полу суммы оснований на высоту трапеции.

Через середину стороны CD (точка К) провели прямую, пересекающую сторону AD в точке L .

Рассмотрим треугольники BCK и LD К: CK = DK (по построению), ∟В C К = ∟ LDK (как внутренние накрест лежащие при параллельных прямых ВС и LD и секущей CD ), ∟ CKB = ∟ DKL (как вертикальные), Δ BCK = Δ LD К (по стороне и двум прилежащим к ней углам), следовательно, BC = LD и S _BCK = S _LD _К .

Вывод: площадь трапеции равна произведению полу суммы оснований на высоту трапеции.

Через середины сторон AB и CD (точки M и K ) провели перпендикуляры NH и PT к основаниям трапеции.

Рассмотрим Δ AMH и Δ BMN : ∟ H = ∟ N = 90 0 , AM = MB (по условию), ∟ AMH = ∟ BMN (как вертикальные), значит, ΔAMH = ΔBMN (по гипотенузе и острому углу), следовательно, AH = BN и S _AMH = S _BMN

Рассмотрим Δ CPK и Δ DTK : ∟ T = ∟ P = 90 0 , CK = KD (по условию), ∟ CKP = ∟ DKT (как вертикальные), значит, ΔCPK = ΔDTK (по гипотенузе и острому углу), следовательно, CP = DT и S _CPK = S _DTK

Вывод: нахождение площади трапеции сводится к нахождению площади прямоугольника.

Провели высоты ВН и СК, ВН = СК, HK = BC . Тогда наша трапеция разбивается на три части: треугольник АВН, прямоугольник НВС K и треугольник CKD .

Вывод: площадь трапеции равна произведению полу суммы оснований на высоту трапеции.

Решение:

В трапеции даны диагонали AC = d ₁ , BD = d ₂ , ∟ COD = .

∟ AOB = ∟ COD (как вертикальные), ∟ BOC = ∟ AOD = 180 0 – (по свойству смежных углов), и = .

Вывод: площадь трапеции равна произведению диагоналей трапеции на синус угла между ними деленному на 2.

В трапеции ABCD MN – средняя линия, т. е. AM = MB и CN = ND, MN = .

Вывод: площадь трапеции равна произведению средней линии на высоту трапеции

Решение.

Через середину стороны CD трапеции ABCD провели перпендикуляр KM к стороне AB , т. е. CK = KD , KM = q , AB = d .

ΔCPK = ΔDNK по стороне и двум прилежащим к ней углам (∟ CKP = =∟ DKN (как вертикальные, CK = DK (по условию), ∟ PCK = ∟ NDK (как накрест лежащие при параллельных прямых), значит, S _CPK = S _DNK

Вывод: при данных условиях нахождение площади трапеции сводится к нахождению площади параллелограмма.

При исследовании способов решения задачи, мы увидели, что площадь трапеции может быть найдена:

С помощью площади прямоугольника;

Через площадь треугольника (наиболее часто);

С помощью площади параллелограмма;

Через среднюю линию трапеции;

Через диагонали трапеции и угол между ними.

Таким образом, существует много способов нахождения площади трапеции. При решении задач используется тот метод, который удобен.

Исследование 10

Цель: определить, как часто встречаются задачи на нахождение площади трапеции в тестах ОГЭ по математике

Ход исследования:

Рассмотреть учебные пособия по подготовке к ОГЭ по математике с 2011г по 2016г. 1,10, 11,12,13,14,15

Подсчитать количество тестов по годам

Подсчитать, количество тестов, где встречаются задания на нахождение площади трапеции.

Цель: Показать многообразие подходов при решении одной геометрической задачи и найти более рациональный способ решения задачи.

Задачи:

Подобрать и решить геометрическую задачу несколькими способами, применив основной материал курса 8 класса.
Провести анализ подходов при решении одной геометрической задачи.

Актуальность данной работы определяется тем, что знания и умения находить площадь трапеции имеют огромное значение для решения задач, в том числе и заданий единого государственного экзамена. Данное исследование, поможет найти новые подходы к решению геометрических задач.

Вложение	Размер
ploshchad_trapetsii_9_klass.docx	776.08 КБ

Предварительный просмотр:

Глава 1.Полезные свойства трапеции

Глава 2. Нахождение площади трапеции

Глава 3 Применение для решения задач

Список использованной литературы

«Наглядность, воображение принадлежат больше искусству,

Среди множества различных геометрических фигур на плоскости выделяется большое семейство четырёхугольников. В обычной жизни на каждом шагу мы встречаемся с понятием “площадь”. Что такое “площадь”, знает каждый. Измерение площадей считают одним из самых древних разделов геометрии; в частности название “геометрия” (т.е. “землемерие”) связывают именно с измерением площадей. Определение площадей геометрических фигур – одна из древнейших практических задач. Правильный подход к их решению был найден не сразу, но уже древние греки умели правильно находить площади многоугольников. На уроке геометрии мы доказывали теорему о нахождении площади трапеции.

Гипотеза . Эффективность выбранного пути решения геометрической задачи зависит от постановки задачи.

Подобрать и решить геометрическую задачу несколькими способами, применив основной материал курса 8 класса.
Провести анализ подходов при решении одной геометрической задачи.

Объект исследования: трапеция

Предмет исследования : площадь трапеции.

Исследовательский метод определяется как самостоятельное решение проблемы с применением рассуждения, доказательства и анализ фактов.

Совместно с руководителем был разработан ход исследования:

1. Изучить теоретический материал учебника и дополнительных источников информации и найти новые способы нахождения площади трапеции.

2. Оформить результаты, сделать соответствующие выводы.

В ходе работы нам предстояло подтвердить или опровергнуть суждение о том, что существуют другие способы нахождения площади трапеции

Глава 1.Полезные свойства трапеции.

Слово трапеция используется в геометрии для обозначения четырехугольника, характеризующегося определенными свойствами. Кроме того, оно имеет еще несколько значений. В архитектуре используется для обозначения симметричных дверей, окон и зданий, построенных широкими у основания и сужающимися к верху (в египетском стиле). В спорте — это гимнастический снаряд, в моде — платье, пальто или другой вид одежды определенного кроя и фасона.

В евклидовой геометрии так называют выпуклый четырехугольник, имеющий одна пару противоположных сторон, которые обязательно параллельны друг другу. Следует вспомнить несколько определений для того, чтобы найти площадь трапеции. Параллельные стороны этого многоугольника называются основаниями, а две других — боковыми. Высотой трапеции является расстояние между основаниями. Средней линией принято считать линию, соединяющую середины сторон боковых. Все эти понятия (основания, высота, средняя линия и боковые стороны) являются элементами многоугольника, являющегося частным случаем четырехугольника.

S = ½ ( a + b)· h.
S = ½· m, где m – средняя линия.
S = ½· · ·

Где p – полупериметр.

Свойство отрезка, соединяющего середины диагоналей трапеции .

Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

Свойство высоты равнобедренной трапеции, проведенной из

вершины тупого угла :

Высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.

Свойством треугольников, на которые разбивается трапеция ее

Диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики.

С в ойство отрезка, проходящего через точку пересечения диагоналей

трапеции параллельно основаниям .

Отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.

В трапеции точка пересечения диагоналей, точка пересечения продолжения боковых сторон, середины оснований трапеции лежат на одной линии.

Свойство длины отрезка разбивающего трапецию на две подобных.

Отрезок, разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований .

Свойство отрезка, делящего трапецию на две равновеликие .

Длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований.

Трапеция может быть вписана в окружность в том и только в том случае, когда она равнобедренная.

Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.

Полезные следствия того, что в трапецию вписана окружность:

1. Высота описанной трапеции равна двум радиусам вписанной окружности.

2. Боковая сторона описанной трапеции видна из центра вписанной окружности под прямым углом.

Следствия для равнобедренной описанной трапеции :

Высота равнобедренной описанной трапеции есть среднее геометрическое оснований трапеции
h = 2r = √(ab).

Рассмотренные свойства позволят более глубоко познать трапецию и обеспечат успешность в решении задач на применение ее свойств.

Глава 2. Нахождение площади трапеции

Задача. Найти площадь трапеции, основания которой равны 40 см и 20см, а боковые стороны 12 см и 16 см.

I подход к решению задачи

Задача сводится к нахождению высоты H.

Проведем отрезки ВМ и СN так, что ВМ┴АD и СN┴АD, тогда ВСNМ – прямоугольник. Поэтому ВМ = СN и ВС = МN.

Но в таком случае АМ + ND =20

Пусть АМ = х (см), тогда ND = 20 – х (см).

По теореме Пифагора из ▲АВМ и ▲СND: Н² = 12² - х² и Н² =16² - (20 – х) ².

Составим равенство 12² - х² = 16² - (20 – х) ², 144 - х² = 256 – 400 + 40х - х² , 40х = 288,

х = 7,2 (см ).Находим высоту Н: Н² = 12² – 7,2² = 144 – 51,84 = 92,16,

Находим высоту Н: Н = (см).

Тогда S ABCD = (см²)Ответ: 288 (см²)

II подход к решению задачи

Пусть ВN ┴АD и ВК‌‌║СD, тогда ВСDК – параллелограмм.

Значит ВК = СD = 16 (см), КD = ВС = 20 (см). Пусть ВN ┴ АD и ВК‌‌ ║ СD, тогда ВСDК – параллелограмм.

Значит ВК = СD = 16 (см), КD = ВС = 20 (см).

Пусть АN = х (см), тогда NК = (20 –х) см.

Выразим высоту Н из треугольников АВN и ВNК по теореме Пифагора:

Н² = 12² - х² и Н² =16² - (20 – х) ².

Составим равенство 12² - х² = 16² - (20 – х) ², 144 - х² = 256 – 400 + 40х - х² , 40х = 288, х = 7,2 (см ). Н = 9,6см.

Значит площадь трапеции

S ABCD = (см²). Ответ: 288 см²

III подход к решению задачи

Применим к нему одно из следствий теоремы Пифагора, в котором говорится о том, что квадрат катета равен длине проекции этого катета на гипотенузу, умноженной на длину гипотенузы . Пусть ВN ┴АД и ВК‌‌║СД, тогда КВСД – параллелограмм и

ВК = СД = 8 (см), КД = ВС = 10 (см).

Рассмотрим треугольник АВК: АВ = 12 см, ВК= 16 см, АК = 20 см. Так как 20² = 12² + 16², то треугольник АВК – прямоугольный. Применим к нему одно из следствий теоремы Пифагора, в котором говорится о том, что квадрат катета равен длине проекции этого катета на гипотенузу, умноженной на длину гипотенузы. Для нашего случая: 12² = х ∙20, откуда х = 7,2 (см). Применим терему Пифагора к треугольнику АВN, вычислим Н: Н = 9,6см.Значит площадь трапеции

S ABCD = (см²). Ответ: 288 см²

IV подход к решению задачи

Треугольник АВК – прямоугольный (угол АВК = 90° по теореме, обратной теореме Пифагора, так как 20² = 12² + 16²).Площадь треугольника АВК вычисляется как полупроизведение его катетов, т.е.

V подход к решению задачи

По теореме, обратной теореме Пифагора, треугольник АВК – прямоугольный. Тогда Sinα= . Но треугольник АВN – тоже прямоугольный (по построению ВN ┴АК). Тогда ВN=АВ∙ Sinα = 6∙ . Аналогичные выкладки можно проделать и для угла .Дальнейшее решение очевидно.

VI подход к решению задачи

В треугольнике АВК известны три стороны, поэтому для нахождения площади можно применить формулу Герона. Для этого сначала подсчитаем полупериметр треугольника АВК. По определению р=0,5(12+16+20)=24смТеперь найдем площадь треугольника АВК:

Но площадь этого треугольника можно вычислить и по формуле S =20h|2, отсюда h = 9,6см

VII подход к решению задачи

Проведем ВК║СД и установим, что ВС=КД, тогда АК=20. По теореме, обратной теореме Пифагора, устанавливаю, что угол АВК=90°, но тогда и угол при вершине М равен 90° по теореме об углах, образованных двумя параллельными прямыми и секущей.

Треугольники АВК и АМД – подобны (по двум равным углам: угол А – общий, угол В равен углу М), коэффициент подобия k = 2, так как k= . Отсюда АМ=АВ∙ k = 24 см, ДМ = ВК∙ k = 32 см. Но тогда ВМ = 12см, МС = 16 см, так как В – середина отрезка АМ, С – середина МД. Поскольку треугольники АМД и ВМС прямоугольные, Sвмс=0,5(BM*MC) S AND =0,5*(АМ*DM) Теперь легко найти площадь трапеции,как разность площадей 288

В этом решении была использована лишь часть того, что можно было извлечь из подобия треугольников (т.е. лишь зависимость между сторонами подобных треугольников). Но можно изменить последний фрагмент решения и воспользоваться тем фактом, что отношение площадей подобных треугольников равно k², т.е. .Тогда .

Глава 3 Применение для решения задач. Задачи практической направленности

Может возникнуть вопрос, а что если трапеция будет иметь другие размеры?

Рассмотрим следующие случаи:

1. Основания трапеции равны 10 и 20см , боковые стороны 6 и 8см. Этот случай может быть также использован для всех способов решения.

2. Основания трапеции равны 6 и 10см, боковые стороны 8 и 20см.

Треугольник АВС со сторонами 8, 20 и 4 см не существует, т.к 20>8+4 Значит, задача решения не имеет.

3. Основания трапеции равны 8 и 10см, боковые стороны 6 и 20см.

Треугольник АВС со сторонами 2, 6 и 20 см не существует, т.к. 20>6+2 Значит, задача решения не имеет.

4. Основания трапеции равны 6 и 8см, боковые стороны 10 и 20см.

Треугольник АВС со с торонами 10, 2 и 20 см не существует, т.к.20>10+2 Значит задача решения не имеет.

Основания трапеции равны 6 и 20см, боковые стороны 8 и 10см.

Для решения задачи

один из подходов,

Основания трапеции равны 8 и 20см, боковые стороны 6 и 10см.

Для решения задачи

один из подходов,

При решении задачи в 5 и 6 случаях, вычисления получаются уже сложными и громоздкими.

Задачи практической направленности

Бухгалтер строительной фирмы

Строительная фирма заказывает заводу металлоконструкций 25 окон, образец которых вы видите на фото. Размеры стекол вы видите на рисунке. Стоимость 1м 2 стекла 120 руб. Рассчитайте стоимость стекол, необходимых для изготовления этих окон.

Задача исторического характера

В Старинных русских рукописях содержатся способы измерения площадей различных фигур. Там утверждалось:

что фигуры с равными периметрами замыкают равные площади;(проверьте справедливость этого утверждения на примере квадрата и ромба, имеющих равные стороны)
площадь треугольника измеряли как половину от произведения меньшей стороны на большую;
площадь трапеции принималась равной произведению полусуммы оснований на длину меньшей боковой стороны (площадь, найденная таким способом больше или меньше настоящей?) .

Найдите в этих утверждениях ошибки.

Налог на землю составляет 1% от стоимости земли. Найдите стоимость предложенного участка земли, если 1 м 2 стоит 20 тыс. рублей. Рассчитайте налог на этот участок земли.

Учащиеся школы поздравили весь педагогический коллектив школы с праздником, заказав поздравление в газете. Найдите стоимость объявления, если стоимость 1см 2 объявления 4рубля.

Для решения данной задачи надо было вспомнить:

определение трапеции и формулу нахождения ее площади;
свойства прямоугольника и параллелограмма;
теорему Пифагора;
пропорциональность отрезков в прямоугольном треугольнике;
теорему, обратную теореме Пифагора;
площадь прямоугольного треугольника;
площадь треугольника через основание и высоту;
формулу Герона для вычисления площади треугольника;
подобие треугольников;
теорему об отношении площадей подобных треугольников;
тригонометрические зависимости в треугольнике

После анализа всех подходов к решению задачи, я для себя отметила, что лучшими из них оказались первое и последнее. Первое решение выигрывает потому, что кажется наиболее естественным, а последнее выглядит наиболее простым и оригинальным благодаря дополнительным построениям, в результате которых трапеция была разбита на три равных треугольника. Следовательно, мы пришли к выводу, что существует много способов нахождения площади трапеции. При решении задач используется тот метод, который удобен.

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Но в классической программе учителя дают далеко не все формулы, с помощью которых можно вычислить нужное значение. И ограничиваются, как правило, одной или двумя.

Мы же дадим максимально развернутый ответ на этот вопрос. Ведь трапеция – это весьма примечательная и сложная фигура в геометрии. А соответственно, и формулы для вычисления ее площади отличаются определенной сложностью и громоздкостью.

Что такое трапеция

Но для начала будет нелишним напомнить, что из себя представляет трапеция.

Трапеция – это геометрическая фигура, которая является четырехугольником, и у которой две противоположные стороны параллельны.

Последнее утверждение очень важное. ТОЛЬКО ДВЕ противоположные стороны параллельны у трапеции. Ведь если бы обе пары лежали на параллельных прямых, то это был бы уже параллелограмм.

Вот так выглядит трапеция:

А вот так параллелограмм:

Кстати, именно по этому принципу древний математик Евклид и разделил все четырехугольники на две большие категории.

Что такое площадь

Раз уж мы решили вычислять эту величину, напомним, что она обозначает.

Площадь – это численное значение геометрической фигуры, нарисованной в двухмерном (плоском) пространстве. А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.

В нашем случае площадь трапеции – это область, закрашенная синим цветом:

Главная формула для вычисления площади трапеции

Та формула, которую изучают в школе, основана на вычислении площади трапеции по длине ее оснований и высоте.

Основания трапеции – это стороны, которые лежат на параллельных прямых. Другая пара сторон называется боковыми.

Высота – это отрезок, проведенный из вершины любого угла к противоположному основанию под углом 90 градусов.

То есть мы имеем вот такие исходные данные:

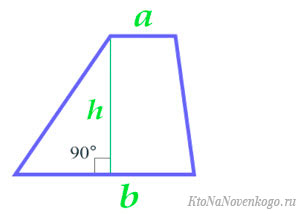
И тогда формула для вычисления площади трапеции выглядит вот так:

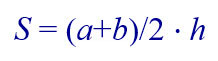
Например, если длины сторон и высота равны:

то площадь такой трапеции будет равна:

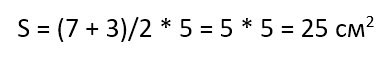
То же самое – миллиметры/квадратные миллиметры, метры/квадратные метры, километры/квадратные километры и так далее.

Доказательство теоремы о площади трапеции

Любая формула в геометрии требует доказательства. И в нашем случае, формулы вычисления площади трапеции также доказывают во время уроков.

Возьмем для примера трапецию:

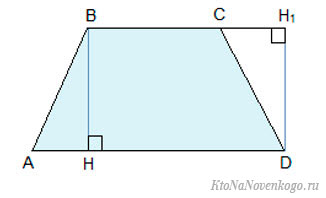
В ней AD и BC – основания, BH – высота. Нам надо доказать, что:

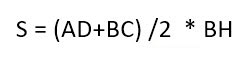
Доказательство строится на том, что если провести диагональ BD, то она разделит нашу трапецию на два треугольника. Это будут треугольники ABD и BCD.

И чтобы получить площадь нашей трапеции, нужно посчитать отдельно площади этих треугольников и сложить их.

А как вычислять площадь треугольника, мы уже знаем (или должны знать, согласно школьному курсу). Надо перемножить длину его основания и высоту и поделить на два.

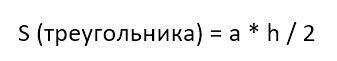
У треугольника ABD высота – это BH. А у треугольника BCD в силу его выпуклости нам пришлось продлить зрительно основание BC, чтобы получить высоту DH1.

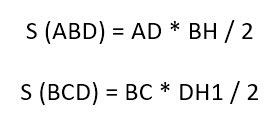
Но в случае с трапецией высоты равны, то есть BH = DH1. И тогда формулу площади для второго треугольника можно заменить на:

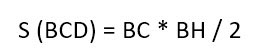
И наконец, с учетом всего вышесказанного начинаем вычислять площадь нашей трапеции. Она равна:

Как часто говориться на уроках геометрии – что и требовалось доказать!

Извиняемся за столь подробное описание доказательства. Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.

Как еще можно найти площадь трапеции (другие формулы)

На этот раз мы уже не будем приводить подробные доказательства каждой из формул. Иначе это займет слишком много времени и места. Просто поверьте, все они правильные и по ним можно вычислить площадь трапеции.

По высоте и средней линии

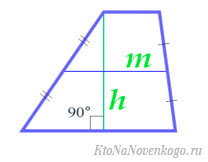
Средняя линия – это та, которая делит боковые стороны трапеции на две равные части. Формула площади выглядит совсем просто:

По четырем сторонам

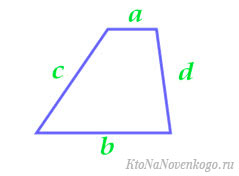
Тут формула гораздо сложнее:

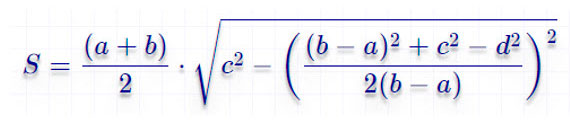
Площадь трапеции через диагонали

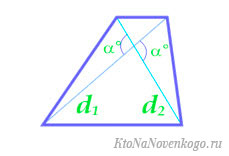
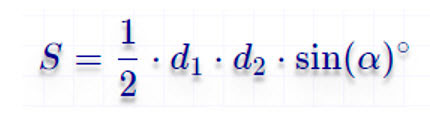
По основанию и углам при нем

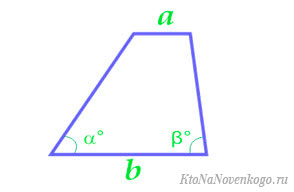
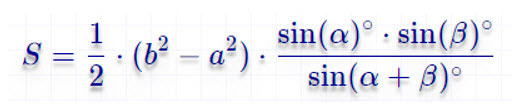
Формулы площади для равнобедренной трапеции

Равнобедренная трапеция – та, у которой боковые стороны равны. А соответственно, они еще и соприкасаются с основаниями под одинаковыми углами.

Это частный случай, и для него верны все перечисленные формулы. Но с учетом равенства сторон и углов формулы заметно упрощаются.

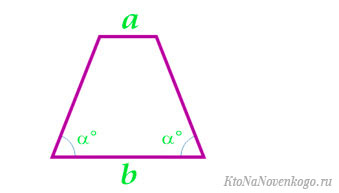
По четырем сторонам

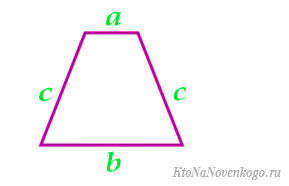
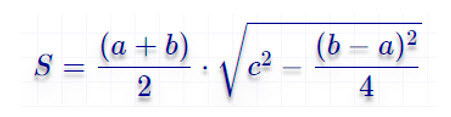
По малому основанию, боковой стороне и углу у большого основания

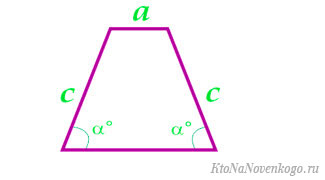
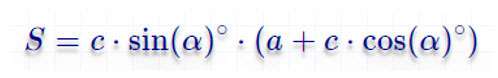
По большому основанию, углу при нем и боковой стороне

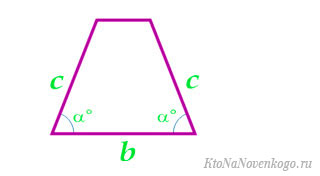
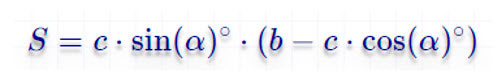
По основаниям и углам

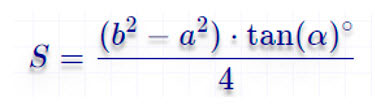
Как видите, формулы громоздкие и весьма сложные сами по себе. Без калькулятора здесь точно не обойтись. С другой стороны, они крайне редко применяются. И служат скорее дополнительными средствами.

Вот и все, что мы хотели рассказать о том, как вычислять площадь трапеции.

Эта статья относится к рубрикам:

Комментарии и отзывы (1)

Теперь любой школьник сможет блеснуть знаниями перед учителем, продемонстрировав несколько способов нахождения площади трапеции. Я уже далеко не школьник, но тоже было интересно.

Читайте также: