Сообщение на тему овал

Обновлено: 30.06.2024

В овал Симметричный определяется как плоская замкнутая кривая, которая имеет две перпендикулярные оси симметрии - одну большую и одну вспомогательную - и состоит из двух дуг окружности, равных два на два.

Таким образом, его можно нарисовать с помощью циркуля и нескольких ориентиров на одной из линий симметрии. В любом случае, есть несколько способов его нарисовать, как мы увидим позже.

Это очень знакомая кривая, поскольку она распознается как контур эллипса, который является частным случаем овала. Но овал - это не эллипс, хотя иногда он очень похож на него, так как его свойства и расположение различаются. Например, эллипс не строится с помощью компаса.

характеристики

Овал находит самое разнообразное применение: архитектура, промышленность, графический дизайн, часовое производство и ювелирные изделия - вот лишь несколько областей, в которых его использование особенно важно.

Наиболее выдающимися характеристиками этой важной кривой являются следующие:

-Он относится к группе технических кривых: он начертан путем образования дуг окружности с помощью циркуля.

-Все его точки находятся в одной плоскости.

-Отсутствие изгибов или завязок.

-Его путь непрерывен.

-Изгиб овала должен быть плавным и выпуклым.

-При рисовании линии, касательной к овалу, все она находится на одной стороне линии.

-Овал допускает не более двух параллельных касательных.

Примеры

Существует несколько методов построения овалов, для которых требуется использование линейки, квадрата и циркуля. Далее мы упомянем некоторые из наиболее часто используемых.

Построение овала из концентрических кругов

На рисунке 2 выше показаны две концентрические окружности с центром в начале координат. Большая ось овала равна диаметру внешней окружности, а малая ось соответствует диаметру внутренней окружности.

-Произвольный радиус проведен до внешней окружности, которая пересекает обе окружности в точках P₁ И п₂.

-Точка P проецируется₂ по горизонтальной оси.

-Точно так же проецируется точка P₁ по вертикальной оси.

-Пересечение обеих линий проекции является точкой P и принадлежит овалу.

-Все точки на этом участке овала можно проследить таким образом.

- Остальная часть овала прорисовывается аналогичной процедурой, проводимой в каждом квадранте.

Упражнения

Далее будут рассмотрены другие способы построения овалов с учетом определенного начального измерения, которое определит их размер.

- Упражнение 1

С помощью линейки и циркуля нарисуйте овал, известный как его большая ось, длиной 9 см.

Решение

На Рисунке 3, показанном ниже, получившийся овал отображается красным цветом. Особое внимание следует обратить на пунктирные линии, которые являются вспомогательными конструкциями, необходимыми для рисования овала, большая ось которого указана. Мы собираемся указать все необходимые шаги, чтобы добраться до окончательного чертежа.

Шаг 1

Проведите отрезок AB длиной 9 см с помощью линейки.

Шаг 2

Разделите отрезок AB, то есть разделите его на три отрезка равной длины. Поскольку исходный сегмент AB составляет 9 см, сегменты AC, CD и DB должны иметь размер 3 см каждый.

Шаг 3

С помощью циркуля, центрирующего в точке C и открывающего CA, рисуется вспомогательная окружность. Аналогичным образом вспомогательная окружность с центром D и радиусом DB рисуется с помощью циркуля.

Шаг 4

Отмечаются пересечения двух вспомогательных окружностей, построенных на предыдущем шаге. Мы называем это точками E и F.

Шаг 5

С помощью правила нарисованы следующие лучи: [FC), [FD), [EC), [ED).

Шаг 6

Лучи предыдущего шага пересекают две вспомогательные окружности в точках G, H, I, J соответственно.

Шаг 7

Если центр циркуля выполнен в F, а при раскрытии (или радиусе) FG дуга нарисована. GH. Аналогичным образом с центром в точке E и радиусе EI рисуется дуга. IJ.

Шаг 8

Объединение арок ГДж, JI, IH Y HG они образуют овал с большой осью 9 см.

Шаг 9

Приступаем к стиранию (скрытию) вспомогательных точек и линий.

- Упражнение 2.

С помощью линейки и циркуля нарисуйте овал, малая ось которого известна, а его размер равен 6 см.

Решение

На рисунке выше (рисунок 4) показан окончательный результат построения овала (красный), а также промежуточные конструкции, необходимые для его достижения. Шаги, которые были выполнены, чтобы построить овал малой оси 6 см, были следующими:

Шаг 1

Отрезок AB длиной 6 см обведен линейкой.

Шаг 2

С помощью циркуля и линейки проведите биссектрису до сегмента AB.

Шаг 3

Пересечение биссектрисы с отрезком AB дает середину C отрезка AB.

Шаг 4

С помощью циркуля начерчивается окружность центра C и радиус CA.

Шаг 5

Окружность, нарисованная на предыдущем шаге, пересекает биссектрису AB в точках E и D.

Шаг 6

На графике нанесены лучи [AD), [AE), [BD) и [BE).

Шаг 7

С помощью циркуля нарисованы окружности центра A и радиуса AB, а также окружности центра B и радиуса BA.

Шаг 8

Пересечения окружностей, нарисованных на шаге 7, с лучами, построенными на шаге 6, определяют четыре точки, а именно: F, G, H, I.

Шаг 9

С центром в D и радиусом DI рисуется дуга IF. Таким же образом с центром в E и радиусом EG строится дуга GH.

Овал — это замкнутая коробовая кривая, имеющая две оси симметрии и состоящая из двух опорных окружностей одинакового диаметра, внутренне сопряженных дугами (рис. 13.45). Овал характеризуется тремя параметрами: длина, ширина и радиус овала. Иногда задают только длину и ширину овала, не определяя его радиусов, тогда задача построения овала имеет большое множество решений (см. рис. 13.45, а. г).

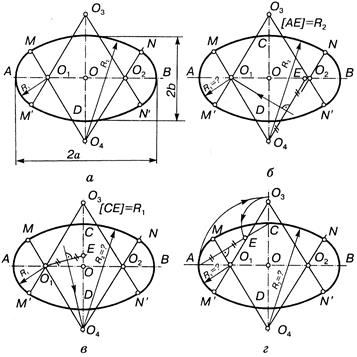
Применяют также способы построения овалов на основе двух одинаковых опорных кругов, которые соприкасаются (рис. 13.46, а), пересекаются (рис. 13.46, б) или не пересекаются (рис. 13.46, в). При этом фактически задают два параметра: длину овала и один из его радиусов. Эта задача имеет множество решений. Очевидно, что R > ОА не имеет верхней границы. В частности R = О₁О₂ (см. рис. 13.46.а, и рис. 13.46.в), а центры О₃ и О₄ определяют, как точки пересечения базовых кругов (см. рис. 13.46,б). Согласно общей теорией точки, сопряжения определяются на прямой, соединяющей центры дуг соприкасающихся окружностей.

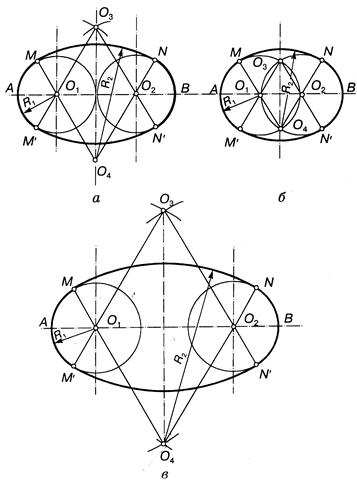
Построение овала с соприкасающимися опорными окружностями (задача имеет множество решений) (рис. 3.44). Из центров опорных окружностей О и 0₁ радиусом, равным, например, расстоянию между их центрами, проводят дуги окружностей до пересечения в точках О₂и О₃.

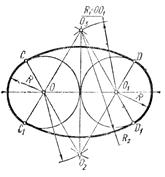
Если из точек О₂и О₃ провести прямые через центры О и O₁, то в пересечении с опорными окружностями получим точки сопряжения С, C₁, D и D₁. Из точек О₂и О₃ как из центров радиусом R₂ проводят дуги сопряжения.

Построение овала с пересекающимися опорными окружностями (задача также имеет множество решений) (рис. 3.45). Из точек пересечения опорных окружностей С₂ и О₃ проводят прямые, например, через центры О и O₁ до пересечения с опорными окружностями в точках сопряжения С, С₁ D и D₁, а радиусами R₂, равными диаметру опорной окружности,— дуги сопряжения.

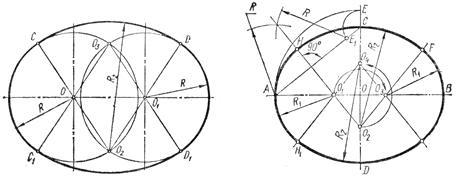
Рисунок 3.45 Рисунок 3.46

Построение овала по двум заданным осям АВ и CD (рис. 3.46). Ниже приведен один из множества вариантов решения. На вертикальной оси откладываются отрезок ОЕ, равный половине большой оси АВ. Из точки С как из центра проводят дугу радиусом СЕ до пересечения с отрезком АС в точке Е₁. К середине отрезка АЕ₁ восстанавливают перпендикуляр и отмечают точки его пересечения с осями овала O₁ и 0₂. Строят точки O₃ и 0₄, симметричные точкам O₁ и 0₂ относительно осей CD и АВ. Точки O₁ и 0₃ будут центрами опорных окружностей радиуса R₁, равного отрезку О₁А, а точки O₂ и 0₄ — центрами дуг сопряжения радиуса R₂, равного отрезку О₂С. Прямые, соединяющие центры O₁ и 0₃ с O₂ и 0₄ в пересечении с овалом определят точки сопряжения.

В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:

1. имеют точку соприкосновения;

3. не пересекаются.

Рассмотрим первый случай. Строят отрезок OO₁=2R, параллельный оси Х, на его концах (точки О и О₁) размещают центры двух опорных окружностей радиуса R и центры двух вспомогательных окружностей радиуса R₁=2R. Из точек пересечения вспомогательных окружностей О₂ и О₃ строят дуги CD и C₁D₁ соответственно. Удаляют вспомогательные окружности, затем относительно дуг CD и C₁D₁ обрезают внутренние части опорных окружностей. На рисунке ъъъ полученный овал выделен толстой линией.

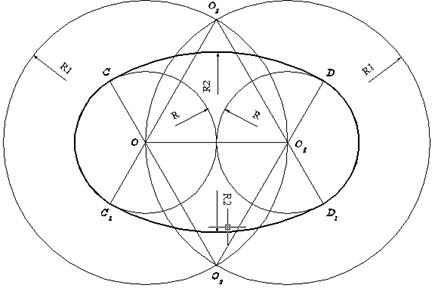
Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса

Рисунок 3.45 Рисунок 3.46

В AutoCAD построение овала производится с помощью двух опорных окружностей одинакового радиуса, которые:

1. имеют точку соприкосновения;

3. не пересекаются.

Рисунок Построение овала с соприкасающимися опорными окружностями одинакового радиуса

An овал (от латинского яйцеклетка, "яйцо") замкнутая кривая в самолет который "слабо" напоминает очертания яйцо. Термин не очень конкретный, но в некоторых областях (проективная геометрия, технический рисуноки т. д.) дается более точное определение, которое может включать как одну, так и две оси симметрии эллипс. В обычном английском этот термин используется в более широком смысле: любая форма, напоминающая яйцо. Трехмерный вариант овала называется яйцевидный.

Содержание

Овал в геометрии

они есть дифференцируемый (гладкий), [1]просто (не самопересекающиеся), выпуклый, закрыто, плоские кривые;
их форма не сильно отличается от эллипс, и
овал обычно имеет ось симметрии, но это не обязательно.

Вот примеры овалов, описанные в другом месте:

Проективная геометрия

В проективная плоскость множество Ω точек называется овал, если:

Любая линия л встречает Ω не более чем в двух точках, и
Для любой точки п ∈ Ω существует ровно одна касательная линия т через п , т.е. т ∩ Ω = п >.

Для конечный плоскостей (т.е. множество точек конечно) есть более удобная характеристика: [2]

Для конечной проективной плоскости порядок п (т.е. любая строка содержит п + 1 баллов) набор Ω точек является овалом тогда и только тогда, когда | Ω | = п + 1 и нет трех точек коллинеарен (по общей линии).

An яйцевидный в проективном пространстве - это множество Ω таких точек, что:

Любая линия пересекает Ω не более 2 баллов,
Касательные в точке покрывают гиперплоскость (и не более того), и
Ω не содержит строк.

в конечный случае только для размерности 3 существуют овоиды. Удобная характеристика:

В 3-х комнатном. конечное проективное пространство порядка п > 2 любой набор точек Ω является яйцевидным тогда и только тогда, когда | Ω | = п 2 + 1 < displaystyle = n ^ +1> и никакие три точки не лежат на одной прямой. [3]

Форма яйца

Технический рисунок

Овал с двумя осями симметрии, построенный из четырех дуг (вверху), и сравнение синего овала и красного эллипса с одинаковыми размерами короткой и длинной осей (внизу).

В технический рисунок, овал фигура, построенная из двух пар дуг с двумя разными радиусы (см. изображение справа). Дуги соединяются в точке, в которой линии касательный чтобы обе соединяющиеся дуги лежали на одной линии, делая стык гладким. Любая точка овала принадлежит дуге с постоянным радиусом (короче или длиннее), но в эллипс, радиус непрерывно меняется.

В общей речи

Наука и образование

Чем отличается эллипс от овала? Данный вопрос часто остается без ответа — хоть эти две фигуры и знакомы всем еще со школьных времен. Но мало кто понимает, в чем разница между ними. И существуют ли вообще какие-либо отличия.

В чем различие?

Официальные определения каждой из фигур звучат достаточно сложно и непонятно.

Но, если откинуть заумные формулы и сложные определения — все намного проще.

Где а — это длинная полуось, b — короткая, а с — фокальное расстояние (от центра до фокуса).

Всем известный круг — это частный вариант эллипса. В этом случае с=0 (т.к. фокус у него один). Полуоси (радиусы) тоже равны.

Построение овалов и эллипсов

Казалось бы, а зачем их вообще строить?

Земная орбита имеет форму эллипса (траектории движения остальных планет и галактик аналогичны).

Практически в любой технике имеются круглые детали — а они при переведении в трехмерную проекцию будут изображаться в форме замкнутых кривых. Подобные примеры можно приводить бесконечно.

Поэтому в технике, космонавтике, астрономии, архитектуре и многих других научных отраслях разнообразные овалы приходится строить регулярно. Эти знания применяют даже люди, далекие от сложных вычислений — например, художники.

Для того чтобы начертить любую из этих фигур, потребуется лишь циркуль, транспортир и линейка. Сам процесс особых сложностей не вызывает, главное внимательность и точность.

На фото ниже приведен пример построения эллипса в аксонометрии (изометрия).

Формулы и интересные факты

Хоть эти две фигуры и встречаются повсеместно, они до конца не изучены. В школьном курсе их проходят довольно поверхностно, не упоминая о возможных трудностях.

Так, казалось бы, простая задача — вычислить периметр — на самом деле невыполнима. Точной формулы не существует. Это связано с тем, что каждая точка имеет свой собственный радиус кривизны.

Школьникам и людям, далеким от точных вычислений, дают приблизительную формулу. Погрешность у такого результата будет велика, но для примитивных целей это допустимо.

В серьезных расчетах используются совсем другие формулы. Но даже они не дают желаемого результата, так как имеют достаточно большие отклонения от реальных значений.

Читайте также: