Сообщение на тему ортогональное проектирование

Обновлено: 28.06.2024

Мы постоянно встречаемся с различными способами проектирования (или, как еще говорят, проецирования) как в математике, так и в быту: оно применяется при изображении пространственных фигур на плоскости, в частности, при фотографировании и в кино; тени от предметов являются их проекциями; на проектировании основано введение координат как на плоскости, так и в пространстве, изготовление чертежей, планов и т.д. Об одном из способов проектирования — параллельном проектировании — уже говорилось в п. 1.9. Сейчас мы рассмотрим самый простой, но наиболее важный из способов проектирования в пространстве — ортогональное проектирование "ортогональный” в переводе и значит — "прямоугольный"). В этом пункте мы будем говорить просто о проектировании, имея в виду ортогональное проектирование.

О проекции точки и проекции наклонной на плоскость уже говорилось в п. 2.1.

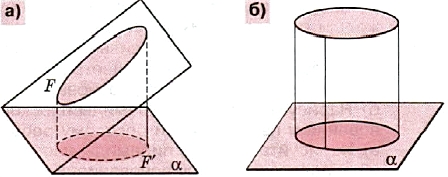
Проекцией же фигуры F на плоскость а называется фигура F, состоящая из проекций всех точек фигуры F на эту плоскость а (рис. 2.32).

Преобразование фигуры F, сопоставляющее каждой точке X фигуры F ее проекцию называется проектированием (или проецированием) фигуры F на

Поскольку все прямые, перпендикулярные к одной плоскости, параллельны друг другу, то ортогональное проектирование на плоскость является частным случаем параллельного проектирования и обладает всеми свойствами параллельного проектирования.

Кроме точек и отрезков, рисуя изображения сферы, цилиндра или конуса, мы будем встречаться с проекцией окружности на плоскость (когда плоскость окружности не перпендикулярна и не параллельна плоскости проекции). Кривая, которая является проекцией окружности в этом случае, называется эллипсом (рис. 2.33). Эллипсом является и параллельная проекция окружности на плоскость (если направление проектирования не параллельно плоскости окружности). Окружность является частным случаем эллипса. Эллипсы обладают многими замечательными свойствами. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии. По эллипсам (эллиптическим орбитам) двигаются планеты вокруг Солнца. Солнце, однако, находится не в центре эллипса — орбиты планеты, а в точке, называемой фокусом эллипса.

Ортогональное проектирование на одну, две и три плоскости широко используется в технике, в черчении. Изображение предмета в проекциях позволяет судить о его устройстве, без чего часто невозможно ни конструирование предмета, ни его изготовление.

В дальнейшем, говоря "проекция" или "проектирование", мы имеем в виду ортогональное проектирование и ортогональную проекцию, если нет специальных оговорок.

На ортогональном проектировании основан такой важный для инженеров раздел прикладной математики, как начертательная геометрия. Начертательная геометрия была создана знаменитым французским математиком Гаспаром Монжем (1746—1818). В ее основе лежит идея о том, что положение любой точки пространства

можно задать ее ортогональными проекциями на две взаимно перпендикулярные плоскости (рис. 2.34).

Повернем плоскость а, вокруг прямой x пересечения плоскостей в направлении, указанном на рисунке 2. 34, до совпадения с плоскостью После такого поворота обе плоскости изобразятся на одном и том же чертеже, называемом эпюром (рис. 2.35).

Прямая X называется осью проекции. Плоскости а, и разбивают все пространство на четыре четверти — квадранта. В зависимости от того, в каком квадранте лежит точка А, изображения ее проекций на эпюре находятся выше или ниже оси проекции (рис. 2.36), причем всегда отрезок перпендикулярен прямой x.

Ясно, что если на эпюре заданы изображения проекций точки А, то они однозначно определяют положение точки А в пространстве.

Тем самым метод Монжа дает возможность строить эпюр по данной фигуре и, наоборот, восстановить фигуру по ее изображению на эпюре. Сам Монж так определял предмет начертательной геометрии:

Начертательная геометрия преследует две цели: во-первых, дать методы для изображения на листе чертежа, имеющего только два измерения, а именно длину и ширину, любых тел природы, имеющих три измерения — длину, ширину и высоту, при условии, однако, что эти тела могут быть точно заданы.

Во-вторых, дать способ на основании точного изображения определять формы тел и выводить все закономерности, вытекающие из их формы и взаимного расположения.

Г. Монж был не только геометром, но и общественным деятелем в период французской буржуазной революции. Он был морским министром и организатором национальной обороны, одним из создателей Политехнической школы в Париже.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Свойства ортогонального проектирования

Свойства, рассматриваемые в школьном курсе математики

Так как ортогональное проектирование – разновидность параллельного, то ему присущи те же свойства.

Свойства параллельной проекции:

проекцией точки является точка;

проекцией прямой является прямая (свойство прямолинейности);

проекцией точки, лежащей на некоторой прямой, является точка, лежащая на проекции данной прямой (свойство принадлежности);

проекциями параллельных прямых являются параллельные прямые (свойство сохранения параллельности);

отношение проекций отрезков, лежащих на параллельных прямых или на одной и той же прямой, равно отношению самих отрезков;

проекция фигуры не меняется при параллельном переносе плоскости проекций.

Кроме того, ортогональное проектирование имеет дополнительно другие свойства:

. Если хотя бы одна из двух перпендикулярных прямых параллельна плоскости проекций, а другая не перпендикулярна этой плоскости, то ортогональные проекции этих прямых перпендикулярны.

Доказательство:

Пусть – перпендикулярные прямые, и – их ортогональные проекции на плоскость (рис. 1), причем . Тогда из следует и из следует . Тогда по теореме о трех перпендикулярах .

. Длина ортогональной проекции отрезка, не перпендикулярного плоскости проекций, равна длине этого отрезка, умноженной на косинус угла его наклона к плоскости проекций (рис. 2):

Ортогональной проекцией отрезка на плоскость является отрезок . Построим отрезок параллельный отрезку . Тогда из прямоугольника и прямоугольного треугольника имеем .

. Площадь ортогональной проекции фигуры, лежащей в плоскости, равна произведению площади этой фигуры на косинус угла между ее плоскостью и плоскостью проекций:

Сначала рассмотрим ортогональную проекцию A ₁ B ₁ C ₁ треугольника ABC , одна сторона которого параллельна плоскости проекций (рис. 3). Если и CD – высота треугольника ABC , то C ₁ D ₁ – высота треугольника A ₁ B ₁ C ₁ (по свойству ). Пусть – угол между плоскостью и плоскостью проекций. Тогда, используя равенство (1.1), получаем,

Пусть теперь ни одна сторона проектируемого треугольника ABC не параллельна плоскости проекций. Тогда через его вершину проведем прямую , разбивающую треугольник ABC на два треугольника (рис. 4). Ее проекция m ₁ разбивает треугольник A ₁ B ₁ C ₁ на два треугольника . И по доказанному

Если данная фигура есть плоский многоугольник, то разобьем его на треугольники. Их ортогональные проекции составят ортогональную проекцию данного многоугольника. Поэтому для него также будет истинно равенство (1.2).

Наконец, пусть данная фигура Ф имеет криволинейную границу. Ее площадь может быть определена как предел последовательности площадей многоугольников, каждый из которых вписан в граничную кривую, при условии, что число вершин (сторон) многоугольник неограниченно увеличивается, а длина наибольшей стороны стремится к нулю. Предполагается, что этот предел существует. В силу того, что теорема истинна для многоугольников и существует предел указанной последовательности площадей многоугольников, она будет истинна и для фигуры Ф.

Данные свойства рассматриваются в школьном курсе математики, например, в учебнике Погорелова А.В., но есть и такие свойства, которые в школьном курсе не рассматриваются.

Формула для вычисления площади боковой поверхности конуса (усеченного конуса) или правильной пирамиды (усеченной пирамиды)

В курсе стереометрии изучают такие теоремы.

Площадь боковой поверхности правильной пирамиды равна произведению периметра основания на половину апофемы: , где (рис. 5).

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему: , где , (рис. 14).

Площадь боковой поверхности конуса равна произведению длины окружности основания на половину образующей: , где (рис. 7).

Площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую: , где , (рис. 8).

Формула для вычисления площади боковой поверхности конуса (усеченного конуса) или правильной пирамиды (усеченной пирамиды) :

где – угол, образованный боковой гранью правильной пирамиды (в том числе и усеченной) с плоскостью нижнего основания, или угол наклона образующей конуса (в том числе и усеченного) к плоскости нижнего основания; и – площади нижнего и верхнего оснований правильной усеченной пирамиды (усеченного конуса) соответственно; для полного конуса и полной правильной пирамиды ; – площадь боковой поверхности конуса (усеченного конуса) или правильной пирамиды (усеченной пирамиды).

Ортогональной проекцией вершины A правильной n - угольной пирамиды на плоскость ее основания является центр О окружности, описанной около основания (рис. 9). Все боковые грани одинаково наклонены к плоскости основания (под углом ). Все боковые грани равновелики, как и их проекции. Из сказанного, следует справедливость формулы (1.3) при .

Основания усеченной пирамиды параллельны. Поэтому площадь S ₁ нижнего основания правильной усеченной пирамиды равна сумме S ₀ , площадей проекций ее боковых граней (на это основание) и площади S ₂ верхнего основания (рис. 10).

Площадь боковой поверхности конуса выражается формулой , где R – радиус основания конуса, L – его образующая (рис. 11). Площадь S ₀ основания конуса определяется по формуле: .

Из двух последних равенств получаем: .

Аналогичным образом доказывается справедливость равенства (1.3) и для усеченного конуса с образующей L и радиусами оснований, равными R и R ₁ (рис. 12):

Данная формула полезна при определении площадей поверхностей многогранников и тел вращения.

Формула для нахождения объема многогранника

Рассмотрим еще одну формулу, не приводящуюся в школьных учебниках.

На рис. 13 изображено тело , которое получено из треугольной призматической поверхности при пресечении ее двумя плоскостями: ABC , перпендикулярной ребрам призматической поверхности, и , при этом .

Формула для нахождения объема многогранника:

Рис. 13 где – площадь ортогональной проекции тела (в данном случае ); , , (рис. 13).

Разделим тело плоскостями и (параллельной ABC ) на три части: треугольную призму и треугольные пирамиды и (рис. 14).

В стереометрии изучаются пространственные фигуры, однако на чертеже они изображаются в виде плоских фигур. Каким же образом следует изображать пространственную фигуру на плоскости? Обычно в геометрии для этого используется параллельное проектирование.
Пусть p - некоторая плоскость, l - пересекающая ее прямая (рис. 1). Через произвольную точку A, не принадлежащую прямой l, проведем прямую, параллельную прямой l. Точка пересечения этой прямой с плоскостью p называется параллельной проекцией точки A на плоскость p в направлении прямой l. Обозначим ее A'. Если точка A принадлежит прямой l, то параллельной проекцией A на плоскость p считается точка пересечения прямой l с плоскостью p .

Таким образом, каждой точке A пространства сопоставляется ее проекция A' на плоскость p . Это соответствие называется параллельным проектированием на плоскость p в направлении прямой l .
Пусть Ф - некоторая фигура в пространстве. Проекции ее точек на плоскость p образуют фигуру Ф', которая называется параллельной проекцией фигуры Ф на плоскость p в направлении прямой l. Говорят также, что фигура Ф' получена из фигуры Ф параллельным проектированием.

3.7. Ортогональное проектирование

Параллельное проектирование, при котором проектирующие прямые перпендикулярны к плоскости проекций, называется ортогональным проектированием .

Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции:

Теоремы о проекциях (с доказательством)

Свойство 1. Если прямая параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой l, то ее проекцией является прямая.
Доказательство. Ясно, что если прямая k параллельна или совпадает с прямой l, то ее проекцией в направлении этой прямой на плоскость p будет точка пересечения прямой l и плоскости p . Пусть k не параллельна и не совпадает с прямой l (рис. 2). Возьмем какую-нибудь точку A на прямой k и проведем через нее прямую a, параллельную l. Ее пересечение с плоскостью проектирования p даст точку A', являющуюся проекцией точки A. Через прямые a и k проведем плоскость a . Ее пересечением с плоскостью p будет искомая прямая k', являющаяся проекцией прямой k .

Свойство 2. Проекция отрезка при параллельном проектировании есть точка или отрезок, в зависимости от того лежит он на прямой, параллельной или совпадающей с прямой l, или нет. Параллельное проектирование сохраняет отношение длин отрезков, лежащих на прямой, не параллельной и не совпадающей с прямой l. В частности, при параллельном проектировании середина отрезка переходит в середину соответствующего отрезка.
Доказательство. Ясно, что если отрезок лежит на прямой, параллельной или совпадающей с прямой l, то его проекцией будет точка. Пусть точки A, B и C лежат на прямой k, не параллельной и не совпадающей с прямой l ; k' – проекция прямой k на плоскость p в направлении прямой l ; A', B', C' – проекции точек A, B и Cсоответственно; a, b, c – соответствующие прямые, проходящие через эти точки и параллельные прямой l (рис. 3). Тогда из теоремы Фалеса планиметрии следует равенство отношений AB : BC = A'B' : B'C'. В частности, если точка B - середина отрезка AC , то B' - середина отрезка A'C' .
Свойство 3. Если две параллельные прямые не параллельны прямой l, то их проекции в направлении l могут быть или параллельными прямыми или одной прямой.
Доказательство. Пусть k ₁ , k ₂ - параллельные прямые, не параллельные прямой l. Так же как и при доказательстве первого свойства, рассмотрим плоскости a ₁ , a ₂ , линии пересечения которых с плоскостью p дают проекции k ₁' , k ₂' прямых k ₁ , k ₂ соответственно (рис. 4). Если плоскости a ₁ и a ₂ совпадают, то проекции прямых k ₁ и k ₂ также совпадают. Если эти плоскости различны, то они параллельны между собой, по признаку параллельности плоскостей (прямая k ₁ параллельна прямой k ₂ , прямаяA ₁ A ₁' параллельна прямой A ₂ A ₂' ). В силу свойства параллельных плоскостей, линии пересечения этих плоскостей с плоскостью p параллельны.

При изображении пространственных фигур на плоскости особенно важно уметь правильно изображать плоские фигуры, поскольку они входят в поверхность основных пространственных фигур. Например, плоские многоугольники являются гранями многогранников, круги - основаниями цилиндров и конусов.
Теорема. Если плоская фигура F лежит в плоскости, параллельной плоскости проектирования p , то ее проекция F' на эту плоскость будет равна фигуре F .
Доказательство. Пусть A , B – точки фигуры F и A ’ , B ’ – их параллельные проекции (рис. 5). Тогда ABB ’ A ’ – параллелограмм. Поэтому параллельный перенос на вектор переводит точку B в B ’ . Поскольку точку B фигуры F можно выбирать произвольно, то этот параллельный перенос переводит фигуру F в фигуру F ’ . Значит фигуры F и F ’ равны.

Ортогональная проекция точки на прямую или на плоскость в стереометрии определяется дословно так же, как проекция точки на прямую в планиметрии. А именно если точка не лежит на данной прямой (плоскости), то ортогональной проекцией точки на прямую (на плоскость) называется основание перпендикуляра, опущенного из этой точки на данную прямую (плоскость).

Если же точка лежит на прямой (на плоскости), то она и есть своя проекция на эту прямую (плоскость) (рис. 109, а). Проекцией же фигуры F на плоскость α называется фигура F', состоящая из проекций всех точек фигуры F на эту плоскость (рис. 109, б). О проекции наклонной на плоскость уже говорилось в п. 6.1.

Поскольку все прямые, перпендикулярные одной плоскости, параллельны друг другу, то ортотональное проектирование на плоскость является частным случаем параллельного проектирования и тем самым обладает всеми свойствами параллельного проектирования.

Кроме точек и отрезков, рисуя изображение сферы, цилиндра или конуса, мы будем встречаться с проекцией окружности на плоскость (когда плоскость окружности не перпендикулярна плоскости проекции). Кривая, которая является проекцией окружности в этом случае, называется эллипсом (рис. 110, а). Эллипсом является и параллельная проекция окружности на плоскость (если направление проектирования не параллельно плоскости окружности). Если плоскость окружности параллельна плоскости проекции, то проекцией, очевидно, является равная ей окружность (рис. 110, б). Поэтому окружность является частным случаем эллипса. Эллипсы обладают многими замечательными свойствами. Эллипс имеет центр симметрии и две взаимно перпендикулярные оси симметрии. По эллипсам (эллиптическим орбитам) двигаются планеты вокруг Солнца. Солнце, однако, находится не в центре эллипса — орбиты планеты, а в точке, называемой фокусом эллипса.

Ортогональное проектирование на одну, две и три плоскости широко используется в технике, в черчении. Изображение предмета в проекциях позволяет судить о его устройстве, без чего невозможно ни конструирование предмета, ни его изготовление.

Начертательная геометрия была создана знаменитым французским математиком Гаспаром Монжем (1746—1818). В её основе лежит идея о том, что положение любой точки пространства можно задать её ортогональными проекциями на две взаимно перпендикулярные плоскости а₁ и а₂ (рис. 111).

13.2 Теорема о трёх перпендикулярах

Вы уже давно знаете, что перпендикуляр, опущенный из точки на прямую, короче любой наклонной, соединяющей эту точку с точкой данной прямой. Вы знаете и аналогичное свойство перпендикуляра, опущенного на плоскость. Эти два минимальных свойства перпендикуляра объединяет следующая важная теорема:

Теорема 16 (о трёх перпендикулярах). Наклонная к плоскости перпендикулярна прямой, лежащей в этой плоскости, тогда и только тогда, когда проекция наклонной перпендикулярна этой прямой.

Доказательство. Пусть даны наклонная АС к плоскости а, её проекция ВС на эту плоскость и прямая а, лежащая в плоскости а и проходящая через точку С (рис. 112, а).

В теореме два утверждения: 1) если AC ⊥ a, то ВС ⊥ а; 2) обратно, если ВС ⊥ а, то АС ⊥ а.

Докажем их. Возьмём переменную точку X прямой а (рис. 112,6) и рассмотрим две величины АХ 2 и ВХ 2 . Так как АВ ⊥ а, то треугольник АВХ прямоугольный. Поэтому АХ 2 = АВ 2 + ВХ 2 . Значит, эти величины отличаются на постоянное слагаемое h = AB2:

AX 2 = BX 2 + h. (1)

Пусть AC ⊥ a. Тогда перпендикуляр АС к прямой а короче любой наклонной АХ к этой прямой. Значит, и отрезок ВС короче любого отрезка ВХ, когда Х ≠ С. Поэтому ВС ⊥ a. Первое утверждение доказано. Докажем второе.
Пусть ВС ⊥ а. Тогда перпендикуляр ВС к прямой а короче любой наклонной ВХ к этой прямой. Поэтому и АС ≤ АХ, если Х ≠ С. Следовательно, AC ⊥ a.

В доказанной теореме рассматриваются три перпендикуляра: АВ ⊥ α, AC ⊥ a, ВС ⊥ a. Отсюда и её название — теорема о трёх перпендикулярах. Эта теорема связывает также проектирование на прямую и проектирование на плоскость. Согласно этой теореме проекцию точки А на прямую а — точку С — можно получить и так: сначала спроектировать точку А на плоскость α в точку В, а затем спроектировать точку В на прямую а. В результате получим ту же самую точку С.

13.3 Расстояние от точки до фигуры

Расстояние от точки до фигуры измеряется по кратчайшему пути. Поэтому расстоянием от данной точки А до фигуры F называется расстояние от этой точки до ближайшей к А точке фигуры F. Точка фигуры F, ближайшая к А, — это такая точка B ∈ F (рис. 113), что для всех точек X фигуры F |АВ|≤ |АХ|.

Иначе говоря, если точка А не принадлежит фигуре F, то отрезок АВ — кратчайший из всех отрезков АХ, соединяющих точку А с точками фигуры F. (Если же A ∈ F, то ясно, что точка А оказывается ближайшей к самой себе. В дальнейшем случай, когда A ∈ F, мы не рассматриваем.)

Расстояние от точки А до фигуры F обозначаем | AF |.

Расстояние от точки А до прямой а равно длине перпендикуляра, опущенного из точки А на прямую а. Обозначаем его | Аа |.
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость, или, что то же, расстоянию от точки до её проекции на плоскость.

Понятие ближайшей точки даёт возможность получить интересное обобщение теоремы о трёх перпендикулярах.

Заменим в этой теореме прямую а на произвольную фигуру F в плоскости α (рис. 114).

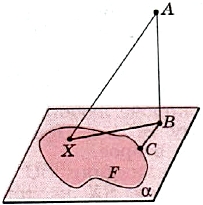
Пусть X — переменная точка фигуры F. Из равенства (1) делаем тот же вывод о наименьших расстояниях АХ и ВХ; они становятся наименьшими одновременно.

Получаем такое обобщение теоремы о трёх перпендикулярах:

Теорема (о ближайшей точке). Пусть фигура F лежит в плоскости α, А — некоторая точка, не принадлежащая α, и В — её проекция на α. Точка фигуры F будет ближайшей к точке А тогда и только тогда, когда она является ближайшей к её проекции В.

Из теоремы о ближайшей точке следует такое утверждение: из данной точки А в ближайшую точку плоской фигуры F можно попасть так: сначала в ближайшую к А точку В самой плоскости, а потом из точки В в ближайшую к ней точку фигуры F.
Теорема о трёх перпендикулярах оказалась, как мы видим, только частным случаем теоремы о ближайшей точке, относящейся к любой плоской фигуре. При этом доказательство её ничуть не сложнее. Это примечательно!

Один из моментов в развитии математики состоит в том, что результаты, которые прежде относились к более специальным фигурам, уравнениям, функциям или иным объектам математики, обобщаются позже на гораздо более общие объекты. Теорема о трёх перпендикулярах восходит к древним грекам (но доказывали они её по-другому), а теорема о ближайшей точке принадлежит геометрии XX в.

13.4 Площадь проекции многоугольника

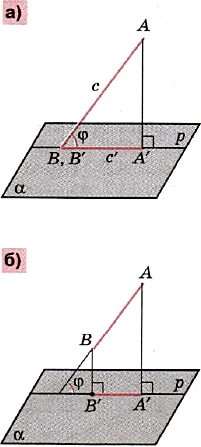
Вам хорошо известно, что длина с отрезка АВ и длина с' его проекции А'В' на некоторую прямую р (или плоскость α) связаны равенством

где φ — угол наклона прямой АВ к прямой р или к плоскости α (рис. 115). Если φ ≠ 0° или φ ≠ 90°, то равенство (2) выражает длину катета с' прямоугольного треугольника через длину с его гипотенузы и косинус прилежащего к катету острого угла φ.

Теорема о трёх перпендикулярах позволяет доказать аналогичную формулу

для площади S некоторой фигуры F и площади S её проекции F' на некоторую плоскость α. Угол φ в равенстве (3) — это угол наклона плоскости β, в которой лежит фигура F, к плоскости α (рис. 116).

Равенство (3) очевидно для случая, когда φ = 90° (в этом случае F' лежит на прямой и S' = 0, а также cos 90° = 0), и для случая, когда φ = 0° (в этом случае плоскости α и β параллельны или совпадают, фигура F' равна фигуре F и cos 0° = 1). Поэтому будем считать, что угол φ острый.

Равенство (3) сначала докажем для случая, когда фигура F — некоторый треугольник ABC. Прямую, по которой пересекаются плоскости α и β, обозначим через а. Если сторона АВ лежит на α, то высота С'Н треугольника ABC' является проекцией высоты СН треугольника ABC (по теореме о трёх перпендикулярах, рис. 117, а).

Тогда С'Н = СН cos φ и S' = 0,5АВ • C'H = 0,5ABC • CH cos φ = S cos φ.

Для случая, когда АВ лежит на а, равенство (3) доказано.

Если сторона АВ параллельна прямой а, то проведём через прямую АВ плоскость γ, параллельную плоскости α, и сведём доказательство равенства (3) к уже рассмотренному случаю (рис. 117, б).

Пусть у треугольника ABC нет сторон, параллельных прямой а (или лежащих на α). Тогда через одну из его вершин (например, через вершину А) проходит прямая р, параллельная прямой а, которая разбивает треугольник ABC на два треугольника АВР и АСР, у которых уже есть такая сторона АР (рис. 118). Тогда

Равенство (3) доказано для любых треугольников.

Если фигура F — многоугольник, то, разбивая её на треугольники, доказываем равенство (3) аналогично тому, как это было доказано в цепочке равенств (4) (рис. 119).

Наконец, для произвольных фигур F равенство (3) можно доказать, приближая их многоугольными фигурами. Например, площадь S' фигуры, ограниченной эллипсом, который получен проектированием окружности радиуса а, вычисляется по формуле S' = πab у где b — длина проекции радиуса окружности, перпендикулярного прямой пересечения плоскости окружности и плоскости проекции.

Читайте также: