Сообщение числа близнецы 6 класс

Обновлено: 06.07.2024

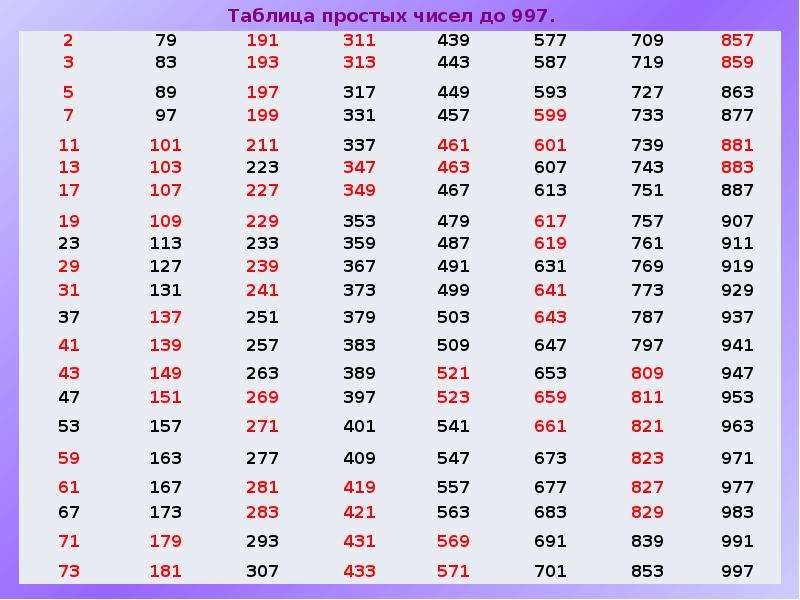
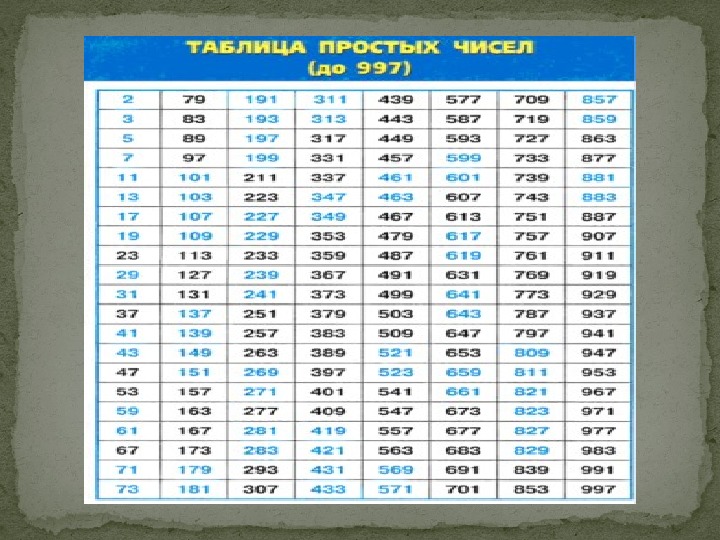
3 (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109),(137, 139), (149, 151), (179, 181), (191, 193), (197, 199), (227, 229), (239, 241), (269, 271), (281, 283), (311, 313), (347, 349), (419, 421), (431, 433), (461, 463), (521, 523), (569, 571), (599, 601), (617, 619), (641, 643), (659, 661), (809, 811), (821, 823), (827, 829), (857, 859), (881, 883) Первые простые числа-близнецы

5 Близнецы могут собираться в скопления, образуя четвёрки вида (n-4, n-2, n+2,n+ 4),например (5, 7, 11, 13, ) или ( 11, 13, 17, 19, ). Как много таких скоплений – пока неизвестно. Близнецы могут собираться в скопления, образуя четвёрки вида (n-4, n-2, n+2,n+ 4),например (5, 7, 11, 13, ) или ( 11, 13, 17, 19, ). Как много таких скоплений – пока неизвестно.

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Числа-близнецы – простые числа, между которыми в натуральном ряду чисел находится только одно число. В математике простые числа определяются как числа, делящиеся на себя и на единицу. Пара таких чисел, расположенных рядом, называются числами-близнецами.Вопрос о том, бесконечно ли множество простых чисел-близнецов, был одним из величайших открытых вопросов в теории чисел в течение многих лет.работа ученика

ЧИСЛА-БЛИЗНЕЦЫ

ЧИСЛА-БЛИЗНЕЦЫ

Что такое простые числа- близнецы? Числа-близнецы – простые числа, между которыми в натуральном ряду чисел находится только одно число. В математике простые числа определяются как числа, делящиеся на себя и на единицу. Пара таких чисел, расположенных рядом, называются числами-близнецами.

ЧИСЛА-БЛИЗНЕЦЫ

Пример чисел-близнецов. В качестве примера приведём несколько таких пар: 2, 3, 5, 7, 11, 13, 17, 19, 29, 31, 41, 43, 59, 61, 71, 73… Этих чисел бесконечное количество.

ЧИСЛА-БЛИЗНЕЦЫ

ЧИСЛА-БЛИЗНЕЦЫ

Самые большие, известные простые числа-близнецы. 3756801695685 × 2 <666669>(200700 цифр) 65516468355 × 2 (100355 цифр) 70965694293 × 2 (60219 цифр) 66444866235 × 2 (60218 цифр) 4884940623 × 2 (59855 цифр) 2003663613 × 2 (58711 цифр) 38529154785 × 2 (52165 цифр) 194772106074315 × 2 (51780 цифр) 100314512544015 × 2 (51780 цифр)

ЧИСЛА-БЛИЗНЕЦЫ

ЧИСЛА-БЛИЗНЕЦЫ

17 апреля 2013 года, Итан Чжан анонсировал доказательство того, что существует бесконечно много пар простых чисел, которые отличаются не более чем на 70 миллионов. Работа была принята в Анналы математики в мае 2013 года. 30 мая 2013 года австралийский математик Скотт Морисон опубликовал запись в блоге SBSEMINAR, объединяющем нескольких недавних аспирантов- математиков Беркли Морисон с помощью компьютерных вычислений и снизил оценку до 59 470 640[5]. Буквально через несколько дней австралийский математик, лауреат Филдсовской медали Теренс Тао доказал, что граница может быть уменьшена на порядок — до 4 982 086[5]. Впоследствии он предложил проекту Polymath совместными усилиями оптимизировать границу.

ЧИСЛА-БЛИЗНЕЦЫ

ЧИСЛА-БЛИЗНЕЦЫ

ЧИСЛА-БЛИЗНЕЦЫ

Эратосфен - Греческий математик, астроном, географ, филолог и поэт. Ученик Каллимаха, с 235 г. до н. э. - глава Александрийской библиотеки. Первый известный учёный, вычисливший размеры Земли.

Если смотреть на первые элементы последовательности простых чисел, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, кажется, что вот-вот поймешь ее секрет, увидишь зависимость, общую формулу, дающую следующие члены - то оказывающиеся по-соседству, то прыгающие сразу через несколько позиций натурального ряда. На самом деле, такой формулы не существует. При всей кажущейся простоте, в математике немного более загадочных и труднопостижимых объектов, чем простые числа.

Но иногда соседние числа идут буквально друг за другом. С помощью современного компьютера мы можем найти практически любое количество простых чисел, но этого мало, для того, чтобы понять, как они ведут себя еще дальше, для того, чтобы сделать выводы о поведении их ряда в целом. Именно с распределением простых чисел связано множество интересных гипотез.

Одна из них — гипотеза о простых числах-близнецах: существует бесконечное количество простых чисел, отличающихся друг от друга на 2. Таких пар много в начале ряда: 3 и 5, 5 и 7, 11 и 13, 17 и 19, 29 и 31. Наибольшие известные на сегодняшний день простые близнецы, полученные с помощью компьютерных вычислений, это 3,756,801,695,685×2 666,669 — 1 и 3,756,801,695,685×2 666,669 + 1. Но будут ли простые близнецы встречаться сколь угодно далеко, до сих пор неизвестно.

На самом деле до недавнего времени не было ответа на более простой вопрос: верно ли, что расстояния между соседними простыми числами растут с ростом простых чисел? Используя аналогию с линейкой, верно ли, что для любой линейки, начиная с какого-то момента, она начнет зацеплять не больше одного простого числа за раз? Разумеется, если гипотеза о числах близнецах верна, то ответ на этот вопрос отрицательный.

Ответ (разумеется, отрицательный) на этот более простой вопрос впервые дал малоизвестный математик Итан Чжан из Университета Нью-Гэмпшира. Работа Чжана, опубликованная в мае 2013 года в научном журнале Annals of Mathematics оказалась полнейшей неожиданностью для математического сообщества. Чжану удалось сделать самый существенный прорыв в понимании поведения последовательных простых чисел за последние несколько сотен лет.

Чжан доказал, что существует бесконечное количество пар подряд идущих простых чисел, отстоящих друг от друга на 70 миллионов. 70 000 000 это еще не 2, что требовалось бы для доказательства гипотезы о простых близнецах, но уже и далеко не бесконечность.

70 000 000: Итан Чжан

В основе доказательства Чжана лежит специальный объект — так называемый подтверждающий гребень.

Назовем гребнем упорядоченное множество различных неотрицательных целых чисел ₁. h_k>. Его можно представлять себе как расческу шириной в h_k зубьев, у которой выломаны все зубья, кроме тех, которые стоят на позициях с номерами h_i. Мы хотим двигать гребень по натуральному ряду и смотреть, попадают ли одновременно все его зубья на простые числа, другими словами, являются ли для данного n все числа вида n+h₁. n+h_k простыми.

Возьмем простейший пример, гребень вида . В таком гребне k = 2, h₁ = 0, h₂=1. Число 1 по определению не считается простым, так что гребень интересно примерять к натуральным числам начиная со второй позиции. Тогда его зубцы укажут на 2 и 3 — оба эти числа простые. Но очевидно, что если двигать расческу дальше, то один из ее зубцов будет обязательно указывать на четное число большее 2-х, которое не является простым. Неинтересный случай.

Гребень называется подтверждающим, если для любого простого числа p множество остатков от деления h_i на p состоит менее чем из p различных чисел. По сути, это свойство гребня — необходимое условие для того, чтобы при движении гребня по натуральноу ряду его зубцы вида n+h₁, . , n+h_k могли бы попадать на наборы, состоящие только из простых чисел. Почему?

Давайте предположим, что наш гребень — не подтверждающий. Значит, для какого-то простого числа p остатки от деления h_i на p пробегают все значения от 0 до p-1. Продвинем гребень на любую позицию n>p. Его зубья указывают на числа n+h₁. n+h_k. Пусть остаток от деления n на p равен m. Так как гребень у нас не подтверждающий, среди в наборе зубцов есть один, скажем h_k, остаток от деления которого на p равен p-m. Тогда в сдвинутом на n-ю позицию гребне этот зубец укажет на число n+h_k, остаток которого при делении на p равен p-m+m = p. Значит, этот зубец указывает на число делящееся на p и строго большее его, это число — составное. Таким образом мы доказали, что хотя бы один зубец не подтверждающего гребня, сдвинутого на любую позицию n>p, приходится на составное число.

Кстати, гребень - как раз самый простой пример не подтверждающего гребня. Остатки от деления его зубьев на наименьшее простое число, 2, пробегают все значения - и 0 и 1. Именно поэтому куда не подвинь гребень на натуральном ряду начиная со второй позиции, один из зубцов будет составным числом.

Тут, конечно, возникает вопрос - а существуют ли вообще подтверждающие гребни? Ответить на этот вопрос не очень просто, поэтому читателю придется поверить нам на слово: такие гребни есть. Более того, главная теорема, доказанная Итаном Чжаном состоит в том, что если H - некоторый подтверждающий гребень, в котором есть как минимум 3,5 миллиона зубцов, то при его сдвигах по натуральному ряду будет бесконечно много ситуаций, когда хотя бы два зубца указывают на простые числа. Из этого следует, что существует бесконечно много пар подряд идущих простых чисел, расстояние между которыми не превышает 70 миллионов.

Действительно, чтобы проверить этот переход достаточно построить подтверждующий гребень, в котором будет не меньше 3.5 миллионов зубцов, но расстояние между крайними зубцами не превышает 70 миллионов. Оказывается, что гребень, состоящий из зубьев, стоящих только на простых позициях, но больших, чем общее число зубцов в нем, является подтверждающим. А сколько можно найти простых чисел между 3,5x10 6 и 7x10 7 ? Согласно неравенствам, доказанном Пьером Дюсаром в 2010 году п(x), число простых чисел, не превышающих данное число x, при достаточно больших x (как в нашем случае) можно оценить с двух сторон вот таким образом:

Читайте также:

  
• Турецкий марш моцарт сообщение
  
• Сообщение о вредной привычке курение 6 класс
  
• Специальные методы обследования в хирургии сообщение
  
• Жесткость воды и способы ее устранения химия 9 класс сообщение
  
• Передать сообщение за газ