Решение задач на множества сообщение

Обновлено: 25.06.2024

Второй блок содержит задачи, для решения которых используются круги (диаграммы) Эйлера.

Весь материал разработки сопровождается слайдами презентации.

Вложение	Размер
metodicheskaya_razrabotka_po_teme_mnozhestva_i_operacii_nad_nimi._reshenie_zadach_s_pomoshchyu_krugov_eylera._salamatova_a.g.docx	43.04 КБ
prezentaciya_mnozhestva_i_operacii_nad_nimi._reshenie_zadach_s_pomoshchyu_krugov_eylera._salamatova_a.g.pptx	1.7 МБ

Предварительный просмотр:

Методическая разработка по теме:

Современный математический язык более краток и заменяет разговорный язык специальными буквенными и символьными выражениями. Понятия и обозначения языка теории множеств составляет фундамент современного математического языка. Всякий объект, входящий во множество, называют его элементом . Например, если множество – дни недели, то понедельник элемент этого множества.

Блок 1 . Множества и операции над ними.

Презентация. (Слайд 2) Вопросы к слайду 2:

1. Перечислите элементы множеств:

а) арабских цифр; (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)

б) натуральных чисел; (1; 2; 3; 4;…)

в) целых чисел (…-2; -1; 0; 1; 2;…).

2. Как называется множество цветов, стоящих в вазе? (букет).

3. Перечислите элементы множества планет солнечной системы. (Меркурий, Венера, Земля,

Марс, Юпитер, Сатурн, Уран, Нептун).

4.Как называется множество фруктовых деревьев и кустарников растущих у дома? (сад).

5. Приведите примеры множеств, элементами которого являются геометрические фигуры.

6. Какие названия применяют для обозначения множеств животных? (млекопитающие,

земноводные, хладнокровные и т.п.).

7. Перечислите элементы множества видов спорта (футбол, теннис, волейбол и т. п.).

8. Какие названия применяют для обозначения множеств кораблей? (флотилия, эскадра).

Задайте сами множество описанием.

(Слайд 3) Множества обычно обозначают большими буквами латинского алфавита: А, В,

С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных

разделах математики, что для них ввели специальные обозначения:

N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

I - множество иррациональных чисел;

R – множество действительных чисел.

(Слайд 4) Чтобы не забыть, что перечисляемые элементы объединены вместе в

некоторое множество, такое перечисление производят внутри фигурных скобок .

Например, цифры десятичной системы счисления задаются множеством

Если множество состоит из чисел, то при их перечислении иногда удобнее использовать

Элементы множества можно перечислять в произвольном порядке. От изменения порядка

перечисления элементов само множество не меняется. Например, множество гласных букв

Эти множества состоят из одних и тех же элементов, их называют равными , а для записи

Чтобы задать конечное множество , можно просто перечислить все его элементы.

Например, запись А = означает, что множество А состоит из первых шести

Однако задавать множество путем перечисления его элементов удобно только в том

случае, когда их число невелико. Если число элементов множества достаточно велико или

множество бесконечно , то явное перечисление элементов такого множества невозможно.

Способы задания, описания множеств весьма разнообразны. Например, множество

всех квадратов натуральных чисел можно записать , а множество всех

чисел, которые больше 5 и меньше 12 записать

Описав словами некоторое множество, нельзя гарантировать, что найдется хотя бы один

объект, отвечающий этому описанию. Предположим, о множестве С сказано, что оно состоит

из чисел, делящихся на 6, но не делящихся на 3. Таких чисел просто нет. В подобных

случаях множество называют пустым и обозначают символом Ø, в фигурные скобки его не

ставят, так как никакого перечисления элементов пустого множества не происходит.

(Слайд 5) Задание 1. [3]

1) Задайте множество цифр, с помощью которых записывается число:

а) 3254; б) 8797; в) 11000; г) 555555.

2) Задайте множество А описанием:

3) Задание с выбором ответа. Даны множества: М = , Р = , Т = ,

S = . Какое из утверждений неверно?

а) М = Р. б) Р ≠ S. в) М ≠ Т. г) Р = Т.

В математике эти выражения кратко записывают так: х А, где – знак принадлежности .

( знак не принадлежит ). Запись 0 N означает, что нуль не натуральное число.

(Слайд 7) Задание 2. [3; 1]

1. Запишите на символическом языке следующее утверждение:

а) число 10 – натуральное;

б) число – 7 не является натуральным;

в) число – 100 является целым;

г) число 2,5 – не целое.

а) – 5 N; б) -5 Z; в) 2,(45) Q?

(Слайд 8) Возьмем множество А = и В = . Каждый элемент

множества А принадлежит также и множеству В. В таких случаях говорят, что множество А

является подмножеством множества В, и пишут: А В.

Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью

так называемых кругов Эйлера ( Леонард Эйлер российский ученый — математик, механик,

физик и астроном.). Множество изображается в виде некоторого круга, а его элементы

изображаются точками этого круга (рис 1).

Пустое множество считают подмножеством любого множества. А В

Будем считать, что все элементы рассматриваемых множеств Рис. 1

изображать квадратом, а рассматриваемые множества А, В, С, … - подмножества множества

К – кругами (или другими полученными из них фигурами, которые выделим штриховкой).

(Слайд 9) Задание 3. [3; 1]

Поставьте вместо … знак включения ( или ) так, чтобы получилось верное

утверждение: а) А… D; б) А…В; в) С…А; г) С…В.

Верно ли, что: а) А В; б) В С; в) С А; г) С В?

(Слайд 10) Из данных множеств с помощью специальных операций можно образовывать

1) Пересечением множества А и В называют множество, состоящие из всех общих

элементов множеств А и В, т. е. из всех элементов, которые принадлежат

и множеству А, и множеству В (рис. 2). Пересечение множеств А и В

обозначают так: А∩В . Это определение можно записать и так:

А∩В = . Иными словами, пересечение двух А∩В К

множеств - это их общая часть. Например, если А = и Рис. 2

А∩В = . Можно рассматривать пересечение не только двух, но трех, четырех и

т. д. множеств. Пересечение множеств В, С и D обозначают так: В∩С∩D.

(Слайд 11) Задание 4. [3; 1]

Найдите: а) А∩В; б) А∩С; в) С∩В.

2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = .

2) Объединением множеств А и В называют множество, состоящее из всех элементов,

которые принадлежат хотя бы одному из этих множеств – или

множеству А, или множеству В (рис. 3). Объединение множеств

А и В обозначают так: АUВ .

Это определение можно записать и так:

АUВ = . Например, если А = и

рассматривать объединение не только двух, но трех, четырех и т. д. Рис. 3

множеств. Объединение множеств В, С и D обозначают так: ВUСUD.

(Слайд 13) Задание 5. [3; 1]

Найдите: а) АUВ; б) АUС; в) СUВ.

3. Даны три числовых промежутка: А = (7,7; 11), В = [ ; ], С = ( ; 13].

3) Разность А и В это множество элементов А, не принадлежащих В

(рис.4). Разность А и В обозначают так: А\ В . Например,

4) Дополнение множества А обозначают так: Ā (рис. 5).

Дополнение множества до множества К: Ā = К\А.

Например, если А = и

1. а) 10 N; б) -7 N; в) -10 Z; г) 2,5 Z . 2. а) нет; б) да; в) да; 3. а) да; б) нет.

1. а) А D; б)А В; в)С А; г)С В. 2. а) нет; б) нет; в) да; г) да.

Блок 2. Решение задач с помощью кругов (диаграмм) Эйлера.

Чтобы облегчить рассуждения в следующих задачах, воспользуемся кругами Эйлера.

Презентация. (Слайд 16) Портрет Леонарда Эйлера (1707-1783).

(Слайд 17) Задача 1.[3]

Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента.

(Слайд 18) Задача 2.[3]

Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента.

Сколько элементов в множестве А U В?

(Слайд 19) Задача 3.[2]

Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и

другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь

13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?

(Слайд 20) Задача 4.[1]

На школьной спартакиаде каждый из 25 учеников 9 –го класса выполнил норматив или по

бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников

выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько

учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при

условии, что не выполнен норматив по бегу?

(Слайд 21) Задача 5.[3]

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки.

Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются

(Слайд 22) Задача 6.[1]

Каждый из учеников 9-го класса в зимние каникулы ровно два раза был в театре, посмотрев

спектакли А, В или С. При этом спектакли А, В, С видели соответственно 25, 12 и 23

ученика. Сколько учеников в классе?

(Слайд 23) Задача 7.[2]

В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – на

стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион-3; цирк и

стадион -1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а

три ученика не посетили ни одного места?

(Слайд 24) Задача 8.[2]

В одном классе 25 учеников. Из них 7 любят груши, 11 – черешню. Двое любят груши и

черешню; 6 – груши и яблоки; 5 – яблоки и черешню. Но есть в классе два ученика,

которые любят всё и четверо таких, что не любят фруктов вообще. Сколько учеников этого

класса любят яблоки?

(Слайд 25; слайд 26) Задача 9.[1]

На уроке литературы учитель решил узнать, кто из 40 учеников 9 –го класса читал книги А,

В, С. Результаты опроса выглядели так: книгу А прочитали 25 учеников, книгу В – 22

ученика, книгу С – 22 ученика; одну из книг А или В прочитали 33 ученика, одну из книг А

или С прочитали 32 ученика, одну из книг В или С – 31 ученик. Все три книги прочитали 10

учеников. Сколько учеников: а) прочитали только по одной книге; б) прочитали ровно две

книги; в) не прочили ни одной из указанных книг?

(Слайд 27) Задача 10.

На зимних каникулах из 36 учащихся класса только двое просидели дома, а 25 ребят ходили

в кино, 15 – в театр, 17 – в цирк. Кино и театр посетили 11 человек, кино и цирк – 10, театр и

цирк – 4. Сколько ребят побывало и в кино, и в театре, и в цирке?

Задача 2. 9 элементов.

Задача 3. 89 семей.

Задача 4. а) 18 учеников; б) 14 учеников; в) 7 учеников.

Задача 5. 10 школьников.

Задача 6. 30 учеников.

Задача 7. 29 учеников.

Задача 8. 14 учеников.

Задача 9. а) 15 учеников; б) 12 учеников; в) 3 ученика.

Задача 10. 2 ученика.

(Слайд 28) Литература

[1] Алгебра, 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений

/ [А. Г. Мордкович, Л.А. Александрова и др.] -12-е изд., испр. - М.: Мнемозина, 2010.

[2] Занимательная математика. 5 – 11 классы. Авт.- сост. Т.Д. Гаврилова. – Волгоград:

Учитель, 2005. – 96 с.

[3] Математика 6 класс: учеб. для общеобразоват. учреждений / Г.В. Дорофеев, И.Ф.

Шарыгин, С.Б. Суворова и др./; под ред. Г.В. Дорофеева, И.Ф. Шарыгина; Рос. акад. наук,

На математическом кружке вместе с учащимися рассматривался ряд задач, благодаря наглядности которых, процесс решения становится понятным и интересным. На первый взгляд им хочется составить систему уравнений, но в процессе решения остается много неизвестных, что ставит их в тупик. Для того, чтобы уметь решать эти задачи, необходимо предварительно рассмотреть некоторые теоретические разделы теории множеств.

Введем определение множества, а так же некоторые обозначения.

Под множеством мы будем понимать такой набор, группу, коллекцию элементов, обладающих каким-либо общим для них всех свойством или признаком.

Множества обозначим А, В, С…, а элементы множеств а, b, с…, используя латинский алфавит.

Можно сделать такую запись определения множества:

“” – принадлежит;
“=>“ – следовательно;
“ø” – пустое множество, т.е. не содержащее ни одного элемента.

Два множества будем называть равными, если они состоят из одних и тех же элементов

Если любой элемент из множества А принадлежит и множеству В, то говорят, что множество А включено в множество В, или множество А является подмножеством множества В, или А является частью В, т.е. если , то , где “С” знак подмножества или включения.

Графически это выглядит так (рис.1):

Можно дать другое определение равных множеств. Два множества называются равными, если они являются взаимными подмножествами.

Рассмотрим операции над множествами и их графическую иллюстрацию (рис.2).

Объединением множеств А и В называется множество С, образованное всеми элементами, которые принадлежат хотя бы одному из множеств А или В. Слова “или ” ключевое в понимании элементов входящих в объединение множеств.

Это определение можно записать с помощью обозначений:

где “ υ ” – знак объединения,

“ / ” – заменяет слова ”таких что“

Пресечение двух множеств А и В называется множество С, образованное всеми элементами, которые принадлежат и множеству А, и множеству В. Здесь уже ключевое слово “и”. Запишем коротко:

“∩“ – знак пересечения. (рис.3)

Обозначим буквой Е основное или универсальное множество, где A С Е (“”- любо число), т.е. А Е = Е; АЕ =А

Множество всех элементов универсального множества Е, не принадлежащих множеству А называется дополнением множества А до Е и обозначается Ā Е или Ā (рис.4)

Примерами для понимания этих понятий являются свойства:

Свойства дополнения имеют свойства двойственности:

Введем еще одно понятие – это мощность множества.

Для конечного множества А через m (A) обозначим число элементов в множестве А.

Из определение следуют свойства:

Для любых конечных множеств справедливы так же утверждения:

m (AB) =m (A) + m (В) – m (А∩В)

m (A∩B) = m (A) + m (В) – m (АВ)

m (ABC) = m (A) + m (В) + m (С)– m (А∩В) - m (А∩С) – m (В∩С) – m (А∩В∩С).

А теперь рассмотрим ряд задач, которые удобно решать, используя графическую иллюстрацию.

Задача №1

В олимпиаде по математике для абитуриентов приняло участие 40 учащихся, им было предложено решить одну задачу по алгебре, одну по геометрии и одну по тригонометрии. По алгебре решили задачу 20 человек, по геометрии – 18 человек, по тригонометрии – 18 человек.

Сколько учащихся решили все задачи?
Сколько учащихся решили только две задачи?
Сколько учащихся решили только одну задачу?

Задача № 2

Первую или вторую контрольные работы по математике успешно написали 33 студента, первую или третью – 31 студент, вторую или третью – 32 студента. Не менее двух контрольных работ выполнили 20 студентов.

Сколько студентов успешно решили только одну контрольную работу?

Задача № 3

В классе 35 учеников. Каждый из них пользуется хотя бы одним из видов городского транспорта: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 6 учеников, метро и автобусом – 15 учеников, метро и троллейбусом – 13 учеников, троллейбусом и автобусом – 9 учеников.

Сколько учеников пользуются только одним видом транспорта?

Решение задачи № 1

m (Е) = 40
m (А) = 20
m (В) = 18
m (С) = 18
m (А∩В) = 7
m (А∩С) = 8
m (В∩С) = 9

m (АВС) = 3 => m (АВС) = 40 – 3 = 37

Обозначим разбиение универсального множества Е множествами А, В, С (рис.5).

К 1 – множество учеников, решивших только одну задачу по алгебре;

К 2 – множество учеников, решивших только две задачи по алгебре и геометрии;

К 3 – множество учеников, решивших только задачу по геометрии;

К 4 – множество учеников, решивших только две задачи по алгебре и тригонометрии;

К 5 – множество всех учеников, решивших все три задачи;

К 6 – множество всех учеников, решивших только две задачи, по геометрии и тригонометрии;

К 7 – множество всех учеников, решивших только задачу по тригонометрии;

К 8 – множество всех учеников, не решивших ни одной задачи.

Ответ:

5 учеников решили три задачи;

9 учеников решили только по две задачи;

23 ученика решили только по одной задаче.

С помощью этого метода можно записать решения второй и третьей задачи так:

m (АВ) = 33
m (АС) = 31
m (ВС) = 32
m (К 2 ) + m (К 4 ) + m (К 6 ) + m (К 5 ) = 20

Ответ:

Только одну контрольную работу решили 18 учеников.

m (Е) = 35
m (А∩В∩С)= m (К 5 ) = 6
m (А∩В)= 15
m (А∩С)= 13
m (В∩С)= 9

m (К 2 ) = m (А∩В) - m (К 5 ) = 15-6=9
m (К 4 ) = m (А∩С) - m (К 5 ) = 13-6=7
m (К 6 ) = m (В∩С) - m (К 5 ) = 9-6=3
m (К 1 ) + m (К 3 ) + m (К 7 ) = m (Е) - m (К 4 ) - m (К 2 ) - m (К 6 ) - m (К 5 ) = 35-7-9-3-6=10

Ответ:

Только одним видом транспорта пользуется 10 учеников.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Дискретный анализ

Решение задач

Дискретный анализ - область математики, занимающаяся изучением свойств структур конечного характера, которые возникают как в самой математике, так и в области ее приложений.

Дискретный анализ представляет собой важное направление в математике, имеющее характерные для него предмет исследования, методы и задачи, специфика которых обусловлена, в первую очередь, необходимостью отказа в Д. а. от основополагающих понятий классической математики - предела и непрерывности - и тем, что для многих задач Д. а. сильные средства классической математики оказываются, как правило, мало приемлемыми. Наряду с выделением Д. а. путем указания его предмета, методов и задач можно также охарактеризовать Д. а. посредством перечисления подразделов, составляющих его. К ним, в первую очередь, относятся теория множеств, комбинаторный анализ, графов теория , теория кодирования и декодирования, теория функциональных систем и некоторые другие.

Дискре́тность — свойство, противопоставляемое непрерывности, прерывность. Также можно понять как нечто, изменяющееся между несколькими различными стабильными состояниями или нечто, состоящее из отдельных частей, прерывистость, дробность.

Анализ — метод исследования, характеризующийся выделением и изучением отдельных частей объектов исследования.

Информационная система — система обработки информации и соответствующие организационные ресурсы (человеческие, технические, финансовые и т. д.), которые обеспечивают и распространяют информацию.

Систе́ма — множество элементов, находящихся в отношениях и связях друг с другом, которое образует определённую целостность, единство .

Рефлексивность - отношение R на множестве X называется рефлексивным, если всякий элемент этого множества находится в отношении R с самим собой.

Симметричность - отношение R на множестве X называется симметричным, если для каждой пары элементов множества a,b выполнение отношения aRb влечёт выполнение отношения bRa.

Транзитивность - отношение R на множестве X называется транзитивным, если для любых трёх элементов множества a,b,c выполнение отношений aRb и bRc влечёт выполнение отношения aRc.

Инъекция — отображение множества в множество ( ), при котором разные элементы множества переводятся в разные элементы множества , то есть, если два образа при отображении совпадают, то совпадают и прообразы : .

Биекция — это отображение , которое является одновременно и сюръективным , и инъективным . При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением.

Множество - совокупность различных элементов, мыслимую как единое целое.

Функция – это правило, по которому каждому элементу одного множества (область определения) ставится в соответствие некоторый элемент другого множества (область значения).

Диаграмма Венна (как правило, общепринятое название - диаграмма Эйлера — Венна) — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств .

Отношения – это некоторые связи между элементами множества.

Декартово произведение ( двух множеств) — это множество , элементами которого являются всевозможные упорядоченные пары элементов исходных множеств.

Объедине́ние мно́жеств (тж. су́мма или соедине́ние) — множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств и обычно обозначается , но иногда можно встретить запись в виде суммы .

Разность ( двух множеств) — это теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств и обозначается как , но иногда можно встретить обозначение и .

Дополне́ние — это семейство элементов, не принадлежащих данному множеству.

На этой странице вы найдете готовые примеры по базовому разделу дискретной математики: элементам теории множеств. Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.

Основные темы (множества) : задание множеств, действия с множествами (пересечение, объединение, разность, дополнение); формула включений-исключений и применение для практических задач; декартово произведение множеств, мощность множества, построение диаграмм Эйлера-Венна.

Задачи с решениями о множествах онлайн

Задача 1. Начертите фигуры, изображающие множества , где - вещественная плоскость. Какие фигуры изображают множества ?

Задача 2. Докажите тождество

Задача 3. Установите взаимно однозначное соответствие между всеми прямыми на плоскости и всеми точками координатной оси Ох.

Задача 4. М - подмножество множества натуральных чисел. 10 элементов множества являются простыми числами, а остальные кратны либо 2, либо 3, либо 5. Определить мощность множества , если оно содержит: 70 чисел кратных 2; 60 чисел кратных 3; 80 числе кратных 5; 98 чисел кратных или 2 или 3; 95 чисел кратных или 2 или 5; 102 числа кратных или 3 или 5; 20 чисел, кратных 30.

Задача 5. Проверить справедливость тождеств или включений, используя алгебру множеств и диаграммы Эйлера-Венна.

Задача 6. Записать множества $A, B, C$ перечислением их элементов и найти . если
$A$ - множество корней уравнения $x^2-12x-28=0$,
$B$ - множество делителей числа 28,
$C$ - множество нечетных чисел $X$, таких что $0 \le X \le 7$.

Задача 7. Задано универсальное множество $U=\$ и множества $X=\$, $Y=\$, $Z=\$. Записать булеан множества $X$, любое разбиение множества $Y$, покрытие множества $Z$. Выполнить действия $(X \setminus Y)\cap \bar Z$.

Задача 8. Решить задачу, используя диаграмму Эйлера-Венна.
Четырнадцать спортсменов участвовали в кроссе, 16 – в соревнованиях по плаванию, 10 – в велосипедных гонках. Восемь участников участвовали в кроссе и заплыве, 4 – в кроссе и велосипедных гонках, 9 – в плавании и велосипедных гонках. Во всех трех соревнованиях участвовали три человека. Сколько всего было спортсменов?

Задача 9. Пусть $Р(А)$ – множество всех подмножеств множества $А$. В каждом из следующих упорядоченных множеств укажите все минимальные и все максимальные элементы; найдите наибольший и наименьший элементы, если они есть, или докажите их отсутствие:

Задача 10. В химическом продукте могут оказаться примеси четырёх видов – $a,b,c,d$. Приняв в качестве исходного множества $М = \$, образуйте множество всех его подмножеств $В(М)$. Дайте содержательную интерпретацию этого множества и его элементов. Каким ситуациям соответствуют, в частности, несобственные подмножества?

Решение задач о множествах на заказ

Выполняем для студентов очников и заочников решение заданий, контрольных и практических работ по любым разделам теории множеств. Также оказываем помощь в сдаче тестов. Подробное оформление, таблицы, графики, пояснение, использование специальных программ при необходимости. Стоимость примера от 100 рублей , оформление производится в Word, срок от 2 дней.

Приветствую вас на первом уроке по высшей алгебре, который появился… в канун пятилетия сайта, после того, как я уже создал более 150 статей по математике, и мои материалы начали оформляться в завершённый курс. Впрочем, буду надеяться, что не опоздал – ведь многие студенты начинают вникать в лекции только к государственным экзаменам =)

Вузовский курс вышмата традиционно зиждется на трёх китах:

– математическом анализе (пределы, производные и т.д.)

Множество. Примеры множеств

Множество – это фундаментальное понятие не только математики, но и всего окружающего мира. Возьмите прямо сейчас в руку любой предмет. Вот вам и множество, состоящее из одного элемента.

В широком смысле, множество – это совокупность объектов (элементов), которые понимаются как единое целое (по тем или иным признакам, критериям или обстоятельствам). Причём, это не только материальные объекты, но и буквы, цифры, теоремы, мысли, эмоции и т.д.

Обычно множества обозначаются большими латинскими буквами (как вариант, с подстрочными индексами: и т.п.), а его элементы записываются в фигурных скобках, например:

– множество букв русского алфавита;
– множество натуральных чисел;

ну что же, пришла пора немного познакомиться:
– множество студентов в 1-м ряду

… я рад видеть ваши серьёзные и сосредоточенные лица =)

Множества и являются конечными (состоящими из конечного числа элементов), а множество – это пример бесконечного множества. Кроме того, в теории и на практике рассматривается так называемое пустое множество:

– множество, в котором нет ни одного элемента.

Пример вам хорошо известен – множество на экзамене частенько бывает пусто =)

Принадлежность элемента множеству записывается значком , например:

В абстрактной и не очень алгебре элементы множества обозначают маленькими латинскими буквами и, соответственно, факт принадлежности оформляется в следующем стиле:

– элемент принадлежит множеству .

Вышеприведённые множества записаны прямым перечислением элементов, но это не единственный способ. Многие множества удобно определять с помощью некоторого признака (ов), который присущ всем его элементам. Например:

– множество всех натуральных чисел, меньших ста.

Данное множество можно записать и прямым перечислением:

Ещё примеры:
– и если и студентов в 1-м ряду достаточно много, то такая запись намного удобнее, нежели их прямое перечисление.

– множество чисел, принадлежащих отрезку . Обратите внимание, что здесь подразумевается множество действительных чисел (о них позже), которые перечислить через запятую уже невозможно.

Подмножества

Практически всё понятно из самого названия: множество является подмножеством множества , если каждый элемент множества принадлежит множеству . Иными словами, множество содержится во множестве :

Значок называют значком включения.

Вернёмся к примеру, в котором – это множество букв русского алфавита. Обозначим через – множество его гласных букв. Тогда:

Также можно выделить подмножество согласных букв и вообще – произвольное подмножество, состоящее из любого количества случайно (или неслучайно) взятых кириллических букв. В частности, любая буква кириллицы является подмножеством множества .

Отношения между подмножествами удобно изображать с помощью условной геометрической схемы, которая называется кругами Эйлера.

Пусть – множество студентов в 1-м ряду, – множество студентов группы, – множество студентов университета. Тогда отношение включений можно изобразить следующим образом:

Множество студентов другого ВУЗа следует изобразить кругом, который не пересекает внешний круг; множество студентов страны – кругом, который содержит в себе оба этих круга, и т.д.

Типичный пример включений мы наблюдаем при рассмотрении числовых множеств. Повторим школьный материал, который важно держать на заметке и при изучении высшей математики:

Числовые множества

Как известно, исторически первыми появились натуральные числа, предназначенные для подсчёта материальных объектов (людей, кур, овец, монет и т.д.). Это множество уже встретилось в статье, единственное, мы сейчас чуть-чуть модифицируем его обозначение. Дело в том, что числовые множества принято обозначать жирными, стилизованными или утолщёнными буквами. Мне удобнее использовать жирный шрифт:

Иногда к множеству натуральных чисел относят ноль.

Если к множеству присоединить те же числа с противоположным знаком и ноль, то получится множество целых чисел:

Совершенно понятно, что множество натуральных чисел является подмножеством множества целых чисел:
– поскольку каждый элемент множества принадлежит множеству . Таким образом, любое натуральное число можно смело назвать и целым числом.

И, коль скоро, целые, то сразу же вспомним важные признаки их делимости на 2, 3, 4, 5 и 10, которые будут требоваться в практических вычислениях чуть ли не каждый день:

Целое число делится на 2 без остатка, если оно заканчивается на 0, 2, 4, 6 или 8 (т.е. любой чётной цифрой). Например, числа:
400, -1502, -24, 66996, 818 – делятся на 2 без остатка.

400 – делится на 4 (т.к. 00 (ноль) делится на 4);
-1502 – не делится на 4 (т.к. 02 (двойка) не делится на 4);
-24, понятно, делится на 4;
66996 – делится на 4 (т.к. 96 делится на 4);
818 – не делится на 4 (т.к. 18 не делится на 4).

Самостоятельно проведите несложное обоснование данного факта.

С делимость на 3 чуть сложнее: целое число делится на 3 без остатка, если сумма входящих в него цифр делится на 3.

Проверим, делится ли на 3 число 27901. Для этого просуммируем его цифры:
2 + 7 + 9 + 0 + 1 = 19 – не делится на 3
Вывод: 27901 не делится на 3.

Просуммируем цифры числа -825432:
8 + 2 + 5 + 4 + 3 + 2 = 24 – делится на 3
Вывод: число -825432 делится на 3

Целое число делится на 5, если оно заканчивается пятёркой либо нулём:
775, -2390 – делятся на 5

Целое число делится на 10, если оно заканчивается на ноль:
798400 – делится на 10 (и, очевидно, на 100). Ну и, наверное, все помнят – для того, чтобы разделить на 10, нужно просто убрать один ноль: 79840

Также существуют признаки делимости на 6, 8, 9, 11 и т.д., но практического толку от них практически никакого =)

Следует отметить, что перечисленные признаки (казалось бы, такие простые) строго доказываются в теории чисел. Этот раздел алгебры вообще достаточно интересен, однако его теоремы… прямо современная китайская казнь =) А Вольдемару за последней партой и того хватило…, но ничего страшного, скоро мы займёмся живительными физическими упражнениями =)

Следующим числовым множеством идёт множество рациональных чисел:
– то есть, любое рациональное число представимо в виде дроби с целым числителем и натуральным знаменателем.

Очевидно, что множество целых чисел является подмножеством множества рациональных чисел:

И в самом деле – ведь любое целое число можно представить в виде рациональной дроби , например: и т.д. Таким образом, целое число можно совершенно законно назвать и рациональным числом.

либо
– конечная десятичная дробь,

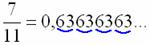
либо
– бесконечная периодическая десятичная дробь (повтор может начаться не сразу).

Полюбуйтесь делением и постарайтесь выполнять это действие как можно реже! В организационной статье Высшая математика для чайников и на других уроках я неоднократно повторял, повторяю, и буду повторять эту мантру:

В высшей математике все действия стремимся выполнять в обыкновенных (правильных и неправильных) дробях

Согласитесь, что иметь дело с дробью значительно удобнее, чем с десятичным числом 0,375 (не говоря уже о бесконечных дробях).

Объединение рациональных и иррациональных чисел образует множество действительных (вещественных) чисел:

– значок объединения множеств.

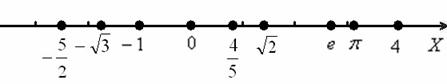
Геометрическая интерпретация множества вам хорошо знакома – это числовая прямая:

Каждому действительному числу соответствует определённая точка числовой прямой, и наоборот – каждой точке числовой прямой обязательно соответствует некоторое действительное число. По существу, сейчас я сформулировал свойство непрерывности действительных чисел, которое хоть и кажется очевидным, но строго доказывается в курсе математического анализа.

С вложениями всё прозрачно: множество рациональных чисел – это подмножество множества действительных чисел:
, таким образом, любое рациональное число можно смело назвать и действительным числом.

Множество иррациональных чисел – это тоже подмножество действительных чисел:

При этом подмножества и не пересекаются – то есть ни одно иррациональное число невозможно представить в виде рациональной дроби.

Существуют ли какие-нибудь другие числовые системы? Существуют! Это, например, комплексные числа, с которыми я рекомендую ознакомиться буквально в ближайшие дни или даже часы.

Ну а пока мы переходим к изучению операций над множествами, дух которых уже материализовался в конце этого параграфа:

Действия над множествами. Диаграммы Венна

Диаграммы Венна (по аналогии с кругами Эйлера) – это схематическое изображение действий с множествами. Опять же предупреждаю, что я рассмотрю не все операции:

1) Пересечение множеств характеризуется логической связкой И и обозначается значком

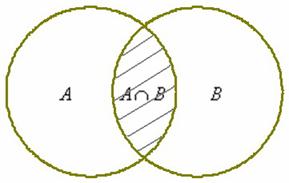
Пересечением множеств и называется множество , каждый элемент которого принадлежит и множеству , и множеству . Грубо говоря, пересечение – это общая часть множеств:

Так, например, для множеств :

Если у множеств нет одинаковых элементов, то их пересечение пусто. Такой пример нам только что встретился при рассмотрении числовых множеств:

Множества рациональных и иррациональных чисел можно схематически изобразить двумя непересекающимися кругами.

Операция пересечения применима и для бОльшего количества множеств, в частности в Википедии есть хороший пример пересечения множеств букв трёх алфавитов.

2) Объединение множеств характеризуется логической связкой ИЛИ и обозначается значком

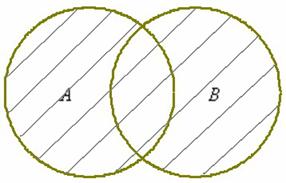
Объединением множеств и называется множество , каждый элемент которого принадлежит множеству или множеству :

Запишем объединение множеств :
– грубо говоря, тут нужно перечислить все элементы множеств и , причём одинаковые элементы (в данном случае единица на пересечении множеств) следует указать один раз.

Но множества, разумеется, могут и не пересекаться, как это имеет место быть с рациональными и иррациональными числами:

В этом случае можно изобразить два непересекающихся заштрихованных круга.

Операция объединения применима и для бОльшего количества множеств, например, если , то:

, при этом числа вовсе не обязательно располагать в порядке возрастания (это я сделал исключительно из эстетических соображений). Не мудрствуя лукаво, результат можно записать и так:

А вот эта разность оказывается пуста: . И в самом деле – если из множества натуральных чисел исключить целые числа, то, собственно, ничего и не останется :)

4) Декартовым (прямым) произведением множеств и называется множество всех упорядоченных пар , в которых элемент , а элемент

Но это чисто для удобства – и в том, и в другом случае пары можно перечислить в каком угодно порядке – здесь важно записать все возможные пары.

А теперь гвоздь программы: декартово произведение – это есть не что иное, как множество точек нашей родной декартовой системы координат .

Задание для самостоятельного закрепления материала:

Выполнить операции , если:

Множество удобно расписать перечислением его элементов.

И пунктик с промежутками действительных чисел:

Краткое решение задачи в конце урока.

Отображение множеств

Отображение множества во множество – это правило, по которому каждому элементу множества ставится в соответствие элемент (или элементы) множества . В том случае если в соответствие ставится единственный элемент, то данное правило называется однозначно определённой функцией или просто функцией.

Функцию, как многие знают, чаще всего обозначают буквой – она ставит в соответствие каждому элементу единственное значение , принадлежащее множеству .

Ну а сейчас я снова побеспокою множество студентов 1-го ряда и предложу им 6 тем для рефератов (множество ):

Установленное (добровольно или принудительно =)) правило ставит в соответствие каждому студенту множества единственную тему реферата множества .

…а вы, наверное, и представить себе не могли, что сыграете роль аргумента функции =) =)

Элементы множества образуют область определения функции (обозначается через ), а элементы множества – область значений функции (обозначается через ).

Построенное отображение множеств имеет очень важную характеристику: оно является взаимно-однозначным или биективным (биекцией). В данном примере это означает, что каждому студенту поставлена в соответствие одна уникальная тема реферата, и обратно – за каждой темой реферата закреплён один и только один студент.

Однако не следует думать, что всякое отображение биективно. Если на 1-й ряд (к множеству ) добавить 7-го студента, то взаимно-однозначное соответствие пропадёт – либо один из студентов останется без темы (отображения не будет вообще), либо какая-то тема достанется сразу двум студентам. Обратная ситуация: если к множеству добавить седьмую тему, то взаимнооднозначность отображения тоже будет утрачена – одна из тем останется невостребованной.

Итак, что же такое функция одной переменной? Функция одной переменной – это правило , которое каждому значению независимой переменной из области определения ставит в соответствие одно и только одно значение .

Задание 2: просмотреть графики основных элементарных функций и выписать на листок биективные функции. Список для сверки в конце этого урока.

Мощность множества

Интуиция подсказывает, что термин характеризует размер множества, а именно количество его элементов. И интуиция нас не обманывает!

Мощность пустого множества равна нулю.

Мощность множества равна шести.

Мощность множества букв русского алфавита равна тридцати трём.

И вообще – мощность любого конечного множества равно количеству элементов данного множества.

…возможно, не все до конца понимают, что такое конечное множество – если начать пересчитывать элементы этого множества, то рано или поздно счёт завершится. Что называется, и китайцы когда-нибудь закончатся.

Само собой, множества можно сравнивать по мощности и их равенство в этом смысле называется равномощностью. Равномощность определяется следующим образом:

Два множества являются равномощными, если между ними можно установить взаимно-однозначное соответствие.

Множество студентов равномощно множеству тем рефератов, множество букв русского алфавита равномощно любому множеству из 33 элементов и т.д. Заметьте, что именно любому множеству из 33 элементов – в данном случае имеет значение лишь их количество. Буквы русского алфавита можно сопоставить не только с множеством номеров
1, 2, 3, …, 32, 33, но и вообще со стадом в 33 коровы.

Примеров очень много. В частности, счётным является множество всех чётных натуральных чисел . Как это доказать? Нужно установить его взаимно-однозначное соответствие с множеством натуральных чисел или попросту пронумеровывать элементы:

Взаимно-однозначное соответствие установлено, следовательно, множества равномощны и множество счётно. Парадоксально, но с точки зрения мощности – чётных натуральных чисел столько же, сколько и натуральных!

Множество целых чисел тоже счётно. Его элементы можно занумеровать, например, так:

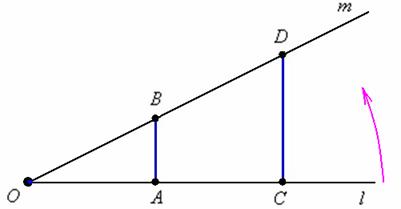
Поскольку между множеством и числовой прямой существует взаимно-однозначное соответствие (см. выше), то множество точек числовой прямой тоже несчётно. И более того, что на километровом, что на миллиметровом отрезке – точек столько же! Классический пример:

Поворачивая луч против часовой стрелки до его совмещения с лучом мы установим взаимно-однозначное соответствие между точками синих отрезков. Таким образом, на отрезке столько же точек, сколько и на отрезке и !

Данный парадокс, видимо, связан с загадкой бесконечности… но мы сейчас не будем забивать голову проблемами мироздания, ибо на очереди основы математической логики, а не философия =)

Спасибо за внимание и успехов вам в учёбе!

Задание 1

2)
– это множество нечётных натуральных чисел:

– все точки координатной плоскости , удовлетворяющие двум указанным неравенствам. Аналогично:

Задание 2 Взаимно-однозначные функции на иллюстрациях урока Функции и графики:

Автор: Емелин Александр

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Читайте также: