Первые алгоритмические машины сообщение

Обновлено: 04.07.2024

1. Определение алгоритма

Во всех сферах своей деятельности, и в особенности в сфере обработки информации, человек сталкивается с различными способами или методиками решения задач. Они определяют порядок выполнения действий для получения желаемого результата – можно трактовать это как первоначальное или интуитивное определение алгоритма. Некоторые дополнительные требования приводят к неформальному определению алгоритма.

Алгоритм – это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых элементарных операций для решения задачи, общее для класса возможных исходных данных. Пусть D – область (множество) исходных данных задачи, а R – множество возможных результатов, тогда мы можем говорить, что алгоритм осуществляет отображение D → R. Поскольку такое отображение может быть не полным, то вводятся следующие понятия: алгоритм называется частичным алгоритмом, если мы получаем результат только для некоторых , и полным алгоритмом, если алгоритм получает правильный результат для всех .

Варианты словесного определения алгоритма принадлежат российским ученым А.Н. Колмогорову и А.А. Маркову.

Алгоритм по Колмогорову – это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.

Алгоритм по Маркову – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.

Следует отметить, что различные определения алгоритма, в явной или неявной форме, постулируют следующий ряд требований:

алгоритм должен содержать конечное количество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;

алгоритм должен выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;

алгоритм должен быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;

алгоритм должен приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.

Однако в начале ХХ века были сформулированы алгоритмические проблемы, положительное решение которых представлялось маловероятным. Решение таких проблем потребовало привлечения новых логических средств. Ведь одно дело доказать существование разрешающего алгоритма – это можно сделать, используя интуитивное понятие алгоритма. Другое дело – доказать отсутствие алгоритма – для этого нужно знать точно, что такое алгоритм.

Начальной точкой отсчета современной теории алгоритмов можно считать работу немецкого математика Курта Гёделя (1931 год – теорема о неполноте символических логик), в которой было показано, что некоторые математические проблемы не могут быть решены алгоритмами из некоторого класса. Общность результата Гёделя связана с тем, совпадает ли использованный им класс алгоритмов с классом всех (в интуитивном смысле) алгоритмов. Эта работа дала толчок к поиску и анализу различных формализаций алгоритма.

Для получения верхних оценок достаточно интуитивного понятия алгоритма. Для этого строится неформальный алгоритм решения конкретной задачи, после чего он формализуется для реализации на подходящей алгоритмической модели. Если показывается, что сложность (время или память) вычисления для этого алгоритма не превосходит значения подходящей функции при всех значениях аргумента, то эта функция объявляется верхней оценкой сложности решения рассматриваемой задачи. В области получения верхних оценок получено много ярких результатов для конкретных задач. Среди них разработаны быстрые алгоритмы умножения целых чисел, многочленов, матриц, решения линейных систем уравнений, которые требуют значительно меньше ресурсов, чем традиционные алгоритмы.

В результате продолжительных теоретических и практических изысканий были сформулированы основные требования к алгоритмам:

Каждый алгоритм имеет дело с данными – входными, промежуточными, выходными. Для того чтобы уточнить понятие данных, фиксируется конечный алфавит исходных символов (цифры, буквы и т.п.) и указываются правила построения алгоритмических объектов. Типичным используемым средством является индуктивное построение. Например, определение идентификатора во многих алгоритмических языках: идентификатор – это либо буква, либо идентификатор, к которому приписана справа либо буква, либо цифра. Слова конечной длины в конечных алфавитах – наиболее обычный тип алгоритмических данных, а число символов в слове – естественная мера объема данных. Другой случай алгоритмических объектов – формулы. Примером могут служить формулы алгебры предикатов и алгебры высказываний.

Алгоритм для размещения данных требует памяти. Память обычно считается однородной и дискретной, т.е. она состоит из одинаковых ячеек, причем каждая ячейка может содержать один символ данных, что позволяет согласовать единицы измерения объема данных и памяти.

Алгоритм состоит из отдельных элементарных шагов, причем множество различных шагов, из которых составлен алгоритм, конечно. Типичный пример множества элементарных шагов – система команд ЭВМ.

Последовательность шагов алгоритма детерминирована, то есть после каждого шага указывается, какой шаг следует выполнять дальше, либо указывается, когда следует работу алгоритма считать законченной.

Алгоритм должен обладать результативностью, то есть останавливаться после конечного числа шагов (зависящего от исходных данных) с выдачей результата. Данное свойство иногда называют сходимостью алгоритма.

Алгоритм предполагает наличие механизма реализации, который по описанию алгоритма порождает процесс вычисления на основе исходных данных. Предполагается, что описание алгоритма и механизм его реализации конечны.

Можно заметить аналогию с вычислительными машинами. Требование 1 соответствует цифровой природе ЭВМ, требование 2 – памяти ЭВМ, требование 3 – программе машины, требование 4 – её логической природе, требования 5, 6 – вычислительному устройству и его возможностям.

Следует ли фиксировать конечную границу для размера входных данных?

Следует ли фиксировать конечную границу для числа элементарных шагов?

Следует ли фиксировать конечную границу для размера памяти?

Следует ли ограничить число шагов вычисления?

Таким образом, уточнение понятия алгоритма связано с уточнением алфавита данных и формы их представления, памяти и размещения в ней данных, элементарных шагов алгоритма и механизма реализации алгоритма. Однако эти понятия сами нуждаются в уточнении. Ясно, что их словесные определения потребуют введения новых понятий, для которых, в свою очередь, снова потребуются уточнения и т.д. Поэтому в теории алгоритмов принят другой подход, основанный на конкретной алгоритмической модели, в которой все сформулированные требования выполняются очевидным образом. При этом используемые алгоритмические модели универсальны, то есть моделируют любые другие разумные алгоритмические модели, что позволяет снять возможное возражение против такого подхода: не приводит ли жесткая фиксация алгоритмической модели к потере общности формализации алгоритма? Поэтому данные алгоритмические модели отождествляются с формальным понятием алгоритма.

Всякому алгоритму соответствует задача, для решения которой он был построен. Обратное утверждение в общем случае является неверным по двум причинам: во-первых, одна и та же задача может решаться различными алгоритмами; во-вторых, можно предположить (пока), что имеются задачи, для которых алгоритм вообще не может быть построен.

Интерес математиков к задачам подобного рода привел к постановке вопроса: возможно ли, не решая задачи, доказать, что она алгоритмически неразрешима, т.е. что нельзя построить алгоритм, который обеспечил бы ее общее решение? Ответ на этот вопрос важен, в том числе и с практической точки зрения, например, бессмысленно пытаться решать задачу на компьютере и разрабатывать для нее программу, если доказано, что она алгоритмически неразрешима. Именно для ответа на данный вопрос и понадобилось сначала дать строгое определение алгоритма, без чего обсуждение его существования просто не имело смысла. Построение такого определения, как мы знаем, привело к появлению формальных алгоритмических систем, что дало возможность математического доказательства неразрешимости ряда проблем. Оно сводится к доказательству невозможности построения рекурсивной функции, решающей задачу, либо к невозможности построения машины Тьюринга для нее, либо несостоятельности любой другой модели. То есть задача считается алгоритмически неразрешимой, если не существует машины Тьюринга (или рекурсивной функции, или нормального алгоритма Маркова), которая ее решает.

Первые доказательства алгоритмической неразрешимости касались некоторых вопросов логики и самой теории алгоритмов. Оказалось, например, что неразрешима задача установления истинности произвольной формулы исчисления предикатов – эта теорема была доказана в 1936 г. Чёрчем.

В 1946-47 гг. А.А. Марков и Э. Пост независимо друг от друга доказали отсутствие алгоритма для распознавания эквивалентности слов в любом ассоциативном исчислении.

Важность доказательства алгоритмической неразрешимости в том, что если такое доказательство получено, оно имеет смысл закона-запрета, позволяющего не тратить усилия на поиск решения, подобно тому, как законы сохранения в физике делают бессмысленными попытки построения вечного двигателя. Вместе с этим необходимо сознавать, что алгоритмическая неразрешимость какой-либо задачи в общей постановке не исключает возможности того, что разрешимы какие-то её частные случаи. Справедливо и обратное утверждение: решение частного случая задачи еще не дает повода считать возможным её решения в самом общем случае, т.е. не свидетельствует об ее общей алгоритмической разрешимости.

Роль абстрактных алгоритмических систем в том, что именно они позволяют оценить возможность нахождения общего решения некоторого класса задач. Для специалиста в области информатики важно сознавать, что наличие алгоритмически неразрешимых проблем приводит к тому, что оказывается невозможным построить универсальный алгоритм, пригодный для решения любой задачи. К подобным проблемам приводят и попытки алгоритмизировать сложную интеллектуальную деятельность человека, например, обучение других людей, сочинение стихов и пр.

2. Алгоритм как абстрактная машина

Этот тезис дает алгоритмическое истолкование понятия частично рекурсивной функции. Его нельзя доказать, поскольку он связывает нестрогое математическое понятие интуитивно вычислимой функции со строгим математическим понятием частично рекурсивной функции. Однако исследования, проводившиеся весьма многими математиками в течение нескольких десятилетий, выявили полную целесообразность считать понятие частично рекурсивной функции научным эквивалентом интуитивного понятия вычислимой частичной функции.

Тезис Чёрча оказался достаточным, чтобы придать необходимую точность формулировкам алгоритмических проблем и в ряде случаев сделать возможным доказательство их неразрешимости. Причина заключается в том, что обычно в алгоритмических проблемах математики речь идет не об алгоритмах, а о вычислимости некоторых специальным образом построенных функций. В силу тезиса Чёрча вопрос о вычислимости функции равносилен вопросу о ее рекурсивности. Понятие рекурсивной функции строгое. Поэтому обычная математическая техника позволяет иногда непосредственно доказать, что решающая задачу функция не может быть рекурсивной. Именно этим путем самому Чёрчу удалось доказать неразрешимость основной алгоритмической проблемы логики предикатов – проблемы тождественной истинности формул исчисления первой ступени.

Точное описание класса частично рекурсивных функций вместе с тезисом Чёрча дает одно из возможных решений задачи об уточнении понятия алгоритма. Однако это решение не вполне прямое, так как понятие вычислимой функции является вторичным по отношению к понятию алгоритма. Спрашивается, нельзя ли уточнить непосредственно само понятие алгоритма и уже затем при его помощи определить точно и класс вычислимых функций? Такое направление поиска привело к построению иного, нежели рекурсивные функции, класса моделей алгоритма. Основная его идея состоит в том, что алгоритмические процессы – это процессы, которые может осуществлять определенным образом устроенная машина, моделирующая тем самым выполнение отдельных операций человеком. Функционирование такой машины и есть выполнение некоторого алгоритма.

Исходя из свойств алгоритма, можно сформулировать общие требования к таким машинам:

характер их функционирования должен быть дискретным, т.е. состоять из отдельных шагов (команд), каждый из которых выполняется только после завершения предыдущего;

действия должны быть детерминированы, т.е. шаги выполняются в строгом порядке, а их результат определяется самим шагом и результатами предыдущих шагов;

перед началом работы машине предоставляются исходные данные из области определения алгоритма;

за конечное число шагов работы машины должен быть получен результат или информация о том, что считать результатом;

машина должна быть универсальной, т.е. такой, чтобы с её помощью можно было бы выполнить любой алгоритм.

Пусть исходные данные из области определения алгоритма представлены посредством алфавита A и образуют при этом конечную последовательность знаков – такая последовательность называется словом. В результате выполнения алгоритма сформируется новое слово , представленное, в общем случае, в другом алфавите B. На первый взгляд для проведения такого преобразования в качестве элементарных выделяются следующие операции (шаги):

замена одного знака исходного слова a i знаком b j из алфавита B;

удаление знака исходного слова;

добавление к исходному слову знака из алфавита B.

Однако если в алфавиты включен знак, имеющий смысл пустого знака, добавление которого к слову слева или справа не изменяет этого слова, по аналогии добавления слева числового нуля к числу, то легко видеть, что: операция (2) есть ни что иное, как замена a i пустым знаком, а операция (3) есть замена пустого знака знаком b j . Таким образом, все возможные алфавитные преобразования сводятся к операции (1) – замене одного знака другим. Именно по этой причине функционирование абстрактной машины сводится к тому, что она считывает и распознает символы, записанные в памяти, в качестве которой выступает бесконечная лента, и, в зависимости от своего состояния, и того, каков обозреваемый символ, она заменяет его другим символом. После этого она переходит в новое состояние, читает следующий символ и т.д. до команды о прекращении работы. Поскольку подобные машины являются чисто модельным, теоретическим построением, они получили название абстрактных машин и рассматриваются в качестве одной из возможных универсальных алгоритмических систем.

3. Алгоритмическая машина Поста

x – номер исполняемой команды;

K – указание о выполняемом действии;

y – номер следующей команды (наследника).

Система команд машины, включающая шесть действий, представлена в таблице 1.

Машина Тьюринга - одно из самых интригующих и захватывающих интеллектуальных открытий 20-го века. Это простая и полезная абстрактная модель вычислений (компьютерных и цифровых), которая является достаточно общей для воплощения любой компьютерной задачи. Благодаря простому описанию и проведению математического анализа она образует фундамент теоретической информатики. Это исследование привело к более глубокому познанию цифровых компьютеров и исчислений, включая понимание того, что существуют некоторые вычислительные проблемы, не решаемые на общих пользовательских ЭВМ.

Что это и кто создал

Алан Тьюринг стремился описать наиболее примитивную модель механического устройства, которая имела бы те же основные возможности, что и компьютер. Тьюринг впервые описал машину в 1936 году в статье "О вычислимых числах с приложением к проблеме разрешимости", которая появилась в Трудах Лондонского математического общества.

Из чего состоит устройство

Каждая такая машина состоит из двух составляющих:

Неограниченная лента. Она является бесконечной в обе стороны и разделена на ячейки.
Автомат – управляемая программа, головка-сканер для считывания и записи данных. Она может находиться в каждый момент в одном из множества состояний.

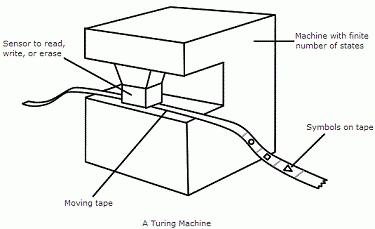
Как работает механизм

Машина Тьюринга имеет принципиальное отличие от вычислительных устройств – ее запоминающее приспособление имеет бесконечную ленту, тогда как у цифровых аппаратов такое устройство имеет полосу определенной длины. Каждый класс заданий решает только одна построенная машина Тьюринга. Задачи иного вида предполагают написание нового алгоритма.

Управляющее устройство, находясь в одном состоянии, может передвигаться в любую сторону по ленте. Оно записывает в ячейки и считывает с них символы конечного алфавита. В процессе перемещения выделяется пустой элемент, который заполняет позиции, не содержащие входные данные. Алгоритм для машины Тьюринга определяет правила перехода для управляющего устройства. Они задают головке записи-чтения такие параметры: запись в ячейку нового символа, переход в новое состояние, перемещение влево или вправо по ленте.

Свойства механизма

Машина Тьюринга, как и другие вычислительные системы, имеет присущие ей особенности, и они сходны со свойствами алгоритмов:

Дискретность. Цифровая машина переходит к следующему шагу n+1 только после того, как будет выполнен предыдущий. Каждый выполненный этап назначает, каким будет n+1.
Понятность. Устройство выполняет только одно действие для одной же ячейки. Оно вписывает символ из алфавита и делает одно движение: влево или вправо.
Детерминированность. Каждой позиции в механизме соответствует единственный вариант выполнения заданной схемы, и на каждом этапе действия и последовательность их выполнения однозначны.
Результативность. Точный результат для каждого этапа определяет машина Тьюринга. Программа выполняет алгоритм и за конечное число шагов переходит в состояние q0.
Массовость. Каждое устройство определено над допустимыми словами, входящими в алфавит.

Функции машины Тьюринга

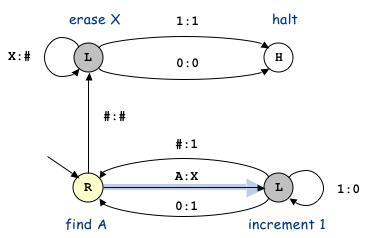
Программа для устройства

Программы для механизма Тьюринга оформляются таблицами, в которых первые строка и столбец содержат символы внешнего алфавита и значения возможных внутренних состояний автомата - внутренний алфавит. Табличные данные являются командами, которые воспринимает машина Тьюринга. Решение задач происходит таким образом: буква, считываемая головкой в ячейке, над которой она в данный момент находится, и внутреннее состояние головки автомата обусловливают, какую из команд необходимо выполнять. Конкретно такая команда находится на пересечении символов внешнего алфавита и внутреннего, находящихся в таблице.

Составляющие для вычислений

Чтобы построить машину Тьюринга для решения одной определенной задачи, необходимо определить для нее следующие параметры.

Внешний алфавит. Это некоторое конечное множество символов, обозначающихся знаком А, составляющие элементы которого именуются буквами. Один из них - а0 - должен быть пустым. Для примера, алфавит устройства Тьюринга, работающего с двоичными числами, выглядит так: A = .

Непрерывная цепочка букв-символов, записываемая на ленту, именуется словом.

Автоматом называется устройство, которое работает без вмешательства людей. В машине Тьюринга он имеет для решения задач несколько различных состояний и при определенно возникающих условиях перемещается из одного положения в другое. Совокупность таких состояний каретки есть внутренний алфавит. Он имеет буквенное обозначение вида Q=. Одно из таких положений - q1 - должно являться начальным, то есть тем, что запускает программу. Еще одним необходимым элементом является состояние q0, которое является конечным, то есть тем, что завершает программу и переводит устройство в позицию остановки.

Таблица переходов. Эта составляющая представляет собой алгоритм поведения каретки устройства в зависимости от того, каковы в данный момент состояние автомата и значение считываемого символа.

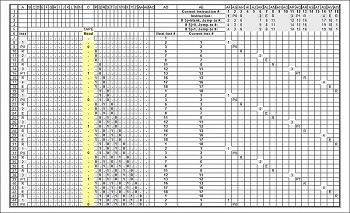
Алгоритм для автомата

Кареткой устройства Тьюринга во время работы управляет программа, которая во время каждого шага выполняет последовательность следующих действий:

Запись символа внешнего алфавита в позицию, в том числе и пустого, осуществляя замену находившегося в ней, в том числе и пустого, элемента.
Перемещение на один шаг-ячейку влево или же вправо.
Изменение своего внутреннего состояния.

Таким образом, при написании программ для каждой пары символов либо положений необходимо точно описать три параметра: a_i – элемент из выбранного алфавита A, направление сдвига каретки ("←” влево, "→” вправо, "точка” — отсутствие перемещения) и q_k - новое состояние устройства. К примеру, команда 1 "←” q₂ имеет значение "заместить символ на 1, сдвинуть головку каретки влево на один шаг-ячейку и сделать переход в состояние q₂”.

Машина Тьюринга: примеры

Решение. В случае если последняя цифра равняется 9, то ее нужно заменить на 0 и затем прибавить единицу к предшествующему символу. Программа в этом случае для данного устройства Тьюринга может быть написана так:

a₀	0	1	2	3	.	7	8	9
q₁	1 H q₀	1 H q₀	2 H q₀	3 H q₀	4 H q₀	.	8 H q₀	9 H q₀	0 λ q₁

Здесь q₁ — состояние изменения цифры, q₀ — остановка. Если в q₁ автомат фиксирует элемент из ряда 0..8, то он замещает ее на один из 1..9 соответственно и затем переключается в состояние q₀, то есть устройство останавливается. В случае если же каретка фиксирует число 9, то замещает ее на 0, затем перемещается влево, останавливаясь в состоянии q₁. Такое движение продолжается до того момента, пока устройство не зафиксирует цифру, меньшую 9. Если все символы оказались равными 9, они замещаются нулями, на месте старшего элемента запишется 0, каретка переместится влево и запишет 1 в пустую клетку. Следующим шагом будет переход в состояние q₀ – остановка.

Пример 2. Дан ряд из символов, обозначающих открывающие и закрывающие скобки. Требуется построить устройство Тьюринга, которое выполняло бы удаление пары взаимных скобок, то есть элементов, расположенных подряд – “( )”. Например, исходные данные: “) ( ( ) ( ( )”, ответ должен быть таким: “) . . . ( (”. Решение: механизм, находясь в q₁, анализирует крайний слева элемент в строке.

a₀	(	)
q₁	a₀ H q₀	( П q₂	) П q₁
q₂	a₀ H q₀	( П q₂	) λ q₃
q₃	a₀ H q₀	a₀ П q₃	a₀ П q1

Состояние q₁: если встречен символ “(”, то совершить сдвиг вправо и переход в положение q₂; если определен “a₀”, то остановка.

Состояние q₂: проводится анализ скобки “(” на наличие парности, в случае совпадения должно получиться “)”. Если элемент парный, то сделать возврат каретки влево и перейти в q₃.

Состояние q₃: осуществить удаление сначала символа “(”, а затем “)” и перейти в q₁.

ГОСТ

Машина Тьюринга — это абстрактный исполнитель или абстрактная вычислительная машина.

Введение

Машина Тьюринга является одним из наиболее выдающихся научных изобретений двадцатого века. Она представляла несложную и удобную абстрактную модель вычислительного процесса, которая представлена в обобщённом формате и позволяет реализовать практически все компьютерные задачи. Простое описание и выполненный математический анализ позволяют считать её фундаментом теоретической информатики.

Эта научная работа послужила стимулом к более углублённому изучению цифрового исчисления и компьютерных устройств, в том числе осознание мысли, что есть проблематика в сфере вычислений, которую нельзя решить на обычных электронных вычислительных машинах пользователей

Машина Тьюринга

Машина Тьюринга была вычислительным модулем, который состоит из сканера для чтения и записи информации с бумажной ленты, пропускаемой через него. Лента поделена на квадратики, несущие один знак, а именно нуль или единицу. Механизм предназначен для ввода и вывода информации и одновременно служит рабочей памятью для сохранения итогов промежуточных вычислительных шагов. Машина имеет в своём составе два компонента:

Лента без ограничений, то есть бесконечная в обоих направлениях лента, разделённая на комплект ячеек.
Автоматический модуль, то есть головка сканера, которая считывает и записывает информацию под управлением программы. Она способна располагаться в любой момент времени лишь в одном из многих состояний.

Готовые работы на аналогичную тему

Машина осуществляет связь двух конечных рядов информационных данных, а именно алфавит знаков на входе $A = (a_0, a_1, …, a_m)$ и алфавит состояний $Q = (q_0, q_1, . q_p)$. Пассивным считается состояние $q_0$. Предполагается, что машина прекращает выполнение операций, когда считывает именно его. Исходным состоянием является состояние $q_1$, и устройство запускается в работу, когда считывает это стартовое состояние. Слово на ленте, которое является входной информацией, расположено последовательно по одной букве в позиции. При этом, впереди него и за ним расположены нулевые квадраты.

Принцип работы машины Тьюринга

Машина Тьюринга принципиально отличается от компьютерных модулей, у неё в качестве запоминающего устройства выступает бесконечная лента, а у цифровых устройств память представляет полосу заданной длины. Любой тип заданий может решить лишь одна сформированная машина Тьюринга. Задания другого класса могут быть решены написанием другого алгоритма. Устройство управления находится в определённом состоянии и способно перемещаться в обе стороны вдоль ленты. Оно может записывать в ячейки и считывать из них алфавитные символы. При перемещении определяется пустой компонент, заполняющий места, которые не содержать входных данных. Алгоритм машины Тьюринга формирует условия перемещений управляющего механизма. Он может задать головке, выполняющей запись и чтение данных, следующие команды:

Записать в текущую ячейку нужный знак.
Выполнить смену текущего состояния.
Переместиться в заданную сторону вдоль ленты.

Машина Тьюринга подобно другим системам, предназначенным для вычислений, обладает определёнными особенностями, которые похожи на свойства алгоритмов:

Свойство дискретности. Цифровое устройство выполняет переход к очередному этапу n+1 лишь после полного завершения предыдущего. Каждый завершенный шаг определяет, каким будет следующий.
Свойство понятности. Машина осуществляет лишь одну операцию для выбранной ячейки. Она записывает алфавитный символ и выполняет одно перемещение в указанную сторону.
Свойство детерминированности. Всем позициям в машине сопоставляется только один вариант осуществления задаваемой схемы, и на всех шагах операции и их очерёдность осуществления строго определены.
Свойство результативности. Окончательный итог на каждом шаге вычисляет машина Тьюринга. Программа работает согласно заданному алгоритму и за не бесконечное количество выполненных этапов доходит до состояния $q_0$.
Свойство массовости. Каждой машине сопоставлен набор допустимых слов, которые входят в алфавит.

Функции машины Тьюринга

Рисунок 1. Функции машины Тьюринга. Автор24 — интернет-биржа студенческих работ

Программа для машины Тьюринга

Программа для машины Тьюринга формируется как таблицы, в которых в первой строчке и столбце находятся знаки внешнего алфавита и набор допустимых внутренних состояний автомата, то есть внутренний алфавит. Данные в таблице, по сути, это команды, которые должна исполнять машина Тьюринга. Разрешение задачи выполняется по следующим правилам. Символ, принятый сканером из ячейки, над которой он располагается в текущий момент, и определённое внутреннее состояние сканера автомата определяют, какую команду требуется исполнить. А именно, это команда, расположенная в таблице, и находящаяся в точке пересечения знаков внутреннего и внешнего алфавита.

Варианты словесного определения алгоритма принадлежат российским ученым А.Н. Колмогорову и А.А. Маркову.

− алгоритм должен содержать конечное количество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;

− алгоритм должен выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;

− алгоритм должен быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;

− алгоритм должен приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.

1. Каждый алгоритм имеет дело с данными – входными, промежуточными, выходными. Для того чтобы уточнить понятие данных, фиксируется конечный алфавит исходных символов (цифры, буквы и т.п.) и указываются правила построения алгоритмических объектов. Типичным используемым средством является индуктивное построение. Например, определение идентификатора во многих алгоритмических языках: идентификатор – это либо буква, либо идентификатор, к которому приписана справа либо буква, либо цифра. Слова конечной длины в конечных алфавитах – наиболее обычный тип алгоритмических данных, а число символов в слове – естественная мера объема данных. Другой случай алгоритмических объектов – формулы. Примером могут служить формулы алгебры предикатов и алгебры высказываний.

2. Алгоритм для размещения данных требует памяти. Память обычно считается однородной и дискретной, т.е. она состоит из одинаковых ячеек, причем каждая ячейка может содержать один символ данных, что позволяет согласовать единицы измерения объема данных и памяти.

3. Алгоритм состоит из отдельных элементарных шагов, причем множество различных шагов, из которых составлен алгоритм, конечно. Типичный пример множества элементарных шагов – система команд ЭВМ.

4. Последовательность шагов алгоритма детерминирована, то есть после каждого шага указывается, какой шаг следует выполнять дальше, либо указывается, когда следует работу алгоритма считать законченной.

5. Алгоритм должен обладать результативностью, то есть останавливаться после конечного числа шагов (зависящего от исходных данных) с выдачей результата. Данное свойство иногда называют сходимостью алгоритма.

6. Алгоритм предполагает наличие механизма реализации, который по описанию алгоритма порождает процесс вычисления на основе исходных данных. Предполагается, что описание алгоритма и механизм его реализации конечны.

1. Следует ли фиксировать конечную границу для размера входных данных?

2. Следует ли фиксировать конечную границу для числа элементарных шагов?

3. Следует ли фиксировать конечную границу для размера памяти?

4. Следует ли ограничить число шагов вычисления?

2. Алгоритм как абстрактная машина

Исходя из свойств алгоритма, можно сформулировать общие требования к таким машинам:

1. характер их функционирования должен быть дискретным, т.е. состоять из отдельных шагов (команд), каждый из которых выполняется только после завершения предыдущего;

2. действия должны быть детерминированы, т.е. шаги выполняются в строгом порядке, а их результат определяется самим шагом и результатами предыдущих шагов;

3. перед началом работы машине предоставляются исходные данные из области определения алгоритма;

4. за конечное число шагов работы машины должен быть получен результат или информация о том, что считать результатом;

5. машина должна быть универсальной, т.е. такой, чтобы с её помощью можно было бы выполнить любой алгоритм.

Пусть исходные данные из области определения алгоритма представлены посредством алфавита A и образуют при этом конечную последовательность знаков 1…a_n> – такая последовательность называется словом. В результате выполнения алгоритма сформируется новое слово 1…b_m>, представленное, в общем случае, в другом алфавите B. На первый взгляд для проведения такого преобразования в качестве элементарных выделяются следующие операции (шаги):

1. замена одного знака исходного слова a_i знаком b_j из алфавита B;

Читайте также: