Непрерывное сообщение как вы это понимаете

Обновлено: 17.05.2024

Передача информации производится с помощью сигналов, а самим сигналом является изменение некоторой характеристики носителя с течением времени. При этом в зависимости от особенностей изменения этой характеристики (т.е. параметра сигнала) с течением времени выделяют два типа сигналов: непрерывные и дискретные .

Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала

Если обозначить Z- значение параметра сигнала, at- время, то зависимость Z(t) будет непрерывной функцией (рис.1.2,а).

Рис. 1.2. Непрерывные (а) и дискретные (б) сигналы

Примерами непрерывных сигналов являются речь и музыка, изображение, показание термометра (параметр сигнала - высота столба спирта или ртути - имеет непрерывный ряд значений) и пр.

Сигнал называется дискретным, если его параметр может принимать конечное число значений в пределах некоторого интервала.

Пример дискретных сигналов представлен на рис. 1.2,б. Как следует из определения, дискретные сигналы могут быть описаны дискретным и конечным множеством значений параметров . Примерами устройств, использующих дискретные сигналы, являются часы (электронные и механические), цифровые измерительные приборы, книги, табло и пр.

Принципиальным и важнейшим различием непрерывных и дискретных сигналов является то, что дискретные сигналы можно обозначить, т.е. приписать каждому из конечного чисел возможные значения сигнала знак, который будет отличать данный сигнал от другого.

Знак - это элемент некоторого конечного множества отличных друг от друга сущностей.

Вся совокупность знаков, используемых для представления дискретной информации, называется набором знаков.

Таким образом, набор есть дискретное множество знаков.

Набор знаков, в котором установлен порядок их следования, называется алфавитом.

Знаки, используемые для обозначения фонем человеческого языка, называются буквами, а их совокупность - алфавитом языка.

Рис. 1.3. Варианты преобразований

Рассмотрим общий подход к преобразованию типа N → D. С математической точки зрения перевод сигнала из аналоговой формы в дискретную означает замену описывающей его непрерывной функции времени Z(t) на некотором отрезке [t₁, t₂] конечным множеством (массивом) i, t_i> (i = 0. n, где n - количество точек разбиения временного интервала). Подобное преобразование называется дискретизацией непрерывного сигнала и осуществляется посредством двух операций: развертки по времени и квантования по величине сигнала.

Развертка по времени состоит в том, что наблюдение за значением величины Z производится не непрерывно, а лишь в определенные моменты времени с интервалом Δt:

Квантование по величине - это отображение вещественных значений параметра сигнала в конечное множество чисел, кратных некоторой постоянной величине - шагу квантования (ΔZ).

Рис. 1.4. Дискретизация аналогового сигнала за счет операций развертки по времени и квантования по величине

При такой замене довольно очевидно, что чем меньше n (больше Δt, тем меньше число узлов, но и точность замены Z(t) значениями Z_i, будет меньшей. Другими словами, при дискретизации может происходить потеря части информации, связанной с особенностями функции Z(t). На первый взгляд кажется, что увеличением количества точек n можно улучшить соответствие между получаемым массивом и исходной функцией, однако полностью избежать потерь информации все равно не удастся, поскольку n - величина конечная.

Ответом на эти сомнения служит так называемая теорема отсчетов, доказанная в 1933г. В. А. Котельниковым (по этой причине ее иногда называют его именем), значение которой для решения проблем передачи информации было осознано лишь в 1948г. после работ К. Шеннона. Теорема, которую примем без доказательства, но результаты будем в дальнейшем использовать, гласит:

Непрерывный сигнал можно полностью отобразить и точно воссоздать по последовательности измерений или отсчетов величины этого сигнала через одинаковые интервалы времени, меньшие или равные половине периода максимальной частоты, имеющейся в сигнале.

Комментарии к теореме:

Теорема касается только тех линий связи, в которых для передачи используются колебательные или волновые процессы.

Любое подобное устройство использует не весь спектр частот колебаний, а лишь какую-то его часть; например, в телефонных линиях используются колебания с частотами от 300 Гц до 3400 Гц. Согласно теореме отсчетов определяющим является значение верхней границы частоты - обозначим его V_m.

Смысл теоремы в том, что дискретизация не приведет к потере информации и по дискретным сигналам можно будет полностью восстановить исходный аналоговый сигнал, если развертка по времени выполнена в соответствии со следующим соотношением:

Можно перефразировать теорему отсчетов:

Развертка по времени может быть осуществлена без потери информации, связанной с особенностями непрерывного (аналогового) сигнала, если шаг развертки не будет превышать Δt, определяемый в соответствии с (1.2).

Например, для точной передачи речевого сигнала с частотой до V_m = 4000 Гц при дискретной записи должно производиться не менее 8000 отсчетов в секунду; в телевизионном сигнале V_m ≈ 4 МГц, следовательно, для его точной передачи потребуется около 8000000 отсчетов в секунду.

Однако, помимо временной развертки, дискретизация имеет и другую составляющую - квантование. Выясним, как определяется шаг квантования ΔZ?

Таким образом, преобразование сигналов типа N → D, как и обратное D → N, может осуществляться без потери, содержащейся в них информации.

Преобразование типа D₁ → D₂ состоит в переходе при представлении сигналов от одного алфавита к другому - такая операция носит название перекодировка и может осуществляться без потерь. Примерами ситуаций, в которых осуществляются подобные преобразования, могут быть: запись-считывание с компьютерных носителей информации; шифровка и дешифровка текста; вычисления на калькуляторе.

• простоту и, как следствие, надежность и относительную дешевизну устройств по обработке информации;

• точность обработки информации, которая определяется количеством обрабатывающих элементов и не зависит от точности их изготовления;

Информация, порождаемая и существующая в природе, связана с материальным миром - это размеры, форма, цвет и другие физические, химические и прочие характеристики и свойства объектов. Данная информация передается посредством физических и иных взаимодействий и процессов. Эту природную информацию можно считать хаотической и неупорядоченной, поскольку никем и ничем не регулируется ее появление, существование, использование. Чаще всего она непрерывна по форме представления. Напротив, дискретная информация - это информация, прошедшая обработку - отбор, упорядочение, преобразование; она предназначена для дальнейшего применения человеком или техническим устройством. Другими словами, дискретная - это уже частично осмысленная информация, т.е. имеющая для кого-то смысл и значение и, как следствие, более высокий (с точки зрения пользы) статус, нежели непрерывная.

вероятность появления отдельной реализации равна нулю. Если попытаться определить энтропию и производительность такого источника путем предельного перехода, как это было сделано и § 2.10 для непрерывных сигналов, то они окажутся бесконечными. Однако это не означает, что информация, интересующая получателя и подлежащая передаче по каналу, также бесконечна.

Очевидно, количество информации зависит не только от статистики процесса определяющей дифференциальную

Подставив сюда (6.6), получим для гауссовского источника с равномерным спектром в полосе

Из предыдущих рассуждений ясно, что производительность гауссовского источника квазибелого шума (6.9) больше производительности любого другого источника с той же мощностью и той же шириной спектра при том же допустимом шуме воспроизведения Количество информации, выдаваемое гауссовским источником за время

Выражение (6.10) совпадает с характеристикой (1.1), названной в § 1.1 объемом сигнала, если Это означает, что объем сигнала равен максимальному количеству информации, которая содержится в сигнале длительностью

Для непрерывного канала с пропускной способностью С, на вход которого подключен источник, обладающий производительностью К. Шеннон доказал следующую теорему.

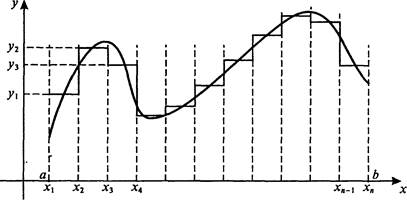
Ось значений функции можно разбить на отрезки с заданным шагом и отобразить каждый из выделенных отрезков из области определения функции в соответствующий отрезок из множества значений (рис. 1.4). В итоге получим конечное множество чисел, определяемых, например, по середине или одной из границ таких отрезков.

Возможность дискретизации непрерывного сигнала с любой желаемой точностью (для возрастания точности достаточно уменьшить шаг) принципиально важна с точки зрения информатики. Компьютер - цифровая машина, т. е- внутреннее представление информации в нем дискретно. Дискретизация входной информации (если она непрерывна) позволяет сделать ее пригодной для компьютерной обработки.

2.3. ЕДИНИЦЫ КОЛИЧЕСТВА ИНФОРМАЦИИ:
ВЕРОЯТНОСТНЫЙ И ОБЪЕМНЫЙ ПОДХОДЫ

Вероятностный подход

Рассмотрим в качестве примера опыт, связанный с бросанием правильной игральной .кости, имеющей N граней (наиболее распространенным является случай шестигранной кости: N = 6). Результаты данного опыта могут быть следующие: выпадение грани с одним из следующих знаков: 1,2. N.

Введем в рассмотрение численную величину, измеряющую неопределенность -энтропию (обозначим ее Н). Величины N и Н связаны между собой некоторой функциональной зависимостью:

а сама функция f является возрастающей, неотрицательной и определенной (в рассматриваемом нами примере) для N = 1, 2. 6.

Рассмотрим процедуру бросания кости более подробно:

1) готовимся бросить кость; исход опыта неизвестен, т.е. имеется некоторая неопределенность; обозначим ее H1;

2) кость брошена; информация об исходе данного опыта получена; обозначим количество этой информации через I;

I = H1 - H2 (1.2)

Следующим важным моментом является определение вида функции f в формуле (1.1). Если варьировать число граней N и число бросаний кости (обозначим эту величину через М), общее число исходов (векторов длины М, состоящих из знаков 1,2. N) будет равно N в степени М:

Так, в случае двух бросаний кости с шестью гранями имеем: Х = 6 2 = 36. Фактически каждый исход Х есть некоторая пара (X1, X2), где X1 и X2 - соответственно исходы первого и второго бросаний (общее число таких пар - X).

f(6 M ) = M ∙ f(6)

Данную формулу можно распространить и на случай любого N:

F(N M ) = M ∙ f(N) (1.4)

Прологарифмируем левую и правую части формулы (1.3): ln X = M ∙ ln N, М =ln X/1n M. Подставляем полученное для M значение в формулу (1.4):

Обозначив через К положительную константу , получим: f(X) = К ∙ lп Х, или, с учетом (1.1), H=K ∙ ln N. Обычно принимают К = 1 / ln 2. Таким образом

H = log₂ N. (1.5)

Это - формула Хартли.

Та же формула (1.6) принимается за меру энтропии в случае, когда вероятности различных исходов опытанеравновероятны (т.е. Р_i могут быть различны). Формула (1.6) называетсяформулой Шеннона.

Н = log₂ 34 ≈ 5 бит.

Однако, в словах русского языка (равно как и в словах других языков) различные буквы встречаются неодинаково часто. Ниже приведена табл. 1.3 вероятностей частоты употребления различных знаков русского алфавита, полученная на основе анализа очень больших по объему текстов.

Воспользуемся для подсчета Н формулой (1.6); Н ≈ 4,72 бит. Полученное значение Н, как и можно было предположить, меньше вычисленного ранее. Величина Н, вычисляемая по формуле (1.5), является максимальным количеством информации, которое могло бы приходиться на один знак.

Таблица 1.3. Частотность букв русского языка

i	Символ	Р(i)	i	Символ	P(i)	i	Символ	Р(i)
Пробел	0,175	0,028	Г	0.012
0,090	М	0,026	Ч	0,012
Е	0,072	Д	0,025	И	0,010
Ё	0,072	П	0,023	X	0,009
А	0,062	У	0,021	Ж	0,007
И	0,062	Я	0,018	Ю	0,006
Т	0,053	Ы	0,016	Ш	0.006
Н	0,053	З	0.016	Ц	0,004
С	0,045	Ь	0,014	Щ	0,003
Р	0,040	Ъ	0,014	Э	0,003
В	0,038	Б	0,014	Ф	0,002
Л	0,035

H = log₂ 27 ≈ 4,76 бит.

Как и в случае русского языка, частота появления тех или иных знаков не одинакова.

Если расположить все буквы данных языков в порядке убывания вероятностей, то получим следующие последовательности:

Рассмотрим алфавит, состоящий из двух знаков 0 и 1. Если считать, что со знаками 0 и 1 в двоичном алфавите связаны одинаковые вероятности их появления (Р(0) = Р(1) = 0,5), то количество информации на один знак при двоичном кодировании будет равно

H = 1оg₂ 2 = 1 бит.

Таким образом, количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.

Объемный подход

В двоичной системе счисления знаки 0 и 1 будем называть битами (от английского выражения Binary digiTs - двоичные цифры). Отметим, что создатели компьютеров отдают предпочтение именно двоичной системе счисления потому, что в техническом устройстве наиболее просто реализовать два противоположных физических состояния: некоторый физический элемент, имеющий два различных состояния: намагниченность в двух противоположных направлениях; прибор, пропускающий или нет электрический ток; конденсатор, заряженный или незаряженный и т.п. В компьютере бит является наименьшей возможной единицей информации. Объем информации, записанной двоичными знаками в памяти компьютера или на внешнем носителе информации подсчитывается просто по количеству требуемых для такой записи двоичных символов. При этом, в частности, невозможно нецелое число битов (в отличие от вероятностного подхода).

Для удобства использования введены и более крупные, чем бит, единицы количества информации. Так, двоичное слово из восьми знаков содержит один, байт информации, 1024 байта образуют килобайт (кбайт), 1024 килобайта - мегабайт (Мбайт), а 1024 мегабайта - гигабайт (Гбайт).

В дальнейшем тексте данного учебника практически всегда количество информации понимается в объемном смысле.

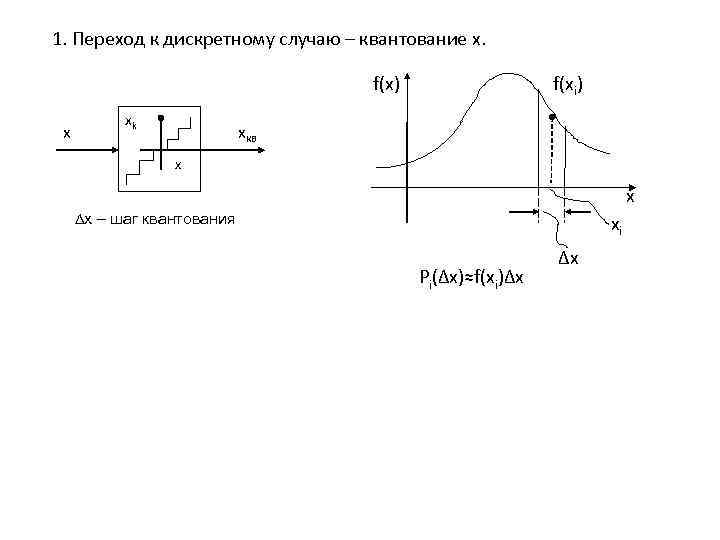
1. Переход к дискретному случаю – квантование x. f(x) f(xi) xk x xкв x x ∆x – шаг квантования xi ∆x Pi(∆x)≈f(xi)∆x

Взаимная информация fx(xi) fy(y) fx(x) fy(yi) ∆x x ∆y y xi yi Дано: Воспоминания: Если x и y статистически не связаны, то Если x и y однозначно связаны:

Средняя взаимная информация.

Максимум дифференциальной энтропии. Задача 1. Определить максимум при заданном диапазоне случайной величины X: а≤x≤в. Таким образом: а≤x≤в; Воспоминания: y(x)-неизвестная функция.

Условие Требуется найти y(x), доставляющую максимум (минимум) J. Уравнение Эйлера:

Решение:

Задача 2. Определить максимум дифференциальной энтропии при заданной мощности (дисперсии) сигнала. Определить максимум при условии: Обратите внимание: диапазон не ограничен (1); математическое ожидание принято равным 0 (2).

Решение: а в

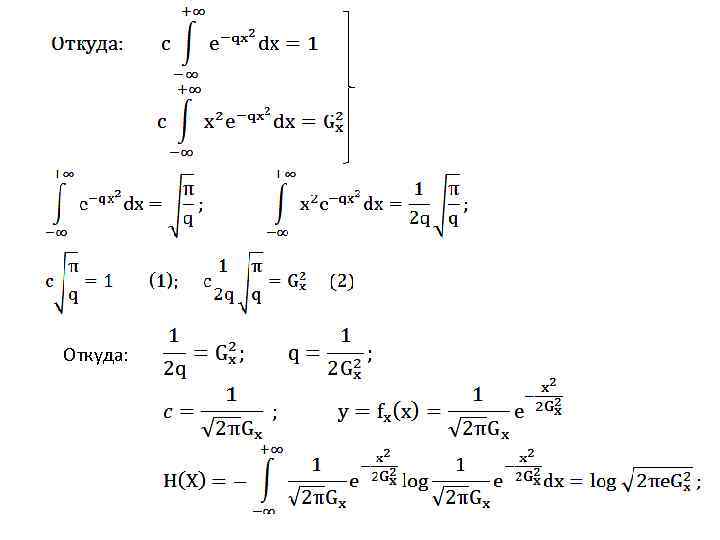
Откуда:

3) В соответствии с теоремой Котельникова передаём информацию с шагом временной дискретизации. Эти отсчеты не коррелированны (а так как сигнал гауссовский, то и независимы). Некоррелированность следует из Отсюда источник отсчетов без памяти. 4) Производительность гауссовского источника при фиксированном Δx (этим учитываем факт использования дифференциальной энтропии) равна: Пропускная способность гауссовского канала связи (формула Шеннона-Таллера).

4. Помеха имеет постоянную спектральную плотность мощности в полосе канала от 0 до Отсюда следует, что отсчеты помехи с шагом временной дискретизации статистически независимы.

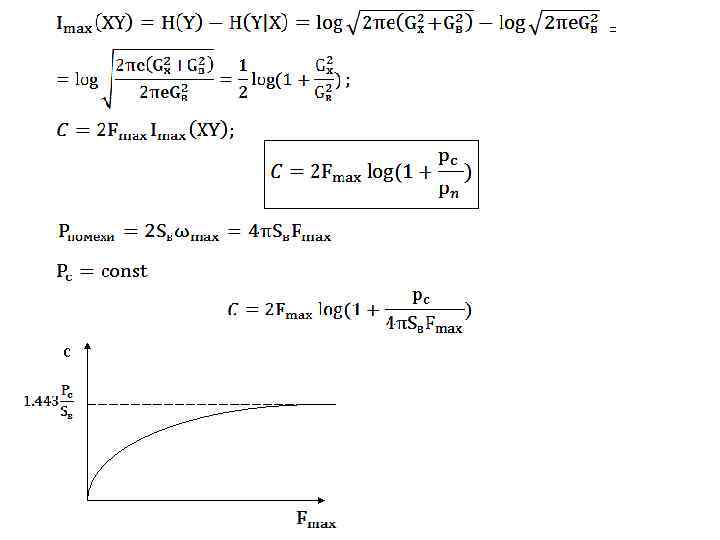
= с

Читайте также: