Движение в пространстве сообщение

Обновлено: 02.07.2024

Движения в пространстве Движение – это преобразование фигуры, при котором расстояния между любыми соответственными точками фигуры сохраняются СВОЙСТВА Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения. При движении прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки При движении сохраняются углы между полупрямыми.

Центральная симметрия. (Симметрия относительно точки) Центральная симметрия – отображение пространства на себя, при котором любая точка А переходит в симметричную ей точку А 1 относительно данного центра О .

Две точки А и В называются симметричными относительно точки О, если О — середина отрезка АВ Точка О считается симметричной самой себе. Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией .

Фигуры обладающие центральной симметрией Примерами фигур, обладающих центром симметрии, являются параллелограмм, окружность Прямоугольный параллелепипед центрально симметричен относительно точки пересечения диагоналей Октаэдр, икосаэдр, додекаэдр имеют несколько осей симметрии Шар центрально симметричен относительно своего центра

Осевая симметрия Симметрия относительно прямой (или осевая симметрия) – это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону прямой, всегда будет соответствовать точка, расположенная по другую сторону прямой, а отрезки, соединяющие эти точки, будут перпендикулярны оси симметрии и делятся ею пополам

Фигуры обладающие осевой симметрией Октаэдр, икосаэдр, додекаэдр имеют несколько осей симметрии Куб имеет 9 плоскостей симметрии Каждая прямая проходящая через центр шара является его осью

Зеркальная симметрия Зеркальной симметрией (симметрией относительно плоскости α ) называется такое отображение пространства на себя, при котором любая точка А переходит в симметричную ей относительно этой плоскости α , точку В

Примеры фигур имеющих зеркальную симметрию Куб имеет 9 плоскостей симметрии Октаэдр, икосаэдр, додекаэдр

Параллельный перенос Параллельным переносом фигуры называется перенос всех точек пространства на одно расстояние в одном направлении.

Поворот Все точки фигуры поворачиваются на один и тот же угол вокруг одной и той же точки – центра поворота.

Симметрию можно встретить в природе

Симметрия в технике

Симметрия в архитектуре и быту

Симметрия в словах и числах. 69

Зеркальная симметрия – это симметрия окружавшего нас мира.

Равенство фигур. Две фигуры называются равными, если они движение переводятся одна в другую.

По теме: методические разработки, презентации и конспекты

Сборник Образовательное пространство - пространство развития

В даннос сборнике содержатся написанные мною статьи за последние три года. Они все опубликованы в разных средствах массовой информации: Учительской газете, газете "Содружество", журналах "Молодой учен.

Тип урока: комбинированный урок с элементами деловой игры Методы обучения: наглядный, словесный, частично-поисковый, с элементами проблемного обучения и деловой игры Цель занятия: расширить область .

РАЗРАБОТКА МЕРОПРИЯТИЙ ПО ОРГАНИЗАЦИИ ДОРОЖНОГО ДВИЖЕНИЯ, ПОВЫШАЮЩИХ БЕЗОПАСНОСТЬ ДОРОЖНОГО ДВИЖЕНИЯ НА АВТОМОБИЛЬНЫХ ДОРОГАХ ФЕДЕРАЛЬНОГО ЗНАЧЕНИЯ

В статье рассматривается решение проблемы дорожно-транспортных происшествий среди пешеходов на автомобильных дорогах федерального значения. Приведена статистика дорожно-транспортных происшествий .

Лекция к разделу "Основы безопасности дорожного движения Вопросы теории движения легкового автомобиля"

Теоретический анализ эксплуатационных свойств помогает выяснить предельные возможности автомобиля и реализовать в дорожных условиях конструктивные особенности конкретной модели автомобиля.К основным э.

Конспект лекций по дисциплине ОП.06 Правила безопасности дорожного движения Раздел №5 Организация работы службы безопасности движения в автотранспортных организациях

Методическая разработка предназначена для студентов СПО специальности 23.02.03 Техническое обслуживание и ремонт автомобильного транспорта. Конспект лекций содержит необходимый теоретический материал .

Пусть каждой точке А пространства поставлена в соответствие точка А₁ пространства. При этом каждая точка А₁ поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А₁.
Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.
Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A₁B₁|.
Центральная симметрия пространства относительно точки O – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O. Точка O – центр симметрии.
Осевая симметрия пространства относительно прямой m – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой . Прямая m – ось симметрии.
Зеркальная симметрия пространства относительно плоскости α – преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α. Плоскость α – плоскость симметрии.
Параллельный перенос на вектор– преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M', что выполняется равенство .
Поворот пространства на угол φ вокруг прямой n – преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.

Основная литература:

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни – М. : Просвещение, 2014. – 255, сс. 121-126.

Дополнительная литература:

Потоскуев Е.В., Звавич Л. И., Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-63.

Открытые электронные ресурсы:

Теоретический материал для самостоятельного изучения

1. Определение движения в пространстве

Допустим, что каждой точке А пространства поставлена в соответствие точка А₁ пространства. При этом каждая точка А₁ поставлена в соответствие какой-то точке А. Тогда говорят, что задано отображение пространства на себя. При этом точка А перешла в точку А₁. А₁ - образ точки А.

Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.

Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают.

Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными.

Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М', а преобразование g отображает точку М' на точку M'', то преобразование f°g отображает точку М на точку M'': f°g(М)=g(f(M))=M''.

f°g - композиция преобразований f и g.

Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A₁ и B₁ так, что |AB|=|A₁B₁|.

Иными словами, движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве

- прямые переходят в прямые,

- полупрямые — в полупрямые,

- отрезки — в отрезки,

- сохраняются углы между прямыми.

Новое свойство движения в пространстве: движение переводит плоскости в плоскости.

В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.

Можно доказать, что композиция двух движений пространства есть движение.

2. Виды движений.

Центральная симметрия в пространстве задается и определяется так же, как и на плоскости

Определение:

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки O, называется центральной симметрией пространства относительно точки O. При этом точка O отображается на себя и называется центром симметрии.

Рисунок 1 – Центральная симметрия

На рисунке точка О – центр симметрии, АО=А₁О, ВО=В₁О, СО=С₁О, DО=D₁О (по определению точки, симметричной данной).

Центральная симметрия имеет только одну неподвижную точку – центр симметрии.

Сформулируем некоторые свойства центральной симметрии:

1) Прямая, проходящая через центр симметрии, отображается на себя.

2) Прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.

3) Плоскость, проходящая через центр симметрии, отображается на себя (то есть является неподвижной плоскостью этой центральной симметрии).

4) Плоскость, не проходящая через центр симметрии, отображается на параллельную ей плоскость.

3. Осевая симметрия (симметрия относительно прямой):

Определение:

Точка M' пространства, не лежащая на прямой m, называется симметричной точке М относительно прямой m, если отрезок ММ' перпендикулярен этой прямой и делится ею пополам.

Определение:

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно прямой m, называется осевой симметрией пространства относительно прямой m. Прямая m отображается на себя и называется осью симметрии.

Рисунок 2 – Осевая симметрия

Неподвижные точки осевой симметрии - любая точка прямой m.

Неподвижные прямые осевой симметрии:

1) сама прямая m

2) любая прямая, перпендикулярная прямой m

Неподвижные плоскости осевой симметрии:

1) любая плоскость, проходящая через прямую m

2) любая плоскость, перпендикулярная прямой m.

Зеркальная симметрия (симметрия относительно плоскости):

Определение:

Точка M' пространства, не лежащая на плоскости α, называется симметричной точке М относительно плоскости α, если отрезок ММ' перпендикулярен этой плоскости и делится ею пополам.

Определение:

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости α, называется зеркальной симметрией пространства относительно плоскости α. Плоскость α отображается на себя и называется плоскостью симметрии.

Рисунок 3 – Зеркальная симметрия

Неподвижные точки зеркальной симметрии - любая точка плоскости α.

Неподвижные прямые зеркальной симметрии:

1) любая прямая плоскости α

2) любая прямая, перпендикулярная плоскости α

Неподвижные плоскости зеркальной симметрии:

1) сама плоскость α

2) любая плоскость, перпендикулярная плоскости α.

Параллельный перенос (точки переносятся на данный вектор):

Рисунок 4 – параллельный перенос

Определение

Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M', что выполняется равенство , называется параллельным переносом на вектор .

Перенос на нулевой вектор является тождественным преобразованием.

Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя.

Неподвижных точек параллельный перенос на ненулевой вектор не имеет.

Неподвижными прямыми при параллельном переносе на вектор являются прямые, параллельные этому вектору.

Неподвижными плоскостями при параллельном переносе на вектор являются плоскости, параллельные этому вектору.

Поворот на данный угол вокруг данной оси:

Определение:

Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.

Рисунок 5 – Поворот вокруг прямой

Неподвижными точками являются любая точка оси вращения.

Неподвижной прямой является ось поворота.

Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота.

Поворот вокруг оси на угол 180 0 является осевой симметрией.

Примеры и разбор решения заданий тренировочного модуля

Дан треугольника АВС: А(3,- 2, 4), В (4, 6, 0), С (2, 2, 2)

В какую точку перейдет центр О пересечения медиан данного треугольника при:

Преобразование

Координата образа

Параллельный перенос на вектор (2; -2; 3)

Симметрия относительно начала координат

Симметрия относительно координатной плоскости ZOY

Поворот на угол 180 0 относительно координатной оси OZ

Симметрия относительно плоскости х=2

Найдем точку пересечения медиант данного треугольника.

Найдем координаты точки М - середины отрезка ВС:

М (); М(3; 4; 1)

Так как медианы треугольника пересекаются в одной точке и делятся в отношении 2:1, считая от вершины, то можем найти координаты точки О, зная координаты А и М:

Теперь найдем координаты образа точки О при каждом из преобразований:.

Симметрия относительно начала координат задается уравнениями:

. То есть координаты образа: (-3; -2; -2)

Симметрия относительно координатной плоскости ZOY задается уравнениями:

(ордината и аппликата точки остаются такими же, а абсцисса меняет знак). То есть координаты образа: (-3; 2; 2).

Поворот на угол 180 0 относительно координатной оси OZ означает симметрию относительно координатной оси OZ и задается уравнениями:

(аппликата точки остается такой же, а ордината и абсцисса меняют знак). То есть координаты образа: (-3; -2; 2).

Эта плоскость параллельная плоскости ZOY, поэтому ордината и аппликата точки остаются такими же. Так как абсцисса токи О х_о =3, то расстояние от точки до плоскости α равно 1. Точка, симметричная точке О относительно плоскости α, будет иметь абсциссу, равную х_о’ =1.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Описание презентации по отдельным слайдам:

Движение в пространстве 11 класс

Понятие движения Движение – это отображение пространства на себя, сохраняющее расстояния между точками

Виды движения Центральная симметрия Осевая симметрия Зеркальная симметрия Параллельный перенос

Центральная симметрия Центральная симметрия — отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О.

Центральная симметрия является движением. Обозначим буквой О центр симметрии и введем прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек М (х; у; z) и М1 (х1, у1; z1), симметричных относительно точки О. Если точка М не совпадает с центром О, то О — середина отрезка ММ1. По формулам координат середины отрезка получаем , откуда х1= - х, у1= -у , z1 = - z. Эти формулы верны и в том случае, когда точки M и О совпадают. О

Рассмотрим теперь две точки А(х1; у1; z1) и В(х2; у2; z2)и докажем, что расстояние между симметричными точками А1 и В1 равно АВ. Точки А1 и В1 имеют координаты А1(-х1 ; -у1 ; - z1) и В1(-х2 ;-у2; -z2). По формуле расстояния между двумя точками AB = A1B1

Осевая симметрия Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а.

Осевая симметрия является движением. Для этого введем прямоугольную систему координат Oxyz так, чтобы ось Oz совпала с осью симметрии, и установим связь между координатами двух точек М(х; у; z) и М1(х1, y1; z1), симметричных относительно оси Oz. Если точка М не лежит на оси Oz , то ось Oz: 1) проходит через середину отрезка ММ1 и 2) перпендикулярна к нему. Из первого условия по формулам для координат середины отрезка получаем , откуда х1= -х и у1 = -у. Второе условие означает, что аппликаты точек М и М1 равны: z1= z2. Полученные формулы верны и в том случае, когда точка М лежит на оси Oz.

Рассмотрим теперь любые две точки A(х1; у1; z1) и В(х2; у2; z2) и докажем, что расстояние между симметричными им точками А1 и В1равно АВ. Точки А1 и В1 имеют координаты А1(-х1 ; -у1 ; - z1) и В1(-х2; -у2; z2). По формуле расстояния между двумя точками находим: AB = A1B1

Зеркальная симметрия Зеркальной симметрией (относительно плоскости ) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно плоскости  точку М1.

Зеркальная симметрия является движением. Для этого введем прямоугольную систему координат Oxyz так, чтобы плоскость Оху совпала с плоскостью симметрии, и установим связь между координатами двух точек М(х; у;z) и М1(х1; у1; z1), симметричных относительно плоскости Оху. Если точка М не лежит в плоскости Оху, то эта плоскость: 1) проходит через середину отрезка ММ1 ; 2) перпендикулярна к нему. М К К  МК=М1К1 М1 К1

Из первого условия по формуле координат середины отрезка получаем : , значит z = -z Второе условие означает, что отрезок ММ1 параллелен оси Oz, и, следовательно, х1=х, у1= у. Полученные формулы верны и в том случае, когда точка М лежит в плоскости Оху. М К К  МК=М1К1 М1 К1

Рассмотрим теперь две точки А(x1, у1; z1) и В (х2; у2; z2) и докажем, что расстояние между симмеричными им точками А1 и В1 равно АВ. Точки А1 и В1 имеют координаты А1(х1 ; у1 ; - z1) и В1(х2; у2; -z2). По формуле расстояния между двумя точками находим: AB = A1B1

Фигуры, симметричные относительно плоскости Фигура ( тело) называется симметричной относительно некоторой плоскости, если эта плоскость разбивает фигуру на две равные симметричные части. Сколько плоскостей симметрии имеет куб? Ответы : 2; 4; 5; 6; 9

Симметрия в пирамиде Верно ли высказывание: правильная четырехугольная пирамида имеет четыре плоскости симметрии

Задачи 1. Сколько плоскостей симметрии имеет пирамида, в основании которой лежит прямоугольник, ромб? Какое дополнительное условие должно присутствовать в условии задачи, чтобы ваш ответ был верен?

Зеркальная симметрия в призме 1)Сколько плоскостей симметрии имеет правильная четырехугольная призма? Ответы: а)2 б)4 в)3 г)5 д)12 2)Сколько плоскостей симметрии имеет прямая призма, в основании которой лежит прямоугольник? Ответы: а)2 б)3 в)1 г)4 д)8 3)Сколько плоскостей симметрии имеет правильная треугольная призма? Ответы: а)4 б)3 в)1 г)2 д)5 г) 5 б) 3 а) 4

Зеркальная симметрия в архитектуре г. Санкт- Петербурга Александринский театр Исаакиевский собор Сколько плоскостей симметрии имеют данные объекты?

Параллельный перенос Параллельным переносом на вектор р называется отображение пространства на себя, при котором любая точка М переходит в такую точку М1, что ММ1 =р М М1 М

A B C D A’ B’ C’ D’ Параллельный перенос

Параллельный перенос является движением. При параллельном переносе на вектор р любые две точки А и В переходят в точки А1и В1 такие, что АА1 = р и BB1= р. Требуется доказать, что А1В1=АВ. По правилу треугольника АВ1 = =АА1+А1 В1 C другой стороны, АВ1=АВ+ВВ1 (рис. 134, б). Из этих двух равенств получаем АА1+А1В1 = AВ + p, или р+А1В1 =АВ+p, откуда А1B1 =АВ. Следовательно, А1В1=АВ, что и требовалось доказать. B1 В

Параллельный перенос Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину. B1 В

В данной презентации рассматриваются такие виды движений как: центральная симметрия, осевая симметрия, зеркальная симметрия.

Содержимое разработки

Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство.

Движение. Виды движения.

Движение пространства –это отображение пространства на себя , сохраняющее расстояние между точками.

Виды движения:

1. Симметрия:

─ осевая,

─ центральная,

─ зеркальная.

2. Параллельный перенос:

ПАРАЛЛЕЛЬНЫЙ ПЕРНОС

Отображение пространства на себя , при котором каждая точка фигуры (тела) перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.

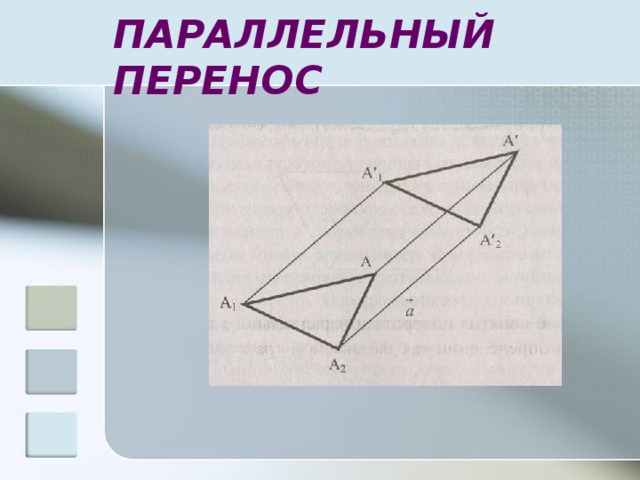
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС

ВЕЛИКИЕ О СИММЕТРИИ…

Леонардо да Винчисчитал, что главную роль в картине играют пропорциональность и гармония, под которыми он понимал симметрию.
Альбрехт Дюрер(1471-1528 г.г.) утверждал, что каждый художник должен знать способы построения правильных симметричных фигур.

ОСЕВАЯ СИММЕТРИЯ

Отображение пространства на себя, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точку А1, называется осевой симметрией.

ЦЕНТРАЛЬНАЯ СИММЕТРИЯ

Отображение пространства на себя, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра т. О, называется центральной симметрией.

ЗЕРКАЛЬНАЯ СИММЕТРИЯ

Зеркальной симметрией (симметрией относительно плоскости a) называется такое отображение плоскости на себя , при котором любая точка переходит в симметричную ей относительно плоскости а точку.

ЗЕРКАЛЬНАЯ СИММЕТРИЯ

СИММЕТРИЯ В АРХИТЕКТУРЕ

Нагляднее всего видна симметрия в архитектуре.
Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие.
В сознании древнегреческих архитекторов симметрия стала олицетворением закономерности, целесообразности, красоты.

СИММЕТРИЯ В АРХИТЕКТУРЕ

Симметрия в жизни

Получите свидетельство о публикации сразу после загрузки работы

Получите бесплатно свидетельство о публикации сразу после добавления разработки

Комплекты учителю

Качественные видеоуроки, тесты и практикумы для вашей удобной работы

Вебинары для учителей

Бесплатное участие и возможность получить свидетельство об участии в вебинаре.

Читайте также: