Что такое комбинаторика сообщение

Обновлено: 07.07.2024

Общие правила комбинаторики, определение понятий множества и факториала. Содержание разделов комбинаторики - перечислительного, экстремального и вероятностного. Понятие о размещении, перестановке и сочетании элементов. Решение комбинаторных задач.

Рубрика	Математика
Вид	реферат
Язык	русский
Дата добавления	21.12.2016
Размер файла	16,8 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Государственное автономное профессиональное образовательное учреждение

"Тобольский медицинский колледж имени Володи Солдатова"

ОСНОВЫ КОМБИНАТОРИКИ

Введение
1. Общие правила комбинаторики
2. Факториал числа
3. Перестановки
4. Размещения
5. Сочетания
6. Решение комбинаторных задач
Заключение
Список литературы

Введение

Число, место и комбинация - три взаимно перекрещивающиеся, но отличные сферы мышления, к которым можно отнести все математические идеи. (Дж. Сильвестр)

На практике часто приходится выбирать из некоторого множества объектов подмножества элементов, обладающих теми или иными свойствами, располагать элементы одного или нескольких множеств в определенном порядке и т.д. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют "комбинаторные задачи".

Комбинаторика занимается различного рода соединениями, которые можно образовать из элементов некоторого конечного множества. Термин "комбинаторика" происходит от латинского combina - сочетать, соединять.

Комбинаторикой называется раздел математики, изучающей вопрос о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов). Наиболее широкое применение комбинаторные задачи находят при решении задач теории вероятностей. Как при решении задач с использованием классического определения вероятности, так и в других ситуациях нам понадобятся некоторые формулы комбинаторики.

На уроке математике мне встретились комбинаторные задачи, которые в последствие заинтересовали меня, и я поставила перед собой цель: рассмотреть шире тему комбинаторика. В дальнейшем поставленная цель позволила мне определить тему реферативной работы.

Для выполнения поставленной цели необходимо решить следующие задачи:

1. Подобрать и изучить литературу по теме реферата.

2. Узнать правила комбинаторики.

3. Узнать виды комбинаторных соединений.

4. Узнать роль факториала числа в комбинаторики.

5. Научиться решать комбинаторные задачи.

1. Общие правила комбинаторики

Комбинаторные задачи бывают самых разных видов. Однако большинство задач решается с помощью двух основных правил -- правила суммы и правила произведения.

Правило суммы

Если некоторый объект A можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор "либо А, либо В" можно осуществить (m+n) способами.

При использовании правила суммы надо следить, чтобы ни один из способов выбора объекта А не совпадал с каким-либо способом выбора объекта В. Если такие совпадения есть, правило суммы утрачивает силу, и мы получаем лишь (m + n - k) способов выбора, где k--число совпадений.

Правило произведения

Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А, В) в указанном порядке можно осуществить mn способами.

При этом число способов выбора второго элемента не зависит от того, как именно выбран первый элемент.

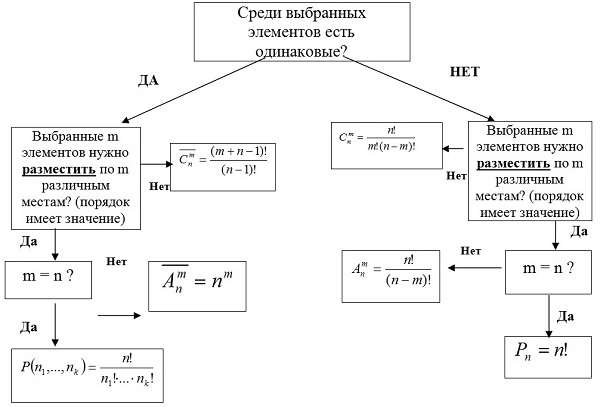
Комбинаторные соединения

Комбинаторные соединения - это такие комбинации из каких-либо элементов.

Существуют две схемы выбора элементов:

2. Факториал числа

Факториал числа - это произведение всех натуральных чисел до этого числа включительно.

Обозначается с восклицательным знаком в конце.

n! = 1 · 2 · 3 · 4 · … · (n-2) · (n-1) · n

Случай 0! определен и имеет значение 0!=1, соответствующее комбинаторной интерпретации комбинации нуля объектов, другими словами, есть единственная комбинация нуля элементов, а именно: пустое множество.

Ниже приведены значения факториалов от 0 до 10.

4! = 1 · 2 · 3 · 4 = 24

5! = 1 · 2 · 3 · 4 · 5 = 120

6! = 1 · 2 · 3 · 4 · 5 · 6 = 720

7! = 1 · 2 · 3 · 4 · 5 · 6 · 7 = 5040

8! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 = 40320

9! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 = 362880

10! = 1 · 2 · 3 · 4 · 5 · 6 · 7 · 8 · 9 · 10 = 3628800

6! = (1 · 2 · 3 · 4 · 5) · 6 = 720

А значение (1 · 2 · 3 · 4 · 5) = 5! = 120

3. Перестановки

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

Формула:

где n! = 1 * 2 * 3 . n.

Перестановки без повторений -- комбинаторные соединения, которые могут отличаться друг от друга лишь порядком входящих в них элементов.

Перестановки с повторениями -- комбинаторные соединения, в которых среди образующих элементов имеются одинаковые. В таких соединениях участвуют несколько типов объектов, причём имеется некоторое количество объектов каждого типа. Поэтому в выборках встречаются одинаковые.

Задача

Сколькими способами можно разместить на странице 5 различных заметок?

Решение: т.к. имеются 5 заметок, и все они участвуют в выборе, то это перестановки. Применим формулу перестановок: Pn=n!, получаем, P5= 5! = 120.

Ответ: Существуют 120 способов разместить имеющиеся заметки.

комбинаторика множество факториал вероятностный

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений

Формула:

A = n (n - 1)(n - 2) . (n - m + 1).

Размещения без повторений - комбинаторные соединения, составленные из n элементов по m. При этом два соединения считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.

Размещения с повторениями - комбинаторные соединения, составленные из n элементов по m. При этом каждый из n элементов может содержаться сколько угодно раз или вообще отсутствовать.

Задача

Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?

Решение: Искомое число сигналов

Ответ: можно составить 30 сигналов.

5. Сочетания

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний

Сочетания без повторений - комбинаторные соединения из n элементов по m, составленные из этих элементов и отличающиеся друг от друга только составом.

Сочетания с повторениями - комбинаторные соединения из n элементов по m, составленные из этих элементов без учета порядка с возможностью многократного повторения предметов.

Задача

Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?

Решение: Искомое число способов

Ответ: 45 способами.

6. Решение комбинаторных задач

Задачу можно назвать комбинаторной, если ее решением является перебор элементов некоторого конечного множества.

Особая примета комбинаторных задач - вопрос, который можно сформулировать, таким образом, что он начинался бы словами:

Для того чтобы решить задачу по комбинаторике, необходимо сначала понять её смысл, то есть, представить мысленно процесс или действие, описанное в задаче.

Нужно чётко определить тип соединений в задаче, а для этого надо, составив несколько различных комбинаций, проверить повторяются ли элементы, меняется ли их состав, важен ли порядок элементов.

Если же комбинаторная задача содержит ряд ограничений, налагающихся на соединения, то нужно понять, как влияют или не влияют эти ограничения на соединения.

В том случае, если трудно сразу определить какие-либо важные моменты задачи, то не плохо было бы попытаться разобраться в более лёгкой задаче, например в той, в которой не учитываются ограничения, если они есть в исходной задаче, или же в задаче, в которой рассматривается меньшее количество элементов, тогда проще будет понять принцип образования выборок.

Когда комбинаторная задача состоит из различных комбинаций элементарных задач, то нужно просто разбить задачу на подзадачи.

В ходе проделанной работы я:

1. Узнал основные правила комбинаторики.

2. Узнал виды комбинаторных соединений.

3. Узнал роль факториала числа в комбинаторики.

4. Научился решать комбинаторные задачи.

Таким образом, я выполнил поставленную цель.

1. А.С. Чесноков, В.И. Жохов, Н.Я. Виленкин, С.И. Шварцбурд Математика 6 класс.

2. Ю.М. Колягин,Ю.В. Сидоров,М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин Алгебра 11 класс.

Подобные документы

Определение понятий множества и факториала. Условия равности двух кортежей. Содержание основных разделов комбинаторики - перечислительного, экстремального и вероятностного. Сущность теории Рамсея. Сведения о размещении, перестановке и сочетании элементов.

реферат [509,5 K], добавлен 21.02.2012

Содержание правил суммы и произведения; их применение с целью решения комбинаторных задач. Виды комбинаторных соединений. Обозначение и свойства факториала. Формулы расчета всех возможных перестановок и размещений. Понятие и разновидности сочетаний.

реферат [22,1 K], добавлен 08.09.2014

Основные принципы и формулы классической комбинаторики. Использование методов комбинаторики в теории вероятностей. Формулы числа перестановок, сочетаний, размещений. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Решение комбинаторных задач.

учебное пособие [659,6 K], добавлен 07.05.2012

Возникновение комбинаторики как раздела математики. Исследование на практических примерах особенностей чисел размещений с повторениями и без них. Анализ задач, решение которых опирается на правила комбинаторики и относящиеся к ней вычислительные формулы.

курсовая работа [175,3 K], добавлен 05.01.2018

дипломная работа [508,5 K], добавлен 26.01.2011

Знакомство с основными понятиями и формулами комбинаторики как науки. Методы решения комбинаторных задач. Размещение и сочетание элементов, правила их перестановки. Характеристики теории вероятности, ее классическое определение, свойства и теоремы.

презентация [1,3 M], добавлен 21.01.2014

Рассмотрение различных примеров комбинаторных задач в математике. Описание способов перебора возможных вариантов. Использование комбинаторного правила умножения. Составление дерева вариантов. Перестановки, сочетания, размещения как простейшие комбинации.

Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов, казалось, долгое время лежала вне основного русла развития математики и ее приложений. На протяжении двух с половиной столетий основную роль в изучении природы играл математический анализ. Процессы, имевшие атомистическую природу, заменялись непрерывными, чтобы можно было применить к ним развитый аппарат математики. Положение коренным образом изменилось после создания быстродействующих вычислительных машин, компьютеров. С их помощью стало возможным делать переборы, ранее требовавшие сотен и тысяч лет. В эпоху расцвета дискретной математики изменилась и роль древнейшей области дискретной математики – комбинаторики. Из области, интересовавшей большей частью составителей занимательных задач и находившей основные применения в кодировании и расшифровке древних письменностей, она превратилась в область, находящуюся на магистральном пути развития науки. Стали выходить журналы по комбинаторике, печататься книги, посвященные этой науке. Элементы комбинаторики находят отражение и в школьном курсе математики.

В нынешнее время комбинаторика имеет огромное значение в различных областях науки и сферы. С комбинаторными величинами приходится иметь дело представителям многих специальностей: ученому – химику, биологу, конструктору, диспетчеру и т.п. Усиление интереса к комбинаторике в последнее время обуславливается бурным развитием кибернетики и вычислительной техники.

Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.

Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.

Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.

Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.

Что такое комбинаторика в математике

Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.

В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.

Основные понятия

Элемент – любой объект или явление, входящий в искомое множество.
Сочетание – подмножества, находящиеся в произвольном порядке в исходном множестве.
Перестановка – элементы во множестве находятся в строго определенном порядке.
Размещение – упорядоченные подмножества в исходном множестве.

Правило произведения

Является одним из основных правил при решении таких задач и звучит так:

При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.

Рассмотрим на конкретных примерах.

Задача №1.

В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?

Ответ прост: 2 * 6 = 12.

Задача №2.

Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?

Решение аналогично: 1 * 2 * 3 * 4 = 24.

Причем левую часть можно записать гораздо проще: 4!

! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).

Задача №3.

Сколько двузначных чисел можно составить из 2 цифр?

Задача №4.

Сколько десятизначных чисел можно составить из 10 цифр?

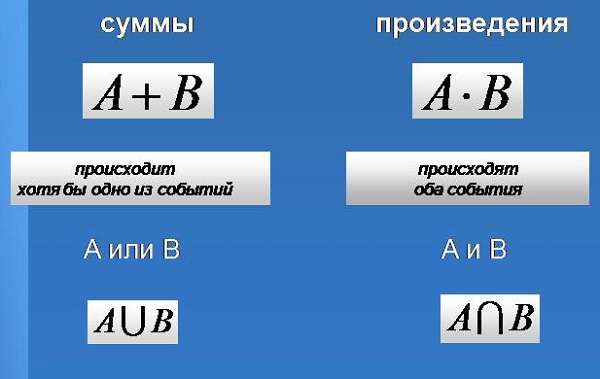
Правило суммы

Тоже является базовым правилом комбинаторики.

Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.

Задача №5.

В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?

Ответ: 5 + 3 + 7 + 9 = 24.

Сочетания с повторениями и без повторений

Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.

Число сочетаний равно количеству таких комбинаций.

Задача №6.

В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?

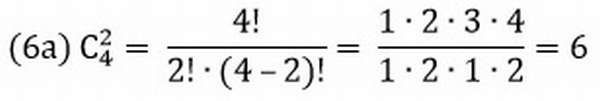
Где 4! – комбинация из 4 элементов.

С повторениями чуть сложней, комбинации считаются по такой формуле:

Задача №7.

Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.

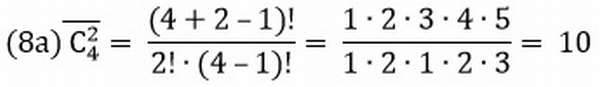
Размещения с повторениями и без повторений

Под этим определением понимают набор m элементов из множества n элементов.

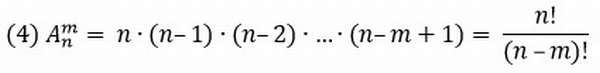
Задача №8.

Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?

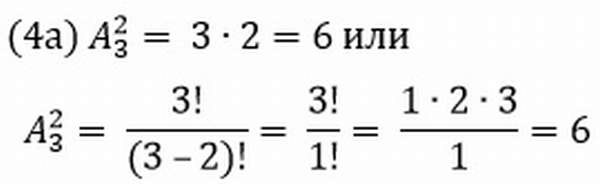
А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:

Задача №9.

Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.

Перестановки с повторениями и без повторений

Под этим термином понимают все возможные комбинации из n элементного множества.

Задача №10.

Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?

Решения, согласно вышеприведенной формуле, следующие:

А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!

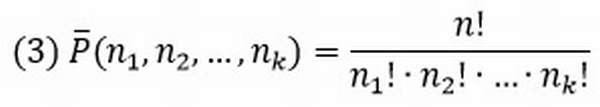
Задача №11.

В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?

Ответ прост: 4! / (3! * 1!) = 4.

Комбинаторные задачи с решениями

Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.

Типы задач	Что требуется найти	Методы решения
Магический квадрат	Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат).	Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам.
Задача размещения	Стандартная производственная задача (например, в лоскутной технике) найти возможные способы разложения количества продуктов в ячейки в определенном порядке.	Включения и исключения. Как правило, применяется при доказательстве различных выражений.
Задачи про торговцев	Суть найти все возможные пути прохождения людей из пункта А в пункт В.	Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения.

Заключение

Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.

Часто приходится иметь дело с задачами выбора элементов из некоторой совокупности и расположения этих элементов в определенном порядке. Поскольку в таких задачах речь идет о тех или иных комбинациях объектов, их называют комбинаторными задачами. Роль таких задач важна не только в математике, но и физике, химии, биологии, технике и экономике. Комбинаторные задачи приходится рассматривать при определении наиболее выгодных коммуникаций внутри города, при организации автоматической телефонной связи, при выявлении связей внутри сложных молекул, генетического кода, математической статистики и т. д.

Вложение	Размер
kombinatorika.docx	38.96 КБ
kombinatorika.pptx	325.58 КБ

Предварительный просмотр:

Муниципальное автономное общеобразовательное учреждение

средняя общеобразовательная школа № 147

Выпoлнил: ученик 4 А клacca

Глава I. 1.1. Исторические сведения о комбинаторике ………………….

Глава II. Исследовательская часть ……………………………….

Список используемых источников и литературы ………………………..

Трудно переоценить значимость той роли, которую играет обучение методам решения комбинаторных задач в общеобразовательной школе. Освоение методов решения таких задач способствует развитию умственных способностей и математического кругозора ученика. Комбинаторные задачи несут широкие возможности для способов решения таких задач, которые могут служить как формы общих методов решения задач.

Основной темой и предметом данного исследования является —

Комбинато́рика — раздел математики , изучающий дискретные объекты, множества ( сочетания , перестановки , размещения и перечисления элементов).

Объект исследования : область математики – комбинаторика.

Цель работы: знакомство с понятием комбинаторика. Расширить область математических знаний. Развивать логическое мышление.

Гипотеза : комбинаторика интересна и имеет широкий спектр практической направленности.

Собрать, изучить и систематизировать материал о комбинаторике;
Рассмотреть, как элементы комбинаторики используются при решении различных жизненных ситуаций;
Использование комбинаторики в различных сферах жизнедеятельности.

Термин "комбинаторика" был введён в математический обиход знаменитым Лейбницем. Готфрид Вильгельм Лейбниц (1.07.1646 — 14.11.1716) — всемирно известный немецкий учёный, занимался философией, математикой, физикой, организовал Берлинскую академию наук и стал её первым президентом.

В 1666 году Лейбниц (ему было тогда 20 лет) опубликовал "Рассуждения о комбинаторном искусстве". В своём сочинении Лейбниц, вводя специальные символы, термины для подмножеств и операций над ними находит все k —сочетания из n элементов выводит свойства сочетаний.

В течение всей своей жизни Лейбниц многократно возвращался к идеям комбинаторного искусства. Комбинаторику он понимал весьма широко, именно, как составляющую любого исследования, любого творческого акта, предполагающего сначала анализ (расчленение целого на части), а затем синтез (соединение частей в целое).

В XVIII веке к решению комбинаторных задач обращались выдающиеся математики. Так, Леонард Эйлер рассматривал задачи о разбиении чисел, о паросочетаниях, о циклических расстановках, о построении магических и латинских квадратов.

В 1713 году было опубликовано сочинение Я. Бернулли "Искусство предположений", в котором были изложены известные к тому времени комбинаторные факты и содержались формулы:

для числа перестановок из n элементов
для числа сочетаний без повторений и с повторениями,
для числа размещений с повторениями и без повторений.

Комбинаторика, пройдя многовековой путь развития, обретя собственные методы исследования, с одной стороны, широко используется при решении задач алгебры, геометрии, анализа, с другой стороны, сама использует геометрические, аналитические и алгебраические методы исследования.

В XX веке комбинаторика подверглась мощному процессу алгебраизации благодаря работам Дж.-К. Рота (1964), а затем Р. Стенли. Изучение ими частично упорядоченных множеств, свойств функции Мёбиуса, абстрактных свойств линейной зависимости, выявление их роли при решении комбинаторных задач способствовали обогащению комбинаторных методов исследования и дальнейшей интеграции комбинаторики в современную математику.

обусловлена предоставляемой ею возможностью решать практические задачи при помощи стандартных алгоритмов и формализованных алгебраических методов.

Меня комбинаторика привлекла интересными задачами, неожиданными решениями и результатами, новым взглядом на повседневные события. Для меня стало открытием, что многие казавшиеся непредсказуемыми процессы (даже протекающие в нашем классе!) подчиняются строгим математическим законам. Жаль, что комбинаторике уделяется так мало внимания в курсе начальной школы.

2.1. Исследовательская часть

Исследовать задачи, изучаемые комбинаторикой, я предлагаю на примере нашего класса. У нас в классе 22 ученика; 10 мальчиков, 12 девочек. Нашу учительницу зовут Наталья Матвеевна.

Видно, что от каждого кружочка-ученика отходят стрелочки к 21 другому кружочку и приходит тоже 21 стрелочка.

Похоже, этот праздник придумали продавцы открыток!

22 ученика поздравили друг друга по телефону с Новым годом. Сколько всего было сделано звонков?

Видно, что стрелок здесь в 2 раза меньше, стрелочки двойные так как одним разговором поздравляют друг друга сразу 2 человека.

231 звонок, тоже немало!

У Марка есть карточки с цифрами 3, 5, 6; у Саши 0, 1,2; а у Ильи 6, 8, 8. Ребята поспорили, кто из них составит больше чисел из своих цифр?

Решим задачу перебором:

0 первым в числе быть не может

У Марка 6 чисел, у Саши 4 числа, у Ильи 3 числа.

А если числа могут повторяться, методом перебора получится:

У Марка 27 чисел, у Саши 18 чисел, у Ильи 8 чисел.

Сколькими способами Наталья Матвеевна может рассадить 22 ученика за 11 парт?

Перебором эту задачу решать сложно, воспользуемся формулой о числе возможных перестановок

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

где n! = 1 * 2 * 3 . n.

22!=22*21*…2*1=1124000000000000000000 (считала программа Excel)

18 нулей! Даже если мы будем пересаживаться каждый урок все 4 года без выходных и каникул (365*4*4=35040) все равно перебрать все варианты не успеем!

Сколькими способами Наталья Матвеевна может из 22 учеников выбрать 3 дежурных?

Воспользуемся формулой о числе возможных сочетаний:

С m n = n! / (m! (n - m)!).

22!/(3!*(22-3)!)=1540 сам считал!

В предыдущей задаче мы подсчитали что из 22 учеников по 3 можно сделать 1540 выборок,

1540*6=9240 способов распределить рефераты ребятам.

Ну все таки меньше чем способов рассадить за парты!

Задача 7 (принцип Дирихле)

В нашем классе 22 ученика, Докажите, что хотя бы у двоих день рождения в одном месяце.

В году 12 месяцев, если в каждом месяце день рождения 1 ученика

22-12=10 ребят останутся без дня рождения, значит у нескольких дни рождения должны быть в один месяц.

Задача 8 (принцип Дирихле)

В коробке 10 красных, 10 синих, 5 зеленых и 5 желтых карандашей. Девочки достают карандаши из коробки, не глядя, какое минимальное число карандашей надо достать чтобы:

У Оли было не менее 2 карандашей одного цвета?

В худшем случае Оля сначала вытащит 1 красный, 1 синий, 1 зеленый и 1 желтый, любой следующий карандаш совпадет по цвету с каким-то предыдущим.

Оле надо взять не менее 5 карандашей.

У Алены было не менее 5 красных?

В худшем случае Алена сначала вытащит 4 красных, 10 синих, 5 зеленых и 5 желтых, следующий карандаш точно будет пятым красным.

Алене надо взять не менее (5+10+5+5) =25 карандашей.

У Кати было по одному карандашу каждого цвета?

В худшем случае Катя сначала вытащит 10 красных, 10 синих, 5 зеленых (или 5 желтых), следующий карандаш точно будет последним недостающим.

Кате надо взять не менее (10+10+5+1) =26 карандашей.

Используя методы комбинаторики, наши девочки даже с завязанными глазами возьмут наименьшее количество карандашей, чтобы получить требуемые цвета. В нашем классе очень умные, бойкие и красивые девочки!

Комбинаторика очень интересная наука, если применить ее к нашему классу получаются потрясающие результаты! Чтобы перепробовать все возможные пересадки за партами, варианты троек для дежурства и т.д. нам не хватит 11 школьных лет!

Мне решение задач на комбинаторику позволило по-новому взглянуть на изучаемые в школе разделы математики, надеюсь, это поможет в дальнейшем освоении формальной логики алгебры.

Предлагаю шире изучать комбинаторику в школе; например, во время занятий кружков и факультативов.

Дальнейшее изучение комбинаторики, логически предполагает рассмотрение применения простейших формул теории вероятности к жизни нашего класса.

Список используемых источников и литературы

Предварительный просмотр:

Подписи к слайдам:

История комбинаторики Выпoлнил : ученик 4 А класса Гуcев Дмитрий Руководитель: Вырышевa Нaтaлья Мaтвеевнa

Объект исследования : область математики – комбинаторика. Цель работы: знакомство с понятием комбинаторика. Расширить область математических знаний. Развивать логическое мышление. Гипотеза : комбинаторика интересна и имеет широкий спектр практической направленности.

Задачи исследования : Собрать, изучить и систематизировать материал о комбинаторике; 2. Рассмотреть, как элементы комбинаторики используются при решении различных жизненных ситуаций; 3. Использование комбинаторики в различных сферах жизнедеятельности.

Комбинато́рика — раздел математики , изучающий дискретные объекты, множества ( сочетания , перестановки , размещения и перечисления элементов). В разное время комбинаторикой занимались: Готфрид Лейбниц (1646-1716) Леонард Эйлер (1707-1783) Якоб Бернулли (1654-1705) Комбинаторика – древняя наука!

22 ученика поздравили друг друга по телефону с Новым годом. Сколько всего было сделано звонков? Сделаем рисунок: Видно, что стрелок здесь в 2 раза меньше, стрелочки двойные так как одним разговором поздравляют друг друга сразу 2 человека. 22*21:2=231 звонок 231 звонок, тоже немало! Задача № 2 22 1 2 3 4 21 …

У Марка есть карточки с цифрами 3, 5, 6; у Саши 0, 1, 2; а у Ильи 6, 8, 8. Ребята поспорили, кто из них составит больше чисел из своих цифр? Решим задачу перебором: У Марка 6 чисел, у Саши 4 числа, у Ильи 3 числа. А если числа могут повторяться, методом перебора получится: У Марка 27 чисел, у Саши 18 чисел, у Ильи 8 чисел. Марк Саша Илья 357 375 573 537 753 735 240 204 420 402 0 первым в числе быть не может 688 868 886 Задача № 3

Сколькими способами Наталья Матвеевна может рассадить 22 ученика за 11 парт? Перебором эту задачу решать сложно, воспользуемся формулой о числе возможных перестановок. Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок P n = n !, где n ! = 1 * 2 * 3 . n . 22!=22*21*…2*1=1124000000000000000000 ( считала программа Excel ) 18 нулей! Даже если мы будем пересаживаться каждый урок все 4 года без выходных и каникул (365*4*4=35040) все равно перебрать все варианты не успеем! Задача № 4

Сколькими способами Наталья Матвеевна может из 22 учеников выбрать 3 дежурных? Воспользуемся формулой о числе возможных сочетаний: Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний С m n = n ! / ( m ! ( n - m )!). 22!/(3!*(22-3)!)=1540 сам считал! Задача № 5

В коробке 10 красных, 10 синих, 5 зеленых и 5 желтых карандашей. Девочки достают карандаши из коробки, не глядя, какое минимальное число карандашей надо достать чтобы: 10 У Оли было не менее 2 карандашей одного цвета? В худшем случае Оля сначала вытащит 1 красный, 1 синий, 1 зеленый и 1 желтый, любой следующий карандаш совпадет по цвету с каким-то предыдущим. Оле надо взять не менее 5 карандашей. У Алены было не менее 5 красных? В худшем случае Алена сначала вытащит 4 красных, 10 синих, 5 зеленых и 5 желтых, следующий карандаш точно будет пятым красным. Алене надо взять не менее (5+10+5+5) =25 карандашей. Задача № 7 (принцип Дирихле) У Кати было по одному карандашу каждого цвета? В худшем случае Катя сначала вытащит 10 красных, 10 синих, 5 зеленых (или 5 желтых), следующий карандаш точно будет последним недостающим. Кате надо взять не менее (10+10+5+1) =26 карандашей.

Вывод Комбинаторика очень интересная наука, если применить ее к нашему классу получаются потрясающие результаты! Чтобы перепробовать все возможные пересадки за партами, варианты троек для дежурства и т.д. нам не хватит 11 школьных лет!

Читайте также: