Сочинение на тему призма
Обновлено: 05.07.2024
Подобно тому, как треугольник в понимании Евклида не являются пустым , т. е. представляет собой часть плоскости , ограниченную тремя неконкурентными (т. е. не пересекающимися в одной точке) отрезками, так и многогранник у него не пустой, не полый, а чем-то заполненный (по-нашему - частью пространства). В античной математике, однако, понятия отвлеченного пространства еще не было. Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и с боковыми гранями - параллелограммами. Для того чтобы это определение было вполне корректным, следовало бы, однако, доказать, что плоскости, проходящие через пары непараллельных сторон оснований, пересекаются по параллельным прямым. Евклид употребляет термин “плоскость” как в широком смысле (рассматривая ее неограниченно продолженной во все направления), так и в смысле конечной, ограниченной ее части, в частности грани , аналогично применению им термина “прямая” (в широком смысле - бесконечная прямая и в узком - отрезок). В XVIII в. Тейлор дал такое определение призмы : это многогранник, у которого все грани, кроме двух, параллельны одной прямой.
Пирамиду Евклид определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости (основания) сходятся в одной точке (вершине). Эго определение подвергалось критике уже в древности, например, Героном, предложившим следующее определение пирамиды: это фигура, ограниченная треугольниками, сходящимися в одной точке, и основанием которой служит многоугольник.
Важнейшим недостатком этого определения является использование неопределенного понятия основания. Тейлор определил пирамиду как многогранник, у которого все грани, кроме одной, сходятся в одной точке. Лежандр в “Элементах геометрии” так определяет пирамиду: “Телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания”. После этой формулировки разъясняется понятие основания. Определение Лежандра является явно избыточным, т.е. содержит признаки, которые можно вывести из других. А вот еще одно определение, которое фигурировало в учебниках ХIХ в.: пирамида - телесный угол, пересеченный плоскостью.
Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела , линию - как границу поверхности , концы же линии - как точки . Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д. Одним из первых, который соединил обе эти точки зрения, был Герон Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности. В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а иногда и обе вместе точки зрения.
2.3. Пирамида и площадь ее поверхности
Определение. Многогранник, одна из граней которого - многоугольник, а остальные грани - треугольники с общей вершиной, называется пирамидой.
На рисунке изображены пятиугольная пирамида SABCDE и ее развертка. Треугольники, имеющие общую вершину, называют боковыми гранями пирамиды; общую вершину боковых граней - вершиной пирамиды; многоугольник, которому не принадлежит эта вершина,- основанием пирамиды; ребра пирамиды, сходящиеся в ее вершине,- боковыми ребрами пира-
миды. Высота пирамиды - это отрезок перпендикуляра, проведенного через ее вершину к плоскости основания, с концами в вершине и на плоскости основания пирамиды. На рисунке отрезок SO - высота пирамиды.
Определение. Пирамида, основание которой - правильный многоугольник и вершина проектируется в его центр, называется правильной.
На рисунке изображена правильная шестиугольная пирамида.
2.4. Измерение объемов
Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту. Однако древнему Востоку были известны в основном только отдельные правила, найденные опытным путем, которыми пользовались для нахождения объемов для площадей фигур. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников.
Среди замечательных греческих ученых V - IV вв. до н.э., которые разрабатывали теорию объемов, были Демокрит из Абдеры и Евдокс Книдский.
Евклид не применяет термина “объем”. Для него термин “куб”, например, означает и объем куба. В ХI книге “Начал” изложены среди других и теоремы следующего содержания.
1. Параллелепипеды с одинаковыми высотами и равновеликими основаниями равновелики .
2. Отношение объемов двух параллелепипедов с равными высотами равно отношению площадей их оснований .
3. В равновеликих параллелепипедах площади оснований обратно пропорциональны высотам .
Теоремы Евклида относятся только к сравнению объемов, так как непосредственное вычисление объемов тел Евклид, вероятно, считал делом практических руководств по геометрии. В произведениях прикладного характера Герона Александрийского имеются правила для вычислений объема куба, призмы, параллелепипеда и других пространственных фигур.
2.5. О пирамиде и ее объеме
Термин “пирамида” заимствован из греческого “пирамис” или “пирамидос”. Греки в свою очередь позаимствовали это слово, как полагают, из египетского языка. В папирусе Ахмеса встречается слово “пирамус” в смысле ребра правильной пирамиды. Другие считают, что термин берет свое начало от форм хлебцев в Древней Греции “пирос” - рожь). В связи с тем, что форма пламени иногда напоминает образ пирамиды, некоторые средневековые ученые считали, что термин происходит греческого слова “пир” - огонь. Вот почему в некоторых учебниках геометрии XVI в. пирамида названа “огнеформное тело”.
В Древнем Египте гробницы фараонов имели форму пирамид. В III Тысячелетии до н.э. египтяне сооружали ступенчатые пирамиды, сложенные из каменных блоков; позже египетские пирамиды приобрели геометрически правильную форму, например пирамида Хеопса, высота которой достигает почти 147 м, и др. Внутри пирамид находились погребальные склепы и коридоры.
Согласно Архимеду, еще в V до н.э. Демокрит из Абдеры установил, что объем пирамиды равен одной трети объема призмы с тем же основанием и той же высотой. Полное доказательство этой теоремы дал Евдокс Книдский в IV до н.э.
В “Началах” Евклида доказывается, что в равновеликих пирамидах площади оснований обратно пропорциональны соответствующим высотам. Первое непосредственное вычисление объема пирамиды, дошедшее до нас, встречается у Герона Александрийского.
Интересно отметить, что в древних документах встречаются правила для определения объема усеченной пирамиды, о нет правил вычисления объема полной пирамиды. В “Московском папирусе” имеется задача, озаглавленная “Действия с усеченной пирамидой”, в которой излагается верное вычисление объема одной усеченной пирамиды. В вавилонских клинописных табличках также не встречается вычисление объема пирамиды, но зато в них есть много примеров вычисления объема усеченной пирамиды.
2.6. О призме и параллелепипеде
В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения.
Часть геометрии, в которой изучаются свойства куба, призмы, параллелепипеда и других геометрических тел и пространственных фигур, издавна называется стереометрией; Слово это греческого происхождения (“стереос” - пространственный, “метрео” - измеряю) и встречается еще у знаменитого древнегреческого философа Аристотеля. Стереометрия возникла позже, чем планиметрия. Евклид дает следующее определение призмы: “Призма есть телесная (т.е. пространственная) фигура, заключенная между плоскостями, из которых две противоположные равны и параллельны, остальные же - параллелограммы”. Тут, как и во многих других местах, Евклид употребляет термин “плоскость” не в смысле безгранично продолженной плоскости, а в смысле ограниченной ее части, грани, подобно тому как “прямая” означает у него и отрезок прямой.
Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело).
Термин “параллелепипедальное тело” встречается впервые у Евклида и означает дословно “параллеле-плоскостное тело”. Греческое слово “кубос” употребляется Евклидом в том же смысле, что и наше слово “куб”
Многоугольники, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани — боковыми гранями.
Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.
Все призмы делятся на прямые и наклонные .
(рис. 2)
Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани — прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы.
Свойства призмы
1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы являются параллелограммами.
3. Боковые ребра призмы равны.
Площадь поверхности призмы и площадь боковой поверхности призмы
— Поверхность многогранника состоит из конечного числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм (S пр) равна сумме площадей ее боковых граней (площади боковой поверхности S бок) и площадей двух оснований (2S осн) — равных многоугольников: S пов=S бок+2S осн.
— Теорема. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.
Боковые грани прямой призмы — прямоугольники, основания которых-стороны основания призмы, а высоты равны высоте h призмы. Sбок поверхности призмы равна сумме S указанных треугольников, т.е. равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки, получим в скобках сумму сторон основания призмы, т.е. периметр P. Итак, Sбок =Ph. Теорема доказана.
Следствие. Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты.
Действительно, у прямой призмы основание можно рассматривать как перпендикулярное сечение, а боковое ребро есть высота.
Сечение призмы
— 1. Сечение призмы плоскостью, параллельной основанию. В сечении образуется многоугольник, равный многоугольнику, лежащему в основании.
— 2. Сечение призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется параллелограмм. Такое сечение называется диагональным сечением призмы. В некоторых случаях может получаться ромб, прямоугольник или квадрат.
Определение 2
Прямая призма , основанием которой служит правильный многоугольник, называется правильной призмой.
Свойства правильной призмы
1. Основания правильной призмы являются правильными многоугольниками.
2. Боковые грани правильной призмы являются равными прямоугольниками.
3. Боковые ребра правильной призмы равны.
Сечение правильной призмы
1. Сечение правильной призмы плоскостью, параллельной основанию. В сечении образуется правильный многоугольник, равный многоугольнику, лежащему в основании.
2. Сечение правильной призмы плоскостью, проходящей через два не соседних боковых ребра. В сечении образуется прямоугольник. В некоторых случаях может образоваться квадрат.
Симметрия правильной призмы
1. Центр симметрии при четном числе сторон основания — точка пересечения диагоналей правильной призмы (рис. 6)
2. Плоскости симметрии: плоскость, проходящая через середины боковых ребер; при четном числе сторон основания — плоскости, проходящие через противолежащие ребра (рис. 7).
— 3. Оси симметрии: при четном числе сторон основания — ось симметрии, проходящая через центры оснований, и оси симметрии, проходящие через точки пересечения диагоналей противолежащих боковых граней (рис. 8).
Дано: Сторона основания правильной треугольной призмы равна 8 см, боковое ребро — 6 см. Найдите S сеч, проходящего через сторону верхнего основания и противолежащую вершину нижнего основания.
Решение: Треугольник A1 B1 C1 — равнобедренный(A1 B=C1 B как диагональ равных граней)
Рассмотрим произвольный многоугольник, например, пятиугольник АВСDЕ (см. чертеж на стр. 25), который лежит в плоскости a . Рассмотрим теперь параллельный перенос, определяемый некоторым ненулевым вектором V , не лежащим в плоскости. Образом плоскости a будет параллельная ей плоскость b . Образом многоугольника Ф будет многоугольник Ф 1 = A 1 B 1 C 1 D 1 E 1 , лежащий в плоскости b . Направленные отрезки AA 1 , BB 1 будут параллельны, так как каждый из них изображает один и тот же вектор V . Многогранник ABCDEA 1 B 1 C 1 D 1 E 1 называют призмой.
Определение 1. Многогранник, две грани которого - одноименные многоугольники, лежащие в параллельных плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны, называется призмой.
Многоугольники Ф и Ф 1 , лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями .
Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания
Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой ; если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют наклонной . У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы. На рис. отрезок A 1 O - высота изображенной призмы.
Определение 2. Прямая призма, основанием которой служит правильный многоугольник, называется правильной призмой.
Боковое ребро прямой призмы, в том числе и правильной, есть ее высота. На рисунке изображена правильная шестиугольная призма и ее разверстка; высота этой призмы равна ее боковому ребру. Отрезок, концы которого - две вершины, не принадлежащие одной грани призмы, называют ее диагональю . Отрезок B 1 D (см. рис. ) - диагональ призмы. Сечение призмы с плоскостью, проходящей через два боковых ребра, не лежащих в одной грани, называют диагональным сечением призмы.
2.1 Площадь поверхности призмы
Поверхность многогранника состоит из конечного числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм ( S пр ) равна сумме площадей ее боковых граней (площади боковой поверхности S бок ) и площадей двух оснований (2 S осн ) - равных многоугольников: S пр = S бок +2 S осн .
Теорема. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.
Дано: АС 1 - произвольная n -угольная призма (на рисунке в качестве примера изображена четырехугольная призма), a^ AA 1 , A 2 B 2 C 2 D 2 - перпендикулярное сечение (сечение призмы плоскостью, перпендикулярной боковому ребру), l - длина бокового ребра.
Доказать: S бок = Р l , где Р - периметр перпендикулярного сечения.
Доказательство. S бок = S AA 1 B 1 B + S BB 1 C 1 C + S CC 1 D 1 D +.
Каждая боковая грань призмы - параллелограмм, основание которого - боковое ребро призмы, а высота - сторона перпендикулярного сечения
S бок = lA 2 B 2 + lB 2 C 2 + lC 2 D 2 +. =( A 2 B 2 + B 2 C 2 + C 2 D 2 +. ) l = P l .
Следствие. Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты.
Действительно, у прямой призмы основание можно рассматривать как перпендикулярное сечение, а боковое ребро есть высота
2.2. Призма и пирамида
Подобно тому, как треугольник в понимании Евклида не являются пустым , т. е. представляет собой часть плоскости , ограниченную тремя неконкурентными (т. е. не пересекающимися в одной точке) отрезками, так и многогранник у него не пустой, не полый, а чем-то заполненный (по-нашему - частью пространства). В античной математике, однако, понятия отвлеченного пространства еще не было. Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и с боковыми гранями - параллелограммами. Для того чтобы это определение было вполне корректным, следовало бы, однако, доказать, что плоскости, проходящие через пары непараллельных сторон оснований, пересекаются по параллельным прямым. Евклид употребляет термин “плоскость” как в широком смысле (рассматривая ее неограниченно продолженной во все направления), так и в смысле конечной, ограниченной ее части, в частности грани , аналогично применению им термина “прямая” (в широком смысле - бесконечная прямая и в узком - отрезок). В XVIII в. Тейлор дал такое определение призмы : это многогранник, у которого все грани, кроме двух, параллельны одной прямой.
Пирамиду Евклид определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости (основания) сходятся в одной точке (вершине). Эго определение подвергалось критике уже в древности, например, Героном, предложившим следующее определение пирамиды: это фигура, ограниченная треугольниками, сходящимися в одной точке, и основанием которой служит многоугольник.
Важнейшим недостатком этого определения является использование неопределенного понятия основания. Тейлор определил пирамиду как многогранник, у которого все грани, кроме одной, сходятся в одной точке. Лежандр в “Элементах геометрии” так определяет пирамиду: “Телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания”. После этой формулировки разъясняется понятие основания. Определение Лежандра является явно избыточным, т.е. содержит признаки, которые можно вывести из других. А вот еще одно определение, которое фигурировало в учебниках ХIХ в.: пирамида - телесный угол, пересеченный плоскостью.
Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела , линию - как границу поверхности , концы же линии - как точки . Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д. Одним из первых, который соединил обе эти точки зрения, был Герон Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности. В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а иногда и обе вместе точки зрения
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Доклад по теме: Стереометрия. Призма.
Стереометрия – раздел геометрии, в котором изучаются свойства пространственных фигур, то есть фигур, не принадлежащих одной плоскости. В стереометрии рассматриваются различные случаи взаимного расположения прямых и плоскостей в пространстве, такие пространственные фигуры, как призма, пирамида, тела вращения, правильные многогранники и др.
Призма - многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками. Или (равносильно) — это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани — параллелограммы. Призма является разновидностью цилиндра.

Свойства призмы
· Основания призмы являются равными многоугольниками.
· Боковые грани призмы являются параллелограммами.
· Боковые ребра призмы параллельны и равны.
· Объём призмы равен произведению её высоты на площадь основания:
· Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
· Площадь боковой поверхности прямой призмы:
· Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы.
· Углы перпендикулярного сечения -- это линейные углы двугранных углов при соответствующих боковых рёбрах.
· Перпендикулярное сечение перпендикулярно ко всем боковым граням.
Призма, основанием которой является параллелограмм, называется параллелепипедом.
Прямая призма - это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.
Правильная призма - это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы - равные прямоугольники.
Правильная призма, боковые грани которой являются квадратами (высота которой равна стороне основания), является полуправильным многогранником.
Элементы призмы

Основания - 2 грани, являющиеся равными многоугольниками, которые лежат в плоскостях, параллельных друг другу.
Боковые грани - каждая из граней, не считая оснований. Все боковые грани - это параллелограммы.
Боковая поверхность - сумма боковых граней.
Полная поверхность - сумма основания и боковой поверхности.
Боковые ребра - общие стороны боковых граней.
Высота - отрезок, который соединяет плоскости, в них лежат основания призмы. Он перпендикулярен этим плоскостям.
Диагональ - отрезок, который соединяет 2 вершины призмы, которые не принадлежат одной грани.
Диагональная плоскость - плоскость, которая проходит через боковое ребро призмы, а также диагональ основания.
Диагональное сечение - пересечение призмы и диагональной плоскости. В сечении получается параллелограмм, либо -- ромб, прямоугольник, квадрат.
Перпендикулярное сечение - пересечение призмы и плоскости, перпендикулярной боковому ребру призмы.
Развертка призмы - представление всех граней призмы на одной плоскости без искажения размеров граней.
Школьники сталкиваются с ней на уроках геометрии только в 10 классе. Соответственно, те, кто решил уйти после 9-го класса в колледж, этих знаний лишены. И мы восполним этот пробел.
А старшеклассникам наша статья (очень на это надеемся) поможет при подготовке к сдаче ЕГЭ. На экзаменах по математике попадаются несколько вопросов, связанных с ПРИЗМАМИ.
Призма – это .
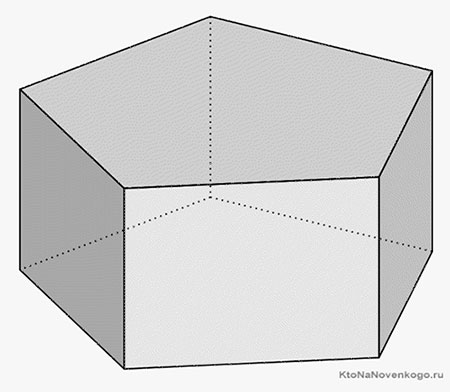
Призма – это геометрическая фигура, которая представляет собой объемный многогранник. Две его стороны лежат на параллельных основаниях и представляют собой различные многоугольники. А боковые грани – это параллелограммы, которые соединяются с основаниями.

Выглядит классическая призма так, как показано на рисунке выше.
На этом рисунке четко видны все элементы призмы:
- Основание – два многоугольника, которые параллельны друг другу;
- Боковые грани – четырехугольники, которые скрепляют оба основания и имеют с ними одинаковые грани.
В зависимости от вида основания призмы бывают:
-
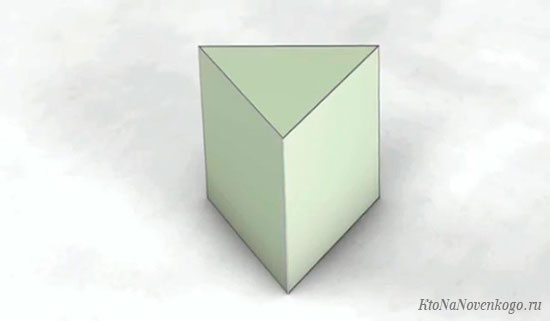
Треугольные – в основаниях находятся два треугольника.


Разнообразие призм можно считать бесконечным. Могут быть фигуры, у которых в основании и 10-угольник, и 20-угольник, и даже 100-угольник. Но, к счастью, такие фигуры попадаются крайне редко. И их точно не изучают в школе.
История изучения призмы
О существовании призм знали еще в Древнем Египте и Древнем Вавилоне. Об этом свидетельствуют различные археологические находки, прежде всего, остатки зданий и памятников.
И в рамках этой науки Аристотель занимался изучением призм, кубов, параллелепипедов и других объемных геометрических фигур.

Естественно, не обошел своим вниманием призмы и знаменитый древнегреческий математик и ученый – Евклид. В своих трудах он дает следующее описание:
Призма – это телесная (то есть пространственная) фигура, которая заключена между несколькими плоскостями. Две из них параллельны друг другу, равны и противоположны. А другие в любом количестве представляют собой параллелограммы.
Элементы призмы
Рассмотрим для примера такую вот призму.

Она пятиугольная и состоит из следующих элементов:
- Основание – их, как и положено, две штуки, в данном случае это пятиугольники ABCDE и KLMNP;
- Боковая грань – их количество равно количеству углов оснований, то есть тоже пять. Это параллелограммы ABKL, BCLM, CDMN, DENP и EAPK;
- Боковая поверхность – так называют сумму всех имеющихся боковых граней, которые мы перечислили выше;
- Полная поверхность – это сумма всех частей призмы;
- Боковое ребро – линии соединения боковых граней. В нашем случае это отрезки KA, LB, MC, ND и PE;
- Высота – отрезок, который соединяет основания призмы под прямым углом. В нашем случае KR. Это касается наклонных призм, у которых грани не перпендикулярны основаниям. В противном случае, высота совпадает с боковым ребром;
- Диагональ – отрезок (PВ), который соединяет две вершины призмы, не относящиеся к одной грани;
- Диагональная плоскость – плоскость, которая проходит через основание, боковую грань и диагональ. В нашем случае это BPE и BPL;
- Диагональное сечение – плоскость, которая образуется пересечением призмы и диагональной плоскостью. В нашем случае это параллелограмм BLPE. В частных случаях она может быть ромбом или квадратом.
Подобные элементы есть у каждой призмы, независимо от ее вида.
Разновидности призм
Все призмы можно поделить на три категории:
-
Прямая призма – эта такая геометрическая фигура, у которой боковые грани соединяются с основаниями под прямым углом. Соответственно, они являются прямоугольниками. А саму призму часто еще называют прямоугольным параллелепипедом.



Вместо заключения
Слово ПРИЗМА используется не только в геометрии, хотя именно это значение считается главным. И именно оно первым записано во многих словарях. Но есть и другие варианты:
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Спасибо! Хорошая статья.
Бедные дети, зачем им забивают голову всякими геометрическими призмами? Вообще, если провести опрос среди взрослых, понадобилось ли кому-нибудь это знание, уверен, мы не услышим ни одного положительного ответа.
Читайте также:
- Напишите сочинение рассуждение объясните как вы понимаете смысл предложения 52 текста она спасала
- Птухина учимся писать сочинение 1 класс скачать бесплатно
- Сочинение корень учения горек да плод его сладок
- Достоевский преступление и наказание краткое содержание сочинение
- Талант есть драгоценнейший дар бога не погуби его сочинение

