Энтропия непрерывных сообщений кратко

Обновлено: 02.07.2024

Энтропия непрерывного источника информации

Энтропия непрерывного источника информации должна быть бесконечна, т. к. неопределенность выбора из бесконечно большого числа возможных состояний бесконечно велика. (на самом деле это только некорректная математическая модель, так как реальные сигналы занимают ограниченный спектр частот, а значит, могут быть представлены дискретными значениями через некоторый шаг, определяемый теоремой Котельникова; кроме того реальные сигналы не могут быть измерены с бесконечной точностью, так как имеются шумы линии и ошибка измерения, а это значит, что по шкале динамического диапазона непрерывный сигнал тоже может быть представлен конечным числом различимых квантовых уровней - примечание К.А. Хайдарова)

Разобьем диапазон изменения непрерывной случайной величины U на конечное число n малых интервалов D u. При реализации значений u в интервале (u n , u n + D u) будем считать, что реализовалось значение u n дискретной случайной величины U', вероятность реализации которой:

Энтропия дискретной величины U':

H(U') = -p(u n ) D u log (p(u n ) D u).

Заменяем log (p(u n ) D u) = log p(u n )+log D u, принимаем во внимание, что сумма p(u n ) D u по всем возможным значениям u n равна 1, и получаем:

H(U') = -p(u n ) D u log p(u n ) – log D u. (1.4.4)

В пределе, при D u ® 0, получаем выражение энтропии для непрерывного источника:

H(U) = -p(u) log p(u) du –. (1.4.5)

Значение энтропии в (1.4.5), как и ожидалось, стремится к бесконечности за счет второго члена выражения. Для получения конечной характеристики информационных свойств непрерывных сигналов используют только первый член выражения (1.4.5), получивший название дифференциальной энтропии . Ее можно трактовать, как среднюю неопределенность выбора произвольной случайной величины по сравнению со средней неопределенностью выбора случайной величины U', имеющей равномерное распределение в диапазоне (0-1). Действительно, для такого распределения p(u n ) = 1/N, D u = 1/N, и при N ® Ґ из (1.4.4) следует:

H(U') = - (log N)/N - log D u ® -.

Соответственно, разность энтропий дает дифференциальную энтропию:

h(U) = H(U) – H(U') = -p(u) log p(u) du. (1.4.6)

Дифференциальная энтропия не зависит от конкретных значений величины U:

h(U+a) = h(U), a = const,

но зависит от масштаба ее представления:

Практика анализа и обработки сигналов обычно имеет дело с сигналами в определенном интервале [a, b] их значений, при этом максимальной дифференциальной энтропией обладает равномерное распределение значений сигналов:

h(U) = -p(u) log p(u) du = log (b-a).

По мере сужения плотности распределения значение h(U) уменьшается, и в пределе при p(u) ® d (u-c), a

Знаете ли Вы, что в 1965 году два американца Пензиас (эмигрант из Германии) и Вильсон заявили, что они открыли излучение космоса. Через несколько лет им дали Нобелевскую премию, как-будто никто не знал работ Э. Регенера, измерившего температуру космического пространства с помощью запуска болометра в стратосферу в 1933 г.? Подробнее читайте в FAQ по эфирной физике.

Объединение - совокупность двух и более ансамблей дискретных, случайных событий. С объединением связаны понятия условной, безусловной, совместной и взаимной энтропии.

X Y X Y

Рис. 1. Безусловная энтропия

2. Условная энтропия - количество информации об источнике, когда известно, что принимается Y, или мера количества информации в приемнике когда известно, что передается X (рис. 2).

Рис. 2. Условная энтропия

3. Совместная энтропия - среднее количество информации на пару пе-реданных и принятых символов (рис. 3).

Рис. 3 Совместная энтропия

Рис. 4. Взаимная энтропия

Рассмотрим схему рис. 5:

()

(2)

Если в канале связи отсутствуют потери информации (нет помех, ис-кажений и т. д.), то символу x_i соответствует символ y_i . В противном случае x_i может быть принят как любой из возможных y₁ ,y₂ . y_m , с соответствующими вероятностями.

При отсутствии потерь: H(X) = H(Y). При наличии помех они уничто-жают часть информации. При этом потери информации можно определить через частные и общую условную энтропию.

Вычисление общей условной энтропии удобно производить с помощью канальных матриц ( матрицей переходных состояний).

Y X	y₁ y₂ y_m
x₁ x₂ x_m	p(y₁/x₁) p(y₂/x₁) . . . p(y_m/x₁) p(y₁/x₂) p(y₂/x₂) . . . p(y_m/x₂) p(y₁/x_m) p(y₂/x_m) . . . p(y_m/x_m)

Вероятности, расположенные на диагонали характеризует вероятность правильного приема, остальные – ложного, чем они расположены дальше от диагонали, тем они меньше. При отсутствии помех в канале связи элементы матрицы, расположенные по диагонали, равны единице, а все остальные равны нулю. Канальные матрицы всегда квадратные, т. к. количество передаваемых сигналов, равно количеству принятых, хотя вероятность прохождения отдельных сигналов может быть равна нулю.

Потери информации, вызванные действием помех, определяются с помощью условной энтропии. Для равновероятных сигналов на выходе источника общая условная энтропия вычисляется по формуле:

. (3)

Для не равновероятных сигналов на выходе источника общая условная энтропия вычисляется по формуле:

(4)

Частная условная энтропия определяет потери информации, приходящиеся на долю какого – либо конкретного сигнала (например, потери для сигнала x₁)

. (5)

При отсутствии помех вероятность получения правильного сигнала станет безусловной, а условная энтропия будет равна нулю.

Канальная матрица имеет вид, приведенный в табл. 2.

Y X	y₁ y₂ y_m
x₁ x₂ x_m	p(x₁/y₁) p(x₁/y₂) . . . p(x₁/y_m) p(x₂/y₁) p(x₂/y₂) . . . p(x₂/y_m) p(x_m/y₁) p(x_m/y₂) . . . p(x_m/y_m)

Вероятности расположения на диагонали характеризует вероятность правильной передачи, остальные – ложной. Для равновероятных сигналов на входе приемника общая условная энтропия вычисляется по формуле:

. (6)

Для не равновероятных сигналов на входе приемника общая условная энтропия вычисляется по формуле:

( 17)

Частная условная энтропия, определяющая потери, приходящиеся на долю сигнала y₁, равна:

. (8)

Решение:Для случая взаимозависимых, не равновероятных элементов энтропия равна:

P(a/b)= .

Сумма вероятности при одноименных условиях равна

Решение:Определим энтропию источника

= 0,1×0,01+0,3×0,98+0,4×0,01+0, ×2×0,01=0,301;

0,1×0+0,3×0+0,4×0,98+0,2×0,02=0,396;

0,1×0+0,3×0+0,4×0,01+0,2×0,97=0,198;

0,105+0,301+0,396+0,198=1.

При этом энтропия источника равна:

H(A)=-(0,105×log 0,105+0,301×log 0,301+0,396×log 0,396+0,198×log 0,198)=1,856 бит/симв.

бит/симв.

Полная условная энтропия равна:

Решение:Энтропия приемника равна:

Вероятности появления символов на входе приемника

;

Рис. 6. График функции плотности вероятности

При этом, выражение для энтропии можно представить в виде

(9)

Переходим к пределу:

Значение первого слагаемого определяется законом распределения и характеризует дифференциальную энтропию непрерывного источника (т. к. f(x) - плотность вероятности или дифференциальный закон распределения)

, (20)

Различные классы физических явлений и процессов подчиняются различным законам распределения. Непрерывные сигналы полностью характеризуются законами распределения (интегральным или дифференциальным). На любые реальные сигналы накладываются определенные ограничения, например: по средней мощности (нагрев аппаратуры); по мгновенной или пиковой мощности (перегрузки).

Так как дифференциальная энтропия зависит от плотности вероятности, определим, для какого закона она максимальна. Т. е. при каком распределении вероятности, сигнал заданной мощности имеет максимальную энтропию. Для нахождения максимального значения энтропии необходимо воспользоваться вариационной теоремой с использованием неопределенных множителей Лагранжа при условиях нормировки и неизменности среднего квадрата:

; .

Решив уравнения, получим симметричный нормальный закон распределения

. (11)

Если среднюю мощность не ограничивать

то получим равномерный закон распределения.

Определим дифференциальную энтропию для нормального распределения, т. е. сигнала с ограниченной средней мощностью. Полученное в результате решения вариационной задачи нормальное распределение является симметричным. Если в интеграле для дифференциальной энтропии произвести замену x = y-m_x, то интеграл не изменится, а значит, энтропия не зависит от математического ожидания и равна энтропии центрированной случайной величины.

Определим максимальное значение для энтропии:

Дифференциальная энтропия для нормального распределения равна:

(12)

Полная энтропия для нормального распределения равна:

. (13)

Если учестьчто h(x)- это математическое ожидание функции [-log₂ f(x)] от случайной величины x с плотностью f(x), то можно записать.

В соответствии с центральной предельной теоремой нормальным законам распределения подчиняются широкий класс, так называемых гауссовых случайных процессов или реальных сигналов.

Белый шум - помеха с наиболее ''зловредными" свойствами , т. е. передает максимальное количество вредящих сведений при заданной средней мощности и позволяет упростить расчеты для наихудшего случая.

Для того чтобы сигнал с ограниченной пиковой мощностью имел максимальную информативность необходимо, чтобы он имел равномерное распределение (рис. 9). Определим дифференциальную энтропию для равномерного распределения, т. е. сигнала с ограниченной пиковой мощностью. Если P-пиковая мощность, то - максимальная амплитуда. Уравнение для дифференциальной энтропии с учетом ограничений имеет вид:

Дифференциальная энтропия для равномерного распределения равна:

(14)

Полная энтропия сигнала с равномерным распределением равна:

, (15)

где m-число уровней квантования.

Определим дифференциальную энтропию для экспоненциального распределения. Это распределение широко используется для определения интенсивности отказов в радиоэлектронной аппаратуре

Полная энтропия для экспоненциального распределения равна:

. (16)

Список Литературы

1. Коганов А. В. Векторные меры сложности, энтропии, информации. “Математика. Компьютер. Образование”. Вып. 7, ч. 2, “Прогресс-Традиция”, М., 2000, с. 540 — 546

2. Яглом А. М., Яглом И. М. Вероятность и информация. М., 1957.

3. Шеннон К. Работы по теории информации и кибернетике. — М.: Изд. иностр. лит., 1963. — 830 с.

4. Волькенштейн М. В. Энтропия и информация. — М.: Наука, 1986. — 192 с.

5. Цымбал В. П. Теория информации и кодирование. — М.: Выща Школа, 1977. — 288 с.

6. Вероятностные методы в вычислительной технике. /Под ред. А.Н. Лебедева, Е.А.Чернявского. –М.: Высш. шк., 1986.

7. Седов Е.А. Взаимосвязь информации, энергии и физической энтропии в процессах управления и самоорганизации. Информация и управление. М., Наука, 1986.

Непрерывный сигнал , принимает бесконечное множество возможных значений на интервале. Вероятность появления конкретного значения, бесконечно мала, вследствие бесконечного количества их возможных значений. Пусть– плотность вероятности сигналана интервале.

(2.25)

При переходе и так как, получим

. (2.26)

. (2.27)

Значение показывает степень неопределенности различных процессов. Исходя из (2.27) значение дифференциальной энтропии может быть.

Максимальное значение достигается при нормальном распределении сигнала[]. Дляс дисперсиейзначение

. (2.28)

Пропускная способность непрерывного канала связи

Рис. 3.5. Непрерывный канал связи с ошибкой

В непрерывном канале связи (рис. 2.5), при условии действии аддитивной помехи , сигнал на выходе канала связи будет равен:

, (2.28)

то количество передаваемой информации можно определить как:

Так как при фиксированном неопределенностьопределяется исключительно, то дифференциальная энтропия помехи.

Скорость передачи информации по непрерывному каналу связи согласно (2.19) можно определить как

где количество отсчетов секунду (скорость) дискретного сигнала, с частотой дискретизации, равной верхней частоте исходного сигнала. Согласно теореме Котельникова, для точного представления сигнала, необходимо чтобы

Пропускная способность непрерывного канала связи:

. (2.29)

Минимальное значение пропускной соборности непрерывного канала связи , достигается при отсутствии автокорреляции значений помехи, что соответствует равномерному распределению энергетического спектра помехи по всему частотному диапазону пропускной способности канала связи.

Для заданных дисперсий сигнала и помехи,, согласно (2.18) получаем

Исходя из этого (2.29) можно переписать как:

, (2.30)

где – соотношение сигнал/шум.

Выражение (2.20) показывает зависимость пропускной способности непрерывного канала связи от ширины полосы пропускания сигнала и соотношения сигнал/шум. Увеличение пропускной способности канала связи может быть достигнуто за счет увеличение полосы пропускания или мощности сигнала. Однако, последнее на практике применяется крайне редко, вследствие логарифмического характера зависимости.

Если рассмотреть мощность шума через его энергетический спектр,и устремить полосу пропускания сигнала к бесконечности, получим:

так как ,

. (2.31)

Рис. 3.6. Зависимость пропускной способности непрерывного канала связи с гауссовым шумом от полосы пропускания

На рис. 2.6 представлена зависимость пропускной способности непрерывного канала связи от полосы пропускания сигнала для фиксированных и, полученное по (2.30), и предельное значение, полученное по (2.31). Характер зависимости вызван ростом мощности шума при увеличении полосы пропускания.

Графики показывают, что предельное значение пропускной способности канала связи не может превышать предельное значение, определяемое отношением мощностей сигнала и помехи.

Рис. 3.7. Структурная схема системы связи

Исходя из теоремы оптимального кодирования (2.24) для существования оптимального способа кодирования в, необходимо чтобы:

Рассматривая данный случай применительно к системе связи представленной на рис. 2.7, можно записать следующее:

. (2.32)

Формула (2.32) определяет возможность построения оптимального кода в зависимости от свойств непрерывного канала связи.

Для оценки степени согласования дискретного и непрерывного каналов связи используется показатель:

Показатель – показывает эффективность дискретного кодирования и используемой системы преобразования дискретных данных, в непрерывный сигнал.

Как отмечалось в разделе 2, для передачи сигналов в системах связи используются различные виды модуляции. В этом случае структурную схему системы связи (рис. 2.7) можно перерисовать в следующем виде (рис. 2.8).

Рис. 3.8. Структура системы связи

Рис. 3.9. Зависимость выигрыша системы модуляции от соотношения сигнал шум в канале для различных видов модуляции и отношений верхней частоты сигала к полосе пропускания канала

Для оценки качества модуляции (демодуляции) используется коэффициент

называемым выигрышем системы модуляции.

Графики зависимости от соотношения сигнал/шум в канале для различных систем модуляции и отношений верхней частоты сигнала к полосе пропускания непрерывного канала связи показаны на рис. 2.9. Пунктиром показан идеальный случай, сплошной линией значения, получаемые для реальных систем связи.

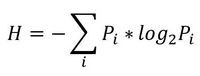
Итак, начнем с начала. Шенноном в 1963 г. было предложено понятие меры усредненной информативности испытания (непредсказуемости его исходов), которая учитывает вероятность отдельных исходов (до него был еще Хартли, но это опустим). Если энтропию измерять в битах, и взять основание 2, то получим формулу для энтропии Шеннона
, где Pi это вероятность наступления i-го исхода.

термодинамическая
алгоритмическая
информационная
дифференциальная
топологическая

Для того, чтобы немного обрисовать области применения энтропии к анализу данных, рассмотрим небольшую прикладную задачку из монографии [1] (которой нет в цифровом виде, и скорей всего не будет).

Пусть есть система, которая каждые 100 тактов переключается между несколькими состояниями и порождает сигнал x (рисунок 1.5), характеристики которого изменяются при переходе. Но какие — нам не известно.

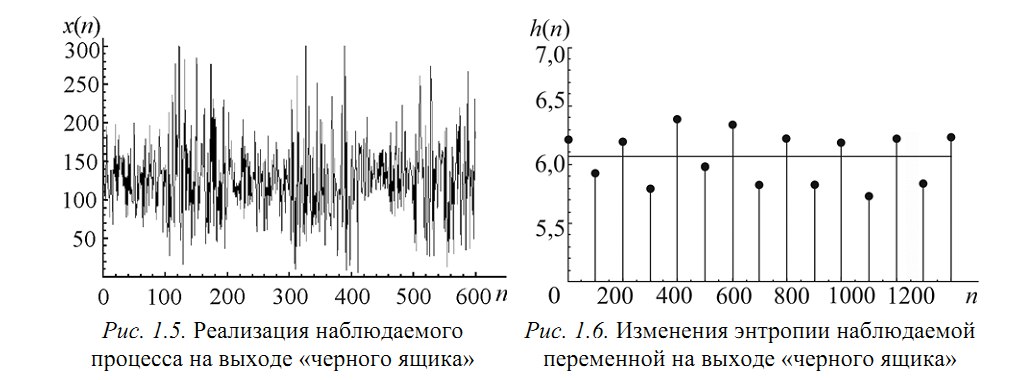
Теперь еще про одно занятное свойство энтропии — она позволяет оценить степень связности нескольких процессов. При наличии у них одинаковых источников мы говорим, что процессы связаны (например, если землетрясение фиксируют в разных точках Земли, то основная составляющая сигнала на датчиках общая). В таких случаях обычно применяют корреляционный анализ, однако он хорошо работает только для выявления линейных связей. В случае же нелинейных (порожденных временными задержками, например) предлагаем пользоваться энтропией.

Рассмотрим модель из 5ти скрытых переменных(их энтропия показана на рисунке ниже слева) и 3х наблюдаемых, которые генерируются как линейная сумма скрытых, взятых с временными сдвигами по схеме, показанной ниже справа. Числа-это коэффициенты и временные сдвиги (в отсчетах).

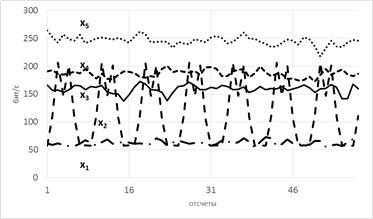
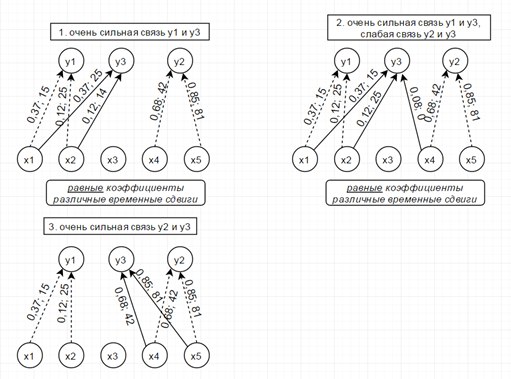
Так вот, фишка в том, что энтропия связных процессов сближается при усилении их связи. Черт побери, как это красиво-то!

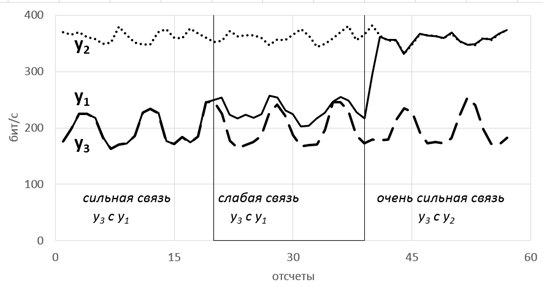
Такие радости позволяют вытащить практически из любых самых странных и хаотичных сигналов (особенно полезно в экономике и аналитике) дополнительные сведения. Мы их вытаскивали из электроэнцефалограммы, считая модную нынче Sample Entropy и вот какие картинки получили.

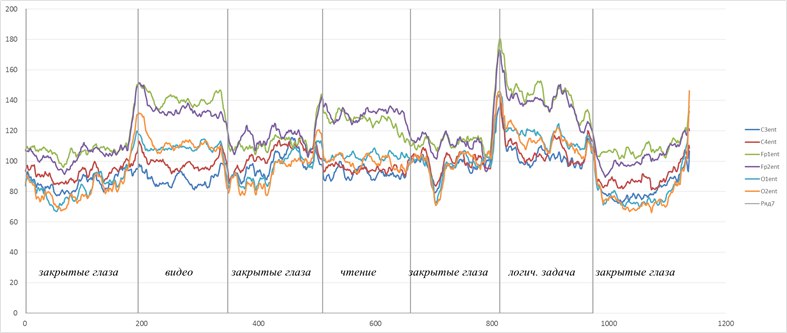
Можно видеть, что скачки энтропии соответствуют смене этапов эксперимента. На эту тему есть пара статей и уже защищена магистерская, так что если кому будут интересны подробности — с радостью поделюсь. А так по миру по энтропии ЭЭГ ищут уже давно разные вещи — стадии наркоза, сна, болезни Альцгеймера и Паркинсона, эффективность лечения от эпилепсии считают и тд. Но повторюсь-зачастую расчеты ведутся без учета поправочных коэффициентов и это грустно, так как воспроизводимость исследований под большим вопросом (что критично для науки, так то).

Резюмируя, остановлюсь на универсальности энтропийного аппарата и его действительной эффективности, если подходить ко всему с учетом подводных камней. Надеюсь, что после прочтения у вас зародится зерно уважения к великой и могучей силе Энтропии.

Концепции информации и энтропии имеют глубокие связи друг с другом, но, несмотря на это, разработка теорий в статистической механике и теории информации заняла много лет, чтобы сделать их соответствующими друг другу. Ср. тж.

Содержание

Формальные определения

Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле:

$<\displaystyle H(x)=-\sum _<i=1> ^p(i)\log _p(i)>$

Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей.

где K — константа (и в действительности нужна только для выбора единиц измерения).

$<\displaystyle H_ (<\mathcal <S>>)=-\sum _^p_\log _p_>$

Условной энтропией первого порядка (аналогично для вероятности появления одной буквы после другой (т.е. вероятности двухбуквенных сочетаний):

$<\displaystyle H_<1> (<\mathcal <S>>)=-\sum _p_\sum _\ p_(j)\log _p_(j)>$

где " width="" height="" />
— это состояние, зависящее от предшествующего символа, и (j)>" width="" height="" />
— это вероятность " width="" height="" />
, при условии, что " width="" height="" />
был предыдущим символом.

Так, для русского алфавита без буквы « [1]

Через частную и общую условные энтропии полностью описываются информационные потери при передаче данных в канале с помехами. Для этого применяются т.н. канальные матрицы. Так, для описания потерь со стороны источника (т.е. известен посланный сигнал), рассматривают условную вероятность |a_)>" width="" height="" />
получения приёмником символа >" width="" height="" />
при условии, что был отправлен символ >" width="" height="" />
. При этом канальная матрица имеет следующий вид:

$<\displaystyle \displaystyle b_>$
$<\displaystyle \displaystyle b_>$
. $<\displaystyle \displaystyle b_<j>>$
. $<\displaystyle \displaystyle b_>$

$<\displaystyle \displaystyle a_>$
$<\displaystyle \displaystyle p(b_|a_)>$
$<\displaystyle \displaystyle p(b_|a_)>$
. $<\displaystyle \displaystyle p(b_<j>|a_)>$
. $<\displaystyle \displaystyle p(b_|a_)>$

$<\displaystyle \displaystyle a_>$
$<\displaystyle \displaystyle p(b_|a_)>$
$<\displaystyle \displaystyle p(b_|a_)>$
. $<\displaystyle \displaystyle p(b_<j>|a_)>$
. $<\displaystyle \displaystyle p(b_|a_)>$

. . . . . . .

$<\displaystyle \displaystyle a_>$
$<\displaystyle \displaystyle p(b_|a_)>$
$<\displaystyle \displaystyle p(b_|a_)>$
. $<\displaystyle \displaystyle p(b_<j>|a_)>$
. $<\displaystyle \displaystyle p(b_|a_)>$

. . . . . . .

$<\displaystyle \displaystyle a_>$
$<\displaystyle \displaystyle p(b_|a_)>$
$<\displaystyle \displaystyle p(b_|a_)>$
. $<\displaystyle \displaystyle p(b_<j>|a_)>$
. $<\displaystyle \displaystyle p(b_|a_)>$

$<\displaystyle \displaystyle p(b_<j> Очевидно, вероятности, расположенные по диагонали описывают вероятность правильного приёма, а сумма всех элементов столбца даст вероятность появления соответствующего символа на стороне приёмника — )>$
. Потери, приходящиеся на предаваемый сигнал >" width="" height="" />
, описываются через частную условную энтропию:

$<\displaystyle H(B|a_ )=-\sum _^p(b_|a_)\log _p(b_|a_)>$

Для вычисления потерь при передаче всех сигналов используется общая условная энтропия:

$<\displaystyle \displaystyle H(B|A)=\sum _ p(a_)H(B|a_)>$

" width="" height="" />
означает энтропию со стороны источника, аналогично рассматривается " width="" height="" />
— энтропия со стороны приёмника: вместо |a_)>" width="" height="" />
всюду указывается |b_)>" width="" height="" />
(суммируя элементы строки можно получить )>" width="" height="" />
, а элементы диагонали означают вероятность того, что был отправлен именно тот символ, который получен, т.е. вероятность правильной передачи).

Взаимная энтропия

$<\displaystyle \displaystyle p(a_ Взаимосязь переданных и полученных сигналов описывается вероятностями совместных событий b_)>$
, и для полного описания характеристик канала требуется только одна матрица:

$<\displaystyle \displaystyle p(a_b_)>$
$<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$

$<\displaystyle \displaystyle p(a_b_)>$
$<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$

… … … … … …

$<\displaystyle \displaystyle p(a_b_)>$
$<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$

… … … … … …

$<\displaystyle \displaystyle p(a_b_)>$
$<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$
… $<\displaystyle \displaystyle p(a_b_)>$

Для более общего случая, когда описывается не канал, а просто взаимодействующие системы, матрица необязательно должна быть квадратной. Очевидно, сумма всех элементов столбца с номером " width="" height="" />
даст )>" width="" height="" />
, сумма строки с номером " width="" height="" />
есть )>" width="" height="" />
, а сумма всех элементов матрицы равна 1. Совместная вероятность b_)>" width="" height="" />
событий >" width="" height="" />
и >" width="" height="" />
вычисляется как произведение исходной и условной вероятности,

$<\displaystyle \displaystyle p(a_ b_)=p(a_)p(b_|a_)=p(b_)p(a_|b_).>$

Условные вероятности производятся по формуле Байеса. Таким образом имеются все данные для вычисления энтропий источника и приёмника:

$<\displaystyle H(A)=-\sum _ \left(\sum _p(a_b_)\log \sum _p(a_b_)\right)>$
\left(\sum _p(a_b_)\log \sum _p(a_b_)\right)>" width="" height="" />

Взаимная энтропия вычисляется последовательным суммированием по строкам (или по столбцам) всех вероятностей матрицы, умноженных на их логарифм:

$<\displaystyle \displaystyle H(AB)=-\sum _ \sum _p(a_b_)\log p(a_b_)>$

Единица измерения — бит/два символа, это объясняется тем, что взаимная энтропия описывает неопределённость на пару символов — отправленного и полученного. Путём несложных преобразований также получаем

$<\displaystyle \displaystyle H(AB)=H(A)+H(B|A)=H(B)+H(A|B).> $

Взаимная энтропия обладает свойством информационной полноты — из неё можно получить все рассматриваемые величины.

Свойства

Важно помнить, что энтропия является количеством, определённым в контексте вероятностной модели для . Так, к примеру, опытным путём можно установить, что энтропия английского текста равна 1,5 Альтернативное определение

Другим способом определения функции энтропии H является доказательство, что H однозначно определена (как указано ранее), если и только если H удовлетворяет пунктам 1)—3):

$<\displaystyle \in > 1) H(p1, …, pn) определена и непрерывна для всех p1, …, pn, где pi$
[0,1] для всех i = 1, …, n и p₁ + … + p_n = 1. (Заметьте, что эта функция зависит только от распределения вероятностей, а не от алфавита.)

2) Для целых положительных n, должно выполняться следующее неравенство:

3) Для целых положительных b_i, где b₁ + … + b_n = n, должно выполняться равенство:

$<\displaystyle H\left( >,\ldots ,>\right)=H\left(>>,\ldots ,>>\right)+\sum _^>>H\left(>>,\ldots ,>>\right).>$

Эффективность

Из этого следует, что эффективность исходного алфавита с n символами может быть определена просто как равная его n-арной энтропии.

Энтропия ограничивает максимально возможное сжатие без потерь (или почти без потерь), которое может быть реализовано при использовании теоретически — История

См. также

Эта статья содержит материал из статьи Информационная энтропия русской Википедии.

Читайте также:


Необходимо ли иметь в жизни убеждения сочинение с аргументами из литературы

Итоговое сочинение война судьба человека

Къара кюбюр сочинение на карачаевском языке

Какими качествами должен обладать тот от чьего профессионализма зависит жизнь пациентов сочинение

Сочинение на тему весенняя прогулка

$<\displaystyle \displaystyle b_>$	$<\displaystyle \displaystyle b_>$	.	$<\displaystyle \displaystyle b_<j>>$	.	$<\displaystyle \displaystyle b_>$
$<\displaystyle \displaystyle a_>$	$<\displaystyle \displaystyle p(b_\|a_)>$	$<\displaystyle \displaystyle p(b_\|a_)>$	.	$<\displaystyle \displaystyle p(b_<j>\|a_)>$	.	$<\displaystyle \displaystyle p(b_\|a_)>$
$<\displaystyle \displaystyle a_>$	$<\displaystyle \displaystyle p(b_\|a_)>$	$<\displaystyle \displaystyle p(b_\|a_)>$	.	$<\displaystyle \displaystyle p(b_<j>\|a_)>$	.	$<\displaystyle \displaystyle p(b_\|a_)>$
.	.	.	.	.	.	.
$<\displaystyle \displaystyle a_>$	$<\displaystyle \displaystyle p(b_\|a_)>$	$<\displaystyle \displaystyle p(b_\|a_)>$	.	$<\displaystyle \displaystyle p(b_<j>\|a_)>$	.	$<\displaystyle \displaystyle p(b_\|a_)>$
.	.	.	.	.	.	.
$<\displaystyle \displaystyle a_>$	$<\displaystyle \displaystyle p(b_\|a_)>$	$<\displaystyle \displaystyle p(b_\|a_)>$	.	$<\displaystyle \displaystyle p(b_<j>\|a_)>$	.	$<\displaystyle \displaystyle p(b_\|a_)>$

$<\displaystyle \displaystyle p(a_b_)>$	$<\displaystyle \displaystyle p(a_b_)>$	…	$<\displaystyle \displaystyle p(a_<i>b_)>$	…	$<\displaystyle \displaystyle p(a_b_)>$
$<\displaystyle \displaystyle p(a_b_)>$	$<\displaystyle \displaystyle p(a_b_)>$	…	$<\displaystyle \displaystyle p(a_b_)>$	…	$<\displaystyle \displaystyle p(a_b_)>$
…	…	…	…	…	…
$<\displaystyle \displaystyle p(a_<i>b_)>$	$<\displaystyle \displaystyle p(a_<i>b_)>$	…	$<\displaystyle \displaystyle p(a_<i>b_)>$	…	$<\displaystyle \displaystyle p(a_<i>b_)>$
…	…	…	…	…	…
$<\displaystyle \displaystyle p(a_b_)>$	$<\displaystyle \displaystyle p(a_b_)>$	…	$<\displaystyle \displaystyle p(a_b_)>$	…	$<\displaystyle \displaystyle p(a_b_)>$