Загадочные графики тригонометрических функций реферат
Обновлено: 06.07.2024
Цель работы: изучение тригонометрических функций, их свойств
и графиков.
Гипотеза: изучение тригонометрических функций будет более эффективным, в том случае когда:
1) перед введением тригонометрических функций проведена достаточно широкая пропедевтическая работа с числовой окружностью;
2) числовая окружность рассматривается не только как самостоятельный объект, но и как элемент декартовой системы координат;
3) построение графиков осуществляется после исследования свойств тригонометрических функций, исходя из анализа поведения функции на числовой окружности;
Содержание работы
Раздел 1. Тригонометрические функции и их графики……………7
1.1 Обобщение понятия угла. Числовая окружность на координатной
плоскости………………………………………………………….…………. 7
Синус и косинус. Тангенс и котангенс………………………. ….….……..10
Тригонометрические функции углового аргумента……. ………. …..…..11
Четность и нечетность тригонометрических функций……….….………. 13
1.5 Основные тригонометрические тождества…………………………….……13
Основные тригонометрические формулы…………………………………15
Формулы приведения……………………………………………………15
Теоремы сложения……………………………………………………….16
Формулы двойного аргумента. Формулы половинного аргумента.18
Преобразование суммы и разности тригонометрических функций
в произведение и обратные преобразования………………..……….20
1.7 Области определения и множества значений тригонометрических
функций…………………………………………………………………..…..22
Периодичность тригонометрических функций…………………………….22
Интервалы знакопостоянства тригонометрических функций……………23
1.10 Графики тригонометрических функций………………………………….24
1.10.1 График функции и ее свойства……………………………….24
1.10.2 График функции ……………………………………………….25
1.10.3 График функции …………………………………. 26
1.11 Гармонические колебания…………………………………………………27
Раздел 2. Методы решения тригонометрических уравнений……29
2.1 Тригонометрические уравнения…………………………………………. 29
2.2 Уравнения, сводимые к алгебраическим………………………………….31
2.3 Однородные уравнения…………………………………………………. …..32
2.4 Уравнения, решаемые методом разложения на множители……………..33
2.5 Уравнения, решаемые методом введения дополнительного угла……….34
2.6 Метод универсальной подстановки…………………………………………35
2.7 Метод оценок…………………………………………………………………35
2.8 Уравнения, решаемые понижением степени уравнения…………………..37
2.9 Уравнения, решаемые преобразованием тригонометрических
произведений в сумму или разность………………………………………. 37
2.10 Уравнения, решаемые преобразованием тригонометрических сумм
(разностей) в произведение…………………………………………………37
Раздел3. Примеры решения тестовых заданий……………………39
Файлы: 1 файл
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ.docx
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
«Гомельский государственный университет
Кафедра Высшей математики
Тригонометрические функции и их графики
студент группы М-51 __________ Е.В.Марухленко
_______________________ _____________ ____________
ученая степень, звание подпись И.О.Ф.
Курсовая работа 43 страницы, 30 рисунков, 6 таблиц, 12 источников.
Ключевые слова: курсовая работа, тригонометрические функции, свойства, графики, тригонометрические уравнения, методы решения, примеры решения тестовых заданий.
Объект исследования: тригонометрические функции и их графики
Цель работы: изучение тригонометрических функций, их свойств
Раздел 1. Тригонометрические функции и их графики……………7
1.1 Обобщение понятия угла. Числовая окружность на координатной
- Синус и косинус. Тангенс и котангенс………………………. ….….……..1 0
- Тригонометрические функции углового аргумента……. ………. …..…..11
- Четность и нечетность тригонометрических функций……….….………. 13
- Основные тригонометрические формулы…………………………………15
- Формулы приведения…………………………………………………… 15
- Теоремы сложения………………………………………………………. 16
- Формулы двойного аргумента. Формулы половинного аргумента.18
- Преобразование суммы и разности тригонометрических функций
в произведение и обратные преобразования………………..……….20
1.7 Области определения и множества значений тригонометрических
- Периодичность тригонометрических функций…………………………….22
- Интервалы знакопостоянства тригонометрических функций……………23
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
- Синус угла b называется отношением AB/OB (отношение противоположного катетера к гипотенузе);
- Козин угла b называется отношением OA/OB (отношение смежного катетера к гипотенузе);
- Касательная угла b называется отношением AB/OA (отношение противоположного катетера к соседнему катетеру);
- Катангензис угла b называется отношением OA/AB (отношение смежного катетера к противоположному катетеру);
- Секанс угла b называется отношением ОВ/ОА (отношение гипотенузы к соседнему катетеру);
- Угол cosecansome b называется отношением OV/AB (отношение гипотенузы к контркатетеру).
- Сложные синусоидальные и косинусоидальные значения, в отличие от реальных, могут принимать любое количество значений модуля;
- Все нули сложного синуса и косинуса лежат на оси материала.
- Функция y=sin х периодическая с главным периодом T = 2π, т.е.
- Функция y = sin х непрерывна на промежутке (- ∞ ; + ∞).
- График функции пересекает ось Ох при х = π k , k ∈ Z .
- Промежутки знакопостоянства:
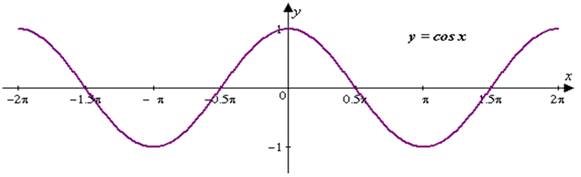
- Функция y= cos х четная, так как cos(−х) = cos х.
- Функция y=cosх периодическая с главным периодом T = 2π, т.е. cos(х+2π)= cosх.
- Функция y=cosх непрерывна на промежутке (- ∞ ; + ∞).
- График функции пересекает ось Ох при х= +π k , k ∈ Z .
- Промежутки знакопостоянства:
- Функция y=cosх возрастает на каждом из промежутков [−π+2π k ;2π k ], k ∈Z , и убывает на каждом из промежутков [ 2π k ;π+2π k ], k ∈ Z.
- Минимум функции при х=π+2π k , k ∈ Z , а максимум при х=2π k , k ∈ Z .
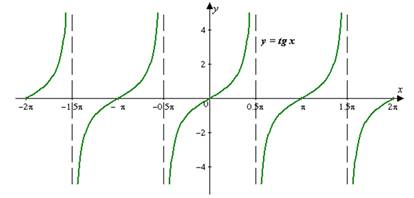
- Функция y= tgх нечетная, так как tg(−х)=−tg х.
- Функция y=tgх периодическая с главным периодом равным T = π, т.е. tg(х+π)=tg(х).
- Функция y=tg х непрерывна на каждом интервале (− +π k ; +π k ), k ∈ Z
- График функции пересекает ось Ох при х=π k , k ∈ Z.
- Промежутки знакопостоянства:
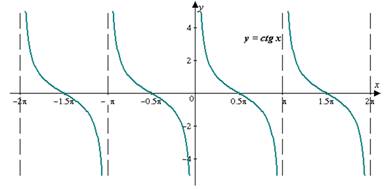
- Функция y=ctgх нечетная, так как ctg(−х)=−ctg х.
- Функция y=ctgх периодическая с главным периодом равным T = π, т.е. ctg(х+π)=ctg(х).
- Функция y=ctgх непрерывна на каждом интервале (πn; π+π k ), где k ∈ Z. .
- График функции пересекает ось Ох при х= +π k , k ∈ Z .
- Промежутки знакопостоянства:
- Функция y=ctg x убывает на каждом интервале (0+π k ; π+π k ), k ∈ Z.
- Алгебра и начала математического анализа: Учеб для 10-11 кл.общеобразоват. организаций / А.Н.Колмогоров, А.М.Абрамов, Ю.П.Дудницин и др. под редакцией А.Н.Колмогорова- М. Просвещение, 2018.
1.10 Графики тригонометрических функций………………………………….24
1.10.1 График функции и ее свойства……………………………….24
1.10.3 График функции …………………………………. 26
1.11 Гармонические колебания…………………………………………………27
Раздел 2. Методы решения тригонометрических уравнений……29
2.1 Тригонометрические уравнения…………………………………………. 29
2.2 Уравнения, сводимые к алгебраическим………………………………….31
2.4 Уравнения, решаемые методом разложения на множители……………..33
2.5 Уравнения, решаемые методом введения дополнительного угла……….34
2.6 Метод универсальной подстановки…………………………………………35
2.8 Уравнения, решаемые понижением степени уравнения…………………..37
2.9 Уравнения, решаемые преобразованием тригонометрических
произведений в сумму или разность………………………………………. 37
2.10 Уравнения, решаемые преобразованием тригонометрических сумм
(разностей) в произведение……………………………………………… …37
Раздел3. Примеры решения тестовых заданий……………………39
Список используемых источников………………………………….43
Потребность в измерении углов возникла так же давно, как и потребность в измерении расстояний. Одним из стимулов развития тригонометрии была необходимость определения времени, определения положения корабля в открытом море или каравана в пустыне.
Изучая зависимость между сторонами и углами треугольника, древние нашли способы вычислений различных элементов треугольника.
Некоторыми знаниями тригонометрии владели ученые Древнего Вавилона. Об этом свидетельствует тот факт, что вавилоняне умели предсказывать солнечные и лунные затмения. На одной из глиняных табличек Древнего Вавилона (2 тыс. лет до н. э.) решается задача, в которой по известному диаметру круга и высоте сегмента вычисляется длина хорды,
что соответствует установлению связи между синусом и косинусом.
Древнегреческие ученые владели методами решения прямоугольных треугольников. Астроном и математик Гиппарх (II в. до н. э.) составил таблицы хорд— первые тригонометрические таблицы.
. Эти сведения по тригонометрии использовались главным образом для решения задач практической астрономии, для определения не доступных расстояний.
Дальнейшее развитие тригонометрии осуществили ученые Индии и Ближнего и Среднего Востока. Ими были введены синус, косинус, тангенс, котангенс, положено начало радианной мере угла. Тригонометрические знания, накопленные арабскими математиками, достигли такого уровня, что тригонометрию стали считать отдельным разделом математики.
Впервые обозначать синус и косинус знаками и стал
И. Бернулли в письме 1739 г. к Эйлеру. Эйлер принял эти обозначения и систематически применял их.
После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее, проще.
В настоящее время изучению тригонометрических функций именно как функций числового аргумента уделяется большое внимание в школьном курсе алгебры и начал анализа. Существует несколько различных подходов к преподаванию данной темы в школьном курсе. Тригонометрические функции представляют собой наиболее удобное и наглядное средство для изучения всех свойств функций (до применения производной), а в особенности такого свойства многих природных процессов как периодичность. Поэтому их изучению следует уделить пристальное внимание, что обуславливает актуальность изучения исследуемой работы.
Цель работы: изучение тригонометрических функций, их свойств
Гипотеза: изучение тригонометрических функций будет более эффективным, в том случае когда:
1) перед введением тригонометрических функций проведена достаточно широкая пропедевтическая работа с числовой окружностью;
2) числовая окружность рассматривается не только как самостоятельный объект, но и как элемент декартовой системы координат;
3) построение графиков осуществляется после исследования свойств тригонометрических функций, исходя из анализа поведения функции на числовой окружности;
4) Выделить основы формирования умений, необходимых для решения тригонометрических уравнений.
Для решения проблемы исследования, проверки достоверности гипотезы и достижения цели реализуются следующие задачи:
1) исследование научно- методической литературы по этой теме;
2) проведение логико-дидактического анализа изложения этой темы в современных учебных пособиях;
III -я региональная научно-практическая конференция
для старшеклассников школ Челябинской области
Тригонометрия в нашей жизни
Автор: Суворова Анастасия, 10 класса
МОУ Кременкульской СОШ
Научный руководитель:
Грязнова Татьяна Александровна,
МОУ Кременкульской СОШ
с. Долгодеревенское, 2019
Актуальность:
Данная тема является одной из самых актуальных. Она находит широкое применение в разных разделах математики, и других областях науки, а также тесно связана с деятельностью человека. Имеет теоретическую и практическую значимость.
Объект исследования: Тригонометрия.
Предмет исследования: Графики тригонометрической функции
Узнать о способах применения графиков тригонометрических функции в жизни человека.
Составить историческую справку о графиках тригонометрических функций.
Описать применение графиков тригонометрических функций в окружающем нас мире и различных отраслях.
Вывести свой биоритм жизни.
Изготовить демонстрационную модель движения графика синуса.
Графики тригонометрических функций широко применяются человеком, начиная с древности, и заканчивая настоящим временем.
Теоретическая часть
Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы.
Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия, в акустике, в оптике, в анализе финансовых рынков, в статистике, в биологии, в медицинской визуализации, например, компьютерной томографии и ультразвук, в химии (Приложение 1, рис.1), в сейсмологии (Приложение 1, рис.2), в метеорологии, в океанографии (Приложение 1, рис.3), в архитектуре (Приложение 1, рис.4), в экономике, в компьютерной графике, в кристаллографии (Приложение 1, рис.5) и многих других областях.
Часто с синусами и косинусами приходится сталкиваться геодезистам. Они имеют специальные инструменты для точного измерения углов. При помощи синусов и косинусов углы можно превратить в длины или координаты точек на земной поверхности.
История возникновения
Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая (Приложение 2, рис.1) . 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.
В общем, можно сказать, что тригонометрия использовалась для:
· точного определения времени суток; (Приложение 2, рис. 3)
· вычисления будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны;
· нахождения географических координат текущего места;
· вычисления расстояния между городами с известными географическими координатами.
Гномон— древнейший астрономический инструмент, вертикальный предмет (стела, колонна, шест), позволяющий по наименьшей длине его тени (в полдень)
определить угловую высоту солнца. Так, под котангенсом понималась длина тени от вертикального гномонавысотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке слева)
Тригонометри́ческие фу́нкции (Приложение 2, рис. 5) — элементарные функции, которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла (дуги) в круге). Эти функции нашли широчайшее применение в самых разных областях науки. Впоследствии определение тригонометрических функций было расширено, их аргументом теперь может быть произвольное вещественное или даже комплексное число. Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
Синус и косинус относятся к прямым тригонометрическим функциям.
В настоящее время график синуса можно встретить в следующих моментах нашей жизни.
Архитектура
Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений
рисунков проходило именно с помощью геометрии. Но теоретические данные мало что значат. Хочу привести пример на построение одной скульптуры французского мастера Золотого века искусства.
Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой.
Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности. Велось множество расчетов, чтобы фигура с большой высоты смотрелась пропорционально. В основном они были основаны на методе визирования, то есть приблизительного измерения, на глаз. Однако коэффициент разности тех или иных пропорций позволили сделать фигуру приближенной к идеалу. Таким образом, зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы (то же самое мы можем сделать и с нижней точкой зрения), тем самым найдем точку зрения
Ситуация меняется, так как статую поднимают на высоту, поэтому расстояние от верхушки статуи до глаз человека увеличивается, следовательно и синус угла падения увеличивается. Сравнив изменения расстояния от верхушки статуи до земли в первом и во втором случаи, можно найти коэффициент пропорциональности. Впоследствии мы получим чертеж, а потом скульптуру, при поднятии которой зрительно фигура будет приближена к идеалу.
Медицина и биология.
Модель биоритмов (Приложение 2, рис.11), которые в свою очередь подразумевают цикличность процессов в живом организме можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (кол-во дней).
Формула сердца. В результате исследования, проведенного студентом иранского университета Шираз Вахидом-Резой Аббаси, медики впервые получили возможность упорядочить информацию, относящуюся к электрической активности сердца или, другими словами, электрокардиографии.
Формула представляет собой комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии. Как утверждают медики, эта формула в значительной степени облегчает процесс описания основных параметров, деятельности сердца, ускоряя, тем самым, постановку диагноза и начало собственно лечения.
Также тригонометрия помогает нашему мозгу определять расстояния до объектов.
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения. Строго говоря, идея "измерения углов" не является новой. Еще художники Древнего Китая рисовали удаленные объекты выше в поле зрения, несколько пренебрегая законами перспективы. Сформулировал теорию определения расстояния по оценке углов арабский ученый XI века Альхазен. После долгого забвения в середине прошлого столетия идею реанимировал психолог Джеймс Гибсон (James Gibson), строивший свои выводы на основе опыта работы с пилотами военной авиации. Однако после того о теории вновь позабыли.
Движение рыб в воде и полёт птиц (Приложение 2, рис. 10) происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx.
Измерительные работы
Собрала для вас похожие темы рефератов, посмотрите, почитайте:
Введение
Я заинтересовался этой темой, потому что хотел узнать больше о тригонометрии и особенно о ее истории.
Я поставил перед собой цель: определить на основе отобранного материала, где тригонометрия, за исключением школьного курса, встречается в решении проблем и идентичностей.
Прочитав литературу, я узнал, что тригонометрические вычисления используются практически во всех областях геометрии, физики и технологии. Большое значение имеет метод триангуляции, который может быть использован для измерения расстояний до далеких звезд в астрономии, между географическими достопримечательностями для управления спутниковыми навигационными системами.
Также стоит отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансового рынка, электроника, теория вероятности, статистика, биология, медицина (в том числе ультразвук и компьютерная томография), фармация, химия, теория чисел (и), как следствие криптографии), сейсмологии, метеорологии, океанографии, картографии, многих областях физики, топографии и геодезии, архитектуры, фонетики, экономики, электротехники, машиностроения, компьютерной графики, кристаллографии, а также я узнал много нового, чего раньше не знал.
По истории тригонометрии
Тригонометрия — греческое слово и буквально означает измерение треугольников (Триггунон — треугольник и измерение Метрю).
В этом случае под измерением треугольников следует понимать треугольное решение, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, но также и задачи планаметрии, стереометрии, астрономии и другие даны задачам решения треугольников.
Появление тригонометрии связано с астрономией и строительством.
Хотя название науки появилось сравнительно недавно, многие понятия и факты, связанные с тригонометрией, были известны уже две тысячи лет назад.
Решения для треугольников, основанные на зависимостях между сторонами и углами треугольника, были впервые найдены древнегреческими астрономами Гиппархом (II в. до н.э.) и Клавдием Птолемеем (II в. н.э.). Позже отношения между сторонами треугольника и его углами стали называться тригонометрическими функциями.
В долгой истории существует понятие синуса. Фактически, различные соотношения сечений треугольника и круга (а по существу, и тригонометрические функции) встречаются уже в III в. до н.э. в трудах великих математиков Древней Греции — Евклида, Архимеда, Аполлонии Пергусской. В римский период эти отношения систематически изучались Менелаем (I в. н.э.), хотя конкретное название им не давалось. Современный синус a, например, изучался как полуаккорд, на котором центральный угол лежит в размере a, или как двухдуговой аккорд.
Уже в IV-V веке в астрономических трудах великого индийского ученого Ариабхаты, чье имя было дано первому индийскому спутнику Земли, существовал особый термин. Он назвал отрезок АМ (рис. 1) аргаджива (арга — половина, джива — луковая струна, которая напоминает аккорд). Позже появилось более короткое имя Джива. Арабские математики в IX в. заменили это слово на арабское слово jib (выпуклость). В переводе арабских математических текстов в этом столетии он был заменен на латинский синус (синус — кривизна, изгиб).
Касательные появились в связи с решением задачи определения длины тени. Тангент (как и кокангент) был введен в X. столетие арабский математик Абу-л-Вафа, который создал первые таблицы для нахождения тангенса и кокангента. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенты были заново открыты только в XIV веке немецким математиком и астрономом Реджимонтаном (1467 г.). Он доказал теорему о тангенте. Regimontan также сделал подробные тригонометрические таблицы, благодаря его работам плоские и сферические тригонометрии стали отдельной дисциплиной в Европе.
Дальнейшее развитие тригонометрии состоялось в трудах выдающегося астронома Николая Коперника (1473-1543) — создателя мировой гелиоцентрической системы Тихо Браге (1546-1601) и Иоганна Кеплера (1571-1630), а также в трудах математика Франсуа Виета (1540-1603), который полностью решил задачу определения всех элементов плоского или сферического треугольника на три даты.
Долгое время тригонометрия была чисто геометрической. Факты, которые мы сейчас формулируем в виде тригонометрических функций, были сформулированы и доказаны с помощью геометрических концепций и высказываний. Так было уже в средние века, хотя иногда использовались аналитические методы, особенно после появления логарифмов. Пожалуй, наибольший стимул для развития тригонометрии возник в связи с решением астрономических задач, представлявших большой практический интерес (например, для решения задач определения положения корабля, прогнозирования отключения электроэнергии и т.д.). Астрономов интересовали отношения между сторонами и углами сферических треугольников. И надо сказать, что математики древнего мира успешно справились с поставленными задачами.
С XVII века тригонометрические функции стали использоваться для решения уравнений, задач механики, оптики, электротехники, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, изучения переменного тока и др. Поэтому тригонометрические функции были всесторонне и глубоко исследованы и приобрели значение для всей математики.
Аналитическая теория тригонометрических функций была разработана в основном Леонардом Эйлером (1707-1783), выдающимся математиком XVIII века, членом Санкт-Петербургской Академии наук. Большое научное наследие Эйлера включает в себя блестящие результаты, связанные с математическим анализом, геометрией, теорией чисел, механикой и другими математическими приложениями. Именно Эйлер первым ввел известные определения тригонометрических функций, начал рассматривать функции любого угла, и получил формулы редукции. По словам Эйлера, тригонометрия получила форму расчета: различные факты стали доказываться формальным применением формул тригонометрии, доказательства стали намного компактнее.
Таким образом, тригонометрия, зародившаяся как наука о разрешении треугольников, со временем переросла в науку о тригонометрических функциях.
Тригонометрические функции
Элементарные функции, которые исторически возникали при взгляде на прямоугольные треугольники и выражают зависимость сторон этих треугольников от острых углов гипотенузы (или, эквивалентно, зависимость аккордов и высоты от центрального угла в круге). Эти функции нашли самое широкое применение в различных областях науки. В результате было расширено определение тригонометрических функций, и их аргументом теперь может быть любое реальное или даже сложное число.
Наука, изучающая свойства тригонометрических функций, называется тригонометрией.
Ссылка на тригонометрические функции:
Во-первых, прямые тригонометрические функции:
Во-вторых, противоположные тригонометрические функции:
В-третьих, производные тригонометрические функции:
В западной литературе загар х, кроватка х, цхх называются загаром, кроватка х, цхх.
В дополнение к этим шести, существуют также некоторые редко используемые тригонометрические функции (верна и т.д.) и обратные тригонометрические функции (арксин, аркозин и т.д.), которые рассматриваются в отдельных статьях.
Синусоидальный и косинусоидальный вещественные аргументы являются периодически непрерывными и бесконечно дифференцируемыми вещественными функциями.
Остальные четыре функции на реальной оси также являются материально значимыми, периодическими и бесконечно различимыми в областях определения, но не непрерывными.
Тангенты и секанты имеют паузы второго поколения на ±rp, в то время как катангенсы и секанты имеют паузы на ±rp.
Геометрическое определение
Обычно тригонометрические функции определяются геометрически. Укажем декартовую систему координат на плоскости и сформируем окружность радиусом R, центр которой находится в начале координат O. Измеряем углы как вращения от положительного направления оси абсциссы к акустическому пучку. Направление против часовой стрелки считается положительным, направление по часовой — отрицательным. Если мы обозначим абсциссой точку B с xB, то мы обозначим ординату с yB.
Понятно, что значения тригонометрических функций не зависят от радиуса окружности R из-за свойств подобных фигур.
Следует также отметить, что этот радиус часто принимается равным значению одного сечения.
Исходя из этого, синус является просто ординатой yB, а косинус — абсциссой xB.
Если b является вещественным числом, то в математическом анализе синус b называется угловым синусом, радиан которого равен b, аналогично другим тригонометрическим функциям.
Рассмотрим графическое изображение этого явления на рисунке 3.
Определение тригонометрических функций как решений дифференциальных уравнений, уравнений функций и по ряду
Во многих учебниках элементарной геометрии тригонометрические функции острого угла до сих пор определялись как отношения сторон прямоугольного треугольника. Пусть ОАБ будет треугольником с углом b.
Ну, тогда:
После того, как мы построили систему координат с началом в точке О, изменили направление оси абсциссы вдоль ОА и, при необходимости, ориентацию треугольника (перевернув его) так, чтобы он лежал в первой четверти системы координат, а затем построили окружность с радиусом, равным гипотенусе, сразу замечаем, что такое определение функций приводит к тому же результату, что и предыдущее.
На основании геометрии и свойств предельных значений можно доказать, что производная синуса равна косинусу, а производная косинуса равна минус синус. Затем можно использовать преимущества теории рядов Тейлора и представить синус и косинус как сумму степенных рядов.
Самые простые личности
Тригонометрические тождества — это математические выражения для тригонометрических функций, которые выполняются по всем значениям аргумента (из общего диапазона определений).
Поскольку синус и косинус являются ординатой и абсциссой точки, соответствующей единичной окружности впадин, то в соответствии с уравнением единичной окружности или пифагорейской теоремой.
Это соотношение называется базовой тригонометрической идентичностью.
Мы делим это уравнение на квадрат косинуса и синуса.
Синус и косинус являются непрерывными функциями. У тангентов и секантов есть точки перелома: катангенез и косекансы.
Где f — произвольная тригонометрическая функция, g — соответствующая ей кофункция (т.е. косинус для синуса, синус для косинуса и подобная для других функций), n — целое число. Полученной функции предшествует знак, который имеет начальную функцию в данной координатной четверти, при условии, что угол b острый.
Формулы для работы с касательными и катангами трех углов получены путем деления правой и левой частей соответствующих уравнений, представленных выше.
Вид одного параметра.
Все тригонометрические функции могут быть выражены полукруглым касательным.
Производные и интегралы
Все тригонометрические функции непрерывно и бесконечно дифференцируются по всему диапазону определения:
Интегралы тригонометрических функций в домене выражаются элементарными функциями следующим образом.
Большинство из вышеперечисленных свойств тригонометрических функций были сохранены даже в сложном случае.
Некоторые дополнительные свойства: тригонометрическое уравнение идентичности:
Заключение
В данной работе были выполнены все задачи: получены более подробные сведения о тригонометрических функциях, приведены доказательства теорем косинуса и синуса, а также теоремы о площади треугольников, применены при решении задач по нахождению неизвестных элементов треугольника, научились применять эти теоремы при измерении работы на местности. Представленные проблемы представляют большой практический интерес, закрепляют полученные знания в области геометрии и могут быть использованы в практической работе.
Список литературы
![Помощь студентам в учёбе]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
![lfirmal]()
Образовательный сайт для студентов и школьников
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
I РАЗДЕЛ (теоретический) …………………………………….……..…4-9 стр.
II РАЗДЕЛ (практический) ………………………………………….….10-12стр.
Тема проекта и ее актуальность:
данная тема непосредственно связана с изучением технологии построения и редактирования различных видов графиков тригонометрических функций, с использованием полученных в процессе работы над проектом знаний для более глубокого изучения свойств тригонометрических функций, а также со сдачей ЕГЭ. Рассматриваемая тема имеет теоретическую и практическую значимость. Она находит широкое применение в разных разделах математики и других областях науки, и тесно связана с практической деятельностью человека.
Цель проекта:
Ø Научиться строить графики тригонометрических функций.
Ø Установить закономерности построения графиков тригонометрических функций в зависимости от коэффициентов, изменения значения аргумента и значения функции .
Ø Узнать о практическом применении тригонометрических функций в жизни человека.
1. Изучить историю возникновения тригонометрии.
2. Повторить: определение графика функции, области определения и области значения функции; определения синуса, косинуса, тангенса и котангенса в прямоугольном треугольнике; повторить табличные значения синусов, косинусов, тангенсов и котангенсов.
3. Изучить теорию: познакомиться с новым понятием - радианная мера угла, с формулами перевода градусной меры угла в радианную и обратно, вывести и выучить новые табличные значения синусов, косинусов, тангенсов, котангенсов, арксинусов, арккосинусов, арктангенсов и арккотангенсов.
4. Научиться строить графики различных тригонометрических функций.
5. Рассмотреть методы построения графиков сложных тригонометрических функций.
6. Рассмотреть задания с применением графиков тригонометрических функций на ЕГЭ.
7. Найти подтверждение применения графиков тригонометрических функций в окружающем нас мире и различных отраслях практической деятельности человека.
РАЗДЕЛ I .
Тригонометрия или тригонометрические функции используются в астрономии, в морской и воздушной навигации, в машиностроении, в теории музыки, в акустике, в оптике, в архитектуре, в метеорологии, в сейсмологии, в океанографии, в медицинской визуализации (компьютерная томография, ультразвук) , в анализе финансовых рынков, в электронике, в компьютерной графике, в разработке компьютерных игр, а также во многих науках: в теории вероятностей, в статистике, в биологии, в химии, в теории чисел, в физике и т.д. Синус и косинус имеют фундаментальное значение для теории периодических функций, например, при описании звуковых и световых волн.
Определение синуса и косинуса:
ü секансом α называется отношение гипотенузы к прилежащему катету;
ü косекансом α называется отношение гипотенузы к противолежащему катету.
Из истории возникновения тригонометрии.
К тригонометрическим функциям традиционно относят:
прямые тригонометрические функции: синус ( sin x ) и косинус ( cos x );
производные тригонометрические функции: тангенс ( \,x> tg x ) и котангенс ( \,x> ctg x );
другие тригонометрические функции: секанс ( sec x ) и косеканс \,x> (с osec x )
обратные тригонометрические функции: арксинус ( arcsin х), арккосинус ( arccos х), арктангенс ( arctg х), арккотангенс ( arcctg х).
Что касается свойств тригонометрических функций, то особое внимание нужно обратить на:
ü область определения и область значений функций, т.к. для синуса и косинуса есть ограничения в области значений, а для тангенса и котангенса ограничения в области определения;
![]()
ü периодичность всех тригонометрических функций, значения которых не изменяются при добавлении к значениям их аргумента некоторого числа T (отличного от нуля). Такой аргумент называют периодом функции и обозначают буквой T . Для синуса и косинуса T = 2 , а тангенса и котангенса.
Тригонометрические функции числового аргумента.
Функция y = sin х.
Если каждому действительному числу х поставлено в соответствие число у, равное синусу угла в х радиан, то говорят, что этим определена функция y = sin х, называемая синусом числового аргумента х.
Свойства функции y = sin х:
1. Функция y=sinх нечетная, так как sin(−х) = − sin х.
sin ( х +2 π )= sin х .
y > 0 при (0+2π k ; π+2π k ), k ∈ Z и y k ; 2π+2π k ), k ∈ Z .
График функции y = sinх - синусоида:
![]()
Функция y = cos х.
Если каждому действительному числу х поставлено в соответствие число у, равное косинусу угла в х радиан, то говорят, что этим определена функция y = cos х называемая косинусом числового аргумента х.
Свойства функции y = cos х:
![]()
y > 0 при (− +2π k ; +2π k ), k ∈ Z и y при ( +2π k ; +2π k ), k ∈ Z .
График функции y = cos α - косинусоида:
![]()
Функция y = tg х.
![]()
Если каждому действительному числу х, отличному от х= +π k , где k -любое целое число, поставлено в соответствие число у, равное тангенсу угла в х радиан, то говорят, что этим определена функция y = tg х, называемая тангенсом числового аргумента х.
![]()
D(y)=R, исключая числа х= + π k , где k ∈ Z; E(y) = (- ∞ ; + ∞).
Свойства функции y = tg х:
y > 0 при (π k ; +π k ), k ∈ Z и y +π k ; π k ), k ∈ Z.
График функции y= tgх - тангенсоида:
![]()
Функция y = сtg х.
Если каждому действительному числу х, отличному от х=π k , где k ∈ Z, поставлено в соответствие число у, равное котангенсу угла в х радиан, то говорят, что этим определена функция y = сtg х, называемая котангенсом числового аргумента х.
D(y)=R, исключая числа х= π k , где k ∈ Z; E(y) = (- ∞ ; + ∞).
Свойства функции y = сtg х:
![]()
y > 0 при (π k ; + π k ), k ∈ Z и y +π k ; π+π k ), k ∈ Z.
График функции y= сtgх - котангенсоида:
![]()
РАЗДЕЛ II
Рассмотрим построение графика тригонометрической функции на примере построения синусоиды:
Аналогично построению любого графика функции в системе координат, график синусоиды строится по точкам, полученным путем подстановки значений х в формулу y= sinх. Алгоритм построения графика синусоиды:
1. Строим особую систему координат.
2. Выбираем масштаб по оси Ох, который равен 2π , что приближенно равно 12 клеточкам, а по оси Оу 2 клеточки=1единичный отрезок.
4. Так как функция y= sinх периодическая и Т=2π , то через интервал 2π значения функции повторяются и можно продолжать волну синусоиды до бесконечности.
5. Если нужно построить более точный график, то можно взять больше точек, например , ; ; и т.д.
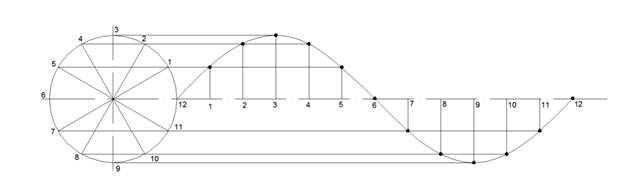
В интернете я увидела еще один метод построения синусоиды. Опишу построение, как алгоритм:
ü Окружность разделим на 12 частей.
ü Пронумеруем точки указанным способом, т.е. 1 соответствует ; 2 соответствует ; 3 соответствует и т.д.
ü Измерим длину дуги на окружности. Отложим на прямой между точками 1 и 2 соответствующее расстояние. Затем отметим точку на пересечении соответствующих чисел, т.е. точка находится под таким же номером, как и на окружности.
ü Все полученные точки последовательно соединяем плавной сплошной линией.
ü Получим искомую синусоиду.
![]()
ОБЩИЙ ВИД ПРЕОБРАЗОВАНИЯ ФУНКЦИИ (Прил.№2)
I ) Параллельный перенос графика вдоль оси абсцисс на | a | единиц:
![]()
![]()
![]()
![]()
![]()
![]()
II ) Параллельный перенос графика вдоль оси ординат на | n | единиц:
![]()
![]()
![]()
III ) Симметричное отражение графика относительно оси абсцисс:
IV ) Симметричное отражение графика относительно оси ординат:
V ) Сжатие и растяжение графика : y = kf ( x )
а) при k ˃ 1 – растяжение графика от оси абсцисс в k раз ,
б) при 0 k – сжатие графика к оси абсцисс в k раз .
VI ) Сжатие и растяжение графика: y = f ( kx ):
а) при k ˃ 1 – сжатие графика к оси ординат в k раз,
б) при 0 k – растяжение графика от оси ординат в k раз,
VII ) Преобразования графика с модулем: у = | f ( x )|:
а) При f ( x ) ˃ 0 – график остаётся без изменений,
2. Наверняка, многие видели изображение траектории полёта какого-либо космического корабля по телевидению или хотя бы на карте, например МКС. Оно напоминает синусоиду (косинусоиду). Но почему? Ведь, казалось бы, что корабль летит прямо. Попробуем разобраться. Действительно, МКС вращается по круговой орбите. Ось вращения Земли имеет наклон, примерно 24 градуса. Именно благодаря этому наклону, меняются времена года. МКС запускают так, чтобы получать максимум солнечной энергии. А эта орбита не совпадает с экватором. Таким образом, орбита МКС проходит частично по южному, а частично по северному полушарию. В сутки международная станция делает 16 оборотов вокруг Земли, поэтому южное полушарие меняется на серверное и наоборот. Отсюда и получается траектория, напоминающая синусоиду.(Прил.4).
В данном проекте, опираясь на научные источники, рассмотрен вопрос о зарождении и развитии тригонометрии как о самостоятельном разделе математики, даны определения тригонометрических функций, а также представлены способы построения графиков различных тригонометрических функций, в которых используются данные методы.
Работа над проектом способствовала развитию моих познавательных навыков, расширила умение строить графики тригонометрических функций и наблюдать за их преобразованием в зависимости от линейных преобразований самой функции. Также укрепило мое мнение о математике как универсальном языке науки. В проекте рассматривалось построение различных графиков средствами элементарной математики, что станет хорошей подготовкой к дальнейшему усвоению методов построения других тригонометрических функций, которые мы будем изучать в 11 классе. Таким образом, цель моей работы: представить способы построения графиков тригонометрических функций, рассмотреть вопросы о практическом применении тригонометрических функций в жизни человека , выполнена. Построение графиков имеет важное значение в тригонометрии, а так же важное самостоятельное прикладное значение в изучении математики.
1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 10 класс: учеб для общеобразоват. организаций: базовый и углубленный уровни/ [С.М.Никольский, М.К. Потапов, Н.Н.Решетников и др.]- М.: Просвещение, 2017.
2. h ttps :// krasavtsev . blogspot . com /2018/10/3 algebray 30. html
![https://ds05.infourok.ru/uploads/ex/0eae/0000d1fd-747b0e57/img12.jpg]()
Абуль-Вафа Мухаммад ибн Мухаммад аль-Бузджани ( Бузган , 10 июня 940 - Багдад , 998 ) - персидский учёный X века, один из крупнейших математиков и астрономов средневекового Востока.
![https://upload.wikimedia.org/wikipedia/commons/1/19/Jakob_Bernoulli.jpg]()
Я́коб Берну́лли (1655 - 1705) - швейцарский математик. Один из основателей теории вероятностей и математического анализа.
![https://pbs.twimg.com/media/EJkeKxAWsAAI9ve.jpg]()
Георг Симон Клюгель (1739-1812) - немецкий математик и физик.
![https://tochka-py.ru/mustknow/img/30393-leonard-ejler.jpg]()
Леона́рд Э́йлер (1707- 1783) - швейцарский математик и механик.
![]()
![]()
![]()
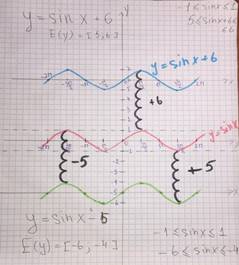
Построим график функции y = sinx и параллельно перенесём его вниз на 5 единиц вдоль Оу (так как –5 y = sinx -5.
Аналогично рассуждаем, выполняя построение графика функции y = sinx +6. Строим график функции y = sinx и параллельно перенесём его вверх на 6 единиц вдоль Оу (т. к. как 6 > 0), получим график функции y = sinx -5.
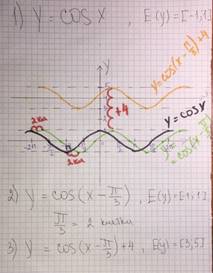
Построим график функции y = cosx и параллельно перенесем его вправо на единиц вдоль Ох (так как - ). получим график функции y = cos ( x - ).
![]()
Затем, параллельно перенесем график функции вверх на 4 единицы вдоль Оу и получим график функции y = cos ( x - )+4.
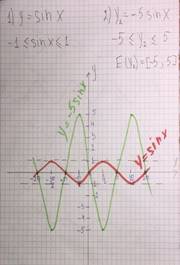
Построим график функции y = sinx . Выполним сжатие графика функции в пять раз до O у и получим график функции y =5 sinx . Затем отобразим его симметрично относительно O х и получим график функции y = - 5 sinx .
![]()
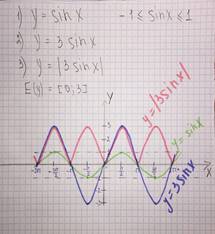
Построим график функции y = sinx . Выполним сжатие графика функции в три раза до O у . Отобразим симметрично относительно O х ту часть графика, которая находится под осью, и получим график функции y = |3 sinx |.
![]()
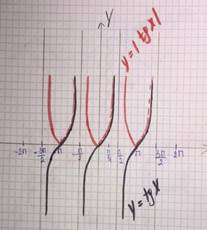
Построим график функции y = tgx . Отобразим симметрично относительно O х ту часть графика, которая находится под осью, и получим график функции y = | t gx |.
Читайте также:
1.5 Основные тригонометрические тождества…………………………….……13