Угол между векторами реферат

Обновлено: 05.07.2024

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Угол между векторами

Ранее мы с вами рассматривали угол между двумя векторами на плоскости.

Если от точки О отложить векторы ОА и ОВ, равные векторам и , соответственно, тогда угол АОВ будет являться углом между векторами и .

Обозначают угол между векторами таким образом: . То есть знак угла будем ставят над векторами.

Примеры:

Два вектора пространства могут лежать на пересекающихся и параллельных прямых, а могут лежать на скрещивающихся прямых .

Первой рассмотрим пару сонаправленных векторов.

Видим, что угол между ними равен нулю.

Также угол между векторами равен нулю, если один из них является нулевым или оба вектора нулевые.

Ведь нулевой вектор сонаправлен любому, а значит, эти случаи можно отнести к первому, где рассматривались сонаправленные векторы.

Теперь рассмотрим пару противоположно направленных векторов, отложенных от одной точки.

Видим, что угол между ними равен ста восьмидесяти градусам.

Ещё одним частным случаем являются векторы, угол между которыми равен 90 о . Такие векторы называют перпендикулярными .

Повторив всё об углах между векторами, можем приступить к решению задач по этой теме.

Задание: рассмотрим куб АBCDА ₁ B ₁ C ₁ D ₁ . Найдём углы между данными векторами.

Решение:

Задание: известно, что величина угла между векторами АB и CD равна . Найдите величины углов между векторами ВА и DC, BА и CD, АB и DC.

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно - 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = - 9 3 · 6 = - 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( - 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = - 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , - 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( - 1 ) · 3 2 2 + 0 2 + ( - 1 ) 2 · 1 2 + 2 2 + 3 2 = - 1 70 ⇒ a → , b → ^ = a r c cos ( - 1 70 ) = - a r c cos 1 70

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( - 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( - 1 ) · 3 = - 1 cos a → , b → ^ = a → , b → ^ a → · b → = - 1 5 · 14 = - 1 70 ⇒ a → , b → ^ = - a r c cos 1 70

Ответ: a → , b → ^ = - a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , - 1 ) , B ( 3 , 2 ) , C ( 7 , - 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 - 2 , - 2 - ( - 1 ) ) = ( 5 , - 1 ) B C → = ( 7 - 3 , - 2 - 2 ) = ( 4 , - 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( - 1 ) · ( - 4 ) 5 2 + ( - 1 ) 2 · 4 2 + ( - 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 - 2 · O A · O B · cos ( ∠ A O B ) ,

b → - a → 2 = a → + b → - 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 - b → - a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

ГОСТ

Угол между векторами

Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.

Пусть нам даны два вектора $\overline$ и $\overline$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $\overline=\overline$ и $\overline=\overline$, тогда угол $AOB$ будет носить название угол между двумя векторами. (рис. 1).

Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ

Причем мы будем считать, что если векторы $\overline$ и $\overline$ будут сонаправленными, или один или оба из них будет нулевым вектором, то угол между этими векторами будет равняться $0^\circ$.

Нахождение угла между векторами в пространстве с помощью скалярного произведения

Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.

Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.

Скалярное произведение двух данных векторов $\overline$ и $\overline$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, равняется сумме произведений их соответствующих координат.

Математически выглядит следующим образом

$\overline\cdot \overline=δ_1 δ_2+β_1 β_2+γ_1 γ_2$

Готовые работы на аналогичную тему

Обозначение: $\overline\cdot \overline$.

С помощью скалярного произведения мы можем найти косинус угла между векторами. Пусть нам даны векторы $\overline$ и $\overline$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, соответственно. Из определения 2 получим, что

Из теоремы 1 мы знаем, что $\overline\cdot \overline=δ_1 δ_2+β_1 β_2+γ_1 γ_2$, следовательно

Расписывая по формуле длины вектора значения $|\overline|$ и $|\overline|$, окончательно получим

Найдя значение косинуса, мы легко найдем и значение самого угла.

Найти косинус угла между векторами $\overline$ и $\overline$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.

Решение.

Найдем скалярное произведение между данными векторами через координаты:

$\overline\cdot \overline=1\cdot 3+(-2)\cdot 0+2\cdot 4=11$

Найдем длины этих векторов:

В результате, получим

Нахождение угла между векторами с помощью векторного произведения

Вспомним сначала, определение векторного произведения и каким образом его можно находить.

Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.

Математически это выглядит следующим образом:

$|\overlineх\overline|=|\overline||\overline|sin⁡∠(\overline,\overline)$
$\overlineх\overline⊥\overline$, $\overlineх\overline⊥\overline$
$(\overlineх\overline,\overline,\overline)$ и $(\overline,\overline,\overline)$ одинаково ориентированы (рис. 2)

Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ

Для нахождения вектора векторного произведения можно пользоваться следующей формулой:

$\overlineх\overline=\begin\overline&\overline&\overline\\δ_1&δ_2&δ_3\\β_1&β_2&β_3\end$

С помощью векторного произведения мы можем найти синус угла между данными векторами. Пусть нам даны векторы $\overline$ и $\overline$ с координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$, соответственно. Из определения 3 получим, что

Найдем вектор векторного произведения по формуле:

$\overlineх\overline=\begin\overline&\overline&\overline\\δ_1&δ_2&δ_3\\β_1&β_2&β_3\end=(δ_2 β_3-δ_3 β_2,δ_3 β_1-δ_1 β_3,δ_1 β_2-δ_2 β_1)$

Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.

Найти синус угла между векторами $\overline$ и $\overline$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.

Решение.

Найдем вектор векторного произведения между данными векторами по формуле:

$\overlineх\overline=\begin\overline&\overline&\overline\\1&-2&2\\3&0&4\end=-8\overline+2\overline+6\overline=(-8,1,6)$

Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.

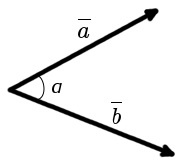
На изображении это α, который также можно обозначить следующим образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как и любой другой угол, векторный может быть представлен в нескольких вариациях.

Острый:

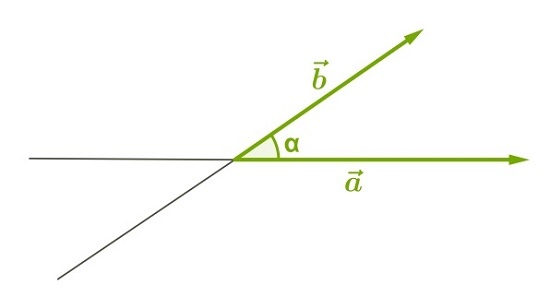
Тупой:

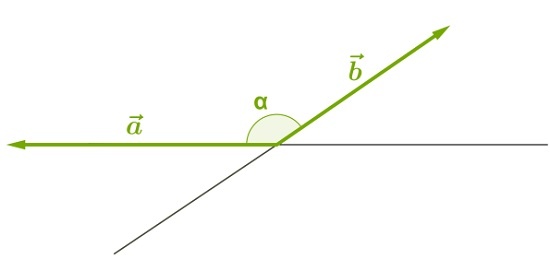
Прямой:

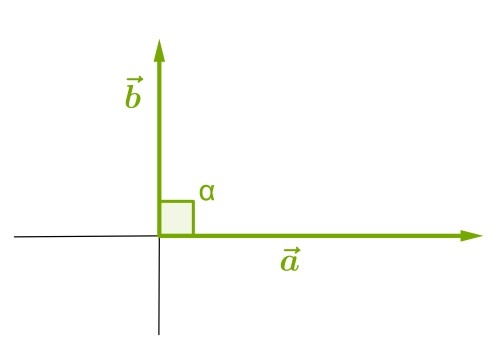
С величиной $0^\circ$ (то есть, векторы сонаправлены):

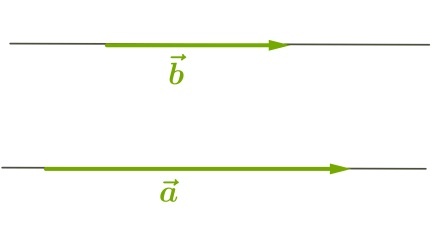
С величиной $180^\circ$ (векторы направлены в противоположные стороны):

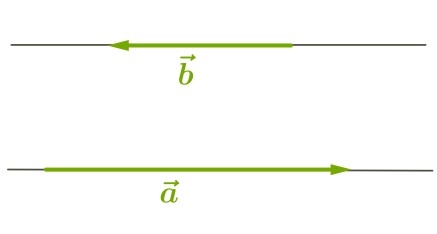
Нахождение угла между векторами

Как правило, угол между $ \overrightarrow a$ и $\overrightarrow b$ можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.

Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.

Формула скалярного произведения:

$\left(\overrightarrow a;\overrightarrow b\right)=\left|\overrightarrow a\right|\times\left|\overrightarrow b\right|\times\cos\left(\widehat<\overrightarrow a;\overrightarrow b>\right)$

Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
Если векторы имеют общую направленность, то есть угол между ними равен $0^\circ$ , а косинус — 1, то СП будет тоже положительным.
Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
Если α равен $180^\circ$ , то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
Если α — прямой, то СП равно 0, так как косинус $90^\circ$ равен 0.

В случае, если \overrightarrow a и \overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:

Расчет угла, если вектор задан координатами

В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде $\overrightarrow a=\left(a_x;a_y\right)$ и $\overrightarrow b=\left(b_x;b_y\right)$ , то угол между ними можно найти следующим образом:

Если же координаты находятся в трехмерном пространстве и заданы в виде:

то формула принимает такой вид:

Расчет угла, если заданы три точки в прямоугольной системе координат

В этом случае проще будет разобраться с объяснениями сразу на примере.

Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между $\overrightarrow$ и $\overrightarrow$ .

Решение

Для начала найдем их координаты по известным координатам заданных точек:

После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:

Примеры решения задач

Для наглядности, взглянем на примеры решения задач по данной теме.

Задача 1

Известно, что $\overrightarrow a$ и $\overrightarrow b$ . Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.

Решение

Подставим известные значения:

Далее найдем угол между данными векторами:

Задача 2

В пространстве даны координаты $\overrightarrow a=(8; -11; 7)$ и $\overrightarrow b=(-2; -7; 8)$ . Вычислить угол α между ними.

Решение

Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:

Подставляем значения и получаем:

Теперь находим угол α:

Задача 3

Известны $\overrightarrow a=(3; 4)$ и $\overrightarrow b=(2; 5)$ . Найти угол между ними.

Читайте также: