Тригонометрия на ладони реферат

Обновлено: 05.07.2024

Собрала для вас похожие темы рефератов, посмотрите, почитайте:

Введение

Я заинтересовался этой темой, потому что хотел узнать больше о тригонометрии и особенно о ее истории.

Я поставил перед собой цель: определить на основе отобранного материала, где тригонометрия, за исключением школьного курса, встречается в решении проблем и идентичностей.

Прочитав литературу, я узнал, что тригонометрические вычисления используются практически во всех областях геометрии, физики и технологии. Большое значение имеет метод триангуляции, который может быть использован для измерения расстояний до далеких звезд в астрономии, между географическими достопримечательностями для управления спутниковыми навигационными системами.

Также стоит отметить применение тригонометрии в таких областях, как теория музыки, акустика, оптика, анализ финансового рынка, электроника, теория вероятности, статистика, биология, медицина (в том числе ультразвук и компьютерная томография), фармация, химия, теория чисел (и), как следствие криптографии), сейсмологии, метеорологии, океанографии, картографии, многих областях физики, топографии и геодезии, архитектуры, фонетики, экономики, электротехники, машиностроения, компьютерной графики, кристаллографии, а также я узнал много нового, чего раньше не знал.

По истории тригонометрии

Тригонометрия — греческое слово и буквально означает измерение треугольников (Триггунон — треугольник и измерение Метрю).

В этом случае под измерением треугольников следует понимать треугольное решение, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, но также и задачи планаметрии, стереометрии, астрономии и другие даны задачам решения треугольников.

Появление тригонометрии связано с астрономией и строительством.

Хотя название науки появилось сравнительно недавно, многие понятия и факты, связанные с тригонометрией, были известны уже две тысячи лет назад.

Решения для треугольников, основанные на зависимостях между сторонами и углами треугольника, были впервые найдены древнегреческими астрономами Гиппархом (II в. до н.э.) и Клавдием Птолемеем (II в. н.э.). Позже отношения между сторонами треугольника и его углами стали называться тригонометрическими функциями.

В долгой истории существует понятие синуса. Фактически, различные соотношения сечений треугольника и круга (а по существу, и тригонометрические функции) встречаются уже в III в. до н.э. в трудах великих математиков Древней Греции — Евклида, Архимеда, Аполлонии Пергусской. В римский период эти отношения систематически изучались Менелаем (I в. н.э.), хотя конкретное название им не давалось. Современный синус a, например, изучался как полуаккорд, на котором центральный угол лежит в размере a, или как двухдуговой аккорд.

Уже в IV-V веке в астрономических трудах великого индийского ученого Ариабхаты, чье имя было дано первому индийскому спутнику Земли, существовал особый термин. Он назвал отрезок АМ (рис. 1) аргаджива (арга — половина, джива — луковая струна, которая напоминает аккорд). Позже появилось более короткое имя Джива. Арабские математики в IX в. заменили это слово на арабское слово jib (выпуклость). В переводе арабских математических текстов в этом столетии он был заменен на латинский синус (синус — кривизна, изгиб).

Касательные появились в связи с решением задачи определения длины тени. Тангент (как и кокангент) был введен в X. столетие арабский математик Абу-л-Вафа, который создал первые таблицы для нахождения тангенса и кокангента. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенты были заново открыты только в XIV веке немецким математиком и астрономом Реджимонтаном (1467 г.). Он доказал теорему о тангенте. Regimontan также сделал подробные тригонометрические таблицы, благодаря его работам плоские и сферические тригонометрии стали отдельной дисциплиной в Европе.

Дальнейшее развитие тригонометрии состоялось в трудах выдающегося астронома Николая Коперника (1473-1543) — создателя мировой гелиоцентрической системы Тихо Браге (1546-1601) и Иоганна Кеплера (1571-1630), а также в трудах математика Франсуа Виета (1540-1603), который полностью решил задачу определения всех элементов плоского или сферического треугольника на три даты.

Долгое время тригонометрия была чисто геометрической. Факты, которые мы сейчас формулируем в виде тригонометрических функций, были сформулированы и доказаны с помощью геометрических концепций и высказываний. Так было уже в средние века, хотя иногда использовались аналитические методы, особенно после появления логарифмов. Пожалуй, наибольший стимул для развития тригонометрии возник в связи с решением астрономических задач, представлявших большой практический интерес (например, для решения задач определения положения корабля, прогнозирования отключения электроэнергии и т.д.). Астрономов интересовали отношения между сторонами и углами сферических треугольников. И надо сказать, что математики древнего мира успешно справились с поставленными задачами.

С XVII века тригонометрические функции стали использоваться для решения уравнений, задач механики, оптики, электротехники, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, изучения переменного тока и др. Поэтому тригонометрические функции были всесторонне и глубоко исследованы и приобрели значение для всей математики.

Аналитическая теория тригонометрических функций была разработана в основном Леонардом Эйлером (1707-1783), выдающимся математиком XVIII века, членом Санкт-Петербургской Академии наук. Большое научное наследие Эйлера включает в себя блестящие результаты, связанные с математическим анализом, геометрией, теорией чисел, механикой и другими математическими приложениями. Именно Эйлер первым ввел известные определения тригонометрических функций, начал рассматривать функции любого угла, и получил формулы редукции. По словам Эйлера, тригонометрия получила форму расчета: различные факты стали доказываться формальным применением формул тригонометрии, доказательства стали намного компактнее.

Таким образом, тригонометрия, зародившаяся как наука о разрешении треугольников, со временем переросла в науку о тригонометрических функциях.

Тригонометрические функции

Элементарные функции, которые исторически возникали при взгляде на прямоугольные треугольники и выражают зависимость сторон этих треугольников от острых углов гипотенузы (или, эквивалентно, зависимость аккордов и высоты от центрального угла в круге). Эти функции нашли самое широкое применение в различных областях науки. В результате было расширено определение тригонометрических функций, и их аргументом теперь может быть любое реальное или даже сложное число.

Наука, изучающая свойства тригонометрических функций, называется тригонометрией.

Ссылка на тригонометрические функции:

Во-первых, прямые тригонометрические функции:

Во-вторых, противоположные тригонометрические функции:

В-третьих, производные тригонометрические функции:

В западной литературе загар х, кроватка х, цхх называются загаром, кроватка х, цхх.

В дополнение к этим шести, существуют также некоторые редко используемые тригонометрические функции (верна и т.д.) и обратные тригонометрические функции (арксин, аркозин и т.д.), которые рассматриваются в отдельных статьях.

Синусоидальный и косинусоидальный вещественные аргументы являются периодически непрерывными и бесконечно дифференцируемыми вещественными функциями.

Остальные четыре функции на реальной оси также являются материально значимыми, периодическими и бесконечно различимыми в областях определения, но не непрерывными.

Тангенты и секанты имеют паузы второго поколения на ±rp, в то время как катангенсы и секанты имеют паузы на ±rp.

Геометрическое определение

Обычно тригонометрические функции определяются геометрически. Укажем декартовую систему координат на плоскости и сформируем окружность радиусом R, центр которой находится в начале координат O. Измеряем углы как вращения от положительного направления оси абсциссы к акустическому пучку. Направление против часовой стрелки считается положительным, направление по часовой — отрицательным. Если мы обозначим абсциссой точку B с xB, то мы обозначим ординату с yB.

Понятно, что значения тригонометрических функций не зависят от радиуса окружности R из-за свойств подобных фигур.

Следует также отметить, что этот радиус часто принимается равным значению одного сечения.

Исходя из этого, синус является просто ординатой yB, а косинус — абсциссой xB.

Если b является вещественным числом, то в математическом анализе синус b называется угловым синусом, радиан которого равен b, аналогично другим тригонометрическим функциям.

Рассмотрим графическое изображение этого явления на рисунке 3.

Определение тригонометрических функций как решений дифференциальных уравнений, уравнений функций и по ряду

Во многих учебниках элементарной геометрии тригонометрические функции острого угла до сих пор определялись как отношения сторон прямоугольного треугольника. Пусть ОАБ будет треугольником с углом b.

Ну, тогда:

Синус угла b называется отношением AB/OB (отношение противоположного катетера к гипотенузе);
Козин угла b называется отношением OA/OB (отношение смежного катетера к гипотенузе);
Касательная угла b называется отношением AB/OA (отношение противоположного катетера к соседнему катетеру);
Катангензис угла b называется отношением OA/AB (отношение смежного катетера к противоположному катетеру);
Секанс угла b называется отношением ОВ/ОА (отношение гипотенузы к соседнему катетеру);
Угол cosecansome b называется отношением OV/AB (отношение гипотенузы к контркатетеру).

После того, как мы построили систему координат с началом в точке О, изменили направление оси абсциссы вдоль ОА и, при необходимости, ориентацию треугольника (перевернув его) так, чтобы он лежал в первой четверти системы координат, а затем построили окружность с радиусом, равным гипотенусе, сразу замечаем, что такое определение функций приводит к тому же результату, что и предыдущее.

На основании геометрии и свойств предельных значений можно доказать, что производная синуса равна косинусу, а производная косинуса равна минус синус. Затем можно использовать преимущества теории рядов Тейлора и представить синус и косинус как сумму степенных рядов.

Самые простые личности

Тригонометрические тождества — это математические выражения для тригонометрических функций, которые выполняются по всем значениям аргумента (из общего диапазона определений).

Поскольку синус и косинус являются ординатой и абсциссой точки, соответствующей единичной окружности впадин, то в соответствии с уравнением единичной окружности или пифагорейской теоремой.

Это соотношение называется базовой тригонометрической идентичностью.

Мы делим это уравнение на квадрат косинуса и синуса.

Синус и косинус являются непрерывными функциями. У тангентов и секантов есть точки перелома: катангенез и косекансы.

Где f — произвольная тригонометрическая функция, g — соответствующая ей кофункция (т.е. косинус для синуса, синус для косинуса и подобная для других функций), n — целое число. Полученной функции предшествует знак, который имеет начальную функцию в данной координатной четверти, при условии, что угол b острый.

Формулы для работы с касательными и катангами трех углов получены путем деления правой и левой частей соответствующих уравнений, представленных выше.

Вид одного параметра.

Все тригонометрические функции могут быть выражены полукруглым касательным.

Производные и интегралы

Все тригонометрические функции непрерывно и бесконечно дифференцируются по всему диапазону определения:

Интегралы тригонометрических функций в домене выражаются элементарными функциями следующим образом.

Большинство из вышеперечисленных свойств тригонометрических функций были сохранены даже в сложном случае.

Некоторые дополнительные свойства: тригонометрическое уравнение идентичности:

Сложные синусоидальные и косинусоидальные значения, в отличие от реальных, могут принимать любое количество значений модуля;
Все нули сложного синуса и косинуса лежат на оси материала.

Заключение

В данной работе были выполнены все задачи: получены более подробные сведения о тригонометрических функциях, приведены доказательства теорем косинуса и синуса, а также теоремы о площади треугольников, применены при решении задач по нахождению неизвестных элементов треугольника, научились применять эти теоремы при измерении работы на местности. Представленные проблемы представляют большой практический интерес, закрепляют полученные знания в области геометрии и могут быть использованы в практической работе.

Список литературы

Образовательный сайт для студентов и школьников

Синус угла - отношение противолежащей (углу) стороны к гипотенузе. Косинус - отношение прилежащей к гипотенузе. Тангенс - противолежащей стороны в прилежащей стороне Котангенс - прилежащей к противолежащей.

Для многих ребят в школе тригонометрия – один из самых трудных, непонятных разделов математики. С первых уроков уже идёт отторжение и нежелание изучать её, вникать в глубины, запоминать правила, значения функций.

Для облегчения запоминания, что косинус угла – это абсцисса точки, а синус угла – это ордината точки единичной окружности используем закон соответствия. Предлагаю ребятам посмотреть на начальные буквы функций (косинус, синус), начальные буквы координат (абсцисса, ордината) и записать их в алфавитном порядке: в первой строке – функции, во второй – координаты.

А значения синуса и косинуса для углов 0°, 30°, 45°, 60°, 90° легко вычислить с помощью левой руки. Для этого:

Пронумеруем пальцы от большого до мизинца, счет начинаем с нуля (рис. 1).

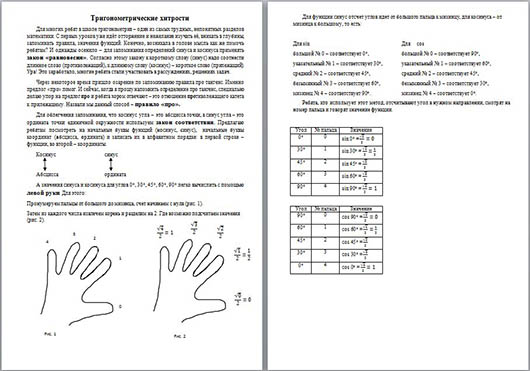
Затем из каждого числа извлечем корень и разделим на 2. Где возможно подсчитаем значения (рис. 2).

Для функции синус отсчет углов идет от большого пальца к мизинцу, для косинуса – от мизинца к большому, то есть:

Для sin Для cos

большой № 0 – соответствует 0°, большой № 0 – соответствует 90°,

указательный № 1 – соответствует 30°, указательный № 1 – соответствует 60°,

средний № 2 – соответствует 45°, средний № 2 – соответствует 45°,

безымянный № 3 – соответствует 60°, безымянный № 3 – соответствует 30°,

мизинец № 4 – соответствует 90°. мизинец № 4 – соответствует 0°.

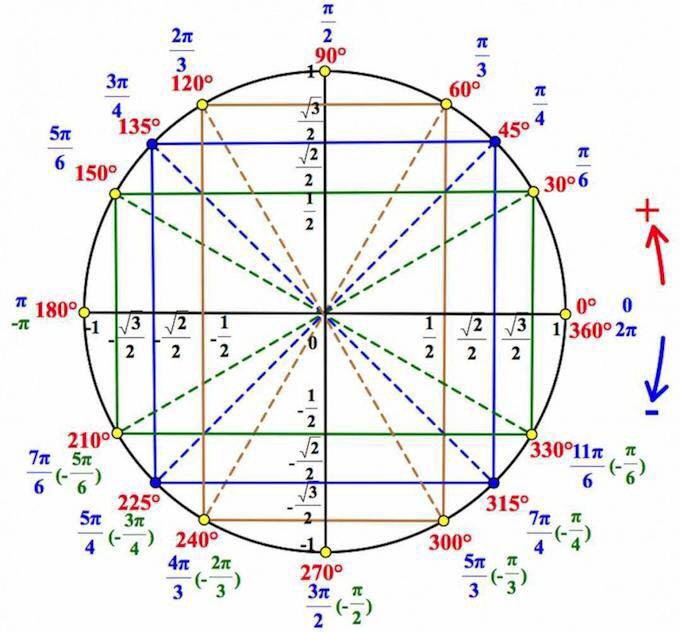
Значение котангенса - это перевернутое значение тангенса. В итоге получаем вот такую штуку: Обратите внимание, что тангенс не существует в П/2, например. Подумайте почему. (На ноль делить нельзя.) Что тут нужно запомнить: синус - это значение у, косинус - значение х. Тангенс - это отношение у к х, а котангенс - наоборот. так что, чтобы определять значения синусов/косинусов достаточно нарисовать табличку, которую я выше рассказал и круг с осями координат (по ней удобно смотреть значения при углах 0, 90, 180, 360). Я надеюсь, что вы умеете различать четверти: От того, в какой четверти находится угол, зависит знак его синуса, косинуса и тд. Хотя, абсолютно примитивные логически размышления выведут вас на верный ответ, если вы будете учитывать, что во второй и третьей четверти х отрицателен, а у отрицателен в третьей и четвертой.

Что нужно знать, уметь и делать, чтобы переводить углы в первую четверть: -разложить угол на удобоваримые слагаемые; -учесть, в какой четверти находится угол, и поставить соответствующий знак, если функция в этой четверти отрицательна или положительна; -избавиться от лишнего: *если надо избавиться от 90, 270, 450 и остальные 90+180n, где n - любое целое число, то функция меняется на противоположную (синус на косинус, тангенс на котангенс и наоборот); *если надо избавиться от 180 и остальных 180+180n, где n - любое целое число, то функция не меняется.

Ваш браузер должен поддерживать фреймы Ваш браузер должен поддерживать фреймы--> --> Ваш браузер должен поддерживать фреймы--> --> Ваш браузер должен поддерживать фреймы--> -->

-75%

Проект выполнен в форме презенации. Включает в себя разделы:

Из истории тригонометрии
О тригонометрии
Тригонометрия в ладони
Методический материал
Дидактический материал

Проект предназначен для использования учителями математики.

Урок алгебры 9 класс

Тема. «ВВЕДЕНИЕ

Из истории тригонометрии
Тригонометрия в ладони
Методический материал
Дидактический материал
Аннотация
Литература
Автор

Из истории тригонометрии

ТРЕУГОЛЬНИК

Т Р И Г О Н

М Е Т Р И О

ТРИГОН О МЕТРИЯ

Из истории тригонометрии

Потребность в измерении углов возникла так же давно, как и потребность в измерении расстояний. Одним из стимулов развития тригонометрии была необходимость определения времени, определения положения корабля в открытом море или каравана в пустыне.

Некоторыми знаниями тригонометрии владели ученые Древнего Вавилона. Об этом свидетельствует тот факт, что вавилоняне умели предсказывать солнечные и лунные затмения. На одной из глиняных табличек Древнего Вавилона (2 тыс. лет до н. э.) решается задача, в которой по известному диаметру круга и высоте сегмента вычисляется длина хорды, что соответствует установлению связи между синусом и косинусом

Из истории тригонометрии

Первая книга в Европе, в которой тригонометрия рассматривалась как самостоя-тельная дисциплина, появилась в XV в. Ее написал И. Мюллер (1436 — 1476).

Затем появились сочи-нения Н. Коперника, И. Кеп-лера

В этих работах развитие тригонометрии в основном было направлено на потребности астрономии.

Из истории тригонометрии

Особую роль в развитии тригонометрии сыграли работы Л. Эйлера, который разработал теорию тригонометрических функций.

Ещё тогда тригонометрия приобрела современный вид.

Впервые обозначать синус и косинус знаками sin x и cos x стал И. Бернулли в письме 1739 г. к Эйлеру. Эйлер принял эти обозначения и систе-матически применял их.

Тригонометрия в ладони

Сейчас мы измерим углы между вашими пальцами.

Берём два прямоугольных треугольника с углами 30°и 45 ° и приложим вершину нужного угла к бугру Луны на ладони.

Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону — с одним из остальных.

Тригонометрия в ладони

Прикладываем угол в 30°; оказывается, это угол

между мизинцем и безымянным пальцем;

между мизинцем и средним пальцем — 45°,

между мизинцем и указательным пальцем — 60°,

между мизинцем и большим пальцем — 90°.

И это у всех людей без исключения

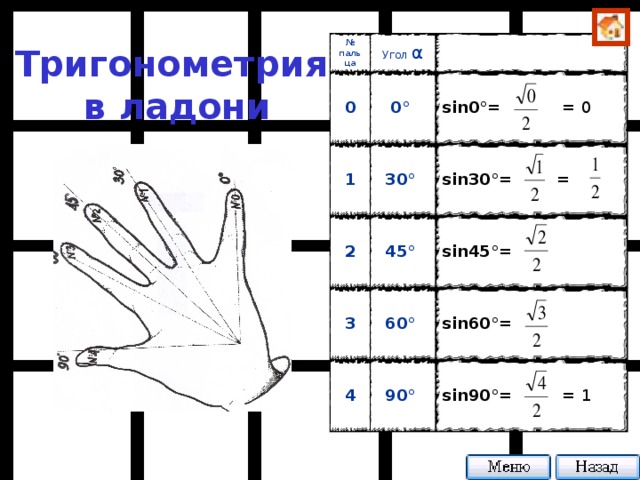
sin 0 ° = = 0

sin 30 ° = =

sin 45 ° =

sin 60 ° =

sin 90 ° = = 1

Тригонометрия в ладони

Методический материал

Протяните руку (любую) и разведите как можно сильнее пальцы, так, как показано на рисунке

Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а потому введем нумерацию пальцев.

Методический материал

мизинец № 0 — соответствует 0°

безымянный № 1 — соответствует 30°

средний № 2 — соответствует 45°

указательный № 3 — соответствует 60°

большой № 4 — соответствует 90°.

Таким образом, у всех людей на руке четыре пальца.

Методический материал

Таким образом, у всех людей на руке четыре пальца.

А теперь, ребята, запомните формулу:

SIN  =

половина квадратного корня из номера (п) пальца

Дидактический материал

Решите задания самостоятельной работы

Вариант 1 и Вариант 2

со взаимопроверкой

1. Какой знак имеет:

a) sin 169°; б ) cos 110°; в ) tg103°; г ) ctg 288°;

a) sin 409°; б ) cos 372º; в ) tg 540°; г ) ctg364°;

a) sin(-88°); б ) cos (-12°); в ) tg(-72°); г )ctg(110°)?

2. Укажите в таблице соответствующий знак синуса, косинуса, тангенса и котангенса:

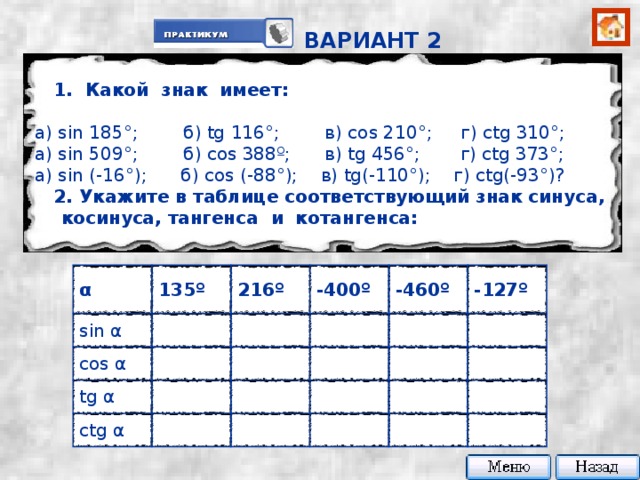
1. Какой знак имеет:

a) sin 185 °; б ) tg 116°; в ) cos 210°; г ) ctg 310°;

a) sin 509 °; б ) cos 388º; в ) tg 456°; г ) ctg 373°;

a) sin (- 16 °); б ) cos (-88°); в ) tg(-110°); г ) ctg(-93°)?

2. Укажите в таблице соответствующий знак синуса, косинуса, тангенса и котангенса:

135 º

216 º

- 400 º

- 460 º

-127 º

Выпускной проект

Проект выполнен в виде презентации. Включает в себя разделы

Из истории тригонометрии
Тригонометрия в ладони
Методический материал
Дидактический материал

Проект предназначен для использования учителями математики в практической деятельности.

Задача, поставленная при создании проекта : Овладеть технологиями создания презентации, методами и способами поиска информации в Сети.

Геометрия - одна из самых древних и интересных наук, занимающаяся изучением геометрических фигур. Наш мир невозможно представить без их существования. Эта наука имеет огромный запас различных теорем, которые постоянно применяются как при решении математических задач, так и в жизни. Больше всего меня заинтересовали теоремы синусов и косинусов, которые применяются при решении произвольных треугольников. Цель данного реферата - уметь доказывать теоремы косинусов и синусов, применять их в решении задач, выбирать правильный ход решения при их использовании, знать, где данные теоремы применяются в жизни.

Треугольники

Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки - его сторонами.

Виды треугольников :

· Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

· Треугольник, у которого все стороны равны, называется равносторонним или правильным.

· Треугольник называется прямоугольным , если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой , две другие стороны называются катетами .

· Треугольник называется остроугольным , если все три его угла – острые, то есть меньше 90°

· Треугольник называется тупоугольным, если один из его углов – тупой, то есть больше 90°.

Бермудский Треугольник - широко известная аномальная зона. Расположен он в границах между Бермудскими островами, Майями во Флориде и Пуэрто-Рико. Площадь Бермудского треугольника составляет свыше одного миллиона квадратных километров. Рельеф дна в этой акватории хорошо изучен. На шельфе, который составляет значительную часть этого дна, было проведено множество бурений с целью отыскать нефть и другие полезные ископаемые. Течение, температура воды в разное время года, ее соленость и движение воздушных масс над океаном - все эти природные данные занесены во все специальные каталоги. Этот район не особенно сильно отличается от других похожих географических мест. И, тем не менее, именно в районе Бермудского треугольника загадочно исчезали суда, а затем и самолеты.

Выдвигаются различные гипотезы для объяснения этих исчезновений, от необычных погодных явлений до похищений инопланетянами. Скептики утверждают, однако, что исчезновения судов в бермудском треугольнике происходят не чаще, чем в других районах мирового океана и объясняются естественными причинами.Морские и воздушные суда погибают и в других районах земного шара, иногда бесследно. Неисправность радио или внезапность катастрофы может помешать экипажу передать сигнал бедствия. Поиск обломков в море — непростая задача, особенно в шторм или когда место катастрофы точно неизвестно. Если учесть очень оживлённое движение в районе бермудского треугольника, частые циклоны и штормы, большое количество отмелей, количество случившихся здесь катастроф, которые так и не получили объяснения, не является необычно большим.

Египетский треугольник — прямоугольный треугольник с соотношением сторон 3:4:5.

Особенностью такого треугольника, известной ещё со времён античности, является то, что при таком отношении сторон теорема Пифагора даёт целые квадраты как катетов, так и гипотенузы, то есть 9:16:25. Египетский треугольник является простейшим (и первым известным) из Героновых треугольников — треугольников с целочисленными сторонами и площадями.

Название треугольнику с таким отношением сторон дали эллины: в VII - V веках до н. э. греческие философы и общественные деятели активно посещали Египет. Так, например, Пифагор в 535 до н. э. по настоянию Фалеса для изучения астрономии и математики отправился в Египет — и, судя по всему, именно попытка обобщения отношения квадратов, характерного для египетского треугольника, на любые прямоугольные треугольники и привела Пифагора к доказательству знаменитой теоремы.

Египетский треугольник с соотношением сторон 3:4:5 активно применялся для построения прямых углов землемерами и архитекторами.

Для построения прямого угла использовался шнур или верёвка, разделённая отметками (узлами) на 12 (3+4+5) частей: треугольник, построенный натяжением такого шнура, с весьма высокой точностью оказывался прямоугольным и сами шнуры-катеты являлись направляющими для кладки прямого угла сооружения.

В архитектуресредних веков египетский треугольник применялся для построения схем пропорциональности.

Общие сведения о тригонометрических функциях

Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников.

В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.

Возникновение тригонометрии связано с землемерением, астрономией и строительным делом. Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.

Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Длительную историю имеет понятие синус . Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус a, например, изучался как полухорда, на которую опирается центральный угол величиной a, или как хорда удвоенной дуги. В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).

Слово косинус намного моложе. Косинус – это сокращение латинского выражения completelysinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin(90° - a)). Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе.

Современные обозначения синуса и косинуса знаками sin и cos были впервые введены в 1739 г. швейцарским математиком Иоганном Бернуллив письме к Леонарду Эйлеру, который и стал употреблять их в своих математических работах. Эйлер ввел также обозначения для функций угла х: tg x , ct g x , sec x , cosec x .

· Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе (AB/OB).

· Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе (ОА/OB).

· Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету (AB/OA).

· Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету (ОА/AB) .

Значения тригонометрических функций для некоторых углов.

0°(0 рад)	30° (π/6)	45° (π/4)	60° (π/3)	90° (π/2)	180° (π)	270° (3π/2)	360° (2π)
N/A	N/A
N/A	N/A	N/A

Значения косинуса и синуса на окружности.

Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или основному тригонометрическому тождеству, имеем:

Деля это уравнение на квадрат косинуса и синуса соответственно, имеем далее:

Формулы приведения:

sin(180° - α) = sinα

cos(180° - α) = - cosα

Чётность и нечетность функций.

Чётная функция - функция y = f ( x ) называется чётной, если область её определения симметрична относительно 0 и для любого значения аргумента Х верно равенство

f (- x ) = f ( x )

Нечётная функция - функция, область её определения симметрична относительно 0 и для любого значения аргумента Х верно равенство

f(- x) = - f( x)

Косинус — единственная чётная функция. Остальные три функции — нечётные, то есть:

Теоремы

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.

S = ½ ab sin C

Дано:

∆ АВС, АВ= с, ВС = a , СА = b , h - высота

Доказать:

S = ½ absinC

Доказательство:

Введём систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Сх , а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S = ½ ah , где h – высота треугольника. Но h равна ординате точки А , т.е. h = b sinC (т.к. sinC = h / b ) => S = ½ absinC

Стороны треугольника пропорциональны синусам противолежащих углов.

a/ sinA = b/ sin B = c/ sinC

Дано:

∆АВС АВ= с, ВС= а, СА= b

Доказать :

a/ sinA = b/ sin B = c/ sinC

Доказательство:

По теореме о площади треугольника S= ½ absinC, S = ½ bcsinA, S= ½ acsinB.

Из первых двух равенств получаем ½ absinC = ½ bcsinA,

½ ab sinC = ½ bc sinA │ : ½ b

a sinC = c sinA │: sinA sinC

Точно также из второго и третьего равенства получаем

½ bc sinA = ½ ac sinB │: ½ c

b sinA = a sinB │: sinA sinB

Таккакa/sinA = c/sinC иb/sinB = a/sinA, тоa/sinA= b/sinB= c/sinC.

Замечание:

Отношение стороны треугольника к синусу противолежащего

угла равно диаметру описанной окружности.

a/sinA= b/sinB= c/sinC= 2R

Дано:

R – радиус описанной окружности, ВС = a, BA1 - диаметр

Доказать:

BC/sinA = 2R (BC=2RsinA)

Доказательство:

Проведем диаметр ВА1. Рассмотрим ∆А1ВС, ∟С - прямоугольный => ВС=ВА1×sinA1. Если т.А1 лежит на дуге ВАС, то ∟А1=∟А, если на дуге BDC, то ∟A1= 180° - ∟A. И в том, и в другом случае sinA1 = sinA => BC= BA1*sinA, BC= 2RsinAили BC/sinA= 2R.

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

a 2 = b 2 + c 2 − 2bc cosα .

Дано:
∆АВС АВ= с, ВС= а, СА= b

Доказать:

a 2 = b 2 + c 2 − 2bc cosα

Доказательство:

Введем систему координат с началом в точке А. Точка В имеет координаты (с; 0), а точка С(bcosA; bsinA). По формуле расстояния между двумя точками d2 = (x2 – x1)2 + (y2 – y1)2получаем:

ВС 2 = a 2 = (b cosA – c) 2 +(bsinА- 0) 2 ,

a 2 = b 2 cos2A - 2bc cosA + c 2 + b 2 sin 2 A,

a 2 = b 2 (cos2A + sin2A) + c 2 - 2bc cosA,

a 2 = b 2 + c 2 – 2bc cosA.

Обобщенная теорема Пифагора.

Теорему косинусов называют иногда обобщенной теоремой Пифагора. Такое название объясняется тем, что в теореме косинусов содержится как частный случай теорема Пифагора. В самом деле, если в ∆АВС ∟А прямой, то cosA = cos 90° = 0 и по a 2 = b 2 + c 2 − 2bc cosα получаем:

a 2 = b 2 + c 2 ,

т.е. квадрат гипотенузы равен сумме квадратов катета.

Задачи

Решение треугольника по двум сторонам и углу между ними.

Дано :

a = 7 см, b = 23cм, ∟ C = 130°

Найти: с , ∟ А, ∟ В

Решение :

c 2 = a 2 + b 2 − 2bc cosC

cos A = b 2 + c 2 − a 2 / 2bc

Решение треугольника по стороне и прилежащим к ней углам.

Дано:

а= 20 см, ∟ А= 75°, ∟ В= 60°

Найти: ∟ C , b , c

Решение:

a /sin A = b /sin B = c /sin C

b = a × (sin B / sin A )

c = a × (sin C / sin A )

Решение треугольника по трем сторонам.

Дано:

а= 7 см, b =2 см, с =8 см

Найти: ∟ А, ∟ В, ∟ С.

Решение:

∟ С = 180° - (54° + 13°) = 113°

№4

Измерение высоты предмета.

Предположим, что требуется определить высоту АН какого – то предмета. Для этого отметим точку В на определённом расстоянии а от основания Н предмета и измерим ∟АВН=a. По этим данным из прямоугольного треугольника АНВ находим высоту предмета: АН = а tg a.

Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии а друг от друга и измерим углы АВН и АСВ: ∟АВН =a, ∟АСВ = b, ∟ВАС = a –b.Эти данные позволяют определить все элементы треугольника АВС; по теореме синусов находим АВ: АВ = asinb/ sin (a –b). Из прямоугольного треугольника АВН находим высоту АН предмета:

АН = АВ sin a= a sina sinb / sin ( a –b).

№5

Измерение расстояния до недоступной точки (измерение ширины реки).

На местности выберем точку В и измерим длину с отрезка АВ. Затем измерим, например с помощью астролябии, углы А и В: ∟А= a и ∟В = b. Эти данные, т.е. с , a и b, позволяют решить ∆АВС и найти искомое расстояние d=AC.

Находим ∟С и sinC : ∟С= 180°- a –b, sin C= sin(180°- a –b) = sin(a+b).

Так как d/sinb = c/sinC, то d = csinb/ sin(a+b).

В данном реферате были выполнены все поставленные задачи: узнали более подробную информацию о тригонометрических функциях; привели доказательства теорем косинусов и синусов, а также теоремы о площади треугольников, применили их в решении задач на нахождение неизвестных элементов треугольника, узнали, как используются данные теоремы при проведении измерительных работ на местности. Приведенные задачи имеют значительный практический интерес, закрепляют полученные знания по геометрии и могут использоваться для практических работ.

1. Анатасян Л.С., Бутузов В.Ф. Геометрия 7-9 класс – 12-е изд.-М.: Просвещение, 2002г., стр.157-159, 256-261

3. Берманд А. Ф. Тригонометрия, 1967г., стр.4-6

4. Макарычев Ю.Н., Миндюк Н.Г. Алгебра 9 класс – 13-е изд.-М.: Просвещение, 2006г., стр.112-114

Читайте также: