Теорема способы доказательства теорем реферат

Обновлено: 05.07.2024

Содержание работы

Введение………………………………………………………………………3
Глава 1. Теоретические основы методики обучения учащихся доказательству теорем
1.1. Понятие теоремы. Строение математических теорем………………..5
1.2. Методы доказательства математических теорем
Глава 2. Методика обучения доказательству теорем…………………
Общие приемы работы с теоремами (Этапы работы с теоремами. Приемы мотивации изучения и доказательства теорем)
…………………………….
Методика организации работы с теоремами при изучении курса геометрии в 7-9 классах…….
Заключение ………………………………………….………………………40
Список использованной литературы……………………………………….42

Содержимое работы - 1 файл

Metodika_teoremy_1 (Восстановлен).doc

А это условие перпендикулярности векторов, т. е. .

Аналогично доказывается, что .[дал. с.44]

Метод доказательства, основанный на перемещении плоскости.

Пример: Доказать, что если пятиугольник имеет две оси симметрии, то он правильный.

Каждая из них проходит через вершину и середину противоположной стороны. Если одна ось проходит через вершину А₁ и середину стороны А₃А₄, то имеем А₁А₂=А₁А₅, A₂A₃ = А₅A₄, А₂ = А₅, А₃ =А₄.

Сопоставляя полученные соотношения, получаем, что пятиугольник А₁А₂A₃A₄А₅ правильный.

В данной главе мы рассмотрели теоретические основы методики обучения учащихся доказательству теорем, выяснили виды теорем, их формулировки, а также разобрали на примерах основные методы доказательства теорем. Каждый из рассмотренных методов обладает как достоинствами, так и недостатками. Поэтому ни один из них не может быть рекомендован в качестве универсального и единственного. [дан. 79] Четкое знание сущности методов явится надежным орудием в руках учащихся для самостоятельного отыскания решений задач и во многих случаях поможет учащимся найти решение задач более простое, короткое изящное.

Глава 2. Методика обучения доказательству теорем

изучения и доказательства теорем

Изучая методы работы учителей можно выяснить, чем достигается успех. Ученики формально усваивают материал обычно у тех учителей, которые излагают теоремы догматически. Учитель сообщает формулировку теоремы, сам приводит её доказательство, которое затем повторяется несколькими учениками. Если в процессе доказательства педагог задает детям вопросы, то чаще всего они касаются формулировок ранее пройденных теорем и определений, но не вскрывают путей к отысканию доказательства. Учащимся непонятно, почему появилась именно эта теорема, зачем делается то или иное дополнительное построение.

Совсем иначе идет работа у тех учителей, которые привлекают школьников к разбору содержания теоремы и к самостоятельным поискам тех логических связей, на которых построено ее доказательство. Такая творческая работа вызвает интерес учащихся и тем самым повышает активность их внимания. Результатом является не пассивное запоминание, а усвоение самого смысла доказательства.

Изучение каждой теоремы дает возможность поставить перед учениками две задачи: 1) выявить некоторые свойства изучаемого объекта и 2) логически обосновать необходимость этих свойств. [гастева,с.517]

Г.И. Саранцев [сар.,70] выделяет следующие этапы изучения теоремы:

Мотивация изучения теоремы.
Ознакомление с фактом, отраженным в теореме.
Формулировка теоремы и выяснение смысла каждого слова в формулировке теоремы.
Усвоение содержания теоремы;
Запоминание формулировки теоремы;
Ознакомление со способами ее доказательства;
Доказательство теоремы;
Применение теоремы;
Установление связей теоремы с ранее изученными теоремами.

Главным, по мнению автора, в изучении теорем является не заучивание их и их доказательств, а открытие школьниками теоремы, способа доказательства, самостоятельное конструирование доказательства, применение теоремы, применение теоремы в различных ситуациях, установление связей с другими теоремами.

С теоремой о сумме углов треугольника учащиеся могут ознакомиться, измеряя непосредственно углы треугольника. Обобщая результаты измерений, учащиеся приходят к выводу, что сумма углов треугольника равна 180 0 .

Чтобы помочь учащимся самостоятельно найти путь дедуктивного обоснования догадки, можно предложить решить задачу.

Задача. Через вершину треугольника проведена прямая, параллельная основанию. Доказать, что углы, образованные этой прямой с боковыми сторонами треугольника, соответственно равны углам треугольника при основании.

Решение этой задачи открывает путь доказательства сформулированной догадки.

Для закрепления можно предложить следующие задачи [погор, с. 63]:

Для усвоения содержания теоремы можно использовать упражнения на выделение условия и заключения теоремы; на вычленение на чертежах, моделях таких фигур, которые удовлетворяли бы условию теоремы.

Саранцев Г.И. [12] предлагает пользоваться следующей схемой (схема 1):

Этапы работы с теоремой

Упражнения, реализующие их

Установление связей теоремы с ранее изученными теоремами.

Упражнение на измерение величин, на оперирование моделями фигур

Упражнения с практическим содержанием

Упражнения на применение ранее изученных теорем и понятий

Упражнения на выделение условия и заключения теоремы

Упражнение на распознавание ситуаций, удовлетворяющих теореме

Упражнение на выполнение чертежей, моделирующих условие теоремы

Упражнение на ознакомление с методом доказательства теоремы

Упражнения, моделирующие способ доказательства теоремы

Упражнение на выделение в доказательстве недостающих утверждений и их обоснований

Упражнения на систематизацию теорем

Упражнения на составление плана доказательства теоремы

Упражнения на составление алгоритмов

В целях облегчения запоминания громоздких формулировок теорем целесообразно поэлементное усвоение содержания теоремы. Для этого формулировка теоемы разбивается на отдельные элементы, после чего каждый из элементов используется при выполнении упражнений.

При индуктивном введении теоремы Лященко Е. И. [9] условно выделяет следующие этапы ее изучения:

Мотивация изучения теоремы и раскрытие ее содержания (Усмотрение геометрического факта и формулировка теоремы);
Работа над структурой теоремы;
Мотивация неоходимости доказательства теоремы;
Построение чертежа и краткая запись содержания теоремы;
Поиск доказательства, доказательство и его запись;
Закрепление теоремы;
Применение теоремы.

Для мотивации необходимости изучения теорем можно предложить такие приемы:

Прием 1. Обощение наблюдаемых в жизни фактов и явлений и перевод их на математический язык.

А) На плане местности четыре населенных пункта отмечены точками A,B,C,K. Выясните, пересекутся ли пути из пункта А в пункт С и из пункта K в пункт В. Если пересукуться, то в скольких точках? Рассмотрите различные возможные случаи расположения населенных пунктов. Могут ли эти пути пересечься в двух точках?

В классе учитель выясняет полученные результаты решения задачи: во всех случаях пути движения либо имеют одну общую точку, либо е имеют ни одной. Отметив, что пути движения в данных задачах были отрезки, предпалагается подумать над вопросом: изменится ли вывод, если вместо отрезков взять две прямые?

Этот прием можно использовать при изучении многих теорем.

Прием 2. Показ необходимости знания той или иной теоремы для решения практических задач.

Картографам необходимо нанести на карту два населенных пункта А и В (рис. 7). Измерить расстояние между пунктами оказалось невозможно так как между ними было озеро. Картографы поступили следующим образом: они выбрали точку С от которой

можно было измерить расстояние и до пункта А, и до пункта В. Измерили эти расстояния и построили на бумаге отрезки АС и АВ соответствующей длины (масштаб можно указать по своему усмотрению) а затем продолжили линии за точку С, отложили отрезки СН и СМ, равные соответственно отрезкам СВ и СА, и соединили точки Н и М отрезком. Картографы считают, что расстояние АВ и НМ равны между собой. Правы ли картографы?

- По условию задачи известно, что АС=СМ, ВС=СН и, кроме того как вертикальные углы.

- Надо установить, что АВ=НМ.

- Откуда может следовать равенство этих отрезков?

- Равенство отрезков АВ и НМ может следовать из равенства треугольников АСВ и МСН.

- Но в равных треугольниках соответственно равны все шесть элементов (три стороны и три угла), а здесь мы имеем только две стороны и угол между ними одного треугольника соответственно равные двум сторонам и углу между ними другого треугольника. Как быть?

- Следует доказать, что если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Мотив и необходимость доказательства теоремы показаны.

Прием 3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.

Прием 4. Показ, как решалась данная проблема в истории науки.

Например, рассмотрим доказательство формулы (а + b) 2 = a 2 +2ab +b 2 . У древних греков величины обозначались не числами или буквами, а отрезками прямых. Они говорили не “а 2 ”, а “квадрат на отрезке а”, не “ab”, а “прямоугольник, заключенный между отрезками a и b”.

Первым с доказательством этой формулы столкнулся древнегреческий учёный Евклид, живущий в Александрии в III веке до н.э., так как в те времена не было букв, он пользовался геометрическим способом доказательства формулы.

Из данного рисунка видно, что площадь квадрата со стороной (а + b) равна сумме площадей квадрата со стороной а, квадрата со стороной b и двух прямоугольников с длиной а и шириной b. Если прямая линия (имеется в виду отрезок) разделен на 2 отрезка а и b, то квадрат на всей прямой, т.е. (а + b) 2 равен а 2 + b 2 + 2ab.

Значит, (а + b) 2 = a 2 +2ab +b 2

Очевидно, что перечисленные приемы для мотивации изучения теорем служат одновременно и раскрытию содержания теоремы. Из других приемов раскрытия содержания теорем можно назвать:

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ДОПОЛНИТЕЛЬНОГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ИНСТИТУТ ДИСТАНЦИОННОГО ПОВЫШЕНИЯ КВАЛИФИКАЦИИ

Теорема. Виды теорем. Методика работы над теоремой

слушатель _3.30.1__ курса

Крупко Елена Александровна

к. психол. наук, доц. Шелепанова Н.В.

Введение 3

ВИДЫ ТЕОРЕМ 5

ПРЯМЫЕ ПРИЁМЫ ДОКАЗАТЕЛЬСТВА 8

КОСВЕННЫЕ ПРИЁМЫ ПОИСКА 8

МЕТОДЫ ДОКАЗАТЕЛЬСТВА, ВЫДЕЛЕННЫЕ ПО ИСПОЛЬЗУЕМОМУ МАТЕМАТИЧЕСКОМУ АППАРАТУ 8

ЭТАПЫ ИЗУЧЕНИЯ ТЕОРЕМЫ 8

МЕТОДОЛОГИЧЕСКИЕ ПРИЁМЫ МОТИВИРОВКИ НЕОБХОДИМОСТИ ИЗУЧЕНИЯ ТЕОРЕМ 9

ЗАДАНИЯ, СПОСОБСТВУЮЩИЕ УСВОЕНИЮ ТЕОРЕМ 9

Заключение 10

Литература 10

Теорема – математическое предложение, истинность которого устанавливается посредством доказательства.

Виды формулирования теоремы: импликативная и категорическая.

Условие теоремы – при каких условиях рассматривается в ней тот или иной объект.

Заключение теоремы – что об этом объекте утверждается.

Основные типы теорем:

4. Контрапозитивная (обратная противоположной).

Доказательство – рассуждение с целью обоснования истинности какого-либо утверждения.

Элементы доказательства:

Тезис – математическое предложение, в котором выражается главная цель доказательства. Форма выражения тезиса – суждение.

Аргументы доказательства – положения, на которые опирается доказательство и из которых при условии их истинности необходимо следует истинность доказываемого тезиса. Форма выражения аргументов – суждения.

Демонстрация – логический процесс взаимосвязи суждений, в результате которого осуществляется переход от аргументов к тезису.

Метод доказательства – способ связи аргументов при переходе от условия к заключению суждения.

Методы доказательства, выделенные по тому, как строится обоснование тезиса: прямые и косвенные .

ВИДЫ ТЕОРЕМ

В том случае, если предложение, противоположное данному, будет истинно, его называют теоремой, противоположной данной .

Вообще, для какой бы теоремы мы ни формулировали предложение, обратное противоположному, оно всегда будет теоремой, потому что имеется следующая равносильность: ( АВ) (ВА).

Эту равносильность называют законом контрапозиции.

Теоремы АВ и ВА – взаимообратные, а АВ и – взаимопротивоположные.

Примеры.

ПРЯМЫЕ ПРИЁМЫ ДОКАЗАТЕЛЬСТВА

- синтетический – преобразование условия суждения;

- восходящий анализ – отыскание достаточных оснований справедливости заключения;

- нисходящий анализ – отыскание необходимых признаков справедливости суждения с последующей проверкой обратимости рассуждений;

- последовательное преобразование то условия, то заключения суждения.

КОСВЕННЫЕ ПРИЁМЫ ПОИСКА

- метод от противного – метод, при котором истинность доказываемого тезиса устанавливается посредством опровержения противоречащего ему суждения;

- разделительный метод (метод разделения условий или метод исключения) – метод, при котором тезис рассматривается как один из возможных вариантов предположений, когда все предположения опровергаются, кроме одного.

МЕТОДЫ ДОКАЗАТЕЛЬСТВА, ВЫДЕЛЕННЫЕ ПО ИСПОЛЬЗУЕМОМУ МАТЕМАТИЧЕСКОМУ АППАРАТУ

- Метод геометрических преобразований – метод, используемый как средство обоснования некоторых отношений между элементами евклидовой геометрии.

- Алгебраические методы – методы доказательства теорем с помощью уравнений, неравенств, тождественных преобразований.

- Векторный метод – метод, использующий аппарат векторной алгебры.

- Координатный метод – метод, позволяющий устанавливать переход от геометрических отношений к аналитическим.

ЭТАПЫ ИЗУЧЕНИЯ ТЕОРЕМЫ

- мотивация изучения теоремы и раскрытие ее содержания;

- работа над структурой теоремы;

- мотивация необходимости доказательства теоремы;

- построение чертежа и краткая запись содержания теоремы;

- поиск доказательства, доказательство и его запись;

МЕТОДОЛОГИЧЕСКИЕ ПРИЁМЫ МОТИВИРОВКИ НЕОБХОДИМОСТИ ИЗУЧЕНИЯ ТЕОРЕМ

1. Обобщение наблюдаемых в жизни фактов и явлений и перевод их на математический язык.

2. Показ необходимости знания той или иной теоремы для решения практических задач.

3. Показ необходимости знания той или иной теоремы для решения задач и доказательства других теорем.

4. Показ, как решалась данная проблема в истории науки.

ЗАДАНИЯ, СПОСОБСТВУЮЩИЕ УСВОЕНИЮ ТЕОРЕМ

1) Сформулируйте теорему.

2) Выделите условие и заключение теоремы. К каким фигурам применима теорема?

4) Сформулируйте предложение, обратное теореме.

5) Воспроизведите доказательство теоремы по новому чертежу, изменив его положение и обозначение элементов.

6) Составьте план доказательства.

7) Назовите аргументы, которые использовались при доказательстве.

8) Докажите теорему другим способом.

9) Решите задачи на применение теоремы.

В отличие от других наук, в математике недопустимы эмпирические доказательства: все утверждения доказываются исключительно логическими способами. В математике важную роль играют математическая интуиция и аналогии между разными объектами и теоремами; тем не менее, все эти средства используются учёными только при поиске доказательств, сами доказательства не могут основываться на таких средствах.

Доказательства, написанные на естественных языках, могут быть не очень подробными в расчёте на то, что подготовленный читатель сам сможет восстановить детали. Строгость доказательства гарантируется тем, что его можно представить в виде записи на формальном языке (это и происходит при компьютерной проверке доказательств).

Лернер И.Я. Дидактические основы методов обучения. – М.: Педагогика, 1981. 185 с.

Саранцев Г.И. Теоретические основы методики упражнений по математике в средней школе: Автореф. дисс. … доктора пед. наук.- Л.: Изд-во Ленинградского педуниверситета, 1987. – 36 с.

Саранцев Г.И. Упражнения в обучении математике, т.4. – М.: Просвещение, 1995. – 240 с.

Не только каждый школьник, но и каждый уважающий себя образованный человек должен знать, что такое теорема и доказательство теорем. Может, такие понятия и не встретятся в реальной жизни, но структурировать многие знания, а также делать умозаключения они точно помогут. Именно поэтому мы и рассмотрим в этой статье способы доказательства теорем, а также ознакомимся со столь знаменитой теоремой Пифагора.

Что же такое теорема

Если рассматривать школьный курс математики, то очень часто в нем встречаются такие научные термины, как теорема, аксиома, определение и доказательство. Для того чтобы ориентироваться в программе, нужно ознакомиться с каждым из этих определений. Сейчас же мы рассмотрим, что такое теорема и доказательство теорем.

Итак, теорема – это некое утверждение, которое требует доказательства. Рассматривать данное понятие нужно параллельно с аксиомой, так как последняя доказательства не требует. Ее определение уже является истинным, поэтому воспринимается как должное.

Сфера применения теорем

Ошибочно думать, что теоремы применяются только в математике. На самом деле это далеко не так. Например, существует просто невероятное количество теорем в физике, позволяющих подробно и со всех сторон рассмотреть некоторые явления и понятия. Сюда можно отнести теоремы Ампера, Штейнера и многие другие. Доказательства таких теорем позволяют неплохо разобраться в моментах инерции, статике, динамике, и во многих других понятиях физики.

Использование теорем в математике

Тяжело представить себе такую науку, как математика, без теорем и доказательств. Например, доказательства теорем треугольника позволяют подробно изучить все свойства фигуры. Ведь очень важно разобраться в признаках подобия, свойствах равнобедренного треугольника и во многих других вещах.

Доказательство теоремы площади позволяет понять, как проще всего вычислять площадь фигуры, опираясь на некоторые данные. Ведь, как известно, существует большое количество формул, описывающих, как можно найти площадь треугольника. Но перед тем как их использовать, очень важно доказать, что это возможно и рационально в конкретном случае.

Как доказывать теоремы

Каждый школьник должен знать, что такое теорема, и доказательство теорем. На самом деле доказать какое-либо утверждение не так-то просто. Для этого нужно оперировать многими данными и уметь делать логические выводы. Конечно, если вы неплохо владеете информацией по определенной научной дисциплине, то доказать теорему для вас не составит особого труда. Главное - выполнять процедуру доказательства в определенной логической последовательности.

Для того чтобы научиться доказывать теоремы по таким научным дисциплинам, как геометрия и алгебра, нужно иметь неплохой багаж знаний, а также знать сам алгоритм доказательства. Если вы освоите такую процедуру, то решать математические задачи впоследствии для вас не составит особого труда.

Что нужно знать о доказательстве теорем

Что такое теорема и доказательства теорем? Это вопрос, который волнует многих людей в современном обществе. Очень важно научиться доказывать математические теоремы, это поможет вам в будущем строить логические цепочки и приходить к определенному выводу.

Итак, для того чтобы доказывать теорему правильно, очень важно сделать правильный рисунок. На нем отобразите все данные, которые были указаны в условии. Также очень важно записать всю информацию, которая предоставлялась в задаче. Это поможет вам правильно проанализировать задание и понять, какие именно величины в нем даны. И только после проведения таких процедур можно приступать к самому доказательству. Для этого вам нужно логически выстроить цепочку мыслей, используя другие теоремы, аксиомы или определения. Итогом доказательства должен быть результат, истинность которого не подлежит сомнению.

Основные способы доказательства теорем

В школьном курсе математики существует два способа, как доказать теорему. Чаще всего в задачах используют прямой метод, а также метод доказательства от противного. В первом случае просто анализируют имеющиеся данные и, опираясь на них, делают соответственные выводы. Также очень часто используется и метод от противного. В этом случае мы предполагаем противоположное утверждение и доказываем, что оно неверно. На основе этого мы получаем противоположный результат и говорим о том, что наше суждение было неверным, а значит, указанная в условии информация является правильной.

На самом деле многие математические задачи могут иметь несколько способов решения. Например, теорема Ферма доказательств имеет несколько. Конечно, некоторые рассматриваются только одним способом, но, например, в теореме Пифагора можно рассмотреть сразу несколько из них.

Что представляет собой теорема Пифагора

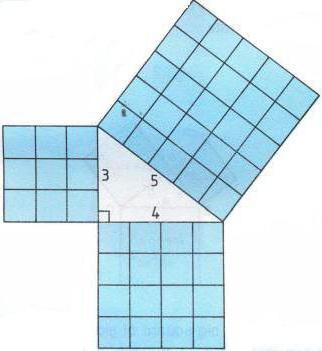
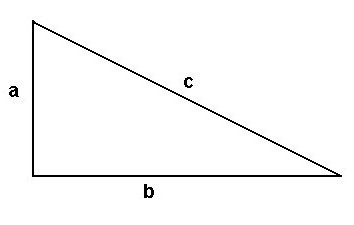
Согласно научным данным, в самом начале рассматривался равносторонний прямоугольный треугольник. Затем строились квадраты на всех его сторонах. Квадрат, построенный на гипотенузе, будет состоять из четырех равных между собой треугольников. В то время как фигуры, построенные на катетах, будут состоять только из двух таких же треугольников. Такое доказательство теоремы Пифагора является самым простым.

Рассмотрим еще одно доказательство данной теоремы. В нем нужно использовать знания не только из геометрии, но также и из алгебры. Для того чтобы доказать данную теорему этим способом, нам нужно построить четыре аналогичных прямоугольных треугольника, и подписать их стороны как а, в и с.

Построить эти треугольники нужно таким образом, чтобы в результате у нас получилось два квадрата. Внешний из них будет иметь стороны (а+в), а вот внутренний – с. Для того чтобы найти площадь внутреннего квадрата, нам нужно найти произведение с*с. А вот для того чтобы найти площадь большого квадрата, нужно сложить площади маленьких квадратов и добавить площади полученных прямоугольных треугольников. Теперь, произведя некоторые алгебраические операции, можно получить такую формулу:

На самом деле существует огромное количество методов доказательства теорем. Перпендикуляр, треугольник, квадрат или любые другие фигуры и их свойства можно рассмотреть с помощью применения различных теорем и доказательств. Теорема Пифагора только является тому подтверждением.

Вместо заключения

Очень важно уметь формулировать теоремы, а также правильно их доказывать. Конечно, такая процедура является достаточно сложной, так как для ее осуществления необходимо не только уметь оперировать большим количеством информации, но также и выстраивать логические цепочки. Математика – это очень интересная наука, которая не имеет ни конца, ни края.

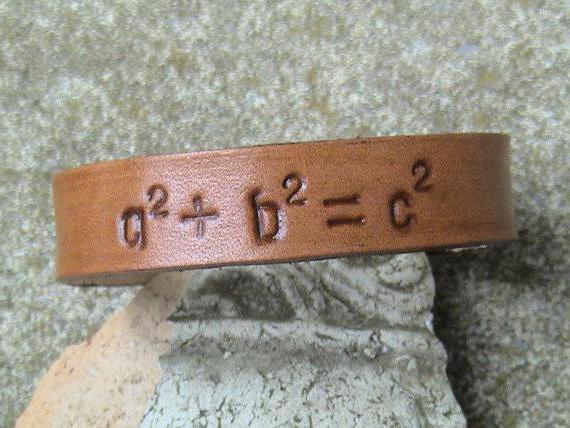
Начните ее изучать, и вы не только повысите уровень своего интеллекта, но и получите огромное количество интересной информации. Займитесь своим образованием уже сегодня. Поняв основные принципы доказательств теорем, вы сможете проводить свое время с большой пользой.

Теорема, виды теорем, структура. Логико-математический анализ теорем. Методические особенности их изучения ( реферат , курсовая , диплом , контрольная )

С точки зрения логики теорема представляет собой высказывание, часто в форме импликации или эквиваленции.

Также в школьном курсе математики, особенно в курсе алгебры, встречаются теоремы-тождества и теоремы-формулы (выраженные языком математических символов), например теоремы о свойствах неравенств, уравнений и многие другие.

Особый вид теорем — это теоремы существования (отсутствуют условие и заключение, но утверждается существование объекта, обладающего определенными свойствами). Обычно после введени я математического понятия необходимо показать, что оно существует. Так, например, после введения определения параллельных прямых необходимо показать их существование. Это можно сделать (если тема перпендикулярности предшествует теме параллельности) через построение непересекающихся прямых на плоскости (две перпендикулярные прямые к одной прямой), а они являются параллельными на плоскости.

Теоремы с доказательствами составляют ядро теории школьного курса математики. В курсе геометрии наиболее распространены теоремы, логическая структура которых представлена в виде импликации или эквиваленции. Структура такой теоремы включает разъяснительную часть, множество объектов, на котором рассматривается теорема, условие, заключение, логические связки.

Заключение

и условие могут состоять из одного простого высказывания, тогда утверждение называют простым, если же условие или заключение состоят из нескольких простых высказываний, то утверждение называют сложным. Работа с такими теоремами предполагает выполнение учителем логико-математического анализа (ЛМА).

Логико-математический анализ теоремы включает:

Анализ формулировки теоремы (А => В) проводится для дальнейшего проведения доказательства. С этой точки зрения полезно сформулировать утверждения:

• обратное данному (условие и заключение исходного утверждения меняют местами): В =>А;
• противоположное данному (к условию и заключению применяют отрицание): 1А => 1 В;
• обратное противоположному или противоположное обратному: 15 => ~|А.

Согласно закону контрапозиции исходное прямое утверждение равносильно противоположному обратному, что используется при доказательстве теорем.

Составление таких утверждений помогает правильно выделить разъяснительную часть теоремы, так как у утверждений обратного, противоположного и обратного противоположному данному утверждению она одинакова.

Итак, выполнение ЛМА предполагает:

• установление формы формулировки;
• перевод, если необходимо, в импликативную форму;
• запись структуры теоремы, т. е. вычленение разъяснительной части, условия, заключения с выделением простых высказываний, и содержания структурных элементов;
• определение вида теоремы (простая или сложная);
• формулирование утверждений: обратного данному, противоположного данному и обратного противоположному. Определение их истинности или ложности.

Формулирование утверждений, обратных и противоположных данному, позволяет уточнить разъяснительную часть.

Логический анализ утверждения представлен в табл. 8.1.

Математический анализ оформим в виде таблицы (табл. 8.2).

Логический анализ утверждения.

Заключение

V (x, у) G М

У (х, у) G М

V (x, у) G М

1 А (х, у)

Обратное противоположному (4).

Таблица 8.2

Математический анализ утверждения.

Разъяснительная часть (М).

Заключение

Множество пар углов.

Их сумма равна 180°.

Множество пар углов.

Сумма углов равна 180°.

Множество пар углов.

Углы нс смежные.

Сумма углов не равна 180°.

Множество пар углов.

Сумма углов не равна 180°.

Углы не смежные.

Этапы работы с теоремой фактически такие же, как и этапы работы с понятием, но содержание некоторых этапов отличается. Поэтому выделим специфику этапов при работе с теоремой.

Профессиональный этап осуществляет учитель сам.

Также на этом этапе учитель отбирает актуализируемые знания и умения для введения как формулировки теоремы, так и доказательства, выделяет идею (идеи) доказательства.

Например, в теореме о сумме углов треугольника одна основная идея метрическая: замена величины одних объектов на такую же величину (численно) другого объекта. Какого? 180° связывается с развернутым углом. Но где его взять? А точнее, прямую, которая его образует и позволит составить сумму углов треугольника. Отсюда другая внутридисциплинарная идея связана со свойствами параллельных прямых. И она как раз и объясняет выбор прямой, параллельной одной из сторон треугольника, на этапе дополнительного построения при проведении доказательства. Конечно, выделение идеи происходит при доказательстве уже на этапе поиска способа доказательства.

Подготовительный этап включает следующие подэтапы:

• актуализация знаний и умений, выделенных на профессиональном этапе;
• мотивация необходимости изучения факта;
• подведение к теоретическому факту.

Эти три подэтапа часто осуществляются на уроке одновременно. Как и при работе с понятием, они могут быть реализованы через демонстрацию использования факта в окружающем мире. Например, почему чаще всего пешеходный переход прокладывают перпендикулярно тротуару (для теоремы о перпендикуляре и наклонной к одной прямой).

Также может быть предложена предметная проблемная ситуация через возможность решения какой-либо задачи, если было бы истинно утверждение (теорема). Еще одним приемом может быть использование софизма, построенного на невыполнении утверждения (теорема). Может быть организована практическая работа, например, при введении теоремы о сумме углов треугольника предлагается вырезать треугольник, а далее найти сумму его углов, просто отрезав их и сложив вместе. Далее выдвигается гипотеза, что сумма углов треугольника, возможно, равна 180°.

Основной этап:

Поиск способа доказательства может быть организован по-разному. Он может быть осуществлен уже на подготовительном этапе при подведении к теоретическому факту.

Пример

При введении теоремы о признаке перпендикулярности прямой и плоскости на подготовительном этапе можно предложить учащимся рассмотреть ситуацию. Нам надо поставить палатку. У нее есть центральный стержень, на который будет крепиться палатка. Как он должен быть расположен по отношению к поверхности, на которой располагается палатка? Да, перпендикулярно. Предложите способы его установки. Ученики предлагают: прикрепив веревки к его вершине, натянем их, привязав к колышкам, вбитым в землю. Два колышка хватит? Выясняем, что нет, так как стержень будет вращаться в одной полуплоскости. Тогда предлагают еще два колышка, чтобы стержень стоял перпендикулярно поверхности. Каждая пара колышков, как две точки, задаст прямую. Таким образом, выходим на теоретический факт и способ доказательства через построение равнобедренных треугольников, медианой и высотой которых является отрезок (центральный стержень).

Схема доказательства или поисковая схема выполняется так же, как в теме о задачах, так как доказательство теоремы — это фактически решение задачи на доказательство.

Читайте также: