Теорема гаусса маркова реферат

Обновлено: 05.07.2024

Для того чтобы регрессионный анализ, основанный на обычном методе наименьших квадратов, давал наилучшие из всех возможных результаты, случайная ошибка должна удовлетворять определенным условиям, известным как условия Гаусса-Маркова.

Понимание важности этих условий отличает компетентного исследователя от некомпетентного. Если условия не выполнены, надо это осознавать. А именно, если возможно, то провести корректирующие действия; если невозможно корректировка, то оценить, как невыполнение условий влияет на результат.

1-е условие Гаусса-Маркова состоит в том, что математическое ожидание случайной ошибки в любом наблюдении должно быть равно нулю:

Это означает, что иногда случайная ошибка будет положительной, иногда отрицательной, но она не должна иметь систематического смещения. Фактически, если уравнение регрессии включает свободный член, то разумно предположить, что это условие выполнено автоматически, так как роль константы состоит в определении любой систематической тенденции объясняемой переменной, которую не учитывают объясняющие переменные, включенные в уравнение регрессии.

Таким образом, если уравнение регрессии включает постоянную , то именно константа содержит информацию о систематической тенденции в y. Поэтому 1-ое условие можно считать всегда выполненным.

В терминах зависимой переменной условие означает, что ,то есть при фиксированном х_i среднее значение y_i лежит на линии регрессии и равно .

2-е условие Гаусса-Маркова состоит в том, что дисперсия ошибки постоянна для всех наблюдений:

Условие независимости дисперсии от номера наблюдения называется гомоскедастичностью (homoscedasticity). Случай непостоянства дисперсии для разных наблюдений называется гетероскедастичностью (heteroscedasticity). На рис.5 а) приведен пример типичной картинки для случая гомоскедастичности ошибок, на рис. 5 б) – пример данных с гетероскедастичными ошибками.

а) гомоскедастичность ошибок

б) гетероскедастичность ошибок

Рисунок 4 – Принципиальные схемы случаев гомоскедастичности и гетероскедастичности ошибок

Иногда случайная ошибка будет больше, иногда меньше, однако не должно быть такого, что в одних наблюдениях ошибка систематически больше, чем в других. Эта постоянная дисперсия обозначается σ 2 _.

В терминах зависимой переменной условие гомоскедастичности формулируется как условие постоянства дисперсии y: D(y)=σ 2 .

Если условие постоянства дисперсии не выполняется, то оценки, найденные по методу наименьших квадратов, будут неэффективны. Для получения более надежных результатов надо использовать модифицированный метод наименьших квадратов (см., например, Доугерти, 2001).

Величина σ 2 неизвестна. Одна из задач регрессионного анализа состоит в ее оценке, точнее оценке стандартного отклонения случайного члена.

3-е условие Гаусса-Маркова - условие некоррелированности ошибок - состоит в том, что предполагается отсутствие систематической связи между значениями случайной ошибки в любых двух наблюдениях:

Например, если случайная ошибка в одном наблюдении велика и положительна, то это не должно обусловливать систематическую тенденцию к тому, что в следующем наблюдении она будет обязательно мала и отрицательна (или велика и отрицательна, или мала и положительна). Случайные ошибки должны быть абсолютно независимы друг от друга, то есть ковариация между ними должна быть равна нулю.

Это условие часто нарушается в случае, когда наши данные являются временными рядами. В случае, когда условие некоррелированности ошибок не выполняется, то говорят об автокорреляции ошибок.

Типичная картинка автокорреляции ошибок представлена на рис. 6.

В терминах зависимой переменной условие отсутствия автокорреляции означает статистическую независимость значений y для разных наблюдений: cov(y_i, y_j)=0, i≠j.

Если третье условие не выполнено, то регрессия, оцененная методом наименьших квадратов, даст неэффективные результаты. Методы получения более надежных результатов представлены, например, в учебнике Кристофера Доугерти (2001).

а) ковариация ошибок положительна

б) ковариация ошибок отрицательна

Рисунок 5 – Принципиальные схемы автокорреляции ошибок

4-е условие Гаусса-Маркова – случайная ошибка должна быть распределена независимо от объясняющих переменных.

Значение объясняющей переменной x в каждом наблюдении должно считаться экзогенным, полностью определяемым внешними причинами, не учитываемыми в уравнении регрессии.

Во многих случаях используется более сильное условие: объясняющие переменные не являются стохастическими.

Предположение о нормальности распределения ошибок часто используется одновременно с условиями Гаусса-Маркова:

Ошибки u_i имеют совместное нормальное распределение с параметрами: математическое ожидание – 0, дисперсия – σ 2 .

В терминах зависимой переменной условие нормальности распределения ошибок означает, что значения y также распределены по нормальному закону с параметрами: математическое ожидание – 0, дисперсия – σ 2 .

При соблюдении перечисленных пяти условий регрессионная модель (41) называется классической нормальной линейной регрессионной моделью.

В предположениях классической линейной регрессии модели:

1) - спецификация модели,

где x – неслучайная величина; y, u – случайные величины.

оценки а и b для параметров α и β, полученные по методу наименьших квадратов, имеют наименьшую дисперсию среди всех линейных несмещенных оценок, то есть аиb несмещенные эффективные оценки.

Таким образом, оценки а и b являются наилучшими в статистическом смысле.

4.6.3. Оценка дисперсии ошибок σ 2

Имеем - прогноз y_i в точке x_i.

Тогда . Здесь, как и прежде, e_i – остатки.

Не следует путать остатки e_i с ошибками u_i. Остатки тоже случайные величины, однако остатки e_i наблюдаемы в отличие от ошибок u_i.

Можно доказать, что - оценка дисперсии ошибок σ 2 определяется через сумму квадратов остатков по формуле:

Величина s 2 являются несмещенной оценкой дисперсии ошибок σ 2 .

Квадратный корень из s 2 , то есть величина s называется стандартной ошибкой оценки .

4.6.4. Оценка дисперсий параметров модели a и b

Уравнение множественной регрессии. Теорема Гаусса – Маркова ( реферат , курсовая , диплом , контрольная )

Почему же в практических приложениях оказались важными свойства оценок? Это связано с тем, что при моделировании реальных объектов, в том числе экономических, параметры являются не только числовыми коэффициентами при переменных, а несут на себе смысловую нагрузку, часто имеют размерность и по их величинам делают вывод о свойствах объекта.

Например, если модель (2.8) описывает зависимость расходов на потребление от располагаемого дохода, то параметр a1 есть предельные расходы по доходу и показывает, на сколько единиц изменяются расходы на потребление при увеличении дохода на одну единицу.

Теорема Гаусса — Маркова [1] формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

Несмотря на то, что Марков родился через год после смерти Гаусса, теорема была названа по их именам. Заслуга Гаусса — в разработке МНК, заслуга Маркова — в формулировке условий, при которых МНК позволяет получить состоятельные оценки.

Сформулируем постановку задачи. Мы имеем:

1) спецификацию модели в виде линейного уравнения множественной регрессии:

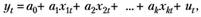
(5.20).

2) выборку из n наблюдений за поведением переменных модели:

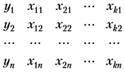
(5.21).

Значения переменных в каждом наблюдении связаны между собой по правилу (5.20). Следовательно, в соответствие каждому наблюдению можно поставить уравнение:

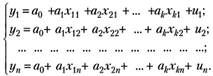
(5.22).

Система уравнений (5.22) называется системой уравнений наблюдения или схемой Гаусса — Маркова.

Далее будем использовать следующие обозначения.

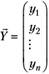
- вектор наблюдений за эндогенной переменной; (5.23).

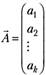
- вектор параметров линейной модели; (5.24).

(5.25).

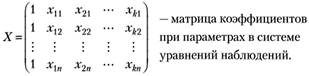
В матрице X в первом столбце записана единица.

В компактной записи с учетом введенных обозначений система уравнений наблюдений (схема Гаусса — Маркова) имеет вид:

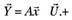
(5.26).

Задача заключается в том, чтобы найти:

1) значения состоятельных оценок параметров модели (5.20);
2) значения несмещенных ошибок оценок параметров;
3) оценку ошибки случайного возмущения;
4) оценку наилучшего прогноза с помощью модели (5.20);
5) оценку ошибки прогноза.

Теорема начинается с описания условий, которые накладываются на вектор случайных возмущений. Эти условия принято называть предпосылками теоремы Гаусса — Маркова.

Теорему условно можно разбить на две части: " если" и " тогда" .

1. Математическое ожидание случайных возмущений во всех наблюдениях равно нулю:

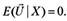
(5.27).

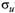
2. Дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе :

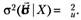
(5.28).

3. Ковариация между парами случайных возмущений в наблюдениях равны нулю (случайные возмущения в наблюдениях независимы):

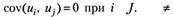
(5.29).

4. Ковариация между вектором регрессоров и вектором случайных переменных равна нулю (регрессоры и случайные возмущения независимы):

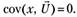
(5.30).

" Тогда" : если матрица X (5.26) неколлинеарная (нет ни одного столбца, который можно было бы представить в виде линейной комбинации других его столбцов).

1. Наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется, как.

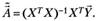
(5.31).

Она соответствует методу наименьших квадратов.

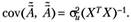
(5.32).

3. Дисперсия случайного возмущения равна.

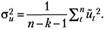
(5.33).

4. Наилучший прогноз по модели (5.20) в точке.

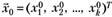
вычисляется по правилу:

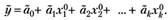
(5.34).

5. Ошибка прогноза эндогенной переменной равна.

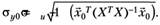
(5.35).

Учитывая важность теоремы Гаусса — Маркова для эконометрики, рассмотрим ее доказательство.

Доказательство. Воспользуемся методом наименьших квадратов:

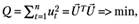
(5.36) где.

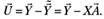
(5.37).

Подставляя (5.37) в (5.36) и выполнив перемножения, получим:

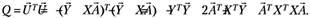
(5.38).

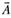
Для получения необходимого условия экстремума дифференцируем (5.38) по вектору :

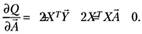
(5.39).

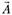
Отсюда, система нормальных уравнений для вычисления оценок вектора имеет вид:

(5.40).

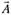
Тогда оценка вектора есть.

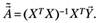
Выражение (5.31) доказано.

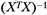
Замечание. Требование неколлинеарности матрицы X обеспечивает существование матрицы . В противном случае процедура (5.31) неосуществима.

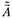
Покажем, что процедура (5.31) дает несмещенную оценку параметров модели множественной регрессии. Для этого необходимо вычислить математическое ожидание вектора оценки :

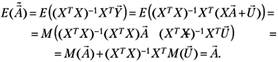
(5.41).

Таким образом, несмещенность оценки (5.31) доказана. Отметим, что несмещенность достигнута в силу выполнения первой предпосылки теоремы Гаусса — Маркова.

Аналогичным образом доказывается справедливость выражения (5.32).

Остановимся более подробно на предпосылках теоремы Гаусса — Маркова.

Первая предпосылка (5.27) говорит о том, что во всех наблюдениях среднее значение (математическое ожидание) случайного возмущения равно нулю. Эта предпосылка отвечает за несмещенность параметров линейной модели множественной регрессии. Именно выполнение этой предпосылки обеспечило равенство нулю второго слагаемого в (5.41) и позволило получить несмещенные параметры модели.

Вторая предпосылка теоремы требует, чтобы во всех наблюдениях дисперсия случайного возмущения была одинаковой. Это свойство получило название свойства гомоскедастичности или однородности, или одинаковости дисперсий. В случае невыполнения данного условия говорят, что случайные возмущения в уравнениях наблюдения гетероскедастичные или неоднородные. Если случайные возмущения гетероскедастичные, то оценки параметров модели остаются несмещенными, но теряется эффективность оценки дисперсий параметров. Они, как правило, оказываются завышенными.

Третья предпосылка теоремы требует независимости случайных возмущений. Другими словами, каким бы не оказалось значение случайного возмущения в первом наблюдении, оно никак не сказывается на значениях случайного возмущения в любом другом наблюдении. Это свойство получило название неавтокоррелируемости случайных возмущений. Если это свойство не выполняется, то это так же сказывается на оценках дисперсий параметров модели. В этом случае дисперсии, как правило, занижены.

Четвертая предпосылка теоремы требует независимости случайных возмущений от значений регрессоров (экзогенных переменных). Как мы уже отмечали, рассматривая результат построения модели парной регрессии (5.9), невыполнение этого условия приводит к смещенности параметров модели. В тех случаях, когда значения регрессоров фиксированы, т. е. являются константами, эта предпосылка выполняется автоматически. Однако в ряде случаев регрессоры могут носить случайный характер. Например, если значения регрессоров в выборке есть результат измерений, или когда в качестве регрессора выступает лаговая эндогенная переменная.

Вопрос 1. Теорема Гаусса-Маркова для линейной модели парной регрессии.

Уравнение линейной модели парной регрессии: Y = b0 + b1X.

Предпосылки МНК (условия Гаусса−Маркова)

10 Математическое ожидание случайного отклонения εi равно нулю: M(εi) = 0 для всех наблюдений.

Данное условие означает, что случайное отклонение в среднем не оказывает влияния на зависимую переменную. В каждом конкретном наблюдении случайный член может быть либо положительным, либо отрицательным, но он не должен иметь систематического смещения.

20 Дисперсия случайных отклонений εi постоянна: D(εi) = D(εj) = σ2 для любых наблюдений i и j.

Данное условие подразумевает, что несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть либо большим, либо меньшим, не должно быть некой априорной причины, вызывающей большую ошибку (отклонение).

Выполнимость данной предпосылки называется гомоскедастичностью (постоянством дисперсии отклонений). Невыполнимость данной предпосылки называется гетероскедастичностью (непостоянством дисперсий отклонений).

30 Случайные отклонения εi и εj являются независимыми друг от друга для i≠j.

Выполнимость данной предпосылки предполагает, что отсутствует систематическая связь между любыми случайными отклонениями. Другими словами, величина и определенный знак любого случайного отклонения не должны быть причинами величины и знака любого другого отклонения.

40 Случайное отклонение должно быть независимо от объясняющих переменных.

Обычно это условие выполняется автоматически при условии, что объясняющие переменные не являются случайными в данной модели.

50 Модель является линейной относительно параметров.

Если предпосылки 10 − 50 выполнены, то оценки, полученные по МНК, обладают следующими свойствами:

1. Оценки являются несмещенными, т. е. M(b0) = b0 , M(b1) = b1.

Это вытекает из того, что M(εi) = 0 и говорит об отсутствии систематической ошибки в определении положения линии регрессии.

2. Оценки состоятельны, т. к. дисперсия оценок параметров при возрастании числа n наблюдений стремится к нулю.

3. Оценки эффективны, т. е. они имеют наименьшую дисперсию по сравнению с любыми другими оценками данных параметров, линейными относительно величин yi.

Вопрос 2. Проверка нулевой гипотезы и доверительные интервалы для одного из коэффициентов множественной регрессии.

Значимость коэффициента регрессии bj осуществляется с помощью проверки нулевой гипотезыH0 о равенстве параметра нулю.

Выдвигается гипотеза Н0: (коэффициент не значим) и альтернативная ей Н1: (коэффициент значим). Выбирается уровень значимости .

Рассчитывается величина , где - среднее квадратическое отклонение (стандартная ошибка) коэффициента регрессии bj.

Далее определяется табличное значение t – критерия Стьюдента при уровне значимости и числе степеней свободы к=n-р-1.

Если , то гипотезу Н0 принимаем, в противном случае принимаем альтернативную гипотезу о значимости коэффициента регрессии.

В общей постановке вопроса гипотеза Н0 о равенстве параметра заданному числу , т.е. = , отвергается, если .

Поэтому доверительный интервал для параметра есть

В результате регрессии у на 3 независимых переменных, включая константу, по 15 наборам значений (хi1=1,xi2,xi3,yi) получены следующие оценки: , Известна матрица

Проверить гипотезу Н0: b3=1 на 5% - уровне значимости.

Найдем оценку ковариации матрицы: ,

Дисперсия параметров множественной модели определяются соотношением: , т.е. это элементы, лежащие на главной диагонали.

Для проверки значимости гипотезы Н0: b3=1 нужно рассчитать величину: и сравнить ее с теоретической величиной .

Если , то гипотеза Н0 верна, в противном случае гипотезу следует отвергнуть.

Так. как , то гипотезу Н0 следует отвергнуть и принять гипотезу Н1: b3 1.

1. Магнус Я.Р., Катышев П.К., Пересецкий А.А., Эконометрика. Начальный курс., М.: Дело, 2005.

2. Артамонов Н. В. Введение в эконометрику : курс лекций. – М. МЦНМО, 2011.

3. Демиденко Е.З. Линейная и нелинейная регрессии. – М.:Финансы и статистика, 1981.

4. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов. – М.: ЮНИТИ – ДАНА, 2002.

5. Бородич С.А. Эконометрика: Учебное пособие. – Минск: Новое знание, 2001.

6. Елисеева И.И. Эконометрика: Учебник для вузов. – М.: Финансы и статистика, 2002.

2.3. Статистические свойства оценок метода наименьших квадратов

2.3.1. Теоретические предпосылки, на основе которых строятся МНК - оценки, их роль и правдоподобность выполнения в реальных практических задачах

Поскольку полученные оценки a и b коэффициентов линейной регрессии основаны на статистических данных и являются случайными величинами, то естественно установить свойства этих оценок, как случайных величин. Более того, не выяснив этих свойств, невозможно сделать обоснованных выводов относительно качества и надежности полученных оценок. Необходимо, в частности, определить такие их статистические характеристики, как математическое ожидание и дисперсия. К желательным свойствам оценок относятся также несмещенность и состоятельность. Далее, если бы удалось определить вид распределения (плотности распределения) оценок, можно было бы построить доверительные интервалы для истинных значений параметров регрессии (то есть получить интервальные оценки коэффициентов) и реализовать процедуры проверки гипотез относительно их значений. Важную роль играет также изучение статистических свойств остатков оцененной регрессии.

Все эти задачи можно решить, основываясь на некоторых правдоподобных теоретических предпосылках (гипотезах) модели, выполнение которых на практике подлежит проверке с помощью специально разработанных для этого статистических процедур.

Предположение относительно независимых переменных

В дальнейшем будем предполагать, что x - детерминированная (неслучайная) величина, то есть значения независимых переменных заранее известны. Данное предположение (предпосылка), к сожалению, на практике при моделировании реальных социально-экономических процессов часто не выполняется. Это связано с тем, что здесь в качестве независимых переменных часто выступают стохастические неконтролируемые величины, такие как интенсивность потока покупателей в примере гл. 1 или рыночный индекс в рыночной модели, который также является случайной величиной. При нарушении этой предпосылки ряд "хороших" свойств оценок сохраняется (при некоторых условиях), но в ряде случаев требуется корректировка модели (оценок). Обобщения классической модели, которые учитывают нарушение этой предпосылки, будут рассмотрены в гл. 4 .

Предположения относительно случайной составляющей модели

При выполнении предпосылки относительно переменной x статистические свойства оценок параметров и зависимой переменной, а также остатков, целиком определяются вероятностными свойствами случайной составляющей регрессионной модели. Относительно случайной составляющей в классическом регрессионном анализе предполагают выполнение следующих условий, которые называются условиями Гаусса-Маркова и играют ключевую роль при изучении свойств оценок, полученных по методу наименьших квадратов.

1. Первое условие заключается в том, что математическое ожидание случайной составляющей во всех наблюдениях должно быть равно нулю. Формально это записывается так

, для всех t =1,2,…,n.

Смысл этого условия заключается в том, что не должно быть систематического смещения случайной составляющей. В линейной регрессии систематическое смещение линии регрессии учитывается с помощью введения параметра смещения и поэтому данное условие можно считать всегда выполненным.

2. Дисперсия случайной составляющей постоянна для всех наблюдений (то есть не зависит от номера наблюдения). Это условие записывается так

, где дисперсия - величина постоянная.

Это свойство дисперсии ошибок называется гомоскедастичностью (однородностью) (запомните этот термин).

Выполнение условия гомоскедастичности при построении конкретных эконометрических моделей необходимо проверять с помощью специальных статистических процедур. Поскольку истинные дисперсии ошибок неизвестны, их можно лишь приближенно оценить на основе наблюдаемых (точнее - вычисляемых) значений остатков модели в каждом наблюдении. Таким образом, и свойство гомоскедастичности на практике проверяется (диагностируется) на самом деле для остатков модели, а не для истинных ошибок и может выполнятся лишь приближенно. Если условие гомоскедастичности не выполнено (то есть дисперсия ошибок не постоянна), то говорят, что имеет место условие гетероскедастичности (запомните этот термин). Понятия гомоскедастичности и гетероскедастичности являются ключевыми в эконометрике.

Графическая иллюстрация понятий гомоскедастичность и гетероскедастичность

Рис. 2.6а. Гомоскедастичность

Рис. 2.6б. Гетероскедастичность

Рис. 2.6в. Гетероскедастичность

3. Случайные составляющие модели для различных наблюдений некоррелированы. Это условие записывается таким образом

, для всех i не равных j (i, j=1,2,…,n).

Выполнение этого условия означает отсутствие систематической (статистической) связи между значениями случайного члена в любых двух наблюдениях. Это свойство на практике также проверяется с помощью статистических процедур на основе анализа остатков модели. Если оно нарушается, то процедура оценки параметров должна быть скорректирована.

4. Четвертое условие Гаусса-Маркова записывается так

, для всех i и j,

и означает, что объясняющие переменные и случайные составляющие некоррелированы для всех наблюдений. Ранее мы предположили, что объясняющая переменная в модели не является стохастической. В этом случае четвертое условие выполняется автоматически.

Регрессионная модель с детерминированными регрессорами, удовлетворяющая предпосылкам Гаусса-Маркова, называется классической регрессионной моделью .

Дополнительное предположение о нормальном распределении ошибок

При выполнении условий Гаусса-Маркова, оценки наименьших квадратов обладают такими свойствами, как несмещенность , состоятельность и оптимальность (эффективность). Однако, для построения доверительных интервалов и проверки гипотез относительно истинных значений параметров, необходимо дополнительное предположение о распределении случайной составляющей u. В классическом регрессионном анализе предполагается, что эта составляющая распределена по нормальному закону и тогда модель называют классической нормальной линейной регрессией .

Данное предположение является, пожалуй, наиболее спорным. Дело в том, что предположение о нормальности можно считать правдоподобным, если значения случайной величины порождаются в результате воздействия большого количества независимых случайных факторов, каждый из которых не обязательно имеет нормальное распределение. Примером такого воздействия является так называемое броуновское движение (хаотичное движение малых частиц в жидкости как результат совокупного воздействия на частицу (ударов, соударения) большого количества молекул жидкости).

В экономических процессах распределения случайных величин, как правило, отличаются от нормального, поскольку механизм их порождения более сложный, однако чаще всего именно нормальное распределение используется в эконометрических исследованиях (как, впрочем, и в статистике). Это обусловлено следующими причинами. Во - первых, нормальный закон действительно часто достаточно хорошо (с приемлемой для практики точностью) аппроксимирует (приближенно описывает) распределение случайной составляющей. Во - вторых, что очень важно, на основе нормального распределения можно получить удобные для расчетов и применения на практике процедуры проверки гипотез и построения доверительных интервалов. В любом случае, не изучив базовые результаты (процедуры), основанные на предположении нормальности, нельзя продвигаться на более высокий уровень изучения и применения более реалистичных моделей, не использующих эту предпосылку и позволяющих получать более точные результаты.

Если случайные величины в модели распределены по нормальному закону, то из свойств некоррелированности в третьем и четвертом условиях Гаусса-Маркова следует и независимость соответствующих случайных величин.

2.3.2. Свойства выборочных вариаций и ковариаций. Остаточные ошибки (остатки) модели, их свойства

Свойства выборочных вариаций (дисперсий) и ковариаций

Для дальнейшего изложения нам понадобиться установить ряд правил, которые можно использовать при преобразовании выражений, содержащих выборочные вариации и ковариации.

Пусть a - некоторая постоянная, а x, y, z - переменные, принимающие в i-м наблюдении значения x_i, y_i, z_i, i=1,2,3. n (n - количество наблюдений). Тогда можно рассматривать как переменную, значения которой в i-м наблюдении равно a, и

Читайте также: