Степень с натуральным показателем 7 класс реферат

Обновлено: 05.07.2024

Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика: Что такое степень с натуральным показателем

Что такое степень с натуральным показателем

Одна из особенностей математического языка, которым мы с вами должны научиться пользоваться, состоит в стремлении применять как можно более короткие записи. Математик не будет писать a + a + a + a + a, он напишет 5а; не будет писать a + a + a + a + a + a + a + a + a + a (здесь 10 слагаемых), а напишет 10а;
не будет писать
а напишет n а .

Точно так же математик не будет писать 2 • 2 • 2 • 2 • 2, а воспользуется специально придуманной короткой записью . Аналогично вместо произведения семи одинаковых множителей 3 • 3 • 3 • 3 • 3 • 3 • 3 он запишет . Конечно, в случае необходимости он будет двигаться в обратном направлении, например, заменит короткую запись более длинной 2 • 2 • 2 • 2 • 2 • 2, произведет вычисления, получит 64 и запишет

Еще одна особенность математического языка: если появляется новое обозначение, то появляются и новые термины. И все это (и обозначения, и термины) охватываются новым определением.

Определением обычно называют предложение, разъясняющее суть нового термина, нового слова, нового обозначения. Просто так определения не придумываются, они появляются только тогда, когда в этом возникает необходимость.

Определение 1. Под , где n = 2, 3, 4, 5, . понимают произведение n одинаковых множителей, каждым из которых является число а. Выражение называют степенью, число а — основанием степени, число n — показателем степени.

В дальнейшем вы узнаете, что показателем степени может быть не только натуральное число. Но это произойдет позднее, в старших классах, а пока ограничимся только случаем, когда показатель степени — натуральное число; обычно говорят короче: натуральный показатель, отсюда и происходит название как всей главы, так и этого параграфа.

Пример 1. Записать в виде степени произведение 5 • 5 • 5 • 5 • 5 • 5 и использовать соответствующие термины.

Решение. Поскольку дано произведение шести одинаковых множителей, каждый из которых равен 5, имеем:
5 • 5 • 5 • 5 • 5 • 5 = ;
— степень;
5 — основание степени;
6 — показатель степени.

Пример 2. Вычислить

Решение. = (-2) • (-2) • (-2) • (-2) =

Определение 2. Степенью числа а с показателем 1 называют само это число:

Пример 4. Найти значение степени при заданных значениях а и n:

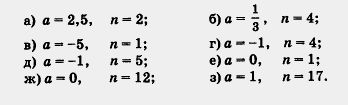
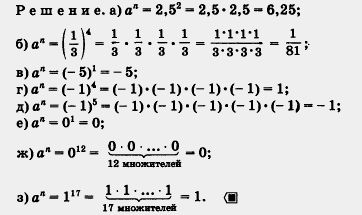
Операцию отыскания степени называют возведением в степень. В примере 4 мы рассмотрели восемь случаев возведения в степень.

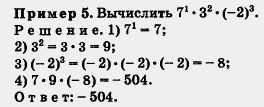
В рассмотренных примерах мы несколько раз возводили в степень отрицательные числа. Заметили ли вы закономерность: если отрицательное число возводится в четную степень, то получается положительное число, если же отрицательное число возводится в нечетную степень, то получается отрицательное число? Попробуйте объяснить, почему это так.

_{Календарно-тематическое планирование по математике, задачи и ответы школьнику онлайн, курсы учителю по математике скачать}

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.

Степени. Свойства степеней.

Ключевые слова конспекта: степень с натуральным показателем, основание степени, показатель степени, возведение в степень, дисперсия, умножение и деление степеней, свойства степеней.

Умножим 7 5 на 7 3 :
7 5 • 7 3 = (7 • 7 • 7 • 7 • 7) • (7 • 7 • 7) = 7 • 7 • 7 • 7 • 7 • 7 • 7 • 7 = 7 8 .
Показатель степени увеличился на 3. Естественно считать, что 7 = 7 1 . Вообще считают, что первой степенью числа является само число. Например, 18 1 = 18; 104 1 = 104.

Степень с натуральным показателем

✅ Определение. Степенью числа а с натуральным показателем n, большим 1, называют выражение а n , равное произведению n множителей, каждый из которых равен а.
Степенью числа а с показателем 1 называют выражение а 1 , равное а.

По определению

Возведение в степень

Нахождение n-й степени числа а называют возведением в n-ю степень.

Пример 1. Возведём число –3 в четвёртую и пятую степени:
(–3) 4 = (-3) • (-3) • (-3) • (-3) = 81;
(–3) 5 = (-3) • (-3) • (-3) • (-3) • (-3) = –243.

Из свойств умножения следует, что:

при возведении нуля в любую степень получается нуль;
при возведении положительного числа в любую степень получается положительное число;
при возведении отрицательного числа в степень с чётным показателем получается положительное число, а при возведении отрицательного числа в степень с нечётным показателем — отрицательное число.

Пример 2. Возведём число 6,1 в седьмую степень, воспользовавшись калькулятором. Для этого надо выполнить умножение:
6,1 • 6,1 • 6,1 • 6,1 • 6,1 • 6,1 • 6,1.
Калькулятор позволяет выполнять возведение в степень проще, не повторяя основание степени и знак умножения. Для того чтобы возвести число 6,1 в седьмую степень, достаточно ввести число 6,1, нажать клавишу УМНОЖИТЬ и шесть раз нажать клавишу РАВНО . Получим, что 6,1 7 = 314274,28.

При вычислении значений числовых выражений, не содержащих скобки, принят следующий порядок действий: сначала выполняют возведение в степень, затем умножение и деление, далее сложение и вычитание.

Пример 3. Найдём значение выражения –6 2 + 64 : (–2) 5 . Последовательно находим:
1) 6 2 = 36;
2) (–2) 5 = –32;
3) 64 : (–32) = –2;
4) –36 + (–2) = –38.

Пример 4. Найдём множество значений выражения 5 • (–1) n + 1 + 2, где n ∈ N.
Если n — нечётное число, то (-1) n + 1 = 1; тогда 5 • (-1) n + 1 + 2 = 5 • 1 + 2 = 7.
Если n — чётное число, то (-1) n + 1 = -1; тогда 5 • (-1) n + 1 + 2 = 5 • (-1) + 2 = -5 + 2 = -3.
Множество значений данного выражения: .

В рассмотренном примере было указано, что n ∈ N. Условимся в дальнейшем такое указание опускать и считать, что если показатель степени содержит переменную, то значениями этой переменной являются натуральные числа.

Дисперсия

Степень с натуральным показателем широко используется в естествознании для вычисления различных характеристик. Например, в статистике, для того чтобы узнать, как числа некоторой выборки расположены по отношению к среднему арифметическому этой выборки, используют отклонения, их квадраты и среднее арифметическое квадратов отклонений — дисперсию.

Пример 5. Дана выборка: 4, 6, 7, 8, 10. Среднее арифметическое этой выборки равно 7. Тогда отклонения вариант данной выборки от среднего арифметического равны: 4 – 7 = –3, 6 – 7 = –1, 7 – 7 = 0,8 – 7 = 1, 10 – 7 = 3, т. е. мы получили ещё один набор чисел — отклонения каждой варианты выборки от среднего арифметического. По новой выборке (–3; –1; 0; 1; 3) можно судить о том, насколько близки к среднему арифметическому числа исходного набора. Но поскольку сумма отклонений равна нулю, то и среднее арифметическое этой новой выборки также равно нулю. Поэтому для дальнейших исследований исходного набора находят квадраты отклонений и их среднее арифметическое

Полученное число и есть дисперсия исходной выборки.

Умножение степеней

Представим произведение степеней а 5 и а 2 в виде степени:
а 5 • а 2 = (а • а • а • а • а) • (а • а) = а • а • а • а • а • а • а = а 7 .
Мы получили степень с тем, же основанием и показателем, равным сумме показателей множителей. Подмеченное свойство выполняется для произведения любых двух степеней с одинаковыми основаниями.

Если а — произвольное число, m и n — любые натуральные числа, то а m • а n = а m+ n

Из основного свойства степени следует правило:

чтобы перемножить степени с одинаковыми основаниями, надо основание оставить тем же, а показатели степеней сложить.

Деление степеней

Представим теперь в виде степени частное степеней а 8 и а 3 , где а ≠ 0. Так как а 3 • а 5 = а 8 , то по определению частного а 8 : а 3 = а 5 .

Мы получили степень с тем же основанием и показателем, равным разности показателей делимого и делителя. Такое свойство выполняется для частного любых степеней с одинаковыми основаниями, не равными нулю, у которых показатель делимого больше показателя делителя.

Если а — произвольное число, не равное нулю, m и n — любые натуральные числа, причём m > n, то а m : а n = а m — n , где а ≠ 0, m ≥ n

Докажем это. Умножим а m — n на а n , используя основное свойство степени:
a m – n • a n = a (m – n) + n = a m – n + n = a m

Из доказанного свойства следует правило:

чтобы выполнить деление степеней с одинаковыми основаниями, надо основание оставить тем же, а из показателя делимого вычесть показатель делителя.

Степень с нулевым показателем

Мы рассматривали степени с натуральными показателями. Введём теперь понятие степени с нулевым показателем.

✅ Определение. Степенью числа а, где а ≠ 0, с нулевым показателем называется выражение а 0 , равное 1 .

Например, 5 0 = 1; (–6,3) 0 = 1. Выражение 0 0 не имеет смысла.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Выберите документ из архива для просмотра:

Выбранный для просмотра документ проект Балашова.docx

Введение.

Проект направлен на расширение, систематизирование и обобщение материала по данной теме.

Одной из основных задач, стоящих перед школой, является выяснение многообразных применений школьного курса математики, при изучении смежных предметов, в технике, экономике.

В процессе преподавания школьного курса математики перед учителем возникают две проблемы:

Взятые из жизни задачи перевести на язык математики.

Наоборот, математические задачи связать с жизнью с прак тикой.

Зачем изучать тему?

Какова связь с другими предметами? Жизнью?

Для успешного освоения курса математики необходимо ориентировать детей на изучение его теоретических основ . Формировать умения и отрабатывать навыки решения задач можно лишь, опираясь на теоретические знания учащихся.

Именно на данном этапе изучения степеней учитель должен сформировать у учащихся качественные знания, т.к. в дальнейшем учащимся эти знания понадобятся для изучения степеней с рациональным показателем, степеней с отрицательным показателем, для более сложных преобразований выражений и т.п.

Одна из главных задач преподавателя - организовать работу таким образом, чтобы к выпускному письменному экзамену ученики были способны выдвинуть самостоятельную идею при решении конкретной задачи, наметить план этого решения, грамотно обосновать свои действия, найти способы оценки и проверки получившегося ответа. Для получения подобного результата нужна серьезная теоретическая подготовка.

Опыт работы подсказывает необходимость объединять в единую систему различных форм обучения: устные опросы учащихся, мозговые штурмы, математические диктанты, письменные и устные самостоятельные работы, тестовые задания и т.д. Учитель должен в своей работе осуществлять дифференцированный и личностно-ориентированный подход к учащимся, применять И К Т, использовать на уроках элементы здоровьесберегающих технологий. Учитель должен воспитывать стремление учащихся к получению знаний, учить преодолевать трудности, формировать навыки сотрудничества, культуры общения, культуры диалога.

I I .Основная часть.

I I .1.Методическое обеспечение темы.

Методика-совокупность методов обучения чему - нибудь , практического выполнения чего-нибудь. Самым важным для учителя считается вопрос как?

-как вызвать интерес к учебе?

-как сохранить и укрепить здоровье ребенка?

-как повысить мотивацию?

-как добиться активности на уроке и одновременно обеспечить усвоение материала?

-как обеспечить успешность каждого ученика в обучении?

-как эффективно использовать в работе новые методы и новые педагогические технологии , способствующие повышению качества образования .

Учитель должен находиться в постоянном поиске путей совершенствования учебно-воспитательного процесса. На сегодняшний день есть вопрос из вопросов : как работать на уроке со всем классом и одновременно с каждым учеником ?Ответом, направленным на разрешение основного противоречия традиционной школы, связанного с групповой формой обучения и индивидуальным характером усвоения может быть принцип дифференцированного подхода к обучению, но осуществляемый на индивидуальном уровне. Задача же педагога при осуществлении данного подхода в обучении становится создание таких психолого-педагогических условий, которые обеспечивали бы активное стимулирование учащихся самооценкой образовательной деятельности на основе самообразования, саморазвития, самовыражения в ходе овладения знаниями.

Одна из важных задач образования –это создание условий для того, чтобы каждый ученик мог полностью реализовать себя, желал и умел учиться. Для успешного решения данной задачи , учитель должен использовать в своей работе разнообразные методы обучения:

1.Метод устного изложения знаний учителем и активизация познавательной активности учащихся: рассказ, объяснение, школьная лекция, метод иллюстрации демонстрации при устном изложении изучаемого материала (вербальные методы).

2.Метод закрепления изучаемого материала: тренировочные упражнения, тренинги .

3.Методы самостоятельной работы по осмыслению и усвоению нового материала

4.Методы учебной работы по применению на практике и выработке умений и навыков.

5.Метод проверки и оценки знаний, умений и навыков учащихся .

Учитель должен сделать урок не только познавательным, но и интересным, увлекательным. Для этого необходимо разнообразить типы уроков, применять современные методы обучения.

I I .2.Методические требования к теме .

Урок №1.Определение степени с натуральным показателем.

Урок№2.Определение степени с натуральным показателем.

Урок№4.Умножение и деление степеней.

Урок№5.Возведение в степень произведения.

Урок№6.Свойства степени с натуральным показателем.

Урок№7.Зачетное занятие по теме.

При изучении данной темы, учитель должен сформировать у учащихся понятие степени, основания степени, показателя степени. Определение в случаях, когда n =1 и n -натуральное число, отличное от нуля. Определение степени с нулевым показателем. Свойства степеней; должен научить производить вычисление для любых значений а и натуральных значений n .

В этой статье разберем основные свойства степеней, а также какие операции со степенями возможны в математике. А еще изучим свойства степеней с разными и одинаковыми основаниями и, конечно, потренируемся на примерах.

О чем эта статья:

7 класс, 8 класс

Что такое степень числа

В учебниках по математике можно встретить такое определение:

a — основание степени;

n — показатель степени.

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) само на себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число 2 в третью степень, то она решается довольно просто:

2 — основание степени;

3 — показатель степени.

Если вам нужно быстро возвести число в степень, можно использовать наш онлайн-калькулятор. Но чтобы не упасть в грязь лицом на контрольной по математике, придется все-таки разобраться с теорией.

Рассмотрим пример из жизни, чтобы было понятно, для чего можно использовать возведение чисел в степень на практике.

Задачка про миллион: представьте, что у вас есть миллион рублей. За один год вы заработали на нем еще два. Еще через год каждый миллион принес еще два и т. д. Получается, что миллион каждый год утраивается. Был один, а стало три — и так каждый год. Здорово, правда? А теперь посчитаем, какая сумма у вас будет через 4 года.

Как решаем: один миллион умножаем на три (1·3), затем результат умножаем на три, потом еще на три. Наверное, вам уже стало стало скучно, потому что вы поняли, что три нужно умножить само на себя четыре раза. Так и сделаем:

3·3·3·3 = 81. То есть получается, что три в степени четыре равно 81.

Математики заскучали и решили все упростить:

Ответ: через четыре года у вас будет 81 миллион.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени 2) и куб (показатель степени 3).

Читайте также: