Регрессия оценка качества модели реферат

Обновлено: 04.07.2024

Начальным пунктом эконометрического анализа зависимостей обычно является оценка линейной зависимости переменных. Это объясняется простотой исследования линейной зависимости. Поэтому проверка наличия такой зависимости, оценивание ее индикаторов и параметров является одним из важнейших направлений приложения математической статистики.

Наиболее простым для изучения является случай взаимосвязи двух переменных х и у. Если это реальные статистические данные, то мы никогда не получим простую линию – линейную, квадратичную, экспоненциальную и т.д. Всегда будут присутствовать отклонения зависимой переменной, вызванные ошибками измерения, влиянием неучтенных величин или случайных факторов. Связь переменных, на которую накладываются воздействия случайных факторов, называется статистической связью. Наличие такой связи заключается в том, что изменение одной переменной приводят к изменению математического ожидания другой переменной.

Выделяют два типа взаимосвязей между переменными х и у:

1) переменные равноправны, т.е. может быть не известно, какая из двух переменных является независимой, а какая – зависимой;

2) две исследуемые переменные не равноправны, но одна из них рассматривается как объясняющая (или независимая), а другая как объясняемая (или зависящая от первой).

В первом случае говорят о статистической взаимосвязи корреляционного типа. При этом возникают проблемы оценки связи между переменными. Например, связь показателей безработицы и инфляции в данной стране за определенный период времени. Может стоять вопрос, связаны ли между собой эти показатели, и при положительном ответе на него встает задача нахождения формы связи. Вопрос о наличии связи между экономическими переменными сводится к определению конкретной формулы (спецификации) такой связи, устойчивой к изменению числа наблюдений. Для этого используются специальные статистические методы и, соответственно, показатели, значения которых определенным образом (и с определенной вероятностью) свидетельствуют о наличии или отсутствии линейной связи между переменными.

Во втором случае, когда изменение одной из переменных служит причиной для изменения другой, должно быть оценено уравнение регрессии вида

Уравнение регрессии – это формула статистической связи между переменными. Формула статистической связи двух переменных называется парной регрессией, зависимость от нескольких переменных – множественной регрессией. Например, Дж. Кейнсом была предложена линейная формула зависимости частного потребления С от располагаемого личного дохода Y_d : С = С₀+b Y_d, где С₀ > 0 – величина автономного потребления, 1> b >0 – предельная склонность к потреблению.

Выбор формулы связи переменных называется спецификацией уравнения регрессии. В данном случае выбрана линейная формула. Далее требуется оценить значения параметров и проверить надежность оценок.

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки линейных параметров регрессий используют метод наименьших квадратов (МНК), который позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений y_i результативного признака у от теоретических ŷ_i минимальна, т.е.

В линейном случае задача сводится к решению следующей системы линейных уравнений:

Для нахождения а и в воспользуемся готовыми формулами, которые легко получаются решением системы:

a = `у - b , b = (12)

Оценку качества построенной модели даст коэффициент R 2 = r_xy 2 (R 2 = r_xy 2 индекс) детерминации, а также средняя ошибка аппроксимации:

Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии или, как говорят, мерой качества подгонки регрессионной модели к наблюдаемым значениям, характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации(0 £ R 2 £ 1), определяемый по формуле:

Заметим, что коэффициент детерминации R 2 имеет смысл рассматривать только при наличии свободного члена в уравнении регрессии, так как лишь в этом случае верны равенства:

Если известен коэффициент детерминации R 2 , то критерий значимости уравнения регрессии или самого коэффициента детерминации может быть записан в виде

В случае парной линейной модели коэффициент детерминации равен квадрату коэффициента корреляции. Тогда

Существуют 2 этапа интерпретации уравнения регрессии.

1. Первый состоит в словесном истолковании уравнения так, чтобы оно было понятно человеку, не являющемуся специалистом в области эконометрики и статистики.

2. На втором этапе необходимо решить, следует ли ограничиться первым этапом или провести более детальное исследование зависимости.

Будет проиллюстрирован моделью регрессии для функции спроса, т.е. регрессией между расходами потребителя на питание у и располагаемым личным доходом х по данным, приведенным в таблице 1 для США за период с 1959 по 1983[1]

Актуальность выбранной темы определяется тем, что в эконометрике широко используются методы статистики. Во многих практических задачах прогнозирования, изучая различного рода связи в экономических, производственных системах, необходимо на основании экспериментальных данных выразить зависимую переменную в виде некоторой математической функции от независимых переменных – регрессоров, то есть построить регрессионную модель. Регрессионный анализ позволяет:

· производить расчет регрессионных моделей путем определения значений параметров – постоянных коэффициентов при независимых переменных – регрессорах, которые часто называют факторами;

· проверить гипотезу об адекватности модели имеющимся наблюдениям;

· использовать модель для прогнозирования значений зависимой переменной при новых или ненаблюдаемых значениях независимых переменных.

Целью курсовой работы явилось исследование регрессионного анализа и применение его в эконометрике. Для достижения поставленной цели были решены следующие задачи:

· изучение основных положений регрессионного анализа

· рассмотрение оценки параметров парной регрессионной модели

· изучение интервальной оценки функции регрессии и ее параметров

· исследование оценки значимости уравнения регрессии и особенностей применения коэффициента детерминации

· рассмотрение практических задач

Предметом исследования явились математико-статистические методы в экономических исследованиях.

Объект исследования курсовой работы – практическая задача по применению регрессионного анализа в эконометрике.

Информационную базу составили труды отечественных ученых-экономистов в области эконометрических исследований, публикации, Интернет источники и личные наблюдения автора.

Для написания курсовой работы использовались методы статистической обработки информации, методы аналитических процедур и возможности математических расчетов для обоснования экономических исследований.

3. Глава 1. Теоретические и методологические основы применения регрессионного анализа в эконометрике

1.1. Основные положения регрессионного анализа

Ставя цель дать количественное описание взаимосвязи между экономическими переменными, эконометрика прежде всего связана с методами регрессии и корреляции.

Регрессия [regression] — это зависимость среднего значения какой-либо случайной величины от некоторой другой величины или нескольких величин[1] . Следовательно, при регрессионной связи одному и тому же значению x величины X (в отличие от функциональной связи) могут соответствовать разные случайные значения величины Y. Распределение этих значений называется условным распределением Y при данном X = x.

Уравнение, связывающее эти величины, называется уравнением регрессии, а соответствующий график — линией регрессии величины Y по X .

Формула для вычисления коэффициента детерминации:

y_i — выборочные данные, а f_i — соответствующие им значения модели.

Также это квадрат корреляции Пирсона между двумя переменными. Он выражает количество дисперсии, общей между двумя переменными.

Коэффициент принимает значения из интервала [0;1]. Чем ближе значение к 1 тем ближе модель к эмпирическим наблюдениям.

В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, то есть R 2 = r 2 .

Иногда показателям тесноты связи можно дать качественную оценку (шкала Чеддока) (приложение 3).

Функциональная связь возникает при значении равном 1, а отсутствие связи — 0. При значениях показателей тесноты связи меньше 0,7 величина коэффициента детерминации всегда будет ниже 50 %. Это означает, что на долю вариации факторных признаков приходится меньшая часть по сравнению с остальными неучтенными в модели факторами, влияющими на изменение результативного показателя. Построенные при таких условиях регрессионные модели имеют низкое практическое значение.

В настоящее время регрессионный анализ используется как в естественнонаучных исследованиях, так и в обществоведении.

Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой или независимых переменных известна.

Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.

Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значений зависимой переменной.

Решение задач основывается на анализе соответствующих параметров (статистических данных) в которых всегда неизбежно присутствуют отклонения, вызванные случайными ошибками. Поэтому существуют специальные методы оценки как уравнения регрессии в целом, так и отдельных ее параметров.

Глава 2. Практическое применение регрессионного анализа в эконометрике

В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) зависимость между переменными величинами у и х. Ее можно выразить аналитически с помощью формул и уравнений и графически в виде геометрического места точек в системе прямоугольных координат. Для выражения регрессии служат эмпирические и теоретические ряды, их графики — линии регрессии, а также корреляционные уравнения (уравнения регрессии) и коэффициент линейной регрессии.

Показатели регрессии выражают корреляционную связь двусторонне, учитывая изменение средней величины признака у при изменении значений x_i признака х, и, наоборот, показывают изменение средней величины признака х по измененным значениям y_i признака у.

Форма связи между показателями может быть разнообразной. И поэтому задача состоит в том, чтобы любую форму корреляционной связи выразить уравнением определенной функции (линейной, параболической и т.д.), что позволяет получать нужную информацию о корреляции между переменными величинами у и х, предвидеть возможные изменения признака у на основе известных изменений х, связанного с у корреляционно.

Построение линейной регрессии сводится к оценке ее параметров – a и b. Оценки параметров линейной регрессии могут быть найдены разными методами. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратовВ прогнозных расчетах по уравнению регрессии путем подстановки в него соответствующего значения х определяется предсказываемое значение. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ŷ_x , то есть m_ŷ _x , и соответственно интервальной оценкой прогнозного значения (у * ).После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров. Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. Библиографический список 1. Басовский Л.Е., Прогнозирование и планирование в условиях рынка, учебное пособие.- М.: ИНФРА-М, - 2002.-260с.2. Бережная Е.В., Бережной В.И., Математические методы моделирования экономических систем, учебное пособие, 2е изд.,- М.: Финансы и статистка, - 2005, 432с.3. Гладилин А.В., Эконометрика: учебное пособие. – М.:КНОРУС, 2006.–232с.4. Домбровский В.В., Эконометрика: учебник.- М.: Новый учебник, 2004.-342с.5. Елисеева И.И., Эконометрика: учебник для вузов.- М.: Финансы и статистика, 2002.-344с.6. Елисеева И.И., Эконометрика: учебник, 2е изд.- М.: Финансы и статистика, 2005.-576с.7. Елисеева И.И., Практикум по эконометрике: учебное пособие.- М.: Финансы и статистика, 2002.-192с.8. Зандер Е.В., Эконометрика: учебно-методический комплекс, - Красноярск: РИО КрасГУ, 2003.- 36с.9. Колемаев В.А. Эконометрика: учебник, - М.: ИНФРА-М, 2006. – 160с.10. Интернет: Википедия Приложение 1

Вид функции, у	Первая производная, y`_x	Коэффициент эластичности,Э= y`_x *(х/у)
ЛинейнаяУ=а+b*x+ε	b	Э=(bx)/(a+bx)
Парабола второго порядкаy=a+bx+cx 2 +ε	B+2cx	Э=((b+2cx)x)/(a+bx+c*x 2 )
Гиперболаy=a+b/x+ε	-b/x 2	Э=(-b)/(a*x+b)
Показательнаяy=ab x ε	ln bab x	Э=x*ln b
Степеннаяy=ax b ε	Abx b-1	Э=b
Полулогарифмическаяy=a+b*lnx+ε	b/x	Э=b/(a+b*ln x)
Логистическаяy=a/(1+b*e -cx +ε )	(abce -cx )/(1+be -cx ) 2	Э=(cx)/((1/b)e cx +1)
Обратнаяy=1/(a+b*x+ε)	-b/((a+b*x) 2 )	Э=(-bx)/(a+bx)

Приложение 2

∑(у-у) 2	=	∑(ŷ_х -у) 2	+	∑(у- ŷ_х ) 2
Общая сумма квадратов отклонений	=	Сумма квадратов отклонений, объясненная регрессией	+	Остаточная сумма квадратов отклонений

Приложение 3

Количественная мера тесноты связи	Качественная характеристика силы связи
0,1 - 0,3	Слабая
0,3 - 0,5	Умеренная
0,5 - 0,7	Заметная
0,7 - 0,9	Высокая
0,9 - 0,99	Весьма высокая

[1] Интернет. Экономико-математический словарь.

[2] Е.В. Зандер, Эконометрика: Учебно-методический комплекс., Красноярск: Рио КрасГУ, 2003, 15с.

[3] Е.В. Бережная, Математические методы моделирования экономических систем: учебное пособие, 2е изд., М.: Финансы и статистика, 2005, 148с

[4] И.И. Елисеева, Эконометрика: учебник для вузов., М.: Финансы и статистика, 2002 – 36с.

[5] И.И. Елисеева, Эконометрика: учебник для вузов., 2-е изд., М.: Финансы и статистика, 2005 – 81с

[6] В.А. Колемаев, Эконометрика: учебник. – М.: ИНФРА-М, 2006, 46с

[7] И.И. Елисеева, Эконометрика: учебник для вузов., М.: Финансы и статистика, 2002 – 42с.

[8] И.И. Елисеева, Эконометрика: учебник для вузов., М.: Финансы и статистика, 2002 – 62с

[9] М. Езекил: Методы анализа корреляций и регрессий., М.:Статистика, 1966.-393с

[10] Н.Дрейнер, Г.Смит: Прикладной регрессионный анализ/Пер. с англ., М.:Статистика , 1973, 140с

[11] А.В. Гладилин, Эконометрика: учебное пособие.- М.:КНОРУС, 2006.- 68

[12] В.В. Дмитровский: Эконометрика: учебник, М.: Новый учебник, 2004, 27с.

Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, что эти данные являются значениями случайной величины. Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.

Вложенные файлы: 1 файл

Основы регрессионного анализа .docx

Реферат
Основы регрессионного анализа

Содержание

ВВЕДЕНИЕ

Для решения задач экономического анализа и прогнозирования очень часто используются статистические, отчетные или наблюдаемые данные. При этом полагают, что эти данные являются значениями случайной величины. Случайной величиной называется переменная величина, которая в зависимости от случая принимает различные значения с некоторой вероятностью. Закон распределения случайной величины показывает частоту ее тех или иных значений в общей их совокупности.

При исследовании взаимосвязей между экономическими показателями на основе статистических данных часто между ними наблюдается стохастическая зависимость. Она проявляется в том, что изменение закона распределения одной случайной величины происходит под влиянием изменения другой. Взаимосвязь между величинами может быть полной (функциональной) и неполной (искаженной другими факторами).

Пример функциональной зависимости выпуск продукции и ее потребление в условиях дефицита.

Неполная зависимость наблюдается, например, между стажем рабочих и их производительностью труда. Обычно рабочие с большим стажем трудятся лучше молодых, но под влиянием дополнительных факторов образование, здоровье и т.д. эта зависимость может быть искажена.

Раздел математической статистики, посвященный изучению взаимосвязей между случайными величинами, называется корреляционным анализом (от лат. correlatio соотношение, соответствие).

Основная задача корреляционного анализа это установление характера и тесноты связи между результативными (зависимыми) и факторными (независимыми) (признаками) в данном явлении или процессе. Корреляционную связь можно обнаружить только при массовом сопоставлении фактов. Характер связи между показателями определяется по корреляционному полю. Если у зависимый признак, а х независимый, то, отметив каждый случай х (i) с координатами х и yi, получим корреляционное поле.

Теснота связи определяется с помощью коэффициента корреляции, который рассчитывается специальным образом и лежит в интервалах отминус единицы до плюс единицы.

Если значение коэффициента корреляции лежит в интервале от 1 до 0,9 по модулю, то отмечается очень сильная корреляционная зависимость. В случае если значение коэффициента корреляции лежит в интервале от 0,9 до 0,6, то говорят, что имеет место слабая корреляционная зависимость. Наконец, если значение коэффициента корреляции находится в интервале от – 0,6 до 0,6, то говорят об очень слабой корреляционной зависимости или полном ее отсутствии.

Таким образом, корреляционный анализ применяется для нахождения характера и тесноты связи между случайными величинами. Не все факторы, влияющие на экономические процессы, являются случайными величинами. Поэтому при анализе экономических явлений обычно рассматриваются связи между случайными и неслучайными величинами. Такие связи называются регрессионными, а метод математической статистики, их изучающий, называется регрессионным анализом. Рассмотрим, что представляет собой эта значимость. Обозначим коэффициент детерминации, полученный при исключении из правой части уравнения переменной. При этом мы получим уменьшение объясненной дисперсии, на величину. Для оценки значимости включения переменной используется статистика, имеющая распределение Фишера при нулевом теоретическом приросте. Вообще, если из уравнения регрессии исключаются переменных, статистикой значимости исключения будет. Пошаговая процедура построения модели. Основным критерием отбора аргументов должно быть качественное представление о факторах, влияющих на зависимую переменную, которую мы пытаемся смоделировать. Очень хорошо реализован процесс построения регрессионной модели: на машину переложена значительная доля трудностей в решении этой задачи. Возможно построение последовательное построение модели добавлением и удалением блоков переменных.

Объяснение принципов работы с регрессионным анализом начнем с более простого — парного метода.

Парный регрессионный анализ

Первые действия при использовании регрессионного анализа будут практически идентичны предпринятым нами в рамках вычисления коэффициента корреляции. Три основных условия эффективности корреляционного анализа по методу Пирсона — нормальное распределение переменных, интервальное измерение переменных, линейная связь между переменными — актуальны и для множественной регрессии. Соответственно, на первом этапе строятся диаграммы рассеяния, проводится статистически-описательный анализ переменных и вычисляется линия регрессии. Как и в рамках корреляционного анализа, линии регрессии строятся методом наименьших квадратов.

Принципиальная идея регрессионного анализа состоит в том, что, имея общую тенденцию для переменных — в виде линии регрессии, — можно предсказать значение зависимой переменной, имея значения независимой.

Разность между исходным и предсказанным значениями называется остатком (с этим термином — принципиальным для статистики — мы уже сталкивались при анализе таблиц сопряженности).

Анализ соотношения исходных и предсказанных значений служит для оценки качества полученной модели, ее прогностической способности. Одним из главных показателей регрессионной статистики является множественный коэффициент корреляции К — коэффициент корреляции между исходными и предсказанными значениями зависимой переменной. В парном регрессионном анализе он равен обычному коэффициенту корреляции Пирсона между зависимой и независимой переменной. Чтобы содержательно интерпретировать множественный В, его необходимо преобразовать в коэффициент детерминации. Это делается так же, как и в корреляционном анализе — возведением в квадрат. Коэффициент детерминации Я-квадрат (К) показывает долю вариации зависимой переменной, объясняемую независимой (независимыми) переменными.

Чем больше величина коэффициента детерминации, тем выше качество модели.

Регрессионная статистика включает в себя также дисперсионный анализ. С его помощью мы выясняем: 1) какая доля вариации (дисперсии) зависимой переменной объясняется независимой переменной; 2) какая доля дисперсии зависимой переменной приходится на остатки (необъясненная часть); 3) каково отношение этих двух величин (/А-отношение). Дисперсионная статистика особенно важна для выборочных исследований — она показывает, насколько вероятно наличие связи между независимой и зависимой переменными в генеральной совокупности. Однако и для сплошных исследований (как в нашем примере) изучение результатов дисперсионного анализа небесполезно. В этом случае проверяют, не вызвана ли выявленная статистическая закономерность стечением случайных обстоятельств, насколько она характерна для того комплекса условий, в которых находится обследуемая совокупность, т. е. устанавливается не истинность полученного результата для какой-то более обширной генеральной совокупности, а степень его закономерности, свободы от случайных воздействий.

Дополнительным условием корректности множественной регрессии (наряду с интервальностью, нормальностью и линейностью) является отсутствие мультиколлинеарности — наличия сильных корреляционных связей между независимыми переменными.

Интерпретация статистики множественной регрессии включает в себя все элементы, рассмотренные нами для случая парной регрессии. Кроме того, в статистике множественного регрессионного анализа есть и другие важные составляющие.

Работу с множественной регрессией мы проиллюстрируем на примере тестирования гипотез, объясняющих различия в уровне электоральной активности по регионам России. В ходе конкретных эмпирических исследований были высказаны предположения, что на уровень явки избирателей влияют:

Дополнительная полезная статистика в анализе соотношения исходных и предсказанных значений зависимой переменной — расстояние Махаланобиса и расстояние Кука. Первое — мера уникальности случая (показывает, насколько сочетание значений всех независимых переменных для данного случая отклоняется от среднего значения по всем независимым переменным одновременно). Второе — мера влиятельности случая. Разные наблюдения по-разному влияют на наклон линии регрессии, и с помощью расстояния Кука можно сопоставлять их по этому показателю. Это бывает полезно при чистке выбросов (выброс можно представить как чрезмерно влиятельный случай).

Регрессионный анализ своей целью имеет вывод, определение (идентификацию) уравнения регрессии, включая статистическую оценку его параметров. Уравнение регрессии позволяет найти значение зависимой переменной, если величина независимой i или независимых переменных известна. Практически, речь идет о том, чтобы, анализируя множество точек на графике (т.е. множество статистических данных), найти линию, по возможности точно отражающую заключенную в этом множестве закономерность (тренд, тенденцию), линию регрессии.

По числу факторов различают одно-, двух- и многофакторные уравнения регрессии.

По характеру связи однофакторные уравнения регрессии подразделяются на:

линейные
степенные
показательные

Линейные взаимосвязи могут быть положительными или отрицательными. Если вы обнаружили, что количество поисково-спасательных операций увеличивается при возрастании среднесуточной температуры, такое отношение является положительным; имеется положительная корреляция. Другой способ описать эту положительную взаимосвязь - сказать, что количество поисково-спасательных операций уменьшается при уменьшении среднесуточной температуры. Соответственно, если вы установили, что число преступлений уменьшается при увеличении числа полицейских патрулей, данное отношение является отрицательным. Также, можно выразить это отрицательное отношение, сказав, что количество преступлений увеличивается при уменьшении количества патрулей. На рисунке ниже показаны положительные и отрицательные отношения, а также случаи, когда две переменные не связаны отношениями:

Диаграммы рассеивания: положительная связь, отрицательная связь и пример с 2 не связанными переменными.

В данной статье мы поговорим о том, как понять, качественную ли модель мы построили. Ведь именно качественная модель даст нам качественные прогнозы.

Начнём с модели линейной регрессии. Многое из сказанного будет распространяться и на другие виды.

Модель линейной регрессии (оценка МНК)

Под моделью линейной регрессии будем понимать модель вида:

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b₀, b₁, …, b_k – коэффициенты модели.

Итак, куда смотреть?

стандартная ошибка,
t-статистика,
вероятность значимости коэффициента.

Последняя является наиболее универсальной и показывает, с какой вероятностью удаление из модели фактора, соответствующего данному коэффициенту, не окажется значимым.

Открываем панель и смотрим на последний столбец, ведь он – именно тот, кто сразу же скажет нам о значимости коэффициентов.

Факторов с большой вероятностью незначимости в модели быть не должно.

Как вы видите, при исключении последнего фактора коэффициенты модели практически не изменились.

Возможные проблемы: Что делать, если согласно вашей теоретической модели фактор с большой вероятностью незначимости обязательно должен быть? Существуют и другие способы определения значимости коэффициентов. Например, взгляните на матрицу корреляции факторов.

Коэффициент корреляции показывает силу линейной зависимости между двумя переменными. Он изменяется от -1 до 1. Близость к -1 говорит об отрицательной линейной зависимости, близость к 1 – о положительной.

Облако наблюдений позволяет визуально определить, похожа ли зависимость одной переменной от другой на линейную.

Если среди факторов встречаются сильно коррелирующие между собой, исключите один из них. При желании вместо модели обычной линейной регрессии вы можете построить модель с инструментальными переменными, включив в список инструментальных исключённые из-за корреляции факторы.

Матрица корреляции не имеет смысла для модели нелинейной регрессии, поскольку она показывает только силу линейной зависимости.

Коэффициент детерминации (R 2 ) – наиболее распространённая статистика для оценки качества модели. R 2 рассчитывается по следующей формуле:

n – число наблюдений;

y_i — значения объясняемой переменной;

— среднее значение объясняемой переменной;

ỹ_i — модельные значения, построенные по оцененным параметрам.

R 2 принимает значение от 0 до 1 и показывает долю объяснённой дисперсии объясняемого ряда. Чем ближе R 2 к 1, тем лучше модель, тем меньше доля необъяснённого.

Возможные проблемы: Проблемы с использованием R 2 заключаются в том, что его значение не уменьшается при добавлении в уравнение факторов, сколь плохи бы они ни были.

Он гарантированно будет равен 1, если мы добавим в модель столько факторов, сколько у нас наблюдений. Поэтому сравнивать модели с разным количеством факторов, используя R 2 , не имеет смысла.

где k – число факторов, включенных в модель.

Коэффициент Adj R 2 также принимает значения от 0 до 1, но никогда не будет больше, чем значение R 2 .

Аналогом t-статистики коэффициента является статистика Фишера (F-статистика). Однако если t-статистика проверяет гипотезу о незначимости одного коэффициента, то F-статистика проверяет гипотезу о том, что все факторы (кроме константы) являются незначимыми. Значение F-статистики также сравнивают с критическим, и для него мы также можем получить вероятность незначимости. Стоит понимать, что данный тест проверяет гипотезу о том, что все факторы одновременно являются незначимыми. Поэтому при наличии незначимых факторов модель в целом может быть значима.

Возможные проблемы: Большинство статистик строится для случая, когда модель включает в себя константу. Однако в Prognoz Platform мы имеем возможность убрать константу из списка оцениваемых коэффициентов. Стоит понимать, что такие манипуляции приводят к тому, что некоторые характеристики могут принимать недопустимые значения. Так, R 2 и Adj R 2 при отсутствии константы могут принимать отрицательные значения. В таком случае их уже не получится интерпретировать как долю, принимающую значение от 0 до 1.

Для моделей без константы в Prognoz Platform рассчитываются нецентрированные коэффициенты детерминации (R 2 и Adj R 2 ). Модифицированная формула приводит их значения к диапазону от 0 до 1 даже в модели без константы.

Посмотрим значения описанных критериев для приведённой выше модели:

Как мы видим, коэффициент детерминации достаточно велик, однако есть ещё значительная доля необъяснённой дисперсии. Статистика Фишера говорит о том, что выбранная нами совокупность факторов является значимой.

Кроме критериев, позволяющих говорить о качестве модели самой по себе, существует ряд характеристик, позволяющих сравнивать модели друг с другом (при условии, что мы объясняем один и тот же ряд на одном и том же периоде).

Большинство моделей регрессии сводятся к задаче минимизации суммы квадратов остатков (sum of squared residuals, SSR). Таким образом, сравнивая модели по этому показателю, можно определить, какая из моделей лучше объяснила исследуемый ряд. Такой модели будет соответствовать наименьшее значение суммы квадратов остатков.

Возможные проблемы: Стоит заметить, что с ростом числа факторов данный показатель так же, как и R 2 , будет стремиться к граничному значению (у SSR, очевидно, граничное значение 0).

Некоторые модели сводятся к максимизации логарифма функции максимального правдоподобия (LogL). Для модели линейной регрессии эти задачи приводят к одинаковому решению. На основе LogL строятся информационные критерии, часто используемые для решения задачи выбора как регрессионных моделей, так и моделей сглаживания:

информационный критерий Акаике (Akaike Information criterion, AIC)
критерий Шварца (Schwarz Criterion, SC)
критерий Ханнана-Куина (Hannan-Quinn Criterion, HQ)

Как можно увидеть, данная модель хоть и дала меньшую сумму квадратов остатков, оказалась хуже по информационным критериям и по скорректированному коэффициенту детерминации.

Модель считается качественной, если остатки модели не коррелируют между собой. В противном случае имеет место постоянное однонаправленное воздействие на объясняемую переменную не учтённых в модели факторов. Это влияет на качество оценок модели, делая их неэффективными.

Для проверки остатков на автокорреляцию первого порядка (зависимость текущего значения от предыдущих) используется статистика Дарбина-Уотсона (DW). Её значение находится в промежутке от 0 до 4. В случае отсутствия автокорреляции DW близка к 2. Близость к 0 говорит о положительной автокорреляции, к 4 — об отрицательной.

Возможные проблемы: Статистика Дарбина-Уотсона неприменима к моделям без константы, а также к моделям, которые в качестве факторов используют лагированные значения объясняемой переменной. В этих случаях статистика может показывать отсутствие автокорреляции при её наличии.

Модель линейной регрессии (метод инструментальных переменных)

Модель линейной регрессии с инструментальными переменными имеет вид:

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, x̃₁, …, x̃_k – смоделированные при помощи инструментальных переменных объясняющие ряды, z₁, …, z_l – инструментальные переменные, e, ∈_j – вектора ошибок моделей, b₀, b₁, …, b_k – коэффициенты модели, c_0j, c_1j, …, c_lj – коэффициенты моделей для объясняющих рядов.

Схема, по которой следует проверять качество модели, является схожей, только к критериям качества добавляется J-статистика – аналог F-статистики, учитывающий инструментальные переменные.

Модель бинарного выбора

Объясняемой переменной в модели бинарного выбора является величина, принимающая только два значения – 0 или 1.

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b₀, b₁, …, b_k – коэффициенты модели, F – неубывающая функция, возвращающая значения от 0 до 1.

Коэффициенты модели вычисляются методом, максимизирующим значение функции максимального правдоподобия. Для данной модели актуальными будут такие критерии качества, как:

Коэффициент детерминации МакФаддена (McFadden R 2 ) – аналог обычного R 2 ;
LR-статистика и её вероятность — аналог F-статистики;
Сравнительные критерии: LogL, AIC, SC, HQ.

Под моделью линейной регрессии будем понимать модель вида:

где y – объясняемый ряд, x₁, …, x_k – объясняющие ряды, e – вектор ошибок модели, b – вектор коэффициентов модели.

Коэффициенты модели вычисляются методом, минимизирующим значение суммы квадратов остатков. Для данной модели будут актуальны те же критерии, что и для линейной регрессии, кроме проверки матрицы корреляций. Отметим ещё, что F-статистика будет проверять, является ли значимой модель в целом по сравнению с моделью y = b₀ + e, даже если в исходной модели у функции f (x₁, …, x_k,b) нет слагаемого, соответствующего константе.

Подведём итоги и представим перечень проверяемых характеристик в виде таблицы:

Качеством модели регрессии называется адекватность построенной модели исходным (наблюдаемым) данным. Для оценки качества модели регрессии используются специальные показатели:

1) парной линейный коэффициент корреляции, который рассчитывается по формуле:

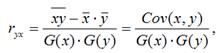
где G(x) – среднеквадратическое отклонение независимой переменной; G(y) – среднеквадратическое отклонение зависимой переменной. Также парный линейный коэффициент корреляции можно рассчитать через МНК-оценку коэффициента модели регрессии по формуле:

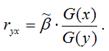
Парный линейный коэффициент корреляции характеризует степень тесноты связи между исследуемыми переменными. Он рассчитывается только для количественных переменных. Чем ближе модуль значения коэффициента корреляции к единице, тем более тесной является связь между исследуемыми переменными. Данный коэффициент изменяется в пределах . Если значение коэффициента корреляции находится в пределах от нуля до единицы, то связь между переменными прямая, т. е. с увеличением независимой переменной увеличивается и зависимая переменная, и наборот. Если коэффициент корреляции находится в пределах от минус еиницы до нуля, то связь между переменными обратная, т. е. с увеличением независимой переменной уменьшается зависимая переменная, и наоборот. Если коэффициент корреляции равен нулю, то связь между переменными отсутствует. Если коэффициент корреляции равен единице или минус единице, то связь между переменными существует функциональная связь, т. е. изменения независимой и зависимой переменных полностью соответствуют друг другу.

2) коэффициент детерминации рассчитывается как квадрат парного линейного коэффициента корреляции и обозначается как ryx2. Данный коэффициент характеризует в процентном отношении вариацию зависимой переменной, объяснённой вариацией независимой переменной, в общем объёме вариации.

Качество линейной модели множественной регрессии характеризуется с помощью показателей, построенных на основе теоремы о разложении дисперсий. Теорема. Общая дисперсия зависимой переменной может быть разложена на объяснённую и необъяснённую построенной моделью регрессии дисперсии.

В настоящее время существует две основных концепции в борьбе за повышение качества прогнозных регрессионных моделей:

− выявление с последующим исключением из анализа единственной аномальной невязки (выявление с последующим устранением нескольких аномальных невязок на основе поэтапного устранения по одному выбросу);

− нахождение с последующим исключением большего количества невязок, которые не всегда являются аномальными и их совместное отбрасывание приводит к минимальным изменениям параметров исходного регрессионного уравнения.

Первую концепцию реализуют методы Эктона, Титьена-Мура-Бекмана, а так же Прескотта-Лунда. Эти методы предназначены для выявления с последующим удалением единственного аномального измерения при нормальном законе распределения случайных величин невязок и их количестве n ≥ 30.

Вторая концепция - первый метод принципиально новой концепции − метод Кука. Несколько позднее появились методы Белсли-Ку-Уэлша и Аткинсона. Сущность метода Кука заключается в нахождении при отбрасывании уравнивающих измерений, которые стабилизируют параметры, нового регрессионного уравнения по отношению к исходному.

Поможем написать любую работу на аналогичную тему

Оценка качества регрессионной модели. Способы улучшения качества регрессионной модели.

Читайте также: