Реферат на тему параллелограмм

Обновлено: 03.07.2024

Характеристика основных свойств геометрической фигуры – параллелограмма. Анализ теоретических определений параллелограмма - если противоположные стороны попарно параллельны, если противоположные стороны попарно равны, если противоположные углы равны.

Рубрика	Математика
Вид	презентация
Язык	русский
Дата добавления	12.05.2010
Размер файла	136,3 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

HTML-версии работы пока нет.
Cкачать архив работы можно перейдя по ссылке, которая находятся ниже.

Подобные документы

Независимость событий. Условная вероятность. Независимость событий и испытаний. События А и В называются независимыми, если Р(АВ) = Р(А). Если Р(В)>0, то независимость А и В эквивалентна равенству Р(А/В) = Р(А).

реферат [20,4 K], добавлен 31.03.2003

Вычисление площади Летнего сада Петра I и площади посадок, если она составляет 4/5 от площади сада. Расчет объема Летнего дворца, если известно, что он имеет форму прямоугольного параллелепипеда. Расчет массы золота на одной занавеске во дворце.

презентация [1,3 M], добавлен 09.10.2011

Теорема Ферма, ее формулировка и доказательство в случаях, если показатель степени n - нечетное число и если n - четное число. Теорема о единственности факторизации. Дополнительные обоснования теоремы. Состав наибольшего составного числового множителя.

статья [26,6 K], добавлен 28.05.2009

Расчет площади равнобедренного и равностороннего треугольника. Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы. Расчет размеров медианы, биссектрисы.

презентация [68,7 K], добавлен 16.04.2011

Написание уравнения прямой, проходящей через определенную точку и удаленной от начала координат на заданное расстояние. Расчет длины высот параллелограмма. Построение плоскости и прямой, определение точки пересечения прямой и плоскости и угла между ними.

контрольная работа [376,1 K], добавлен 16.06.2012

Развитие вычислительных умений и навыков при решении задач. Закрепление формул для вычисления площадей геометрических фигур. Доказательства условий равенства пары треугольников. Определение соотношения прямых, заключающих равные углы у треугольников.

презентация [214,6 K], добавлен 04.12.2014

Обратная матрица. Матричные уравнения. Некоторые свойства определителей. Решение квадратной системы. Фундаментальная система решений. Метод Крамера. Если D=0 и не все Dxj=0, то система несовместна.

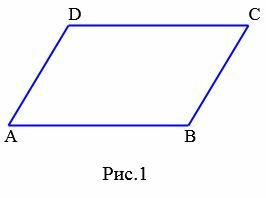
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.

На Рис.1 изображен параллелограмм поскольку \( \small AB \ || \ CD, \;\; AD \ || \ BC .\)

Свойства параллелограмма

Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).

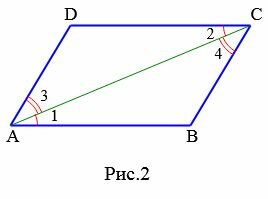Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, \( \small \angle 1=\angle 2 \), \( \small \angle 3=\angle 4 \) (см. статью Треугольники. Признаки равенства треугольников). Поэтому \( \small AB=CD, \;\; AD=BC, \;\; \angle B=\angle D. \)

Из рисунка Рис.2 имеем: \( \small \angle A=\angle 1+\angle 3, \;\; \angle C=\angle 2+\angle 4. \) Учитывая, что \( \small \angle 1=\angle 2 \) и \( \small \angle 3=\angle 4 \), получим: \( \small \angle A=\angle C. \)

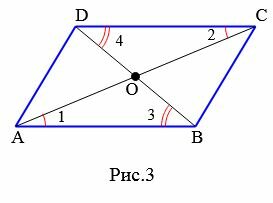
Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. \( \small \angle 1=\angle 2 \) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. \( \small \angle 3=\angle 4 \), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.

Признаки параллелограмма

Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.

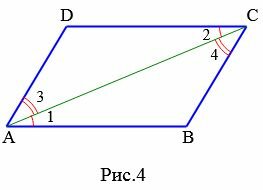Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то \( \small \angle 1=\angle 2 \) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона \( \small \angle 1=\angle 2 \). Но тогда \( \small \angle 3=\angle 4. \) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку \( \small \angle 3 \) и \( \small \angle 4 \) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм.

Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.

Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда \( \small \angle 1=\angle 2 \). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.

Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.

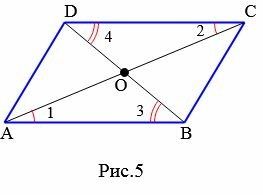Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:

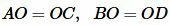Углы AOB и COD вертикальные, следовательно \( \small \angle AOB=\angle COD \). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:

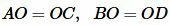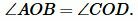Тогда AB = CD и \( \small \angle 1=\angle 2 \). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:

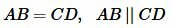и, по признаку 1 четырехугольник ABCD − параллелограмм.

Для учеников 1-11 классов и дошкольников
Бесплатные сертификаты учителям и участникам

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Параллелограмм и его свойства.pptm

Описание презентации по отдельным слайдам:

Выбранный для просмотра документ Реферат.doc

Муниципальное бюджетное общеобразовательное учреждение

Савинская средняя общеобразовательная школа

Исследовательская работа

Параллелограмм и его новые свойства

Выполнила: ученица 8Б класса

МБОУ Савинская СОШ

Кузнецова Светлана,14 лет

Руководитель: учитель математики

Тульчевская Н.А.

Ивановская область, Россия

I . Введение __________________________________________________ стр 3

II . Из истории параллелограмма ___________________________________стр 4

III Дополнительные свойства параллелограмма ______________________стр 4

IV . Доказательство свойств _____________________________________ стр 5

V . Решение задач с использованием дополнительных свойств __________стр 8

VI . Применение свойств параллелограмма в жизни ___________________стр 11

VII . Заключение _________________________________________________стр 12

VIII . Литература _________________________________________________стр 13

"Среди равных умов

при одинаковости прочих условий

превосходит тот, кто знает геометрию"

У меня возник вопрос, а есть ли у параллелограмма еще свойства, и как они помогут при решении задач.

И я решила изучить дополнительные свойства параллелограмма и показать, как их можно применить для решения задач.

Предмет исследования: параллелограмм

Объект исследования: свойства параллелограмма
Цель работы:

формулировка и доказательство дополнительных свойств параллелограмма, которые не изучаются в школе;

применение этих свойств для решения задач.

Изучить историю возникновения параллелограмма и историю развития его свойств;

Найти дополнительную литературу по исследуемому вопросу;

Изучить дополнительные свойства параллелограмма и доказать их;

Показать применение этих свойств для решения задач;

Рассмотреть применение свойств параллелограмма в жизни.
Методы исследования:

Работа с учебной и научно – популярной литературой, ресурсами сети Интернет;

Изучение теоретического материала;

Выделение круга задач, которые можно решать с использованием дополнительных свойств параллелограмма;

Наблюдение, сравнение, анализ, аналогия.

Продолжительность исследования: 3 месяца: январь-март 2016г

Из истории параллелограмма

В учебнике геометрии мы читаем следующее определение параллелограмма: параллелограмм – это такой четырехугольник, у которого противоположные стороны попарно параллельны

III Дополнительные свойства параллелограмма

В учебнике по геометрии даны только 2 свойства параллелограмма:

Противоположные углы и стороны равны

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

В различных источниках по геометрии можно встретить следующие дополнительные свойства:

Сумма соседних углов параллелограмма равна 180 0

Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;

Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;

Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;

Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;

Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.

Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.

Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.

IV Доказательство свойств параллелограмма

Сумма соседних углов параллелограмма равна 180 0

Доказательство:

А и B –внутренние односторонние углы при параллельных прямых ВС А D и секущей АВ, значит, A + B =

Дано: АBCD - параллелограмм,

АК -биссектриса А.

Доказать: АВК – равнобедренный

Доказательство:

1) 1=3 (накрест лежащие при ВС AD и секущей AK ),

2) 2=3 т. к. АК – биссектриса,

3) АВК – равнобедренный т. к. 2 угла треугольника равны

. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник

Дано: АВСD – параллелограмм,

АК – биссектриса A,

СР - биссектриса C.

Доказать: АК ║ СР

Доказательство:

1) 1=2 т. к. АК-биссектриса

2) 4=5 т.к. СР – биссектриса

3) 3=1 (накрест лежащие углы при

ВС ║ А D и АК-секущей),

4) A = C (по свойству параллелограмма), значит2=3=4=5.

4) Из п. 3 и 4 следует, что 1=4, а эти углы соответственные при прямых АК и СР и секущей ВС,

значит, АК ║ СР ( по признаку параллельности прямых)

. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых

Биссектрисы соседних углов параллелограмма пересекаются под прямым углом

Дано: АВСD - параллелограмм,

Доказать: DР АК.

Доказательство:

1) 1=2, т.к. АК - биссектриса

Пусть, 1=2=x, тогда А=2x,

2) 3=4, т.к. D Р – биссектриса

Пусть, 3=4= у, тогда D =2 y

3) A + D =180 0 , т.к. сумма соседних углов параллелограмма равна 180

2) Рассмотрим A О D

1+3=90 0 , тогда 0 (сумма углов треугольников равна 180 0 )

5. Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник

Дано: АВСD - параллелограмм, АК-биссектриса A,

CM -биссектриса C ,

BF -биссектриса B .

Доказать: KRNS -прямоугольник

Доказательство:

Исходя из предыдущего свойства 8=7=6=5=90 0 ,

значит KRNS -прямоугольник.

Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.

Дано: ABCD-параллелограмм, АС-диагональ.

Доказать: BК=DР

Доказательство: 1)DCР=КAB, как внутренние накрест лежащие при АВ ║ СD и секущей АС.

2) AКB=CDР (по стороне и двум прилежащим к ней углам АВ=С D CD Р= AB К).

А в равных треугольниках соответственные стороны равны, значит DР=BК.

Дано: ABCD-параллелограмм.

Доказать: ВКDР – параллелограмм.

Доказательство:

1) BР=КD (AD=BC, точки К и Р

делят эти стороны пополам)

2) ВР ║ КD (лежат на АD BC)

Если в четырехугольнике противоположные стороны равны и параллельны, значит, этот четырехугольник - параллелограмм.

Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.

Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.

Дано: ABCD – параллелограмм. BD и AC - диагонали.

Доказать: АС 2 +ВD 2 =2(AB 2 + AD 2 )

Доказательство: 1)АСК: AC ²= +

2) B Р D : BD 2 = B Р 2 + Р D 2 (по теореме Пифагора)

3) AC ²+ BD ²=СК²+ A К²+ B Р²+Р D ²

4) СК = ВР = Н (высота)

5) АС 2 +В D 2 = H 2 + A К 2 + H 2 +Р D 2

6) Пусть D К= A Р=х, тогда C К D : H 2 = CD 2 – х 2 по теореме Пифагора)

7) АС²+В D ² = С D 2 - х²+ АК₁²+ CD 2 -х 2 +Р D 2 ,

АС²+В D ²=2С D 2 -2х 2 + A К 2 +Р D 2

8) A К =AD+ х , Р D=AD- х ,

АС²+В D ² =2 CD 2 -2х 2 +( AD +х) 2 +( AD -х) 2 ,

АС ²+ В D²=2 С D²-2 х ² +AD 2 +2AD х + х 2 +AD 2 -2AD х + х 2 ,
АС ²+ В D²=2CD 2 +2AD 2 =2(CD 2 +AD 2 ).

V . Решение задач с использованием этих свойств

Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5 . Найдите его большую сторону.

Дано: ABCD – параллелограмм,

АК – биссектриса А,

D К – биссектриса D , АВ=5

Найти: ВС

Т.к. АК - биссектриса А, то АВК – равнобедренный.

Т.к. D К – биссектриса D , то DCK - равнобедренный

Тогда, ВС=ВК+СК=5+5 = 10

2. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.

Дано: ABCD – параллелограмм, АК – биссектриса А,

Найти: Р параллелограмма

Т.к. АК – биссектриса А, то АВК – равнобедренный.

Тогда Р=2 (14+21) =70 (см)

Дано: ABCD – параллелограмм,

D К – биссектриса D ,

Найти: Р параллелограмма

Т.к. D К – биссектриса D , то DCK - равнобедренный

Ответ: 70см или 56 см

3.Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.

1 случай: биссектрисы пересекаются вне параллелограмма

Дано: ABCD – параллелограмм, АК – биссектриса А,

D К – биссектриса D , АВ=3 см, ВС=10 см

Найти: ВМ, М N , NC

Т.к. АМ - биссектриса А, то АВМ – равнобедренный.

Т.к. DN – биссектриса D , то DCN - равнобедренный

Тогда, М N = 10 – ( BM + NC ) = 10 – (3+3)=4 см

2 случай: биссектрисы пересекаются внутри параллелограмма

Т.к. А N - биссектриса А, то АВ N – равнобедренный.

АВ=В N = 3

Т.к. DM – биссектриса D , то DCM - равнобедренный

DC = CM = 3

Тогда, BN =3 см, С N =10 – 3 = 7 см,

CM = 3 см, ВМ=10 – 3 =7 см, чего быть не может, т.к. В C =10 см

2 случай не возможен.

Ответ: 3см, 4 см, 3 см

4. (ЕГЭ-2010) В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону ВС точками М и N так, что BM : MN = 1:5. Найдите ВС, если АВ =3

В этой задаче также возможны два случая:

биссектрисы пересекаются вне параллелограмма и внутри параллелограмма.

1 случай: биссектрисы пересекаются вне параллелограмма

Дано: ABCD – параллелограмм, АМ – биссектриса А,

DN – биссектриса D , АВ=3 см, BM : MN = 1:5

Т.к. АМ - биссектриса А, то АВМ – равнобедренный.

Т.к. DN – биссектриса D , то DCN - равнобедренный

DC = CN = 3 см

Т.к. ВМ: М N =1:5, то на отрезок ВМ приходится 1 часть, а на отрезок MN – 5 частей,

Тогда, ВС= ВМ +М N + NC =3+15+3=21 см

2 случай: биссектрисы пересекаются внутри параллелограмма

Т.к. А N - биссектриса А, то АВ N – равнобедренный.

Т.к. DM – биссектриса D , то DCM - равнобедренный

Тогда, BN =3 см и BN = 6 частей, значит 1 часть = см

MN = 5 частей, значит, MN = см

Ответ: 21 см или 3,5 см

VI . Применение свойств параллелограмма в жизни

Параллелограмм не является жесткой фигурой. Эта особенность параллелограмма позволила инженерам применить свойства параллелограмма в практической жизни.

Благодаря его движимости лампу можно устанавливать в удобное для работы положение

А раздвижную решетку – отодвигать на необходимое расстояние в дверном проеме

Параллелограммный механизм — четырёхзвенный механизм, звенья которого составляют параллелограмм. Применяется для реализации поступательного движения шарнирными механизмами.

Параллелограмм с неподвижным звеном — одно звено неподвижно, противоположное совершает качательное движение, оставаясь параллельным неподвижному. Два параллелограмма, соединённых друг за другом, дают конечному звену две степени свободы, оставляя его параллельным неподвижному.

Примеры: стеклоочистители автобусов, погрузчики, штативы, подвесы, автомобильные подвески.

Параллелограмм с неподвижным шарниром — используется свойство параллелограмма сохранять постоянное соотношение расстояний между тремя точками. Пример: чертёжный пантограф — прибор для масштабирования чертежей.

Ромб — все звенья одинаковой длины, приближение (стягивание) пары противоположных шарниров приводит к раздвиганию двух других шарниров. Все звенья работают на сжатие.

Примеры — автомобильный ромбовидный домкрат, трамвайный пантограф.

Ножничный или X-образный механизм, также известный как Нюрнбергские ножницы — вариант ромба — два звена, соединённые посередине шарниром. Достоинства механизма — компактность и простота, недостаток — наличие двух пар скольжения. Два (и более) таких механизма, соединённые последовательно, образуют в середине ромб(ы). Применяется в подъёмниках, детских игрушках.

VII Заключение

Кто с детских лет занимается математикой,

тот развивает внимание, тренирует свой мозг,

свою волю, воспитывает в себе настойчивость

и упорство в достижении цели

А. Маркушевич

В ходе работы я доказала дополнительные свойства параллелограмма.

Я убедилась, что применяя эти свойства, можно решать задачи быстрее.

Я показала, как применяются эти свойства на примерах решения конкретных задач.

Я узнала много нового о параллелограмме, чего нет в нашем учебнике геометрии

Я убедилась в том, что знания геометрии очень важны в жизни на примерах применения свойств параллелограмма.

Цель моей исследовательской работы выполнена.

О том, насколько важны математические знания, говорит тот факт, что была учреждена премия тому, кто издаст книгу о человеке, который всю жизнь прожил без помощи математики. Эту премию до сих пор не получил ни один человек.

В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – параллелограмма.

Определение параллелограмма
Свойства параллелограмма
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Свойство 6
- Свойство 7
- Свойство 8
- Свойство 9
- Свойство 10: тождество параллелограмма
Определение параллелограмма

Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.

Обычно параллелограмм записывается путем перечисления четырех его вершин, например, ABCD. А пары параллельных сторон, чаще всего, обозначаются маленькими латинскими буквами, в нашем случае – a и b.

Частные случаи параллелограмма: квадрат, ромб и прямоугольник.

Свойства параллелограмма

Свойство 1

Противолежащие (или противоположные) стороны параллелограмма равны.

Свойство 2

Противолежащие углы параллелограмма равны.

Свойство 3

Сумма углов параллелограмма, прилежащих к одной стороне, равняется 180°.

Для рисунка выше: α + β = 180°.

Свойство 4

Любая из двух диагоналей параллелограмма делит его на два равных треугольника.

Свойство 5

Диагонали параллелограмма в точке пересечения делятся пополам.

Свойство 6

Точка пересечения диагоналей параллелограмма (также называется центром симметрии) одновременно является точкой пересечения его средних линий.

Средняя линия четырехугольника – это отрезок, который соединяет середины его противоположных сторон.

В данном случае средние лини – это отрезки FM и EN.

Свойство 7

Угол между двумя высотами в параллелограмме равен его острому углу.
- BL – высота, проведенная к стороне CD
- BK – высота, проеденная к стороне AD
- ∠KBL = ∠BAK
Свойство 8

Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны (т.е. расположены под углом 90° друг к другу).

Свойство 9

Биссектрисы двух противолежащих углов параллелограмма параллельны.

Углы ABC и ADC противолежащие. Их биссектрисы параллельны, т.е. BR || DP.

Свойство 10: тождество параллелограмма

Сумма квадратов диагоналей параллелограмма равняется удвоенной сумме квадратов его смежных сторон.

Признаки параллелограмма

Четырехугольник ABCD без самопересечений является параллелограммом, если для него справедливо одно из утверждений ниже:

Читайте также: