Растяжение с изгибом реферат
Обновлено: 05.07.2024
Сочетание изгиба и растяжения (сжатия) имеет место в случае:
- продольно-поперечного изгиба стержня;
- внецентренного растяжения (сжатия).
10.3.1. Изгиб с растяжением (сжатием)
Большинство элементов рамного каркаса промышленного здания одновременно работают на сжатие (растяжение) в сочетании с поперечным изгибом. Примером могут служить колонны промышленных зданий, испытывающие продольное сжатие от действия вышележащих конструкций покрытия, и поперечный изгиб от действия горизонтальных нагрузок (ветровая нагрузка, торможение крановой тележки и т.д.).
В случае действия изгиба с растяжением-сжатием (нагрузки приложены в различных плоскостях, пересекающих ось элемента, и приведены к проекциям на плоскости xoz и yoz) и растяжения (сжатия), действующей вдоль оси элемента и приложенной в центре тяжести его сечения, вызывает внутренние усилия N, Qx, Qy, Mx, My.
Исходя из принципа независимости действия сил нормальные напряжения в произвольной точке сечения с координатами х и у (см. рис. 10.5) определятся как
Учитывая, что σz(N), σz(Mx) и σz(My) ориентированы параллельно оси z, и это можно упрощенно трактовать, как линейное напряженное состояние, условие прочности может быть записано как
10.3.2. Внецентренное растяжение (сжатие)
Примером внецентренно сжатых элементов могут служить колонны, нагрузка на которые от вышележащих элементов (балок, плит) осуществляется с эксцентриситетом. На важность учета этого фактора при проектировании и монтаже указывает то, что в строительных нормах и правилах предельно допустимые величины отклонений опорных ребер от проектного положения жестко регламентируются. Однако внецентренное сжатие (растяжение) испытывают не только стойки (колонны), но и различные элементы стержневых конструкций, например, пояса стропильных ферм, если элементы решетки не удается точно сцентрировать в узел фермы (то есть добиться того, чтобы оси элементов пояса и решетки пересекались в одной точке).
Внецентренное растяжение (сжатие) возникает в том случае, когда растягивающая (сжимающая) сила, приложенная к стержню, направлена параллельно его продольной оси, но с эксцентриситетом относительно центра тяжести его поперечного сечения (рис. 10.6).
При этом под эксцентриситетом приложения нагрузки будем понимать наименьшие расстояния (xp , yp) от точки, через которую проходит линия действия внешней нагрузки Р, до главных осей инерции сечения y и х соответственно.
Путем параллельного переноса силы Р в центр тяжести сечения как в абсолютно твердом теле и замены ее внецентренного приложения учетом соответствующих изгибающих моментов Mx = P · yp и My = P · xp получаем эквивалентное напряженное состояние, которое описывается уже известной нам формулой (10.10), позволяющей определить нормальные напряжения σz=σz(N)+σz(Mx)+σz(My) в произвольной точке поперечного сечения К с координатами хК и уК.
- формула для определения нормальных напряжений при внецентренном сжатии (растяжении)
где (ix , iy - радиусы инерции сечения стержня относительно главных центральных осей х и у).
Положение нейтральной линии, необходимое при решении практических задач конструирования, связанных с разграничением растянутой и сжатой зоны сечения и определением точек, в которых действуют максимальные нормальные напряжения, определим, приравняв выражение (10.12) нулю. Учитывая, что (P / F) ≠ 0, получим
- уравнение нейтральной линии (10.13)
где x н , y н - координаты произвольной точки, лежащей на нейтральной линии
Решая полученное уравнение (10.13) в отрезках по осям координат, определим (рис.10.7).
при x н = 0: при y н = 0: (10.14)
Анализируя рис. 10.7 и формулы (10.12)…(10.14) можно сделать следующие важные практические выводы:
- Нейтральная линия пересекает координатные оси в точках квадранта, противоположному квадранту с точкой приложения силы Р.
- Максимальные значения напряжений возникают в наиболее удаленных от нейтральной линии точках (для рассматриваемого примера – B (σmin), D (σmax).
- При относительно малых значениях эксцентриситетов приложения силы Р значения хн и ун могут достигать больших величин, нейтральная линия находиться за пределами сечения и в этом случае в сечении возникают однозначные напряжения.
10.3.3. Ядро сечения
Рассмотрим более подробно последний пункт выводов и попытаемся определить условия внецентренного приложения силы P, при которых в сечении будут однозначные напряжения. Это важно при проектировании элементов, которые изготавливаются из материалов, плохо воспринимающих растяжение (например, бетон либо кирпичная кладка).
В этом случае в формулах (10.14) известными величинами становятся координаты точек, принадлежащих отрезкам х и у, определяющих положение нейтральной линии. Рассмотрим некоторые характерные особенности поведения нейтральной линии, вытекающие из анализа формул (10.14) (рис. 10.8):
- если точка приложения силы Р будет находиться на оси х или у, то нейтральная ось будет занимать положение параллельное оси у или х соответственно (рис. 10.8.а).Положению силы в точке 1 будет соответствовать нулевая лини– I, точке 2 – II, точке 3 – III, точке 4 - IV);
- при перемещении точки приложения силы Р по прямой, проходящей через центр тяжести сечения, нейтральная линия будет перемещаться параллельно самой себе (рис. 10.8. а: 5 – V, 6 – VI), так как
- из этого следует, что тангенс угла наклона нейтральной линии зависит не от численного значения координат точки приложения силы Р, а от их соотношения;
- при перемещении точки приложения силы Р по прямой, не проходящей через центр тяжести сечения, нейтральная линия будет поворачиваться вокруг некоторой точки С. Эта происходит в силу того, что точка принадлежит одновременно 2-м нулевым линиям I-I и II-II и условно может быть представлена как результат одновременного действия 2-х сил, приложенных в точках 1 и 2. В то же время и произвольно взятая точка 3, лежащая на прямой 1-2, также может быть представлена, как равнодействующая 2-х аналогичных сил, но приложенных в точках 3у и 3х (рис.10.8б).
Рассмотреть случай, когда нейтральная линия I-I будет касательной к контуру сечения (рис. 10.9). Такое ее положение будет определять условие однозначности напряжений. Тогда, используя соотношения (10.14), определяющие положение нейтральной линии, найдем значения координат точки 1 приложения силы Р, вызывающее указанное положение нейтральной линии
при x н = 0: при y н = 0: (10.15)
Точно так же можно определить положение точек 2 и 3, которые определяют положение касательных II-II и III-III. Аналогичным образом, последовательно обходя контур поперечного сечения и проводя множество касательных, соответствующими точками приложения сил можно сформировать кривую, ограничивающую определенную зону. Сформированная таким образом область, расположенная вокруг центра тяжести сечения, внутри или на контуре которой приложение силы Р, вызывает во всем поперечном сечении напряжения одного знака, называется ядром сечения.
Рассмотрим несколько примеров построения ядра сечения.
Пример 10.2. Прямоугольное сечение с размерами сторон (рис. 10.10а).
Положим, что нейтральная линия последовательно занимает положения, совпадающие со сторонами АВ, ВС, CD, DA . Найдем для каждого положения нейтральной линии соответствующее положение силы Р.
Например, касательная к сечению проходит через сторону АВ. Тогда положение точки 1 определится
Пример 10.3. Двутавровое сечение (рис. 10.10.б).
Выписываем из сортамента прокатных профилей значения квадратов радиусов инерции соответствующих рассматриваемому двутавру. Так же как и в предыдущем случае, последовательно обходя контур, рассмотрим четыре положение касательных I-I…IV-IV. Учитывая симметричность исследуемого сечения, достаточно рассмотрения положения касательных I-I и II-II. Следует указать в качестве общего замечания, что наличие внутренних углов в сечении (таких как точки соединения стенки с поясами) не вызывает появления дополнительных вершин ядра сечения, поскольку для таких точек невозможно провести касательную к сечению. Тогда для точек, лежащих на оси y, координата определится, как
а для точек, лежащих на оси х
Пример 10.4. Круглое сечение диаметром (рис. 10.10.в).
Вследствие полярной симметричности рассматриваемого сечения (т.е. симметричности относительно центра тяжести сечения), для построения ядра сечения достаточно задаться одним положением нейтральной линии:
© 2014-2022 — Студопедия.Нет — Информационный студенческий ресурс. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав (0.007)
Cложное сопротивление – такие виды нагружения бруса, при которых в поперечных сечениях возникают одновременно не менее двух внутренних силовых факторов.
Случаи сложного сопротивления условно разделяют на два вида. Первый вид составляют случаи сложного сопротивления, при которых в опасных точках бруса напряженное состояние является одноосным. В эту группу объединяют: изгиб с растяжением, косой изгиб, внецентренное растяжение-сжатие и др.

Рис. 41. Изгиб с растяжением
Условие прочности при изгибе с растяжением, пренебрегая действием поперечных сил, имеет вид:

(32)
Ко второй группе относятся такие случаи сложного сопротивления, когда напряженное состояние является плоским. Например, изгиб с кручением, растяжение(сжатие) с кручением и т.д. Для случая нагружения, относящегося к первой группе, в отличие от второй группы, нет необходимости в применении гипотез прочности.
Косой изгиб проявляется, если прикладываем к балке вертикальную нагрузку, и она при этом изгибается не только в вертикальной плоскости, но и вбок. Косой изгиб – это изгиб, при котором изогнутая ось стержня не лежит в силовой плоскости. Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).
Рассмотрим консольную балку прямоугольного сечения длиной l, нагруженную вертикальной силой P. Главная центральная ось балки (ось симметрии) y составляет некоторый малый угол α с направлением действия нагрузки.

Рис. 42. Косой изгиб
Разложим силу P на составляющие: Py = cos α, Px = sin α . Используя принцип независимости действия сил Py, рассмотрим отдельно действие каждой составляющей. Нагрузки Py и Px вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты:
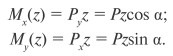
Оба изгибающих момента будут наибольшими в жесткой заделке:
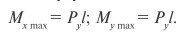
Формула суммарных нормальных напряжений при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y:

(33)
где – главные моменты инерции; h – высота, а b – ширина прямоугольного поперечного сечения балки. Величины изгибающих моментов и координат данной точки подставляются в формулу нормальных напряжений при косом изгибе, знак каждого из слагаемых определяется по физическому смыслу.
Наибольшие нормальные напряжения при косом изгибе возникнут в поперечном сечении, расположенном в жесткой заделке, в наиболее удаленных от соответствующих нейтральных осей точках 1 и 2: y = h/2, x = b/2. В точке 1 напряжения будут растягивающими:

а в точке 2 – такими же по величине, но сжимающими.
В формулах максимальных нормальных напряжений при косом изгибе – осевые моменты сопротивления балки относительно главных центральных осей инерции.
Нейтральная линия – это геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю.

Из определения нейтральной линии легко находится положение нейтральной линии, приравнивая правую часть выражения к нулю:


При косом изгибе условие прочности имеет вид:

(34)
Косой изгиб опасен тем, что при производственном браке (перекосе) могут существенно увеличиться нормальные напряжения в балке.









Изгиб с растяжением – частный случай сложного сопротивления, при котором на брус действуют продольные и поперечные нагрузки, пересекающие ось бруса. В общем случае в поперечных сечениях возникают пять внутренних усилий: действующие в двух плоскостях изгибающие моменты Mz, My, поперечные силы Qz, Qy, а также продольная сила N. Возникает сложный изгиб с растяжением или сжатием. Пренебрегая касательными напряжениями от поперечных сил Qz, Qy (для длинных балок с отношением ℓ/h > 10 их влияние незначительно), можно считать напряженное состояние в опасных точках линейным. Внецентренное растяжение или сжатие Внецентренное растяжение – частный случай изгиба с растяжением, при котором брус растягивается силами, параллельными оси бруса так, что их равнодействующая не совпадает с осью бруса, а проходит через точку Р, называемую полюсом силы. Внутренние усилия и напряжения В произвольном сечении х бруса (рис.8.7, а) методом сечений определяем внутренние усилия Рис. 8.6. Примеры деталей и узлов, работающих при внецентренном нагружении: а – болт-костыль; б – пружина сцепления; в – сварное соединение Отличны от нуля три внутренних усилия (рис. 8.7, б), от которых возникают нормальные напряжения, действующие по одной из трех пар граней (рис. 8.7, в); две другие пары граней свободны от напряжений. Имеет место линейное напряженное состояние. Напряжения в произвольной точке являются суммой трех слагаемых Учитывая, что отношение i = – радиус инерции сечения, получим О правиле знаков внутренних усилий. Формула (8.10) выведена для случая положительной растягивающей силы N и изгибающих моментов Mz, My, вызывающих растягивающие напряжения в точке, принадлежащей первой четверти осей координат (где x > 0 и y > 0). Поэтому оси координат поперечного сечения бруса следует направлять так, чтобы полюс P (точка приложения силы) находился в первом квадранте. Если сила, приложенная к брусу, сжимающая, то ее числовое значение будет со знаком минус. Анализ формулы (8.10) 1. Отсутствие координаты х свидетельствует о неизменности напряжений вдоль оси бруса. 2. В случае приложения силы в центр тяжести сечения (zP = 0, yP = 0) напряжения в любой точке сечения постоянны и равны σ = F/A, то есть центральное растяжение является частным случаем внецентренного. Рис. 8.7. Схема к определению внутренних усилий и напряжений при внецентренном приложении силы 3. Независимо от значений координат полюса Р напряжение в центре тяжести сечения (yцт =0, zцт = 0), σцт = F/A. 4. Переменные z и y в первой степени, следовательно, формула (8.10) является уравнением прямой и нормальные напряжения распределяются по линейному закону, значит должна быть нейтральная линия, на которой напряжения равны нулю. Уравнение нейтральной линии при внецентренном растяжении Нейтральная линия (нейтральная ось) – геометрическое место точек, в которых нормальное напряжение в поперечном сечении равно нулю. Приравняем нулю уравнение (8.10). Поскольку F/A ≠ 0, то выражение в скобках равно нулю Переменные z, y в первой степени, следовательно, нормальные напряжения в сечении распределяются по линейной зависимости. Полученное выражение приведем к виду уравнения прямой в отрезках, где a и b – отрезки, отсекаемые линией на осях координат. В нашем случае уравнение нейтральной линии будет записано как Свободный член полученного уравнения не равен нулю, следовательно, нейтральная линия через начало координат не проходит. Отрезки, отсекаемые нейтральной линией на осях y и z, соответственно равны: По найденным значениям отрезков проводят нейтральную линию и находят точки В и С, наиболее удаленные от нее (рис. 8.9). Выполняют это простым геометрическим построением, проводя касательные к сечению, параллельные нейтральной оси. Найденные точки – опасные, поскольку напряжения в них наибольшие по величине. Рис. 8.8. Уравнение прямой в отрезках и график прямой линии, известные из школьного курса Уравнения (8.12), связывающие координаты полюса Р – точки приложения внешней нагрузки с положением нейтральной линии, являются гиперболической функцией. Чем ближе полюс Р к центру тяжести сечения (значения yP, zP уменьшаются), тем нейтральная линия проходит дальше и в пределе стремится к бесконечности. И, наоборот, по мере отдаления точки приложения силы от центра тяжести нейтральная линия асимптотически приближается к нему. Однако пересечь центр тяжести сечения нейтральная линия не может (см. анализ формулы (8.10)). В центре тяжести σцт = F/A (рис. 8.9), поскольку yцт = 0 и zцт = 0 (подставьте в (8.10)). Нейтральная линия может разделять поперечное сечение на области, в которых действуют напряжения разных знаков. Некоторые материалы (чугун, силумин, керамика, кирпичная кладка…) хорошо сопротивляются сжатию и плохо – растяжению. Поэтому необходимо уметь определять такую область приложения нагрузки, в которой не возникают напряжения разных знаков. Ядро сечения Ядро сечения – область вокруг центра тяжести сечения, при приложении нагрузки внутри которой, напряжения во всем сечении будут одного знака. Контур ядра сечения строят путем окатывания нейтральной линией контура поперечного сечения, то есть решают задачу обратную той, в которой определяли положение нейтральной линии: куда следует прикладывать силу, чтобы нейтральная линия не пересекала контур сечения, а только касалась его. Задают несколько положений нейтральной линии, касательной к сечению (например, н.л.1, н.л.2, н.л.3), определяют координаты точек пересечения этих линий с осями координат (например, zн.л.1, yн.л.1). Затем, преобразуя уравнение (11), находят Рис. 8.10. Определение координат отрезков нейтральной линии для построения ядра сечения Рис. 8.9. Эпюра напряжений в поперечном сечении Нейтральная линия соответствующие им координаты точек ядра сечения (точки 1, 2, 3): Так как при переходе нейтральной линии с одной стороны на другую (например, от н.л 3 к н.л 4) она поворачивается вокруг угловой точки сечения, то точка приложения силы перемещается по прямой (на рис. 8.10 отрезок 3 – 4), образуя контур ядра. Пример 8.4. Построить ядро сечения для круга диаметром d. Решение. Квадрат радиуса инерции круга: Задаем положение нейтральной линии 1–1, касательной к окружности. Ее координаты: Координаты точки ядра сечения: Из симметрии сечения относительно его центра тяжести следует, что при других положениях нейтральной линии на окружности диаметром d точки ядра сечения образуют концентрический с ней круг диаметром d/4. Пример 8.5. Построить ядро сечения для прямоугольника с размером сторон bЧh. Решение. Квадраты радиусов инерции: Задаем положение нейтральной линии 1-1, касательной к верхней грани прямоугольника. Ее ко- ординаты: zн.л 1 = ∞; yн.л1 = h/2. Координаты соответствующей точки ядра сечения: Аналогично для нейтральной линии 2-2: zн.л 2 = b/2; yн.л 2 = ∞. Учитывая симметрию прямоугольного сечения относительно осей z и y, задаем положения нейтральных линий на противоположных сторонах прямоугольника и получаем еще две точки. Соединяя все точки, получаем ядро сечения в виде ромба с диагоналями, равными h/3 и b/3. Пример 8.6. Построить ядро сечения для швеллера № 20. Решение. Из таблицы сортамента выпишем исходные данные и выполним рисунок швеллера. Последовательно задаем положение нейтральной линии (I-I, II-II, III-III, IV-IV), касающейся контура сечения, и вычисляем координаты точек ядра сечения. Расчеты представлены в табличном виде. Ядро сечения имеет вид четырехугольника, асимметричного относительно оси ординат. Положение ядра сечения зависит лишь от формы и размеров поперечного сечения, но не зависит от величины приложенной силы. Расчет на прочность при внецентренном нагружении Поверочный расчет выполняют, используя условие прочности Проектный расчет обладает особенностью, связанной с тем, что геометрические характеристики, входящие в условие прочности содержат искомый размер поперечного сечения в разной степени. Площадь А измеряется в м2, а моменты сопротивления W в м3. Попытка выразить искомый yн.л. = h/2 = 20/2 = 10 см; zн.л. = ∞; размер из условия прочности приводит к трансцендентной функции, то есть аналитической функции, не являющейся алгебраической. Проектный расчет выполняют методом итераций 1 [от лат. iteratio – повторение]. В первом приближении, пренебрегая одним из внутренних усилий, – продольной силой N – подбирают размер сечения только из условия прочности при изгибе. Полученный размер подставляют в исходное уравнение и выполняют следующую пробу. Процесс повторяют до тех пор, пока невязка – разность размеров последующей и предыдущей проб, не достигнет заданной наперед малости. Пример 8.7. (Винокуров А. И. Сборник задач … 5.35). Подобрать диаметр стержня выпускного клапана. При расчете использовать усилие F в момент открывания клапана в конце рабочего хода поршня. Решение. Сила давления газов на тарелку клапана 533441Н Внутренние усилия в сечении 1-1 стержня клапана (по модулю): N = F; M = F•e. Условие прочности: По обе стороны от знака неравенства искомый диаметр – имеем трансцендентное уравнение, которое решаем методом приближений: Метод последовательных приближений, при котором каждое новое приближение вычисляют исходя из предыдущего; начальное приближение выбирается в достаточной степени произвольно. Дано: p = 1,5 МПа; e = 12 мм; D = 35 мм; [σ] = 210 МПа Разность между последним и предпоследним приближениями Процесс подбора прекращаем, принимаем d = 10 мм. Проверка: Напряжения изгиба больше напряжений растяжения в 6,9 раза Пример 8.8. (Винокуров А. И. Сборник задач … 5.38.). Из расчета на прочность определить размер h скобы струбцины. Решение. Условие прочности при внецентренном растяжении плоской фигуры σ=+≤[σ] где A = b•h; W = b•h2/6; M = F(a+h/2). Условие прочности: Требуемый размер скобы: Размер h в обеих части неравенства. Полученное уравнение – трансцендентное. Решаем его методом последовательных приближений. В первом приближении принимаем h в скобках под корнем равным нулю: h0 = 0. Тогда Невязка подбора 100 25,4 % Следующее приближение 101,58 мм. Невязка подбора 100 4,5 % Следующее приближение 102,54 мм. Невязка подбора 100 0,95 % невязка менее 1 %, поэтому выходим из цикла подбора. Принимаем h = 103 мм. Проверка: Сопоставим вклады от изгиба и растяжения в общее напряжение: Напряжения от изгиба в 8,24 раза превышают напряжения от растяжения. Полученное соотношение можно сделать более благоприятным снизив долю растягивающих напряжений от изгиба за счет уменьшения плеча е изгибающего момента. На практике применяют тавровое и двутавровое сечения, смещая центр тяжести с ближе к линии действия силы и располагая больше материала в области растягивающих напряжений, к которым хрупкие материалы более чувствительны. Рис. 8.11. Примеры выполнения поперечного сечения бруса, подверженного действию внецентренного растяжения
Деформация – изменение формы, размеров тела под действием приложенных к нему сил.
Линейная деформация – изменение линейных размеров тела, его рёбер. Линейные размеры тела могут изменяться одновременно в одном, двух или трёх взаимно перпендикулярных направлениях, что соответствует линейной, плоской и объёмной деформации. Линейная деформация, как правило, сопровождается изменением объёма тела.
Угловая деформация – изменение угловых размеров тела, углов наклона его граней. В результате угловой деформации происходит взаимное смещение граней. При этом изменяется только форма тела, объём сохраняется неизменным.
Линейная деформация связана преимущественно с действием нормальных напряжения, угловая – с действием касательных напряжений. [1]
Растяжение (сжатие) – деформация, возникающая под действием в поперечном сечении только продольной (растягивающей или сжимающей) силы.
Напряжение вдоль оси прямо пропорционально растягивающей (сжимающей) силе и обратно пропорционально площади поперечного сечения. При упругой деформации соотношение между напряжением и относительной деформацией определяется законом Гука, при этом поперечные относительные деформации выводятся из продольных путём умножения их на коэффициент Пуассона. Пластическая деформация, предшествующая разрушению части материала, описывается нелинейными законами (рисунок 1). [2]
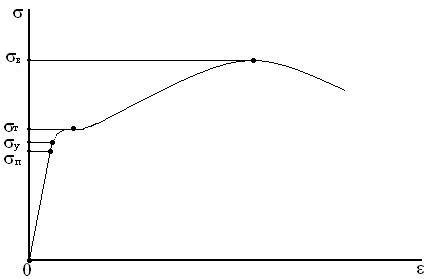
Рисунок 1 — Диаграмма растяжения
Сдвиг – деформация, характеризующаяся взаимным смещением параллельных слоёв материала под действием сил, приложенных касательно к его поверхности, при неизменном расстоянии между слоями (рисунок 2).
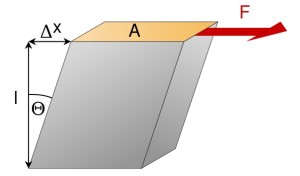
Рисунок 2 — Сдвиг
Кручение – деформация, характеризующаяся взаимным поворотом поперечных сечений тела под действием пары сил (момента) в этих сечениях (рисунок 3).
Рисунок 3 — Кручение
Изгиб – деформация, при которой происходит изменение кривизны осей тела под действием изгибающих моментов в поперечных сечениях (рисунок 4).
Читайте также:

