Радианная мера угла реферат
Обновлено: 02.07.2024
Градусная и радианная мера угла. Функция как соотношение между двумя числовыми множествами, размерность числового множества. Понятие множества значений некоторого угла. Элементарные тригонометрические функции произвольного угла: синус, косинус, тангенс.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 19.08.2009 |
| Размер файла | 239,9 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Дисциплина: "Высшая математика"
1. Градусная и радианная мера угла
Как было показано ранее, функция задает определенное соотношение между двумя числовыми множествами. Однако в некоторых случаях область определения функции может являться множеством чисел, имеющих размерность. В частности, речь идет о множестве значений некоторого угла. Прежде чем приступить к рассмотрению подобных функций, напомним некоторые факты, связанные с измерением углов.
Определение 1. Углом в называется центральный угол, опирающийся на дугу окружности, имеющей длину, равную ее части.
Исторически сложилось деление градуса на 60 минут, а минуты на 60 секунд, то есть: , . Секунды делятся на десятые, сотые и т.д. части. Градус является наиболее распространенной единицей измерения углов.
Определение 2. Углом в 1 радиан называется центральный угол, опирающийся на дугу окружности, имеющую длину, равную ее радиусу.
Таким образом, для отыскания радианной меры центрального угла достаточно длину дуги (l), на которую он опирается, разделить на длину радиуса (R), то есть .
Из сказанного выше следует, что полной окружности будет соответствовать в градусах угол в 360 раз больший, то есть . В радианах это будет радиан. Необходимо также отметить, что величина угла в градусной и радианной мере никак не связана с радиусом окружности. Следовательно, в дальнейшем можно рассматривать окружность любого радиуса, проще всего - единичного.
Формулы перехода от градусной меры дуг и углов к радианной и наоборот имеют вид:
Отсюда следует, что
1 рад = , а рад0,01745 рад.
Рассмотрим теперь координатную плоскость с началом координат в точке О. Проведем окружность единичного радиуса с центром в точке О и отметим точки ее пересечения с осями координат.
Рассмотрим произвольную точку M на окружности и вектор , который называется радиус-вектором точки M.
Будем рассматривать центральные углы AOM, образованные векторами и при перемещении точки M по окружности.
Если точка M совпадает с точкой A, то полагают равным нулю. Будем считать положительным, если вращение вектора от начального положения происходит в направлении противоположном движению часовой стрелки. В противном случае будем считать отрицательным.
Так как полный оборот вектора приводит его в то же положение, однозначно определить величину угла, если это не оговорено, нельзя. Иначе говоря, в общем случае
2. Элементарные тригонометрические функции произвольного угла
Введем определение основных тригонометрических функций угла. Для этого изобразим вначале единичную окружность.
Определение 1. Синусом угла называется отношение ординаты конца подвижного радиус-вектора , который образует угол с осью абсцисс, к длине этого радиус-вектора и обозначается .
Определение 2. Косинусом угла называется отношение абсциссы конца подвижного радиус-вектора , который образует угол с осью абсцисс, к длине этого радиус-вектора и обозначается .
Определение 3. Тангенсом угла называется отношение ординаты конца подвижного радиус-вектора , который образует угол с осью абсцисс, к абсциссе конца этого радиус-вектора и обозначается .
Определение 4. Котангенсом угла называется отношение абсциссы конца подвижного радиус-вектора , который образует угол с осью абсцисс, к ординате конца этого радиус-вектора и обозначается .
Из приведенных определений следует, что
причем у единичной окружности
Введение произвольных по знаку и абсолютной величине углов позволяет каждому действительному числу поставить в соответствие угол в радиан и, наоборот, каждому углу - однозначно определяемое действительное число, равное числу радиан. Такое взаимнооднозначное соответствие позволяет определить тригонометрические функции числового аргумента.
Определение 5. Тригонометрическая функция числа это та же тригонометрическая функция угла величиной в радиан.
Рассмотрим графики основных элементарных тригонометрических функций.
Здесь
период ; ; корни , где .
Здесь
период ; ; корни , где .
Здесь
где ; ; период ; ; корни , где .
Здесь
где ; ; период ; ; корни , где .
Здесь
; ; ; корень .
Здесь
; ; ; корень .
Здесь
; ; ; корень .
Здесь
; ; ; корней нет.
Литература
Ефимов Н.В. Высшая геометрия. Изд-во: ФИЗМАТЛИТ®, 2003. - 584c.
Клейн Ф., Феликс Христиан Клейн Высшая геометрия: Пер. с нем. Изд.3. Изд-во: ЛИБРОКОМ, 2009. - 400c.
Крищенко Александр, Канатников Анатолий Аналитическая геометрия: Учебное пособие для студентов высших учебных заведений. Издательство "Академия/Academia", 2009. - 2008c.
Фролов С. Начертательная геометрия Учебник.3-е изд., перераб. и доп. Изд-во: ИНФРА-М, ИЗДАТЕЛЬСКИЙ ДОМ, 2007. - 286c.
Подобные документы
Обозначение основных тригонометрических терминов: радианная и градусная мера угла, синус, косинус, тангенс, котангенс. Область определения функций и построение их графиков. Выведение формул сложения, суммы, разности и двойного аргумента функций.
презентация [229,3 K], добавлен 13.12.2011
Задача о делении угла на три равные части (трисекция угла), история ее происхождения. Построение трисектрисы угла (лучей, делящих угол) с помощью циркуля и линейки. Общее доказательство о трисекции угла, зависимость между ней и антипараллелограммом.
реферат [1,2 M], добавлен 12.12.2009
Перевод мер угла в градусной системе. Соотношения между градусной и часовой системами счисления. Перевод меры угла из классического вида в секунды, в десятичный и наоборот. Алгоритм (правила) и методы его перевода. Перевод мер угла в часовой системе.
контрольная работа [50,1 K], добавлен 13.05.2009
Квадратичная функция. Графиком квадратичной функции является парабола. Логарифмическая функция. Синус, косинус, тангенс, котангенс угла. Арифметическая прогрессия. Геометрическая прогрессия. Сумма бесконечной геометрической прогрессии.
контрольная работа [166,3 K], добавлен 19.05.2006
Особенности применения теорем Пифагора и косинусов в делении углов на равновеликие части. Порядок нахождения углов в геометрических фигурах с помощью биссектрис. Методика деления угла на три равные части с использованием способа угла больше развернутого.
статья [1,0 M], добавлен 28.02.2010
Элементарные функции, их анализ. Линейная функция. Квадратичная функция. Степенная функция. Показательная функция (экспонента). Логарифмическая функция. Тригонометрическая функция: синус, косинус, тангенс, котангенс. Обратная функция: аrcsin x, аrctg x.
реферат [325,7 K], добавлен 17.02.2008
Мера ограниченного открытого множества. Мера ограниченного замкнутого множества. Внешняя и внутренняя меры ограниченного множества. Измеримые множества. Измеримость и мера как инварианты движения. Класс измеримых множеств.
Как было показано ранее, функция задает определенное соотношение между двумя числовыми множествами. Однако в некоторых случаях область определения функции может являться множеством чисел, имеющих размерность. В частности, речь идет о множестве значений некоторого угла. Прежде чем приступить к рассмотрению подобных функций, напомним некоторые факты, связанные с измерением углов.
Определение 1. Углом в называется центральный угол, опирающийся на дугу окружности, имеющей длину, равную ее части.
Исторически сложилось деление градуса на 60 минут, а минуты на 60 секунд, то есть: , . Секунды делятся на десятые, сотые и т.д. части. Градус является наиболее распространенной единицей измерения углов.
Определение 2. Углом в 1 радиан называется центральный угол, опирающийся на дугу окружности, имеющую длину, равную ее радиусу .
Таким образом, для отыскания радианной меры центрального угла достаточно длину дуги (l), на которую он опирается, разделить на длину радиуса (R), то есть .
Из сказанного выше следует, что полной окружности будет соответствовать в градусах угол в 360 раз больший, то есть . В радианах это будет радиан. Необходимо также отметить, что величина угла в градусной и радианной мере никак не связана с радиусом окружности. Следовательно, в дальнейшем можно рассматривать окружность любого радиуса, проще всего - единичного.
Формулы перехода от градусной меры дуг и углов к радианной и наоборот имеют вид:
, .
Отсюда следует, что
1 рад = , а рад0,01745 рад.
Рассмотрим теперь координатную плоскость с началом координат в точке О. Проведем окружность единичного радиуса с центром в точке О и отметим точки ее пересечения с осями координат.

Рассмотрим произвольную точку M на окружности и вектор , который называется радиус-вектором точки M.
Будем рассматривать центральные углы AOM, образованные векторами и при перемещении точки M по окружности.
В геометрии
Угол — геометрическая фигура, образованная двумя лучами, которые выходят из одной точки.

В тригонометрии*
Угол — фигура, образованная при повороте луча на плоскости около начальной точки.


2. Измерение углов
Градусная мера углачасть развернутого угла)

Каждому углу ставится в соответствие градусная мера α ∈ [0°; 180°].
Каждому углу как фигуре ставится в соответствие угол поворота, с помощью которого образован этот угол. Угол поворота

Объяснение и обоснование
1. Понятие угла. В курсе геометрии угол определяется как геометрическая фигура, образованная двумя лучами, которые выходят из одной точки. Например, угол AOB, изображенный в первом пункте таблицы 16, — это угол, образованный лучами OA и OB.
Угол можно рассматривать также как результат поворота луча на плоскости около начальной точки. Например, поворачивая луч OA около точки O от начального положения OA до конечного положения OB, также получим угол AOB. Заметим, что достичь конечного положения ОВ можно при повороте луча OA как по часовой стрелке, так и против нее.
2. Измерение углов. Данные выше различные определения угла приводят к различному пониманию измерения углов.
В курсе геометрии каждому углу соответствует его градусная мера, которая может находиться только в пределах от 0° до 180°, и поэтому, например, для прямого угла AOB его мера записывается однозначно: ∠ AOB = 90° (1° — это 1/180 часть развернутого угла).
При измерении углов поворота договорились, что направление поворота против часовой стрелки считается положительным, а по часовой стрелке — отрицательным.

Поэтому при измерении углов, образованных при повороте луча около начальной точки, мы можем получить как положительные, так и отрицательные значения углов поворота. Например, если угол AOB, в котором лучи ОА и ОВ являются взаимно перпендикулярными, получен при повороте луча OA на угол 90° против часовой стрелки, то значение угла поворота β (см. соответствующий рисунок в пункте 2 табл. 16) равно +90° (или просто 90°). Если тот же угол AOB получен при повороте луча OA на угол 270° по часовой стрелке (понятно, что полный оборот — это 360°), то значение угла поворота γ равно (–270°). Этот же угол AOB можно получить также при повороте луча OA против часовой стрелки на 90° и еще на полный оборот; в этом случае значение угла поворота ϕ равно 90° + 360°, то есть 450° и т. д.
Выбрав как значение угла поворота произвольное отрицательное или положительное число (градусов), мы всегда можем повернуть луч OA (по часовой стрелке или против нее) и получить соответствующий угол AOB. Таким образом, величина угла поворота (в градусах) может принимать все действительные значения от.
Для измерения углов принимают определенный угол за единицу измерения и с ее помощью измеряют другие углы.
За единицу измерения можно принять любой угол, например один градус (1°) — 1/180 часть развернутого угла.
В технике за единицу измерения углов принимают полный оборот (заметим, что 1 градус — это 1/360 часть полного оборота).
В мореходстве за единицу измерения углов принимают румб, равный 1/32 час ти полного оборота.
В математике и физике, кроме градусной меры углов, используется также радианная мера углов.
Если рассмотреть некоторую окружность,
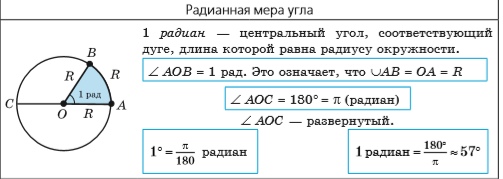
то 1 радиан — это центральный угол, соответствующий дуге, длина которой равна радиусу окружности.
Таким образом, если угол AOB равен одному радиану (рис. 59), то это означает, что ∪AB = OA = R.

Установим связь между радианной и градусной мерами углов. Центральному развернутому углу AOC, с градусной мерой 180°, соответствует полуокружность, то есть дуга, длина которой равна πR, а углу в один радиан — дуга длиной R. Итак, радианная мера развернутого угла AOC равна радиан. Таким образом, одному и тому же развернутому углу АОС соответствует градусная мера 180° и радианная мера π радиан. Это соответствие часто записывают так:
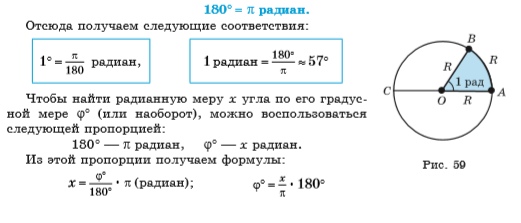
Задача 1 Выразите в радианах величины углов, градусная мера которых равна: 30°; 45°; 60°; 90°; 270°; 360°.
Поскольку 30° — это 1/6часть угла 180°, то из соответствия 180° = π (рад)
получаем, что 30°=6/π (рад).
Аналогично можно вычислить и величины других углов.
В общем случае учитываем, что 1°=π/180 радиан, тогда:

Поскольку радианными мерами рассмотренных углов приходится пользоваться достаточно часто, запишем полученные результаты в виде справочной таблицы:

Задача 2 Выразите в градусах величины углов, радианнная мера которых равна: π/10 ; 2π/3 ; 3π/4 ; 5.
Поскольку π/10 — это 1/10 часть угла π, то из соответствия π = 180° получаем, что π/10=18° . Аналогично можно вычислить и величины углов 2π /3 и 3π/4 .
В общем случае учитываем, что 1 радиан=180°/π , тогда:

Отметим, что далее в этом разделе будет рассматриваться в основном радианная мера угла и утверждения будут доказаны для радианной меры угла. Однако их можно переформулировать и для градусной меры угла, пользуясь приведенными выше соотношениями.
Вопросы для контроля
1. Объясните, как можно определить угол с помощью поворота луча. Как при таком определении измеряются углы?
3. Как можно определить угол в 1°?
4. Дайте определение угла в 1 радиан.
5. Чему равна градусная мера угла в π радиан?
6. Объясните на примерах, как по радианной мере угла найти его градусную меру и наоборот — по градусной мере угла найти его радианную меру.
Упражнения
1°. Изобразите угол, образованный поворотом луча OA около точки O на: 1) 270°; 2) –270°; 3) 720°;
4) –90°; 5) 225°; 6) –45°;
7) 540°; 8) –180°; 9) 360°; 10) –60°.
2°. Чему равны градусные и радианные меры углов поворота, показанных на рисунке 60?

3. Выразите в радианной мере величины углов, градусная мера которых равна:
1 °) 225°; 2°) 36°; 3) 100°; 4) –240°; 5) –22,5°; 6) –150°.
4. Выразите в градусной мере величины углов, радианная мера которых равна:
1) 3π; 2) 3 4 π; 3) −2 5 π;
4) 7 6 π; 5) − π 18 ;
6) 11 6 π;7) −π 8 ; 8) 3.
5. С помощью калькулятора (или таблиц) найдите радианные меры углов, градусная мера которых равна:
1) 27°; 2) 132°; 3) 43°; 4) 114°.
6. С помощью калькулятора (или таблиц) найдите градусные меры углов, радианная мера которых равна:
Помимо градусной меры углов существует так называемая радианная мера. Эта мера широко используется в тригонометрии, в математическом анализе и в его приложениях.
Рассмотрим произвольный положительный угол α . Возьмём на стороне ОА этого угла


– путь, который пройдёт точка М , если произвести указанный поворот α от ОА к ОВ .
Радианной мерой угла α называется отношение этого пути к радиусу ОМ . Радианную меру угла условимся обозначать той же буквой, что и сам угол:



Единицей при радианном измерении углов служит радиан.
Радианом называется центральный угол, опирающийся на дугу окружности, длина которой равна длине радиуса той же окружности.


В основе определения радиана – всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой ( L ) равна длине радиуса ( R ).
Соотношение между радианом и градусом.
На рисунке этот малюсенький угол имеет величину 1 градус :



Действительно, в 180° укладывается 3,1415926 . радиан. Всё время писать 3,1415926 . неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
Вот теперь можно записать приближённое равенство:
180 ° ≈ 3,14 радиан
Или точное равенство:
180 ° = π радиан
Определим, сколько градусов в одном радиане. Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула – это тоже уравнение!) на 3,14 :

Человек видит "Пи" и считает, что это 180 ° . Но "Пи" – это число! Число 3,14 , а никакие не градусы! Это "Пи" радиан = 180° !
Ещё раз: "Пи" – это число! 3,14 . Иррациональное, но число. Такое же, как 5 или 8 . Можно, к примеру, сделать примерно "Пи" шагов. Три шага и ещё немножко. Или купить "Пи" килограммов конфет. Если продавец образованный попадётся.
Перевод градусов в радианы и обратно.
Если угол задан в радианах с числом "Пи", всё очень просто. Мы знаем, что
"Пи" радиан = 180° .
Вот и подставляем вместо "Пи" радиан – 180° . Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов.
Нужно выяснить, сколько градусов в угле "Пи"/2 радиан.


Обратный перевод чуть сложнее. Если угол дан в градусах, мы должны знать, чему равен один градус в радианах, и умножить это число на количество градусов.
Чему равен 1° в радианах ?
Смотрим на формулу и видим, что если 180° = "Пи" радиан, то 1° в 180 раз меньше. Или, другими словами, делим уравнение (формула – это тоже уравнение!) на 180:






Выразить в радианах угол, равный 22 ° 30 ' .
Искомое число радианов получим, умножив

Найти радианную меру угла 12 ° 30 ' с точностью до четвёртого десятичного знака.
Умножим 12 на 0,017453
получим ≈ 0,2094 .
Умножим 30 на 0,000291
получим ≈ 0,00873 .
12 ° 30 ' ≈ 0,2094 + 0,00873 ≈ 0,2181 рад .
Чтобы найти градусную меру любого угла по его данной радианной мере, надо умножить число радиан на

(относительная погрешность результата составит 0,0004% , что составляет абсолютной погрешности 5'' для полного оборота 360 ° ).
Выразить в градусах угол, равный 𝜋 / 12 радианов.

Найти градусную меру угла 1,4 рад с точностью до 1 ' .
Последовательно найдём
1 рад ≈ 57 ° 17'45'',
0,4 рад ≈ 0,4×57 ° .296 = 22 ° .9184,
0 ° .9184×60 ≈ 55'.104,
0'.104×60 ≈ 6''.
Таким образом
0,4 рад ≈ 22 ° 55'6''.
1 рад ≈ 57 ° 17'45'' + 0,4 рад ≈ 22 ° 55'6''
= 1,4 рад ≈ 80 ° 12'51''.
После округления этого результата до требуемой точности в 1' окончательно получим
1,4 рад ≈ 80 ° 13'.
В обозначении меры угла в радианах почти всегда опускают слово >. Таким образом, записи
α = 2, α = 1 / 2 , α = 7 / 9
надо понимать как
α = 2 радиана ,
α = 1 / 2 радиана,
α = 7 / 9 радиана.
Выразить в градусах угол α , равный 2 .
α ≈ 57 ° 3 ∙ 2 ≈ 114 ° 6.
Широко распространено соглашение, по которому под словом > подразумевают не угол как геометрический образ, а число, измеряющее его в радианах или градусах.
Угол π / 2 , угол 36 ° , угол 1 .
В частности, в выражениях типа > под словом > понимается обычно мера угла.
Таблица соотношений между градусным и радианным выражениями некоторых углов.
Для облегчения вычислительной работы при переходе от градусной меры угла к радианной и обратно пользуются специальными таблицами.
Отметим, что радианная мера одного полного оборота


Если углы измерены в градусах, то один полный положительный оборот будет равен 360 ° . Отсюда вытекают следующие соотношения:
360 ° = 2π (≈ 6,2832) радианов,
270 ° = 3 𝜋 / 2 (≈ 4,7124) радианов,
180 ° = π (≈ 3,1416) радианов,
90 ° = 𝜋 / 2 (≈ 1,5708) радианов,
60 ° = 𝜋 / 3 (≈ 1,0472) радианов,
45 ° = 𝜋 / 4 (≈ 0,7854) радианов,
30 ° = 𝜋 / 6 (≈ 0,5236) радианов.
Как пользоваться таблицами Брадиса ?
В книге В. Брадиса > под номером XVI помещена таблица, которая озаглавлена >.
Пометка в скобках расшифровывается так: дуга, содержащая A ° , равна

радианов.
В левом столбце таблицы под буквой А даны числа градусов, содержащихся в угле, а в верхней и самой нижней строках – числа минут, кратных 6.

Угол 71 ° 24' перевести в радианы.
На пересечении строки, начинающейся с 71 ° , и столбца, помещённого вверху 24' , читаем :
(число целых указывается в таблице в начале строки и дальше даются только десятичные знаки).


При переводе в радианы угла с любым числом минут, не кратным 6, пользуются соответствующими поправками, которые помещены в последних трёх столбцах под числами минут:
1', 2', 3'.
Угол 23 ° 20' перевести в радианы.



Найти градусное выражение угла, содержащего 1,0862 радиана.
Имеем из таблицы :





Когда то в Древнем Египте мучились следующим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак. Всё получалось немного больше трёх. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя. В принципе нельзя. Ну, во сколько раз окружность больше диаметра установили. Примерно. В 3,1415926 . раз.
Это и есть число "Пи". После запятой – бесконечное число цифр без всякого порядка. Такие числа называются иррациональными. Это и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.
Для практического применения принято запоминать всего две цифры после запятой:
π = 3,14.
Так как длина окружности больше диаметра в "Пи" раз, имеет смысл запомнить формулу длины окружности:
L = π d
где L – длина окружности, а d – её диаметр.
При радианном измерении углов заметно упрощается ряд формул. Так, для окружности радиуса r длина l его дуги α радиан можно найти по формуле
площадь S сектора круга радиусом r , в дуге которого находится α радиан, вычислим по формуле



Для вычисления дуги окружности и площади сектора, дуги которых (величиной n ° ) измеряются с помощью градусной меры. Эти особенности радианной меры привели к тому, что в тригонометрии отдают преимущество радианному, а не градусному измерении.
Читайте также:

