Преобразование лапласа оригиналы и изображения реферат
Обновлено: 05.07.2024
Преобразование Лапласа — интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.
1. Прямое преобразование Лапласа
Преобразованием Лапласа функции действительной переменной , называется функция комплексной переменной , такая что:
Правая часть этого выражения называется интегралом Лапласа.
2. Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного , называется функция действительного переменного, такая что:
где — некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.
3. Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции участвуют значения x
4. Дискретное преобразование Лапласа
Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают -преобразование и -преобразование.
решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени , где — целое число, а — период дискретизации. Тогда применяя преобразование Лапласа получим:
Если применить следующую замену переменных:
5. Свойства и теоремы
Если интеграл Лапласа абсолютно сходится при σ = σ 0 , то есть существует предел
то он сходится абсолютно и равномерно для и F(s) — аналитическая функция при ( — действительная часть комплексной переменной s). Точная нижняя грань σ a множества чисел σ, при которых это условие выполняется, называется абсциссой абсолютной сходимости преобразования Лапласа для функции f(x).
Условия существования прямого преобразования Лапласа
Преобразование Лапласа существует в смысле абсолютной сходимости в следующих случаях:
Случай : преобразование Лапласа существует, если существует интеграл
Случай σ > σ a : преобразование Лапласа существует, если интеграл
существует для каждого конечного
Случай σ > 0 или σ > σ a (какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции f'(x) (производная к f(x)) для σ > σ a .
Примечание: это достаточные условия существования.
Условия существования обратного преобразования Лапласа
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
1. Если изображение F(s) — аналитичная функция для и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём
аналитична относительно каждого z k и равна нулю для
тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.
Примечание: это достаточные условия существования.
Теорема о свёртке
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
Дифференцирование и интегрирование оригинала
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.
В более общем случае (производная n-го порядка):
Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.
Дифференцирование и интегрирование изображения. Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.
Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.
Запаздывание оригиналов и изображений. Предельные теоремы
Похожие страницы:
Преобразование Лапласа (2)
. по формуле одностороннего преобразования Лапласа , (2.2.11) где р = +j - переменная преобразования Лапласа. Согласно введенным обозначениям . и обратно осуществляется с помощью таблицы преобразования Лапласа. Пример 2.2.1. Найти реакцию инерционного звена .
Лаплас, Пьер-Симон
. , будущий генерал Лаплас, и дочь. 1785: Лаплас становится действительным членом . . Его именем названо преобразование Лапласа и уравнение Лапласа. Он далеко продвинул . методом наименьших квадратов. 2.2. Астрономия Лаплас доказал устойчивость солнечной системы, .
Интегральные преобразования
. уравнений. Обратное преобразование Лапласа. - Это прямое преобразование Лапласа. Обратное преобразование есть возможность получить . формуле : (3) Например : Связь между преобразованиями Фурье и Лапласа. Преобразование Лапласа имеет вид : (1) На f(t) .
Нелинейные и дискретные системы автоматического управления
. используются дискретное преобразование Лапласа, z-преобразование, -преобразование, а также частотные методы. 21.2. Дискретное преобразование Лапласа Дискретное преобразование Лапласа определяется следующим .
Системы с одним и двумя воздействиями
. преобразования Лапласа и легко доказываются. Прямое и обратное преобразования Лапласа функции определяются выражениями , . Преобразование Лапласа . соединение Выразим преобразование Лапласа выходной координаты через преобразование Лапласа входной координаты .
Прямое, обратное, двустороннее и дискретное преобразование Лапласа. Применение преобразования Лапласа. Прямое и обратное преобразования Лапласа некоторых функций. Связь с другими преобразованиями. Преобразование Лапласа по энергии и по координатам.
| Рубрика | Математика |
| Вид | реферат |
| Язык | русский |
| Дата добавления | 26.11.2010 |
| Размер файла | 674,0 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Реферат на тему:
Преобразование Лапласа -- интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией действительного переменного (оригинала). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями.
1. Прямое преобразование Лапласа
Преобразованием Лапласа функции действительной переменной , называется функция комплексной переменной , такая что:
Правая часть этого выражения называется интегралом Лапласа.
2. Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного , называется функция действительного переменного, такая что:
где -- некоторое вещественное число. Правая часть этого выражения называется интегралом Бромвича.
3. Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа -- обобщение на случай задач, в которых для функции участвуют значения x уa: преобразование Лапласа существует, если интеграл
существует для каждого конечного
3. Случай у > 0 или у > уa (какая из границ больше): преобразование Лапласа существует, если существует преобразование Лапласа для функции f'(x) (производная к f(x)) для у > уa.
Примечание: это достаточные условия существования.
· Условия существования обратного преобразования Лапласа
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
1. Если изображение F(s) -- аналитичная функция для и имеет порядок меньше ?1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём
аналитична относительно каждого zk и равна нулю для
тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.
Примечание: это достаточные условия существования.
· Теорема о свёртке
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
· Дифференцирование и интегрирование оригинала
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.
В более общем случае (производная n-го порядка):
Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.
· Дифференцирование и интегрирование изображения. Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.
Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.
· Запаздывание оригиналов и изображений. Предельные теоремы
Примечание: u(x) -- Функция Хэвисайда.
Теоремы о начальном и конечном значении (предельные теоремы):
Все полюсы в левой полуплоскости. Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, к примеру, используется для анализа устойчивости траектории динамической системы.
Умножение на число
6. Прямое и обратное преобразование Лапласа некоторых функций
Ниже представлена таблица преобразования Лапласа для некоторых функций.
Область сходимости для причинных систем
запаздывание n-го порядка с частотным сдвигом
степенная n-го порядка
степенная q-го порядка
единичная функция с запаздыванием
n-го порядка с частотным сдвигом
экспоненциально затухающий синус
экспоненциально затухающий косинус
корень n-го порядка
функция Бесселя первого рода порядка n
модифицированная функция Бесселя первого рода порядка n
функция Бесселя второго рода нулевого порядка
модифицированная функция Бесселя второго рода, нулевого порядка
Примечания к таблице:
· -- постоянная Эйлера -- Маскерони.
· , , и -- вещественные числа.
Причинная система -- система, в которой импульсная передаточная функция h(t) равна нулю для любого момента времени .
7. Применения преобразования Лапласа
Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники.
· Решение систем дифференциальных и интегральных уравнений с помощью преобразования Лапласа легко переходить от сложных понятий математического анализа к простым алгебраическим соотношениям.
· Расчёт передаточных функций динамических систем, таких, к примеру, как аналоговые фильтры.
· Расчёт выходных сигналов динамических систем в теории управления и обработке сигналов -- так как выходной сигнал линейной стационарной системы равен свёртке её импульсной характеристики с входным сигналом, преобразование Лапласа позволяет заменить эту операцию на простое умножение.
· Расчёт электрических схем. Производится путём решения дифференциальных уравнений, описывающих схему операторным методом.
· Решение нестационарных задач математической физики.
8. Связь с другими преобразованиями
Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.
Преобразование Лапласа-Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную.
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа связано с односторонним с помощью следующей формулы:
Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом s = iщ:
Примечание: в этих выражениях опущен масштабирующий множитель
который часто включается в определения преобразования Фурье.
Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.
Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина
положим и = e ? x , то получим двустороннее преобразование Лапласа.
Z-преобразование -- это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных:
где -- период дискретизации, а -- частота дискретизации сигнала. Связь выражается с помощью следующего соотношения:
Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.
9. Преобразование Лапласа по энергии
для моноэнергетического источника S(E)=(E-E0) с интегральным членом в форме:
и, не пренебрегая для простоты зависимостью сечений У(E) и
от E, перейдем от E к новой переменной
Решение этого уравнения можно получить с помощью преобразования Лапласа по энергии:
Его можно рассматривать как разложение дифференциальной плотности потока по системе биортогональной функции и .
Подействуем на все члены уравнения (1) оператором
В соответствии с (3) первый член преобразования к виде
Во втором члене необходимо изменить порядок интегрирования и в интеграле по сделать замену переменных
Тогда он приведется к виду
-трансформанта Лапласа от дифференциального сечения рассеяния.
Правая часть уравнения (1) легко преобразуется, после чего получаем
Подставляя (5) в (2), находим интересующую нас функцию Ф():
быстро убывает с ростом Q экспоненту в (4) можно разложить в ряд.
где -середина потери энергии на единице длины пути. Подставим это разложение в (6) и сделаем замену переменных
Тогда (6) перейдет в:
Вычисляя, интеграл с помощью вычетов и возвращаясь от переменной к переменной E, получаем:
Экспонента в формуле (7) есть вероятность того, что частица избежит поглощения на пути, где энергия меняется от Е0 до Е. Если сечение поглощения равно нулю, то
Формула (8) имеет простой физический смысл. По определению Ф(E)=dE есть средний путь, пройденный частицей за время, пока ее энергия меняется от E+dE до E.
В приближении непрерывного замедления dE/dl=, откуда dl/dE=1/, что совпадает с (8).
10. Преобразование Лапласа по координатам
Поскольку частицы испускаются в положительном направлении оси Оz, в области z0 плотность потока равна 0 и область изменения z в уравнении (208) следует считать полубесконечный интервал (0,). Это обстоятельство позволяет применить для решения уравнения (208) преобразование Лапласа по координатам:
где трансформанта Лапласа Ф(,E) выражается через плотность потока следующим образом:
Умножим обе части уравнения (208) на и проинтегрируем по z от 0 до . Преобразовав первый член интегрированием по частям с учетом граничного условия (209) и, использовав обозначение (211), получим:
После преобразования Лапласа остальных членов уравнения (208) приходим к уравнению для трансформанты плотности потока:
которое в отличие от (208) не содержит производных и является интегральным уравнением типа уравнения деградации энергии. Введя обозначение
Перепишем уравнение (312) в виде
При действительных уравнение (214) по форме совпадает с уравнением деградации энергии для частиц с макроскопическим сечением столкновений и дифференциальным сечением рассеяния
Из (213) видно, что по мере уменьшения обращается в нуль, а потом становится отрицательной. Отсюда следует, что решение уравнения (214) существует лишь в области
Если выполняется условие
то для трансформанты рассеянной компоненты плотности потока получим
Если и C не зависят от энергии, формула (215) упрощается:
Перейдем к восстановлению энергетического спектра рассеянных частиц:
Тогда формула (217) примет вид:
Функция , представляющая собой обратное преобразование Лапласа функции s -2 exp(a/s),равна
где I1- модифицированная функция Бесселя первого порядка. Таким образом
В частности, при малых значениях аргумента I1(x), поэтому
При больших значениях аргумента , следовательно,
Из (219)-(221) видно, что с увеличением z отношение рассеянного излучения к нерассеянному возрастет сначала линейно (когда главную роль играет однократное рассеяние), затем более сложным образом, причем низкоэнергетическая часть спектра, обусловленная многократным рассеянием, растет быстрее высокоэнергетической.
Подобные документы
Описание уравнениями в конечных разностях динамических процессов в дискретных системах управления. Операционный метод решения разностных уравнений, основанный на дискретном преобразовании Лапласа. Обобщение обычного преобразования на дискретные функции.
реферат [61,7 K], добавлен 21.08.2009
Математический анализ и операционное исчисление. Обращение преобразования с помощью многочленов, ортогональных на промежутке. Интегральное преобразования Лапласа с помощью смещенных многочленов Лежандра и многочленов Чебышева первого рода.
реферат [503,6 K], добавлен 10.02.2011
Дискретный периодический сигнал, представленный рядом Фурье. Прямое и обратное дискретное преобразование. Его свойства: линейность и симметрия. Алгоритм вычисления круговой свертки сигналов. Равенство Парсеваля для них. Связь ДПФ с Z-преобразованием.
презентация [72,0 K], добавлен 19.08.2013
Однородный Марковский процесс. Построение графа состояний системы. Вероятность выхода из строя и восстановления элемента. Система дифференциальных уравнений Колмогорова. Обратное преобразование Лапласа. Определение среднего времени жизни системы.
контрольная работа [71,2 K], добавлен 08.09.2010
Решение системы линейных обыкновенных дифференциальных уравнений, описывающей боковое перемещение нестабильного самолета относительно заданного курса полета методом преобразования Лапласа. Стабилизация движения путем введения отрицательной обратной связи.
курсовая работа [335,8 K], добавлен 31.05.2016
Статическая характеристика элемента. Выполнение аналитической линеаризации заданной функции в определенной точке. Обратное превращение Лапласа заданной передаточной функции ОАУ. Преобразование дифференциального уравнения к нормальной форме Коши.
контрольная работа [564,9 K], добавлен 30.03.2015
Идея и возможности вейвлет-преобразования. Свойства вейвлетов: непрерывное прямое и обратное образование. Понятие и оценка преимуществ, сферы применения дискретного вейвлет-преобразования. Поиск изображений по образцу. Многомасштабное редактирование.
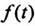
Функцией- оригиналом - называют функцию действительного аргумента
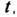
удовлетворяющую условиям:
1) для всех отрицательных значений аргумента функция тождественно равна нулю, т.е.
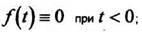
2) функция при возрастает не быстрее показательной функции, т.е. существ.уют такие постоянные что
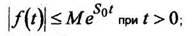
3) на любом конечном отрезке положительной полуоси функция и ее производные достаточно высокого порядка непрерывны или имеют конечное число разрывов 1-го рода.
Простейшей функцией - оригиналом является единичная функция Хевисайда
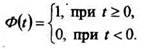
(1)
Если функция не удовлетворяет условию то произведение уже ему удовлетворяет, т.е. будет оригиналом.
Для простоты записи множитель опускается, например, пишут вместо вместо и т.д.
Изображением функции по Лапласу (преобразованием по Лапласу) называют функцию комплексной переменной определяемую соотношением
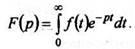
(2)
Интеграл (1.2) называют интегралом Лапласа.
Функция определяется в полуплоскости и является в этой области аналитической функцией.
То, что функция комплексной переменной является изображением по Лапласу функции действительного аргумента обозначается или
Изображение элементарных функций получается непосредственно с помощью интеграла (2).
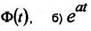
Пример 1 Найти изображение по Лапласу функции
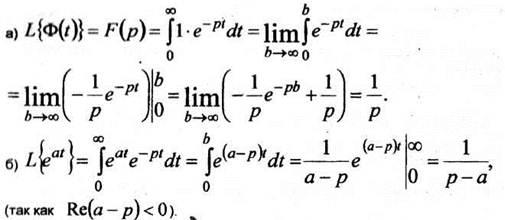
Таким образом, получаем
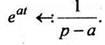
Преобразование, основанное на интеграле Лапласа (2), обладает линейными свойсгыами.
1. Преобразование суммы функций равно сумме преобразований этих функций
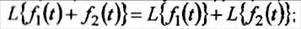
2 Постоянный множитель можно выносить за знак преобразования:
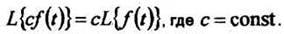
Из этих двух свойств следует, что линейной комбинации оригиналов соответствует линейная комбинация их преобразований:
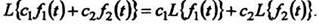
(3)
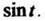
Пример 2. Найти изображение функции
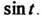
Используем формулу (2) для функции Тогда
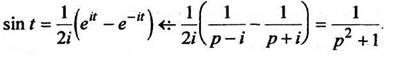

1. Теорема подобияЕсли то для любого постоянногоа > 0
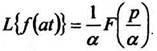
(4)
Пример 3. НайдемИз примера2 .По Формуле (4)
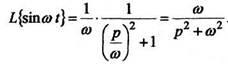
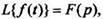
2.Дифференцирование оригиналаЕсли то
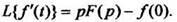
(5)
Методом индукции на основании формулы (5) получены формулы изображения высших производных:
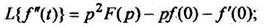
(6)
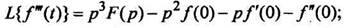
(7)

(8)
Пример 4. ОпределимТак как
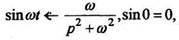
то по формуле (5) получим:
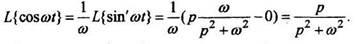
3. Дифференцирование изображения.Если то т.е. дифференцирование изображения сводится к умножению на оригинала. В общем случае,

(9)
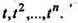
Пример 5. Определить изображения функций

Так как

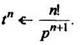
В общем случае
4. Интегрирование оригинала.Интегрирование оригинала сводится к делению изображения на р:
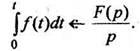
(10)
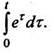
Пример 6. Найти изображение функци
РЕШЕНИЕ Так как то по формуле (10)
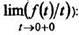
5. Интегрирование изображения.Интефирование изображения равносильно делению на tоригинала (если существует конечный предел
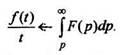
(11)
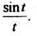
Пример 7. Найдем изображение функции
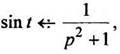
Так как то по формуле (11) получаем

6. Теорема смещенияПри умножении оригинала на изображение получается смещение аргумента на
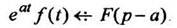
(12)
Пример 8. В примерах 3, 4, 5 найдены изображения функций По формуле (12) находим:
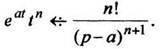
7. Теорема запаздывания."Включение" оригинала с запаздыванием на равносильно умножению изображения на

(13)
В данной формуле важно подчеркнуть, что функция поэтому она умножена на единичную функцию Хевисайда с запаздыванием .График единичной функции Хевисайда с запаздывающим аргументом показан на рисунке 1.
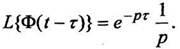
Изображение
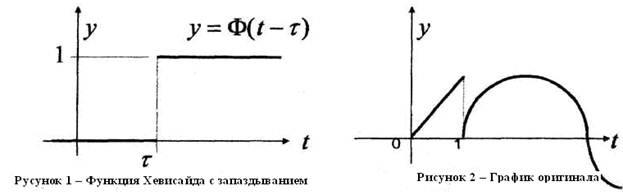

Свертка односторонних функций, ее свойства. Теорема Бореля
Сверткой функций и , заданных на , называется функция, равная интегралу , ; она обозначается , т.е.
, . (21)

Свойства свертки

1. Симметрия, т.е. .

В самом деле, изменяя порядок интегрирования и полагая , получаем равенство
.
2. Если и – оригиналы, то и их свертка также является оригиналом с показателем роста, равным наибольшему из показателей роста функций и . Рекомендуем доказать самостоятельно это утверждение или же посмотреть в [3].
ПРИМЕР 32. Найти свертку функций и .

Решение. , здесь ко второму интегралу применено интегрирование по частям.
Если функции и – оригиналы и , и , , то произведение изображений является изображением свертки соответствующих оригиналов для :

. (22)
В самом деле, по определению изображения имеем

.

Замечаем, что справа стоит двойной интеграл с областью интегрирования , изображенной на рисунке. Изменяя в этом интеграле порядок интегрирования, получаем
.

Замена переменной интегрирования позволяет записать

.
Поскольку внутренний интеграл не зависит от , а внешний от , то двойной интеграл равен произведению двух интегралов, т.е.

.
Теорема Бореля применяется для нахождения оригинала в случае, когда изображение представлено в виде двух множителей, для каждого из которых оригинал устанавливается.
Пусть имеем линейное неоднородное уравнение с постоянными коэффициентами:

где функция удовлетворяет условиям, налагаемым на оригиналы.
Уравнение (38) надо решить при нулевых начальных условиях

Применяя к обеим частям уравнения (38) преобразование Лапласа и учитывая начальные условия, найдем согласно (12):

,


.
Из равенства (40), пользуясь известными приемами операционного исчисления, рассмотренными выше, найдем по изображению оригинал , который и будет являться искомым решением уравнения (38) при .
Если уравнение (40) требуется решить при ненулевых начальных условиях

,

то после применения к (40) преобразования Лапласа найдем согласно (11):

где известная целая рациональная функция от .

откуда определим оригинал , являющийся искомым решением уравнения (38).
Нетрудно видеть, что в случае однородного уравнения

оставим систему уравнений:

Решив ее, получаем


Итак X(p)= , откуда

x(t)=— решение данного дифференциального уравнения.
Системы линейных дифференциальных уравнений с постоянными коэффициентами можно решать операционными методами совершенно так же, как и отдельные уравнения; все отличие заключается лишь в том, что вместо одного изображающего уравнения приходим к системе таких уравнений, причем система эта в отношении изображений искомых функций будет линейно алгебраической. При этом никаких предварительных преобразований исходной системы дифференциальных уравнений производить не требуется [3, с. 134].
Читайте также:

