Построение углов по клеточкам реферат
Обновлено: 02.07.2024
Почему тетради по математике в клетку? Наверное, чтобы удобнее было записывать в столбик числа. А еще, чтобы легче было чертить. Клеточки на бумаге позволяют многие построения проводить только с помощью одной линейки, причем на этой линейке может даже не быть делений. Мы уже можем строить на клетчатой бумаге отрезок заданной длины, прямоугольник, если известна его ширина и длина, квадрат с известной стороной. То есть обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур.
Стало интересно, а можно ли построить параллелограмм, трапецию, треугольник? У всех этих фигур стороны проходят не по линиям сетки клетчатой бумаги, а пересекают их. Или, можно сказать, стороны находятся под углом друг к другу (отличного от 90). Поэтому, в первую очередь, мы должны научиться строить углы, используя только клетки.
Оценить 348 0
Научно - исследовательская работа
Мурзинова Ксения Евгеньевна
учащаяся 8 класса
Руководитель:
Аршина Алена Геннадьевна
учитель математики высшей квалификационной категории
История геометрических измерений углов………………..……5
Экспериментальная часть…………… …………………………..7
Почему тетради по математике в клетку? Наверное, чтобы удобнее было записывать в столбик числа. А еще, чтобы легче было чертить. Клеточки на бумаге позволяют многие построения проводить только с помощью одной линейки, причем на этой линейке может даже не быть делений. Мы уже можем строить на клетчатой бумаге отрезок заданной длины, прямоугольник, если известна его ширина и длина, квадрат с известной стороной. То есть обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур.
Стало интересно, а можно ли построить параллелограмм, трапецию, треугольник? У всех этих фигур стороны проходят не по линиям сетки клетчатой бумаги, а пересекают их. Или, можно сказать, стороны находятся под углом друг к другу (отличного от 90). Поэтому, в первую очередь, мы должнынаучиться строить углы, используя только клетки.
Цель:найти способ построения углов без транспортира на клетчатой бумаге.
построить острые углы на клетчатой бумаге (от 10 до 80, кратных 10) и исследовать их расположение по отношению к узлам сетки;
составить таблицу решений исследуемой задачи;
проверить полученные результаты с помощью ПО GeoGebra
определить группы задач, которые можно решить с помощью исследованного метода построения углов;
Объект исследования: острые углы с градусной мерой, кратной 10;
Предмет исследования: процесс построения углов на клетчатой бумаге без использования транспортира;
Гипотеза: можно предположить, что существуют углы разных градусных мер, которые можно построить без транспортира, пользуясь только линейкой без мерных делений и клетчатой бумагой;
Практическая значимость:
Для построения углов, с градусными мерами, кратными 10 не требуется наличие транспортира;
С помощью предложенного метода можно выполнять чертежи геометрических фигур (треугольников, трапеции) с заданными мерами углов;
Данный метод позволяет начертить геометрические фигуры на местности или на бумаге большого формата, так как размер клетки может быть произвольным.
Новизна работы:
описанный метод построения углов без транспортира не используется на уроках; нет описания этого приема и в математической литературе.
Основная часть
Первые задачи на построение углов возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией. Первые греческие ученые, которые занимались решением геометрических задач на построение, были: Фалес Милетский (624 – 547 гг. до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.). Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим. Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии. Известны приборы для измерения углов …
Экспериментальная часть
Для проведения исследования на листке клетчатой бумаги построили острые углы, начиная от 10 до 80, с интервалом в 10. Центр угла был расположен в узле клетки. Один из лучей, образующих угол, провели горизонтально слева направо. Далее с помощью транспортира начертили лучи для всех исследуемых углов.


В результате получилась такая таблица
Для углов от 20 до 70 количество клеток вверх на единицу превышает количество десятков в градусной мере угла. Причем сумма клеток вверх и вправо для всех этих углов равна 11.

Мы выбрали именно эту тему, потому что стало интересно, почему же мы для работы по геометрии используем тетрадь именно в клетку. Ведь существует много видов тетрадей: в клеточку, в линеечку, в ромбик, в кружочек. Но почему-то именно в тетради в клетку мы решаем различные геометрические задачи и строим геометрические фигуры. Мы хотим выяснить, помогает ли клетка при выполнении таких заданий и как еще можно использовать тетрадку в клетку?
Исторические факты о тетрадях.
В городе Мышкин Ярославской области, есть единственный в России музей школьных тетрадей. В коллекции - диктанты, изложения, математические примеры, и современные и написанные несколько веков назад.
Всего в коллекции музея около тысячи тетрадей по самым разным предметам.

Исторические факты о тетрадях.
Такая бумага, какой мы её знаем сегодня появилась в России только в середине XVI века, но расцвет бумажного производства наступил при Петре Первом. По его указу были построены первые предприятия по производству бумаги под Москвой и Санкт-Петербургом.
Тетради отечественного производства появились в России только в начале XVIII века.
В Советском Союзе у всех школьников были одинаковые тетради.
Сегодня же в магазинах – огромный выбор тетрадей, в том числе и тетрадей в клеточку.
Такая бумага, какой мы её знаем сегодня появилась в России только в середине XVI века, но расцвет бумажного производства наступил при Петре Первом. По его указу были построены первые предприятия по производству бумаги под Москвой и Санкт-Петербургом.

Цель и задачи проекта:
- Цель: выяснить, помогает ли клетка в выполнении математических построений и вычислений.
- Задачи:
1. Узнать свойства клетки как геометрической фигуры.
2. Научиться решать геометрические задачи с помощью свойств клетки.

Свойства клетки как квадрата.
- Для того, чтобы понять, почему тетрадь по математике в клетку, я решила узнать побольше о квадрате. Я нарисовала квадрат.
Как мы знаем, квадрат обладает всеми свойствами прямоугольника и ромба. Следовательно, у квадрата есть 3 основных свойства:
Использование тетради в клетку в геометрии:
Тетрадь в клетку очень удобна для занятия геометрией. Она помогает при построении различных геометрических фигур , при этом используются узлы клеток:
Определение: две прямые, образующие при пересечении прямые углы, называют перпендикулярными.
На рисунке прямая a⊥с

Для построение параллельных прямых.
Определение: две непересекающиеся прямые на плоскости называют параллельными.
На рисунке прямые a∥t.
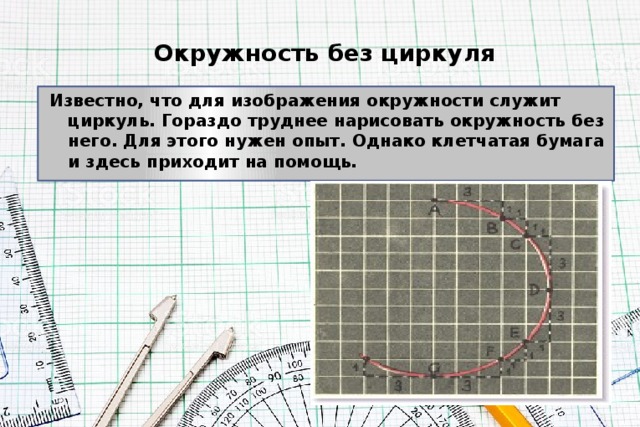
Окружность без циркуля
Известно, что для изображения окружности служит циркуль. Гораздо труднее нарисовать окружность без него. Для этого нужен опыт. Однако клетчатая бумага и здесь приходит на помощь.

Могут ли клетки помочь с вычислением площадь многоугольника?
Оказывается, могут. Давайте разберём, как же клетки могут помочь нам.
Площадь многоугольника на клетчатой бумаге измеряется квадратными единицами: мм 2 , см 2 . Но в качестве единицы площади можно рассматривать и клетку .
Нарисуем многоугольник с вершинами в узлах клеток и найдём его площадь. Это можно сделать разными способами.

Разделим многоугольник на части и составим из них равновеликий многоугольник с вершинами в узлах клеток, стороны которого проходят по линиям. В полученном многоугольнике легко посчитать количество клеток , то есть площадь многоугольника.
Будем пользоваться следующими правилами:
Этот способ вычисления площади легко применим для многоугольников несложной конфигурации. А если он выглядит более причудливо?
Оказывается, площади многоугольников, вершины которых расположены в узлах клетки, можно вычислить гораздо проще: есть формула, связывающая их площадь с количеством узлов, лежащих внутри и на границе многоугольника. Эта замечательная и простая формула называется формулой Пика.

- Теорема Пика. ПустьL— число целочисленных точек внутри многоугольника,B— количество целочисленных точек на его границе,S— его площадь. Тогда справедлива формула Пика:
Найдите площадь четырёхугольника АВСD.
Решение: Для многоугольника на рисунке L=23 (желтые точки), B=7 (синие точки, не забудьте о вершинах!).
По формуле Пика:
Ответ: S=25,5 квадратных единиц.

Найдите площадь параллелограмма АВСD
L=6,B=6; по формуле Пика:
S=6+6/2-1=8 (см 2 )
Ответ: 8 см 2
Найдите площадь четырёхугольника АВСD
L=5,B=7;по формуле Пика:
Ответ: 7,5см 2
Игры на клетчатом листе.
А вы знали, что на клетчатом листе можно играть в разные логические игры. Мы уверены, что да. Вот несколько таких игр:
Игры на клетчатом листе.
Крестики-нолики.
- Игроки по очереди ставят на свободные клетки поля 3х3 знаки (один всегда крестики, другой всегда нолики). Первый, выстроивший в ряд 3 своих фигур по вертикали, горизонтали или диагонали, выигрывает.
Игры на клетчатом листе.
Морской бой.
Игры на клетчатом листе.
Линии противников нигде не должны пересекаться.
Игры на клетчатом листе.
У каждого игрока должна быть ручка или карандаш своего цвета. По очереди игроки ставят точки в произвольных местах на пересечении клеток. Цель игры – захватить как можно больше бумажных владений. Территория считается захваченной, если она обнесена точками своего цвета. Точки должны располагаться друг от друга на расстоянии в одну клеточку по горизонтали, вертикали или диагонали. Захваченная территория закрашивается своим цветом или вокруг нее рисуется крепости.

Клетка для развития детей.

Клетка для развития детей.
Разрезание фигуры
Данный задания не имеют общего метода решения, что обуславливает их ценность для развития не конкретного учебного умения или навыка, а вообще умение думать, размышлять, анализировать, искать аналогии, то есть они развивают мыслительные навыки в самом их широком понимании.
Задача: Фигуру разрезать на 4, равных по площади фигурки (не обязательно на прямоугольники).

Клетка для развития детей.
Задача: На координатной плоскости постройте точки и последовательно их соедините
1) (2; -3), (2; -2), (4; -2), (4; -1), (3; 1), (2; 1), (1; 2), (0; 0), (-3; 2), (-4; 5), (0;8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7;0), (6; 2), (6; 2), (5; -3), (2; -3).
2) (4; -3), (4; -5), (3; -9), (0; -8), (1; -5), (1; -4), (0; -4), (0; -9), (-3; -9), (-3; - 3), (-7; -3), (-7; -7), (-8; -7), (-8; -8), (-11; -8), (-10; -4), (-11; -1), (-14; -3), (-12; -1), (-11;2), (-8;4), (-4;5).

В ходе создания проекта мы изучили свойства клетки как геометрической фигуры. С их помощью мы научились на клетчатой листе:
- строить перпендикулярные и параллельные прямые;
- строить различные геометрические фигуры;
- вычислять площади многоугольников с вершинами в узлах клеток;
- играть в различные игры.
Анализируя все полученные результаты, мы сделали вывод:
тетрадь в клетку помогает в математических построениях, вычислениях, а также весело и интересно проводить свободное время.
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки. Углы измеряются в градусах и радианах. Угол, образованный продолжением сторон данного угла, называется вертикальным к данному. Угол, образованный одной из сторон данного угла и продолжением другой стороны, называется смежным с ним. Приспособление для построения углов на чертежах, называется транспортир.
Значение геометрии в развитии математике
Применение евклидовой геометрии представляет самое обычное явление всюду, где определяются площади, объемы и т. п. Геометрия изучает пространственную непрерывность. Общая роль геометрии в математике состоит также в том, что с нею связано идущее от пространственных представлений точное синтетическое мышление, часто позволяющее охватить в целом то, что достигается анализом и выкладками лишь через длинную цепь шагов. Геометрия характеризуется не только своим предметом, но и методом, идущим от наглядных представлений и оказывающимся плодотворным в решении многих проблем других областей математики. Геометрия имела решающее значение в возникновении и развитии анализа. Интегрирование происходит от нахождения площадей и объемов. Графическое представление функций сыграло важную роль в выработке понятий анализа и сохраняет свое значение. Геометрия оказывает влияние на алгебру, и даже на арифметику – теорию чисел, поэтому роль геометрии в развитии математике очень велика.
Цель работы: найти способ построения углов без транспортира.
Гипотеза: Любой острый угол можно построить без транспортира по узлам клетки.
• рассмотреть углы и найти их связь с узлами клеток.
Построим с помощью транспортира углы от 10° до 80° со стороной, идущей по горизонтальной линии сетки.
Отметим у каждого угла ближайший узел сетки, через который прошла другая сторона каждого угла.
Величина угла Клеток → Клеток ↑
Если сравнить данные таблицы для углов 10° и 80°, 20° и 70°, 30° и 60°, 40° и 50°, то можно заметить, что количество клеток вправо и количество клеток вверх меняются местами.
Используя данные таблицы, можно приближенно построить любой острый угол без транспортира.
Таким образом, обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур. В 7 классе мы начинаем изучать геометрию и, полученными результатами, можно будет пользоваться при изучении курса планиметрии для построения схематических чертежей, точнее соответствующих условию задач.
Также, выполняя презентацию работы, я совершенствовала свои навыки работы на компьютере.

Почему тетради по математике в клетку? Наверное, чтобы удобнее было записывать в столбик числа. А еще, чтобы легче было чертить. Клеточки на бумаге позволяют многие построения проводить только с помощью одной линейки, причем на этой линейке может даже не быть делений. Мы уже можем строить на клетчатой бумаге отрезок заданной длины, прямоугольник, если известна его ширина и длина, квадрат с известной стороной. То есть обычный лист бумаги в клетку может выполнять функцию своеобразного инструмента для построения геометрических фигур.
Стало интересно, а можно ли построить параллелограмм, трапецию, треугольник? У всех этих фигур стороны проходят не по линиям сетки клетчатой бумаги, а пересекают их. Или, можно сказать, стороны находятся под углом друг к другу (отличного от 90). Поэтому, в первую очередь, мы должнынаучиться строить углы, используя только клетки.
Цель: найти способ построения углов без транспортира на клетчатой бумаге.
построить острые углы на клетчатой бумаге (от 10 до 80, кратных 10) и исследовать их расположение по отношению к узлам сетки;
составить таблицу решений исследуемой задачи;
проверить полученные результаты с помощью ПО GeoGebra
определить группы задач, которые можно решить с помощью исследованного метода построения углов;
Объект исследования: острые углы с градусной мерой, кратной 10;
Предмет исследования: процесс построения углов на клетчатой бумаге без использования транспортира;
Гипотеза: можно предположить, что существуют углы разных градусных мер, которые можно построить без транспортира, пользуясь только линейкой без мерных делений и клетчатой бумагой;
Практическая значимость:
Для построения углов, с градусными мерами, кратными 10 не требуется наличие транспортира;
С помощью предложенного метода можно выполнять чертежи геометрических фигур (треугольников, трапеции) с заданными мерами углов;
Данный метод позволяет начертить геометрические фигуры на местности или на бумаге большого формата, так как размер клетки может быть произвольным.
Новизна работы:
описанный метод построения углов без транспортира не используется на уроках; нет описания этого приема и в математической литературе.
Основная часть
Первые задачи на построение углов возникли в глубокой древности. Возникли они из хозяйственных потребностей человека. Уже древними архитекторами и землемерами приходилось решать простейшие задачи на построение, связанные с их профессией. Первые греческие ученые, которые занимались решением геометрических задач на построение, были: Фалес Милетский (624 – 547 гг. до н.э.), Пифагор (ок. 580 – 500 гг. до н.э.), Платон (427 – 347 гг. до н.э.). Платон и его ученики считали построение геометрическим, если оно выполнилось при помощи циркуля и линейки, то есть путем проведения окружностей и прямых линий. Если же в процессе построения использовались другие чертежные инструменты, например транспортир, то построение не считалось геометрическим. Древние греки вслед за Платоном стремились к геометрическим построениям и считали их идеалом в геометрии. Известны приборы для измерения углов …
Экспериментальная часть
Для проведения исследования на листке клетчатой бумаги построили острые углы, начиная от 10 до 80, с интервалом в 10. Центр угла был расположен в узле клетки. Один из лучей, образующих угол, провели горизонтально слева направо. Далее с помощью транспортира начертили лучи для всех исследуемых углов.


В результате получилась такая таблица
Для углов от 20 до 70 количество клеток вверх на единицу превышает количество десятков в градусной мере угла. Причем сумма клеток вверх и вправо для всех этих углов равна 11.
Построение чертежа на клетчатой бумаге или на координатной плоскости с выделенными целочисленными координатами характеристических точек фигуры или графика функции. Построение описанной окружности девяти точек для треугольников с углом 45 или 135 градусов.
| Рубрика | Математика |
| Вид | статья |
| Язык | русский |
| Дата добавления | 25.02.2016 |
| Размер файла | 363,8 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
HTML-версии работы пока нет.
Cкачать архив работы можно перейдя по ссылке, которая находятся ниже.
Подобные документы
Определение производных сложных функций при заданном значении аргумента. Исследование траектории движения тела на плоскости и построение графика функции. Характеристика нахождения максимальных и минимальных точек, экстремумов и точек перегиба функции.
контрольная работа [790,1 K], добавлен 09.12.2011
Плоскость как простейший вид поверхности, ее задание тремя точками. Основные геометрические фигуры на плоскости. Определение геометрического места точек, примеры для угла и окружности. Сущность использования метода геометрических мест при решении задач.
курсовая работа [115,2 K], добавлен 10.01.2010
Треугольник как геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки. Основные элементы данной фигуры: вершины и стороны. Классификация и разновидности треугольников по различным признакам.
презентация [343,2 K], добавлен 28.11.2013
Окружность множество точек плоскости, равноудаленных от данной точки. Эллипс, множество точек плоскости, для каждой из которых сумма расстояний до двух точек плоскости. Парабола, множество точек плоскости, равноудаленных от данной точки плоскости.
реферат [197,7 K], добавлен 03.08.2010
Построение угла равного данному, биссектрисы данного угла, середины отрезка, перпендикулярных прямых, треугольника по трем элементам. Теорема Фалеса и геометрическое место точек. Построение с использованием свойств движений. Метод геометрических мест.
Читайте также:

