Параллельность и перпендикулярность в пространстве реферат
Обновлено: 02.07.2024
Перпендикулярные прямые в пространстве. Определение и признак прямой, перпендикулярной к плоскости. Теорема о перпендикулярности двух параллельных, двух перпендикулярных прямых к плоскости. Перпендикуляр и наклонные. Угол между прямой и плоскостью.
| Рубрика | Математика |
| Вид | презентация |
| Язык | русский |
| Дата добавления | 20.11.2014 |
| Размер файла | 160,5 K |
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
HTML-версии работы пока нет.
Cкачать архив работы можно перейдя по ссылке, которая находятся ниже.
Подобные документы
Перпендикулярные прямые в пространстве. Лемма о перпендикулярности двух параллельных прямых к третьей прямой. Параллельные прямые, перпендикулярные к плоскости. Признаки перпендикулярности плоскостей. Построение перпендикуляра в многомерных пространствах.
презентация [1,6 M], добавлен 14.12.2012
Возможные случаи ориентации прямой и плоскости для заданного уравнения. Условия их перпендикулярности и параллельности. Скалярное произведение перпендикулярных векторов. Координаты точки, лежащей на прямой. Угол между прямой и плоскостью, его определение.
презентация [65,2 K], добавлен 21.09.2013
Понятие параллельности как отношения между прямыми. Случаи расположения прямой и плоскости. Признаки параллельности прямой и плоскости. Основные свойства двух прямых. Отсутствие общих точек у прямой и плоскости. Признаки параллельности плоскостей.
презентация [1,5 M], добавлен 14.10.2014
Общая характеристика примеров нахождения точки пересечения двух прямых. Знакомство с условиями параллельности и перпендикулярности прямых, рассмотрение особенностей решения уравнений. Анализ способов нахождения углового коэффициента искомой прямой.
презентация [97,6 K], добавлен 21.09.2013
Способы определения плоскости. Прямые в пространстве, признаки их параллельности, пересечения, скрещивания. Принадлежность прямой плоскости, их параллельность и скрещивание. Перпендикулярность прямой и плоскости. Взаимодействие плоскостей в пространстве.
презентация [1,4 M], добавлен 13.04.2016
Доказательство теоремы о том, что любая точка перпендикуляра, проходящего через середину данного отрезка, равноудалена от его концов, и что если данная точка равноудалена от концов отрезка, то она лежит на прямой, перпендикулярной данному отрезку.
презентация [71,5 K], добавлен 02.12.2010
Уравнение плоскости, проходящей через точку параллельно горизонтальной, фронтальной и профильной прямым. Угол в точке пересечения прямой с плоскостью. Условия параллельности и перпендикулярности прямой и плоскости. Метод прямоугольного треугольника.
Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.
Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.




Две плоскости называются параллельными, если они не пересекаются.
Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как
Отрезки параллельных прямых между параллельными плоскостями равны.

= =
Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

.
Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.
Перпендикуляр, опущенный из данной точки на данную плоскость, - это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра - это его конец, лежащий в плоскости.
Расстояние от точки до плоскости - это длина перпендикуляра, опущенного от этой точки на плоскость.
Наклонная, проведенная из данной точки к данной плоскости, - это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, - это основание наклонной. Проекция наклонной - это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.
1. Теорема о проецировании прямого угла
Возможны три случая проецирования прямого угла:
1. Если обе стороны прямого угла прямые общего положения, то прямой угол проецируется искаженно на все три плоскости проекций.
2. Если обе стороны прямого угла параллельны какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину.
3. Если одна сторона прямого угла параллельна какой-либо плоскости проекций, то прямой угол проецируется на эту плоскость в натуральную величину, рис. 64. Это основная теорема о проецировании прямого угла.

Дано: ÐАВС = 90°; ВСúú Н. Необходимо доказать: ÐА ¢В ¢С ¢ = 90°.
1. ВС ^АВВ ¢А ¢
ВС ^АВ , следовательно ВС ^ВВ ¢ - по свойству ортогонального проецирования
2. В ¢С ¢úúВС
3. В ¢С ¢^АВВ ¢А ¢
4. В ¢С ¢^А ¢В ¢ - что и требовалось доказать
2. Главные линии плоскости
Линии уровня плоскости
Кроме прямых линий общего положения, в плоскости отмечают три главные линии: горизонтальную (горизонталь), фронтальную (фронталь) и линию наибольшего наклона. Эти линии применяют как вспомогательные: они упрощают решение задач. Две из них — горизонтальная и фронтальная — уже рассматривались.
Необходимо добавить, что все горизонтальные линии плоскости параллельны между собой, а их горизонтальные проекции параллельны горизонтальному следу плоскости (рис. 65). Горизонтальный след плоскости — одна из горизонталей.
 |  |
| Рис. 64 | Рис. 65 |
Все фронтальные линии плоскости параллельны между собой, а их фронтальные проекции параллельны фронтальному следу плоскости. Фронтальный след плоскости — одна из фронтальных линий (рис. 66).

Линии наибольшего наклона плоскости
Прямые плоскости, перпендикулярные к прямым уровня этой плоскости, называются линией наибольшего наклона (ЛНН) данной плоскости к соответствующей плоскости проекций.
Линии наибольшего наклона плоскости перпендикулярны к ее следам или к линиям уровня (либо к ее горизонталям, либо к фронталям, либо к ее профильным прямым) (рис. 67).
В случае перпендикулярности к горизонтали определяется наклон к плоскости проекций H (при этом ЛНН называют линией наибольшего ската ), перпендикулярности к фронтали — наклон к плоскости проекций V, перпендикулярности к профильной прямой — наклон к плоскости проекций W.
На рис. 67, 68 дано изображение плоскости (а ||b ), для которой требуется построить линию наибольшего наклона к горизонтальной плоскости проекций H.
Проведем в данной плоскости горизонталь h (рис. 68). Прямая n , перпендикулярная к прямой h , перпендикулярна и к следу плоскости H (KL ^H) (рис. 69).

Угол наклона прямой n к плоскости H определяется как угол между прямой и ее проекцией на плоскость H. Строим KK ¢^H (рис. 69). Тогда угол j — искомый угол наклона прямой n к плоскости H.

На рис. 68 построена линия наибольшего наклона плоскости к горизонтальной плоскости проекций — прямая n . Угол наклона плоскости к плоскости H получают при определении натуральной величины отрезка KM при построении прямоугольного треугольника по проекциям K ¢M ' и .

3 Прямая, перпендикулярная к плоскости
Прямая, перпендикулярная к плоскости, если перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости. На основании теоремы о проецировании прямого угла в качестве прямых плоскости общего положения удобнее всего использовать ее линии уровня.
Поэтому, проводя перпендикуляр к плоскости, необходимо брать в этой плоскости две такие прямые: горизонталь и фронталь.
Проекции прямой, перпендикулярной к плоскости, на комплексном чертеже перпендикулярны к соответствующим проекциям ее линий уровня, т.е. если прямая линия перпендикулярна плоскости, то ее горизонтальная проекция должна быть перпендикулярна горизонтальной проекции горизонтали, а ее фронтальная проекция — фронтальной проекции фронтали (рис. 70) или соответствующим следам плоскости (рис. 71).
 |  |
| Рис. 70 | Рис. 71 |
На рис. 72 изображена плоскость общего положения (a ||b ), к которой к которой требуется провести перпендикулярную прямую.

Проводим в данной плоскости горизонталь h (через точки 1,3) и фронталь v (через точки 1,4) (рис. 72).
Затем из точки 1 проводим прямую n перпендикулярно к горизонтали и фронтали плоскости следующим образом:
n ¢^h ¢; n ²^h ².
Построенная прямая n (n' , n'' ) является искомым перпендикуляром к плоскости .
4. Перпендикулярные плоскости
Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную данной плоскости. Построение таких плоскостей может быть выполнено двумя путями:
1) плоскость проводится через перпендикуляр к другой;
2) плоскость проводится перпендикулярно прямой, принадлежащей другой плоскости.
На рис. 73 изображены прямая общего положения и плоскость общего положения (а ´b ). Требуется построить через прямую плоскость, перпендикулярную к плоскости .

Для решения задачи необходимо через какую-нибудь точку данной прямой, например, точку М, провести перпендикуляр к плоскости , заданной пересекающимися прямыми a и b.
Проводим в плоскости горизонталь h и фронталь v (рис. 73).

Далее из точки М , взятой на прямой , опускаем перпендикуляр n , пользуясь рассмотренным выше положением: n' ^h' ; n'' ^v'' , т.е. горизонтальная проекция перпендикуляра будет перпендикулярна горизонтальной проекции горизонтали, а фронтальная его проекция — перпендикулярна фронтальной проекции фронтали (рис. 73).

Плоскость (Çn ), проходящая через прямую n , будет перпендикулярна к плоскости .
6.5 Перпендикулярные прямые
Две прямые перпендикулярны в том и только в том случае, если через каждую из них можно провести плоскость, перпендикулярную к другой прямой.

На рис. 74 изображена прямая общего положения, к которой требуется провести перпендикулярную прямую.


Через точку А прямой строим перпендикулярную к ней плоскость (h Çv ) (рис. 71):
' ^h ' ; '' ^h '' .

Любая прямая, лежащая в плоскости будет также перпендикулярна к данной прямой . Поэтому проведем в этой плоскости произвольную прямую t , на которой возьмем произвольную точку, например, точку В (рис. 74).

Соединив точки А и В , лежащие в плоскости, получим прямую n , перпендикулярную к данной прямой (рис. 74).
I. Роль и место данной темы в школьном курсе, цели ее изучения.
II. Содержание материала.
III.Некоторые методические рекомендации по изучению материала о параллельности и перпендикулярности прямых и плоскостей.
I. Изучение параллельности и перпендикулярности прямых и плоскостей в курсе стереометрии может осуществляться в различной последовательности (сначала перпендикулярность, а затем параллельность и наоборот).
В настоящее время их изучение в школе начинается с аффинной ее части – с параллельности. Это дает возможность пораньше познакомить учащихся с изображением пространственных фигур на плоскости, позволяет показать роль аксиом при изложении этого раздела, развивать конструктивные навыки учащихся в процессе решения позиционных задач. Тема играет важную роль в процессе формирования пространственных представлений учащихся, обобщаются известные из планиметрии сведения о параллельности и перпендикулярности прямых. Основная цель изучения – дать учащимся систематические знания о параллельности и перпендикулярности прямых и плоскостей в пространстве.
1) параллельность прямых в пространстве;
2) параллельность прямой и плоскости;
3) параллельность плоскостей в пространстве;
4) параллельная проекция и ее свойства. Изображение пространственных фигур на плоскости.
Для новых трех блоков можно выделить общий план изучения:
3) вопрос существования и единственности;
4) свойства (для параллельных плоскостей).
1) перпендикулярность прямых в пространстве;
2) перпендикулярность прямой и плоскости;
3) перпендикулярность плоскостей.
1) перпендикулярность прямых;
2) перпендикулярность прямой и плоскости, признак перпендикулярности прямой и плоскости; перпендикуляр, наклонная, проекция наклонной на плоскость; расстояние точки до плоскости, теоремы о параллельности и перпендикулярности прямой и плоскости;
3) перпендикулярность плоскостей; теоремы о параллельности и перпендикулярности плоскостей; расстояние от прямой до параллельной ей плоскости; расстояние между параллельными плоскостями.
2. При изучении понятий данной темы можно придерживаться следующей методологической схемы:
1) формулировка определения учителем;
3) логический анализ формулировки определения;
4) упражнения на распознавание понятия; приведение примеров из окружающей обстановки с соответствующим обоснованием.
3. При изучении теорем, выражающих признаки параллельности или перпендикулярности прямых и плоскостей, целесообразно придерживаться такой методической схемы:
1) мотивация изучения признака;
2) раскрытие содержания теоремы на стереометрическом ящике, на реальных объектах;
3) формулировка признака;
5) оформление доказательства в соответствии с принятыми требованиями;
6) показ применимости признака на простейшей модели;
7) закрепление при решении задач.
4. Остановимся на роли задач при изучении вопросов параллельности и перпендикулярности в пространстве.
Сначала, как известно, вводится – определяется перпендикулярность (параллельность), затем рассматривается вопрос о существовании такого расположения, тесно связанный с признаками перпендикулярности (параллельности) и конструктивными задачи, т.е. воображаемыми построениями перпендикулярных (параллельных) прямых и плоскостей. Эти построения весьма разнообразны.
Вопросы для самопроверки.
1. Какова основная цель изучения параллельности и перпендикулярности прямых и плоскостей в курсе стереометрии?
2. Какие блоки можно выделить в материале о параллельности прямых и плоскостей в пространстве, перпендикулярности прямых и плоскостей.
3. Какую методическую схему изучения понятий этой темы можно использовать?
4. Какую методическую схему можно предложить для изучения теорем, выражающих признаки параллельности (перпендикулярности) прямых и плоскостей?

В этом видеоуроке мы скажем, какие прямые называются перпендикулярными. Поговорим о свойствах перпендикулярных прямых. Скажем, какие прямые называются параллельными. Научимся строить параллельные и перпендикулярные прямые.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности



Конспект урока "Параллельность и перпендикулярность"

На одном из предыдущих занятий мы с вами рассматривали простейшие геометрические фигуры, в том числе и углы. И среди всех углов выделили прямой угол, равный . Сейчас снова вернёмся к нему. Изобразим прямой угол и продолжим его стороны за вершину. Мы получили две прямые, которые пересекаются под прямым углом.

Две прямые, пересекающиеся под прямым углом, называются перпендикулярными.
Обозначают перпендикулярные прямые вот так: , .

Проверить, являются ли прямые перпендикулярными, мы можем, конечно же, с помощью транспортира. Для этого мы совместим точку пересечения прямых с серединой транспортира и расположим транспортир так, чтобы одна из его сторон прошла по линейке. Тогда если вторая прямая проходит через штрих , то данные прямые пересекаются под прямым углом. А значит, эти прямые перпендикулярны.

Проверить, перпендикулярны прямые или нет, можно также с помощью чертёжного угольника. Для этого нам надо совместить точку пересечения прямых с вершиной прямого угла угольника и расположить его так, чтобы одна из прямых совпала со стороной прямого угла угольника. При этом если вторая прямая совпадёт со второй стороной прямого угла угольника, то значит, прямые пересекаются под прямым углом. Следовательно, данные прямые перпендикулярны.

При этом обратите внимание, что совсем необязательно измерять все четыре угла. Если один угол прямой, то и остальные три тоже будут прямыми.
Строители иногда проверяют перпендикулярность стены основанию дома с помощью отвеса, который представляет собой грузик, подвешенный на тонкой гибкой нити.

Построить перпендикулярные прямые можно с помощью транспортира или чертёжного угольника.
Давайте построим перпендикулярные прямые с помощью транспортира. Проведём произвольную прямую . Приложим к этой прямой транспортир так, чтобы она прошла по линейке. Найдём на шкале штрих, который соответствует . И проведём через него прямую , которая и будет перпендикулярна прямой .

Теперь построим перпендикулярные прямые с помощью угольника. Проведём прямую . Возьмём угольник и совместим сторону его прямого угла с этой прямой. Затем вдоль второй стороны прямого угла угольника проведём прямую . Таким образом, мы построили перпендикулярные прямые и .

Теперь поговорим о свойствах перпендикулярных прямых.
Итак, через точку вне данной прямой можно провести только одну прямую, перпендикулярную этой прямой и пересекающую её.
Так, например, через точку А, которая не лежит на прямой , можно провести единственную прямую, перпендикулярную данной прямой . Остальные прямые, проходящие через точку А и пересекающие прямую , являются наклонными прямыми.

Если точка А будет лежать на прямой ? В этом случае одна из прямых, проходящих через точку А и перпендикулярных прямой , будет лежать в плоскости тетради, а все остальные (их бесконечное число) будут прокалывать лист в данной точке. Они будут находиться вне плоскости листа, то есть в пространстве.

Это напоминает дорожный столб, который стоит на перекрёстке дорог. Он перпендикулярен каждой дороге.

Свойство. Если взять точку на самой прямой, то через эту точку проходит бесконечное число прямых, перпендикулярных данной прямой.
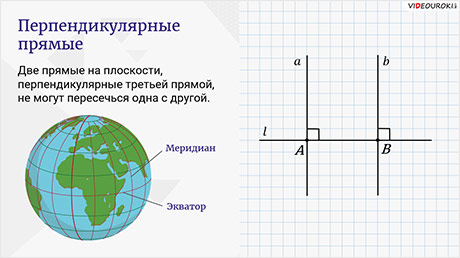
И ещё одно свойство. Две прямые на плоскости, перпендикулярные третьей прямой, не могут пересечься одна с другой.
Пусть прямая перпендикулярна прямой и пересекает её в точке А. Прямая перпендикулярна прямой и пересекает её в точке B. Тогда, если бы прямые и пересеклись, например, в точке C, мы получили бы треугольник ABC, у которого два прямых угла. А это же невозможно.

Поэтому на плоскости такого быть не может. А вот, например, на сфере по-другому. Вспомним экватор и меридианы. Они перпендикулярны друг другу, но при этом все меридианы пересекаются в одной точке – на полюсе.

Поговорим о прямых, которые не пересекаются на плоскости.

Пусть на плоскости дана прямая и некоторая точка К, которая не лежит на этой прямой. Проведём через точку К несколько прямых.


Все эти прямые, кроме одной, пересекают прямую .
Запомните! Две прямые на плоскости называются параллельными, если они не пересекаются.
Без труда построить параллельные прямые мы можем с помощью чертёжного угольника и линейки.
Давайте проведём прямую, параллельную прямой , через точку М. Для этого мы совместим сторону прямого угла угольника с прямой . К другой стороне прямого угла угольника приложим линейку. Теперь будем двигать наш угольник вдоль линейки до тех пор, пока точка М не окажется на стороне прямого угла угольника. Затем проведём прямую . Прямые и параллельны.

Представление о параллельных прямых мы можем получить, посмотрев на железнодорожные рельсы или на электрические провода.
Так, мы с вами познакомились с перпендикулярными и параллельными прямыми. А также научились их строить с помощью транспортира или угольника. Строить параллельные и перпендикулярные прямые можно также с помощью циркуля и линейки.
Проведём параллельные прямые. Итак, пусть проведена прямая и отмечена точка А вне этой прямой. Проведём через точку А произвольную окружность, которая пересекает прямую .
Одну из точек пересечения окружности с прямой обозначим буквой B, вторую – обозначим B1. Измерим циркулем отрезок АB и проведём окружность радиусом, равным отрезку АB, с центром в точке B1. Появится точка A1. Проведём через точки А и A1 прямую . Прямая параллельна прямой .

Теперь проведём перпендикуляр к прямой. Пусть проведена прямая и дана точка А, которая не лежит на этой прямой. Отметим на прямой две произвольные точки. И с помощью циркуля проведём через точку А две произвольные окружности с центрами в этих точках.
Первая точка пересечения этих окружностей – это точка А. Вторую точку A1. Проведём через эти точки прямую . Это и есть перпендикуляр к прямой .

Давайте рассмотрим одно свойство перпендикулярных прямых. Пусть даны перпендикулярные прямые и . Если А – точка на прямой , а B – точка пересечения перпендикулярных прямых и , то отрезок АB есть кратчайшее расстояние от точки А до прямой .

Получается, если мы хотим из точки А по кратчайшему пути попасть на прямую , то двигаться надо по перпендикуляру к прямой .
Посмотрите на следующие рисунки. На них изображены перпендикулярные и , и . На этих прямых лежат отрезки. Отрезки, лежащие на перпендикулярных прямых, также называются перпендикулярными. Получается, что , а .

То же самое мы можем сказать и про отрезки, которые лежат на параллельных прямых. Отрезки, лежащие на параллельных прямых, также называются параллельными. Так, например, отрезки и , которые лежат на параллельных прямых и , также являются параллельными.

Теперь посмотрим на куб. Среди его рёбер можно указать пары параллельных и перпендикулярных рёбер.


Через рёбра и можно провести плоскость . Эту плоскость называют диагональным сечением куба.
А вот если мы посмотрим на пару рёбер и . Они не пересекаются, но при этом мы не сможем назвать ни одной плоскости, которая бы проходила через оба эти отрезка (либо через прямые и ).
Запомните! Прямые, которые не пересекаются, но не лежат в одной плоскости, называются скрещивающимися.
Читайте также:
- Поверхностное пластическое деформирование реферат
- Особенности обеспечения безопасных условий труда в сфере физической культуры и спорта реферат
- Қарахан кесенесі реферат қазақша
- Реферат по географии 8 класс на тему природа арктических островов
- 1 сущность ценностный характер социально экологического образования школьников реферат

