Обработка результатов совместных измерений на основе метода наименьших квадратов реферат

Обновлено: 02.07.2024

При совместных и совокупных измерениях значения искомых величин или параметров находят посредством решения систем уравнений. Эти уравнения наряду с упомянутыми параметрами содержат также величины, значения которых можно определить при помощи прямых или косвенных измерений. Характер зависимости, связывающей все эти величины, предполагается известным. Пусть, например, указанная зависимость имеет вид

В этой формуле подлежат определению величины a₁ , a₂, . ,a_j , . , a_m , которые недоступны непосредственному наблюдению, в то время как значения y и x₁ , x₂ , . , x_k , . , x_t могут быть измерены прямым или косвенным методом. Предположим, что произведено m измерений величины y при m различных значениях каждой из величин x₁ , x₂ , . , x_k , . , x_t . Это дает возможность составить систему уравнений

решением которой являются оценки искомых величин . Из-за того, что значения y_i и x_1i , x_2i , . , x_ki , . , x_ti получены в результате измерений, они содержат погрешности. Следовательно оценки тоже не свободны от погрешностей. Для увеличения точности приходится увеличивать число измерений, то есть производить вместо m n измерений, где n > m. Однако это приводит к несовместности системы уравнений (3.66). Вследствие случайных погрешностей при любых значениях a₁ , a₂, . ,a_j , . , a_m уравнение (3.65) не выполняется, поэтому

Каждое значение D_i ( i = 1, . , n) в общем случае не равно нулю. Чтобы найти значения коэффициентов a₁ , a₂, . ,a_j , . , a_m следует обратиться к методу наименьших квадратов. Этот метод был разработан Лежандром и Гауссом в начале 19-го столетия. Согласно ему наилучшими считаются оценки параметров а_j ( j = 1,2. m ) , при которых сумма квадратов D_i минимальна:

S = = min. (3.68)

Для простоты будем считать, что параметры а_i входят в f линейно, т.е. уравнение (2.59) сводится к виду:

S= 2 (3.70)

и условие минимума S дает систему m уравнений

x_ji=0, (3.71)

решение которых относительно параметров приводит к нахождению искомых оценок .

На практике стараются организовать измерения таким образом, чтобы число параметров было как можно меньше. В этих случаях результат решения системы (3.71) имеет обозримый и достаточно простой вид. В противном случае приходится прибегать к матричному исчислению и вычислять определители большой размерности. Впрочем, использование компьютеров существенно упрощает эту задачу.

Погрешности найденных значений параметров также могут быть определены в рамках метода наименьших квадратов.

Метод наименьших квадратов, происходит от английского – Ordinary Least Squares – математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных.
Можно выделить следующие достоинства метода:
а) расчеты сводятся к механической процедуре нахождения коэффициентов;
б) доступность полученных математических выводов.
Основным недостатком метода наименьших квадратов является чувствительность оценок к резким выбросам, которые встречаются в исходных данных.

Файлы: 1 файл

Конспект на тему Метод наименьших квадратов по дисциплине Эконометрика Соболева О.А., гр. 312.docx

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Метод наименьших квадратов, происходит от английского – Ordinary Least Squares – математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов некоторых функций от искомых переменных. Он может использоваться для решения переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функцией. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

Можно выделить следующие достоинства метода:

расчеты сводятся к механической процедуре нахождения коэффициентов;
доступность полученных математических выводов.

Основным недостатком метода наименьших квадратов является чувствительность оценок к резким выбросам, которые встречаются в исходных данных.

Рассмотри сущность применение классического метода наименьших квадратов. Пусть дана система уравнений f_i(x)= y_i, i=1…n где:

f_i – некоторые функции;

y_i – некоторые известные значения;

x – набор неизвестных (искомых) переменных.

Для произвольных значений x значения y_i отличаются от f_i(x).

Суть метода наименьших квадратов заключается в том, чтобы найти такие значения x, при которых минимизируется сумма квадратов отклонений (ошибок) e_i= y_{i –} f_i(x):

Используя оператор псевдоинверсии, решение можно переписать так:

x=A + b, где A + - псевдообратная матрица для A.

Рассмотрим аппроксимацию данны х и метод наименьших квадратов.

Аппроксимация это приближенное выражение каких–либо математических объектов, чисел или функций, через другие более простые. В научных исследованиях аппроксимация применяется для описания, анализа, обобщения и дальнейшего использования эмпирических результатов. Как известно, между величинами может существовать точная функциональная связь, когда одному значению аргумента соответствует одно определенное значение, и менее точная корреляционная связь, когда одному конкретному значению аргумента соответствует приближенное значение или некоторое множество значений функции, в той или иной степени близких друг к другу. При выборе аппроксимации следует исходить из конкретной задачи исследования. Обычно, чем более простое уравнение используется для аппроксимации, тем более приблизительно получаемое описание зависимости.

В регрессионном анализе и в частности в эконометрике используются вероятностные модели зависимости между переменными

где – так называемые случайные ошибки модели.

Соответственно, отклонения наблюдаемых значений y от модельных f(x,b) предполагается уже в самой модели. Сущность обычного, классического метода наименьших квадратов заключается в том, чтобы найти такие параметры b, при которых сумма квадратов отклонений (ошибок, для регрессионных моделей их часто называют остатками регрессии) будет минимальной: ,

где RSS – происходит от английского Residual Sum of Squares и определяется как:

В общем случае решение этой задачи может осуществляться численными методами оптимизации (минимизации). В этом случае говорят о нелинейном методе наименьших квадратов (NLLS происходит от английского Non–Linear Least Squares). Во многих случаях можно получить аналитическое решение. Для решения задачи минимизации необходимо найти стационарные точки функции RSS(b), продифференцировав её по неизвестным параметрам b, приравняв производные к нулю и решив полученную систему уравнений:

Метод наименьших квадратов широко применяется для построения регрессионных моделей при обработке экспериментальных данных. Наиболее распространенным является случай линейной регрессии.

Пусть регрессионная зависимость является линейной:

Пусть y векторстолбец наблюдений объясняемой переменной, x это матрица наблюдений факторов (строки матрицы векторы значений факторов в данном наблюдении, по столбцам вектор значений данного фактора во всех наблюдениях). Матричное представление линейной модели имеет вид:

Тогда вектор оценок объясняемой переменной и вектор остатков регрессии будут равны

соответственно сумма квадратов остатков регрессии будет равна

Дифференцируя эту функцию по вектору параметров b и приравняв производные к нулю, получим систему уравнений (в матричной форме):

В расшифрованной матричной форме эта система уравнений выглядит следующим образом:

где все суммы берутся по всем допустимым значениям t.

Если в модель включена константа, то при всех t, поэтому в левом верхнем углу матрицы системы уравнений находится количество наблюдений n, а в остальных элементах первой строки и первого столбца – просто суммы значений переменных: и первый элемент правой части системы – .

Решение этой системы уравнений и дает общую формулу метода наименьших квадратов – оценок для линейной модели:

Для аналитических целей оказывается полезным последнее представление этой формулы в системе уравнений при делении на n, вместо сумм фигурируют средние арифметические. Если в регрессионной модели данные центрированы, то в этом представлении первая матрица имеет смысл выборочной ковариационной матрицы факторов, а вторая – вектор ковариаций факторов с зависимой переменной. Если кроме того данные ещё и нормированы на средне квадратичное отклонение (то есть в конечном итоге стандартизированы), то первая матрица имеет смысл выборочной корреляционной матрицы факторов, второй вектор – вектора выборочных корреляций факторов с зависимой переменной.

Немаловажное свойство метода наименьших квадратов – оценок для моделей с константой – линия построенной регрессии проходит через центр тяжести выборочных данных, то есть выполняется равенство:

В частности, в крайнем случае, когда единственным регрессором является константа, получаем, что метод наименьших квадратов – оценка единственного параметра (собственно константы) равна среднему значению объясняемой переменной. То есть среднее арифметическое, известное своими хорошими свойствами из законов больших чисел, также является метод наименьших квадратов – оценкой удовлетворяет критерию минимума суммы квадратов отклонений от неё.

В случае парной линейной регрессии , когда оценивается линейная зависимость одной переменной от другой, формулы расчета упрощаются (можно обойтись без матричной алгебры). Система уравнений имеет вид:

Отсюда несложно найти оценки коэффициентов:

Несмотря на то, что в общем случае модели с константой предпочтительней, в некоторых случаях из теоретических соображений известно, что константа a должна быть равна нулю. Например, в физике зависимость между напряжением и силой тока имеет вид U=I R; замеряя напряжение и силу тока, необходимо оценить сопротивление. В таком случае речь идёт о модели y=bx. В этом случае вместо системы уравнений имеем единственное уравнение

следовательно, формула оценки единственного коэффициента имеет вид:

Статистические свойства метода наименьших квадратов - оценок

В первую очередь, отметим, что для линейных моделей метода наименьших квадратов – оценки являются линейными оценками, как это следует из вышеприведённой формулы. Для несмещенности метода наименьших квадратов – оценок необходимо и достаточно выполнения важнейшего условия регрессионного анализа: условное по факторам математическое ожидание случайной ошибки должно быть равно нулю. Данное условие, в частности, выполнено, если:

математическое ожидание случайных ошибок равно нулю, и
факторы и случайные ошибки – независимые случайные величины.

Первое условие можно считать выполненным всегда для моделей с константой. Константа – величина, значение которой не меняется, в этом она противоположна переменной. Константа берёт на себя ненулевое математическое ожидание ошибок (поэтому модели с константой в общем случае предпочтительнее).

Если это свойство не выполнено, то можно считать, что практически любые оценки будут крайне неудовлетворительными: они не будут даже состоятельными (то есть даже очень большой объём данных не позволяет получить качественные оценки в этом случае). В классическом случае делается более сильное предположение о детерминированности факторов, в отличие от случайной ошибки, что автоматически означает выполнение условия экзогенности. В общем случае для состоятельности оценок достаточно выполнения условия экзогенности вместе со сходимостью матрицы V_x к некоторой невырожденной матрице при увеличении объёма выборки до бесконечности.

Для того, чтобы кроме состоятельности и несмещенности, оценки (обычного) метода наименьших квадратов были ещё и эффективными (наилучшими в классе линейных несмещенных оценок) необходимо выполнение дополнительных свойств случайной ошибки:

на тему: Метод наименьших квадратов как применение теорем поиска экстремума функций многих переменных

Автор работы А.М.Филимонова Группа ББИ-21

Обозначение курсовой работы ТГТУ.080500.018 ДЭ

Руководитель работы А.Н.Пчелинцев

подпись, дата инициалы, фамилия

Тамбов 2014 г.

ЗАДАНИЕ

на курсовую работу

Студент А.М.Филимонова код 018 Группа ББИ-21

1 Тема: Метод наименьших квадратов как применение теорем поиска экстремума функций многих переменных

2 Срок представления работы к защите

3 Исходные данные для проектирования (научного исследования)

Учебная литература по теме работы

4 Перечень разделов пояснительной записки

4.2 Метод наименьших квадратов

4.3 Линейная парная регрессия и её коэффициенты

4.4 Применение МНК

4.6 Список используемых источников

5 Перечень графического материала:

Таблица 1 – Статистические данные в общем виде

Таблица 2 – Выборка из экономических показателей

Таблица 3 – Упорядоченная выборка

Таблица 4 – Расчётная таблица выборки

Рисунок 1 – График, изображающий прямую регрессии и точки отклонений

Рисунок 2 – График найденной регрессии

А.Н.Пчелинцев подпись, дата инициалы, фамилия

Задание принял к исполнению

подпись, дата инициалы, фамилия

Метод наименьших квадратов…………………………………………..

История появления метода наименьших квадратов…………………..

Понятие и определение метода наименьших квадратов………………

Линейная парная регрессия и её коэффициенты………………………

Понятие линейной парной регрессии…………………………………..

Вывод формул для нахождения коэффициентов регрессии………….

2.3 Проверка достаточного условия экстремума (минимума) функции.

3.1 Пример использования МНК для линейной парной регрессии ……..

3.2 Области применения МНК………………………………………………. 21

Список используемых источников…………………………………………. 25

Метод наименьших квадратов имеет большое применение во многих областях, так как это один из методов оценки величин по результатам измерений, содержащим случайные ошибки. Он часто оказывается полезным при обработке наблюдений.

Также, метод наименьших квадратов используется как составная часть некоторой более общей проблемы. Например, при необходимости проведения аппроксимации наиболее часто употребляется именно метод наименьших квадратов. На этом подходе основаны: регрессионный анализ в статистике, оценивание параметров в технике и т.д.

Цель моей курсовой работы – рассмотреть метод наименьших квадратов как применение теорем поиска экстремума функций многих переменных.

Исходя из поставленной цели, необходимо решить следующие задачи:

- рассмотреть метод наименьших квадратов, линейную парную регрессию;

- вывести формулы для нахождения коэффициентов линейной парной регрессии;

- доказать, что найденная функция принимает минимальное значение, если коэффициенты являются решениями системы.

1 МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

1.1 История появления метода наименьших квадратов

До начала XIX в. учёные не имели определённых правил для решения системы уравнений, в которой число неизвестных меньше, чем число уравнений; до этого времени употреблялись частные приёмы, зависевшие от вида уравнений и от остроумия вычислителей, и потому разные вычислители, исходя из тех же данных наблюдений, приходили к различным выводам. Гауссу (1795) принадлежит первое применение метода, а Лежандр (1805) независимо открыл и опубликовал его под современным названием (фр. Méthode des moindres quarrés). Лаплас связал метод с теорией вероятностей, а американский математик Эдрейн (1808) рассмотрел его теоретико-вероятностные приложения.

Метод распространён и усовершенствован дальнейшими изысканиями Энке, Бесселя, Ганзена и других. Как и в случае арифметической середины, вновь изобретённый способ не даёт, конечно, истинных значений искомых, но зато даёт наиболее вероятные значения. Он получил название метода наименьших квадратов, потому что после подстановки в начальные уравнения неизвестных величин, выведенных этим способом, в правых частях уравнений получаются если и не нули, то небольшие величины, сумма квадратов которых оказывается меньшей, чем сумма квадратов подобных же остатков после подстановки каких бы то ни было других значений неизвестных. Решение уравнений по способу наименьших квадратов даёт возможность выводить вероятные ошибки неизвестных, то есть величины, по которым судят о степени точности выводов.

1.2 Понятие и определение метода наименьших квадратов

Метод наименьших квадратов — один из методов регрессионного анализа, использующийся для нахождения оценок параметров регрессии ,основанный на минимизации суммы квадратов всех остатков.

Регрессионный (линейный) анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2. Xp. Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных, а не причинно-следственные отношения.

Когда искомая величина может быть измерена непосредственно, как, например, длина отрезка или угол, то, для увеличения точности, измерение производится много раз, и за окончательный результат берут арифметическое среднее из всех отдельных измерений. Это правило арифметической середины основывается на соображениях теории вероятностей; легко показать, что сумма квадратов уклонений отдельных измерений от арифметической середины будет меньше, чем сумма квадратов уклонений отдельных измерений от какой бы то ни было другой величины. Само правило арифметической середины представляет, следовательно, простейший случай метода наименьших квадратов.

Основная идея данного метода состоит в том, что в качестве критерия точности решения задачи рассматривается сумма квадратов ошибок, которую стремятся свести к минимуму. При использовании этого метода можно применять как численный, так и аналитический подход.

В частности, в качестве численной реализации метод наименьших квадратов подразумевает проведение как можно большего числа измерений неизвестной случайной величины. Причем, чем больше вычислений, тем точнее будет решение. На этом множестве вычислений (исходных данных) получают другое множество предполагаемых решений, из которого затем выбирается наилучшее. Если множество решений параметризировать, то метод наименьших квадратов сведется к поиску оптимального значения параметров.

В качестве аналитического подхода к реализации МНК на множестве исходных данных (измерений) и предполагаемом множестве решений определяется некоторая функциональная зависимость (функционал), которую можно выразить формулой, получаемой в качестве некоторой гипотезы, требующей подтверждения. В этом случае метод наименьших квадратов сводится к нахождению минимума этого функционала на множестве квадратов ошибок исходных данных.

Зачастую отклонения измерений от точного значения бывают как положительными, так и отрицательными. При определении средней погрешности измерений простое суммирование может привести к неверному выводу о качестве оценки, поскольку взаимное уничтожение положительных и отрицательных значений понизит мощность выборки множества измерений. А, следовательно, и точность оценки. Для того чтобы этого не произошло, и суммируют квадраты отклонений. Даже более того, чтобы выровнять размерность измеряемой величины и итоговой оценки, из суммы квадратов погрешностей извлекают квадратный корень.

Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений. Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

2 ЛИНЕЙНАЯ ПАРНАЯ РЕГРЕССИЯ И ЕЁ КОЭФФИЦИЕНТЫ

2.1 Понятие линейной парной регрессии

Регрессией в теории вероятностей и математической статистике принято

называть зависимость среднего значения какой-либо величины (y) от некоторой

Парной регрессией называется модель, выражающая зависимость средне-

го значения зависимой переменной y от одной независимой переменной х

где ŷ – зависимая переменная (результативный признак); х – независимая,

объясняющая переменная (признак–фактор).

Парная регрессия применяется, если имеется доминирующий фактор, обуславливающий большую долю изменения изучаемой объясняемой переменной,который и используется в качестве объясняющей переменной.

Множественной регрессией называют модель, выражающую зависимость

среднего значения зависимой переменной y от нескольких независимых пере-

менных х1, х2, …, хp

ŷ = f (х1, х2, …, хp) (2)

Множественная регрессия применяется в ситуациях, когда из множества

факторов, влияющих на результативный признак, нельзя выделить один доми-

нирующий фактор и необходимо учитывать одновременное влияние несколь-

Используя уравнение регрессии (1), соотношение между значениями пе-

ременными у и х (модель связи) можно записать как

где первое слагаемое f(x) можно интерпретировать как ту часть значения y, ко-торая объяснена уравнением регрессии (1), а второе слагаемое ε как необъяс-ненную часть значения y (или возмущение). Соотношение между этими частя-

ми характеризует качество уравнения регрессии, его способность представлять

зависимость между переменными х и y. При построении уравнения регрессии ε

рассматривается как ошибка модели, представляющая собой случайную вели-

чину, удовлетворяющую определенным предположениям.

Наличие составляющей ε обусловлено такими причинами, как наличие дополнительных факторов, оказывающих влияние на переменную y, неверный

вид функциональной зависимости f(x), ошибки измерения, выборочный харак-

тер исходных данных.

По виду аналитической зависимости различают линейные и нелинейные

Линейная парная регрессия описывается уравнением:

Итак, эта функция (4), описывающая изменение условного математического ожидания случайной переменной y при изменении значений х, называется функцией регрессии, а ее график – линией регрессии.

2.2 Вывод формул для нахождения коэффициентов регрессии

Пусть случайно выбранные исходные данные записаны в таблицу для упрощения дальнейших расчётов (таблица 1).

2) оценить вид закона распределения случайной погрешности.

Обработка совместных измерений

В ходе исследований часто прибегают к совместным измерениям, целью которых является установления функции вида – математическая модель исследуемой зависимости. Из-за погрешности измерений и неполноты модели экспериментальные точки имеют определённый разброс, поэтому точно определить модель невозможно, и ограничиваются нахождением её оценки . Оценка должна удовлетворять двум противоречивым требованиям: обеспечить сглаживание случайных отклонений экспериментальных точек и при этом отражать все особенности полученной зависимости.

Экспресс-методы определения графического вида математической модели

Математическую модель можно грубо оценить по экспериментальной шкале, не прибегая к вычислениям.

· Если рассеивание точек невелико, то их просто соединяют плавной кривой. Выпадающие из общей зависимости точки рассматривают как проявление промахов и не учитывают.

· При значительных погрешностях применяют метод контура– проводят линии, ограничивающие поле экспериментальных точек сверху и снизу. График искомой математической модели строят как центральную линию полученного контура (рис. 4.1).

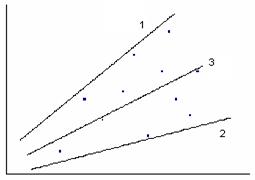
Рис. 4.1

При больших погрешностях и часто встречающихся промахах из-за возрастания неопределённости при построении контура становится мало эффективным. В таких случаях можно использовать метод медианных центров, основанный на устойчивых к промахам медианных оценках среднего значения.

Всё поле экспериментальных точек делят на несколько областей.

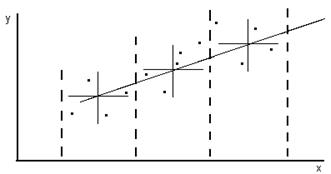
Рис. 4.2

На рис. 4.2 выделены три области, ограниченные штриховыми линиями. В каждой области находят медианный центр. Для этого проводят горизонтальную линию, выше нижи которой число точек одинаково (по две точки в каждой области), а затем вертикальную линию, справа и слева от которой число точек также одинаково. Медианные центры, лежащие на пересечении линий, соединяют плавной линией.

Медианные центры можно использовать для исключений промахов. Например, при монотонно изменяющихся отсчетов вместо очередного отсчёта берут медиану трёх соседних отсчетов.

Выбор математической модели

Вид зависимости , описывающей опытные данные, выбирает экспериментатор на основе предварительных данных о природе исследуемой зависимости или о расположении эксперимента. Крайне желательно чтобы модель была содержательной, т.е. чтобы входящим в неё постоянным можно было приписать определённый физический смысл. Задача выбора математической модели решается в два этапа:

1. находят общий вид модели;

2. рассчитывают параметры модели, определяют её конкретный вид.

Если нельзя указать общий вид модели теоретически, то её определяют по форме поля рассеивания экспериментальных точек. Для этого в поле рассеивания помещают графики различных известных функций и находят такие, которые отражают особенности этого поля. Такой выбор неоднозначен, т.к. обычно можно найти несколько подходящих функций.

В некоторых случаях подбор математической модели упрощается, если масштабы по осям и выбрать так, что график аппроксимирующей функции превратится в прямую линию.

Пример:

Графическое изображение в координатах , является прямой линией с угловым коэффициентом n. По графику можно грубо оценить параметры модели. Для этого проводят линию, берут на ней две точки с координатами и и рассчитывают угловой коэффициент и параметр a:

2) - график показательной функции превращается в прямую линию, если выбрать масштаб: можно приближено оценить параметры a и b.

Применяя функциональные шкалы, можно использовать рассмотренный метод.

Метод наименьших квадратов

После того как установлен вид математической модели, аналитическими методами рассчитывают её параметры. Наиболее распространен метод наименьших квадратов.

Сущность метода состоит в таком выборе параметров модели, при которых сумма квадратов отклонений минимальна.

Если систематическая погрешность измерений значений отсутствует, случайная погрешность подчинена гауссовскому закону с постоянной дисперсией, а погрешности последовательности измерений статистически независимы, то вычисленные с помощью метода наименьших квадратов значения параметров математической модели являются оценками максимального правдоподобия.

При экспериментальной обработке системы двух связанных случайных величин можно пользоваться методом наименьших квадратов. Если предположить, что случайные величины связаны между собой по линейному закону, то метод наименьших квадратов позволяет рассчитать параметры прямой, которая называется линией регрессии.

На практике эти условия выполняются редко, и метод наименьших квадратов является просто удобным аналитическим способом расчета параметров математической модели.

Известно, что прямая линия имеет два параметра. Обозначим их a и b: .

Метод наименьших квадратов позволяет c наилучшей точностью рассчитать коэффициенты А и В.

В итоге получим:

Порядок выполнения работы

Перед началом работы в окне модели установите время моделирования и шаг в соответствии с вариантом (Simulation->Simulation Parameters->Start time=0, Stop time=10, Solver option->Fixed step, Fixed step size=0.1).

Читайте также: