Нейронная сеть кохонена реферат

Обновлено: 07.07.2024

Нейронные сети Кохонена типичный пример нейросетевой архитектуры, обучающейся без учителя. Отсюда и перечень решаемых ими задач: кластеризация данных или прогнозирование свойств. Кроме того, сети Кохонена могут использоваться с целью уменьшения размерности данных с минимальной потерей информации.

Ранее рассмотренные архитектуры нейронных сетей обучались с учителем на выборках данных, включающих множество примеров, состоящих из соответствующих друг другу пар входных и выходных векторов. При этом выходные значения принимали самое непосредственное участие в настройке весовых коэффициентов. В нейронных сетях Кохонена выходные вектора в обучающей выборке могут быть, но могут и отсутствовать, и, в любом случае, они не принимают участия в процессе обучения. То есть выходы не используются в качестве ориентиров при коррекции синапсов. Именно поэтому данный принцип настройки нейронной сети называется самообучением.

В рассматриваемой архитектуре сигнал распространяется от входов к выходам в прямом направлении. Структура нейронной сети содержит единственный слой нейронов (слой Кохонена) без коэффициентов смещения (рис. 1). Общее количество весовых коэффициентов рассчитывается как произведение:

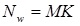
Количество нейронов равно количеству кластеров, среди которых происходит начальное распределение и последующее перераспределение обучающих примеров. Количество входных переменных нейронной сети равно числу признаков, характеризующих объект исследования и на основе которых происходит отнесение его к одному из кластеров.

Следует различать собственно самообучение и самоорганизацию нейронной сети Кохонена. При обычном самообучении сеть имеет строго фиксированную структуру, т. е. количество нейронов, не изменяющееся на протяжении всего жизненного цикла. При самоорганизации сеть, напротив, не имеет постоянной структуры. В зависимости от найденного расстояния до нейрона-победителя либо этот нейрон используется для кластеризации примера, либо для поданного на входы примера создается новый кластер с соответствующими ему весовыми коэффициентами. Кроме того, в процессе самоорганизации структуры сети Кохонена отдельные нейроны могут исключаться из нее.

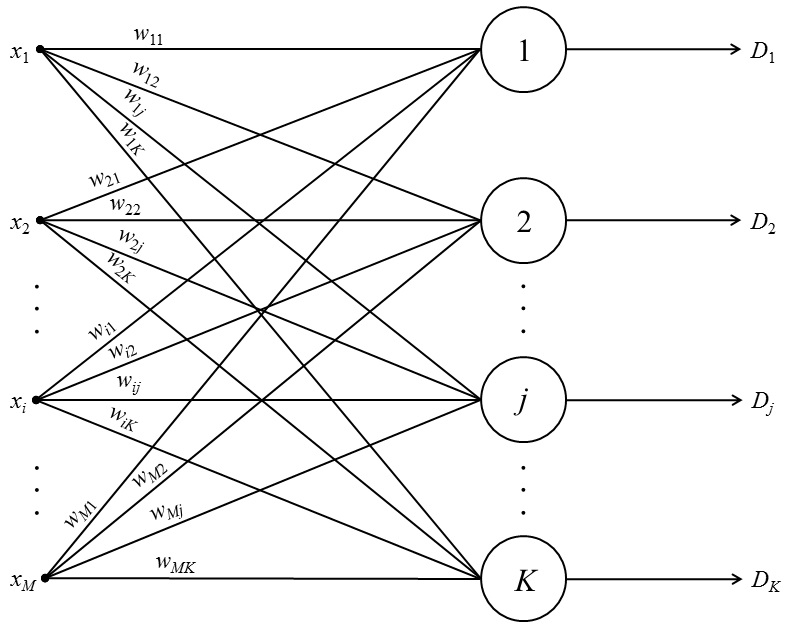
Рис. 1. Общая структура нейронной сети Кохонена

Нормализация входных переменных выполняется в пределах [–1, 1] или [0, 1].

Для жизненного цикла нейронных сетей данной архитектуры характерны три основных стадии жизненного цикла: обучение, кластерный анализ и практическое использование.

Алгоритм обучения сети Кохонена включает этапы, состав которых зависит от типа структуры: постоянной (самообучающаяся сеть) или переменной (самоорганизующаяся сеть). Для самообучения последовательно выполняются:

1. Задание структуры сети (количества нейронов слоя Кохонена) (K).

2. Случайная инициализация весовых коэффициентов значениями, удовлетворяющими одному из следующих ограничений:

– при нормализации исходной выборки в пределах [–1, 1]:

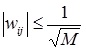
(1)

– при нормализации исходной выборки в пределах [0, 1]:

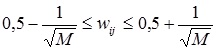
, (2)

где M – количество входных переменных сети – характеристических признаков объекта исследования.

3. Подача на входы сети случайного обучающего примера текущей эпохи обучения и расчет евклидовых расстояний от входного вектора до центров всех кластеров:

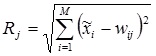
. (3)

4. По наименьшему из значений Rj выбирается нейрон-победитель j, в наибольшей степени близкий по значениям с входным вектором. Для выбранного нейрона (и только для него) выполняется коррекция весовых коэффициентов:

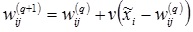
, (4)

где v – коэффициент скорости обучения.

5. Цикл повторяется с шага 3 до выполнения одного или нескольких условий окончания:

– исчерпано заданное предельное количество эпох обучения;

– не произошло значимого изменения весовых коэффициентов в пределах заданной точности на протяжении последней эпохи обучения;

– исчерпано заданное предельное физическое время обучения.

Коэффициент скорости обучения может задаваться постоянным из пределов (0, 1] или переменным значением, постепенно уменьшающимся от эпохи к эпохе.

В случае самоорганизации сети Кохонена алгоритм претерпевает определенные изменения:

1. Задается критическое расстояние R_кр, соответствующее максимально допустимому евклидову расстоянию между входами примера и весами нейрона-победителя. Начальная структура не содержит нейронов. При подаче на входы сети самого первого примера обучающей выборки создается первый нейрон с весовыми коэффициентами, равными поданным входным значениям.

2. На входы сети подается новый случайно выбранный пример текущей эпохи обучения, рассчитываются евклидовы расстояния от примера до центра каждого кластера по соотношению (3) и определяется нейрон-победитель с наименьшим из них R_min.

3. Если выполняется условие R_min R_кр , производится коррекция весовых коэффициентов соответствующего нейрона-победителя по соотношению (4), в противном случае в структуру сети добавляется новый нейрон, весовые коэффициенты которого принимаются численно равными входным значениям поданного примера.

4. Процедура повторяется с п. 2. Если на протяжении последней эпохи обучения какие-либо кластеры остались не задействованными, соответствующие нейроны исключаются из структуры сети Кохонена.

5. Вычисления заканчиваются, если выполняется одно из условий, прописанных в алгоритме самообучения сети фиксированной структуры.

Еще одна модификация алгоритмов самообучения и самоорганизации предусматривает коррекцию весовых коэффициентов не только нейрона-победителя, но и всех остальных нейронов. Для этого следует использовать коэффициент скорости обучения, убывающий с увеличением расстояния до центра кластера R_j:

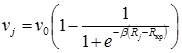
где R_кр – критическое значение расстояния: чем оно меньше, тем более значительны будут корректировки весов самых близких к обучающему примеру кластеров и практически незначимы – весов более-менее удаленных от него; β – параметр, устанавливающий степень нелинейности влияния расстояния на коэффициент скорости; v₀ – базовое (максимально возможное) значение коэффициента скорости на текущей эпохе обучения.

В качестве значения R_кр можно рассчитывать среднее расстояние для каждого кластера при текущем предъявлении обучающего примера. Параметр β рекомендуется выбирать равным 3,0 ± 0,5.

Как правило, на практике при использовании самоорганизации нейронной сети Кохонена приходится сталкиваться еще с одной проблемой. С одной стороны, какие-то кластеры могут содержать слишком маленькое количество примеров, что приводит к сложностям в последующем обобщении информации. С другой стороны, некоторые кластеры могут оказаться слишком большими, то есть содержать очень много примеров. В этом случае для регулирования размера кластера и решения проблемы его переполненности можно задать в качестве дополнительного параметра предельное число примеров, формирующих кластер (N_пр). Если в какой-то момент оказывается, что новый пример должен быть отнесен к кластеру, размер которого уже максимален, принимается решение о создании другого кластера, центр которого будет представлять собой вектор переменных одного из (N_пр + 1) примеров кластера (включая новый) наиболее удаленного от центра данного кластера.

К обученной нейронной сети применяется процедура кластерного анализа – процедуры описания свойств кластера на основе анализа количественного и качественного составов примеров, сформировавших его. Следует учитывать, что описание кластеров может базироваться не только на значениях входных переменных обучающей выборки, но и на значениях переменных, не участвовавших в формировании кластеров. В частности, в описание могут входить данные о средних значениях таких переменных среди всех примеров, сформировавших кластер. Кроме того, целесообразно для каждого кластера иметь данные о среднеквадратическом отклонении или дисперсии по каждой переменной.

При практическом использовании нейронной сети Кохонена новый пример подается на ее вход и относится к одному из существующих кластеров, либо делается вывод о невозможности такого отнесения (при большом расстоянии до центра ближайшего кластера). Если выбор кластера состоялся, его описание, полученное в результате кластерного анализа, и соответствующие кластеру решения должны распространяться в том числе на поданный пример.

Практическое использование сети Кохонена облегчается за счет визуализации результатов кластеризации. В результате самообучения (самоорганизации) сети получается набор кластеров, каждый из которых характеризуется своим центром (значениями весовых коэффициентов соответствующего нейрона) и количеством обучающих примеров, сформировавших его. Не составляет никакого труда определить евклидово расстояние между центрами всех возможных пар кластеров и графически изобразить их на так называемой карте Кохонена – двумерной графической структуре, позволяющей судить не только о размерах и положении каждого отдельно взятого кластера, но и о близости друг к другу и взаимном расположении отдельных кластеров.

Приведем пример самообучения нейронной сети Кохонена для решения задачи кластеризации данных об успеваемости студентов одной из студенческих учебных групп. Исходная выборка представлена в табл. 1.

Всем доброго дня, сегодня мы возвращаемся к интереснейшей теме, а именно к обсуждению нейронных сетей. Вот остальные статьи цикла: ссылка.

А сегодня мы поговорим об еще одном типе сетей под названием сеть Кохонена, которую также называют картой Кохонена. Нам предстоит разобраться, каков принцип ее работы, какие задачи она призвана решать, в общем, нас сегодня интересует все, что касается нейронных сетей данного вида.

Основным их назначением является кластеризация образцов, то есть разделение образцов на группы (кластеры) по тем или иным признакам. Например, может стоять задача классификации спортсменов по виду спорта, которым они занимаются. Тут подходящими признаками могут быть рост, вес, время, за которое спортсмен пробегает стометровку и т. д. Если пропустить "параметры" всех спортсменов через сеть Кохонена, то на выходе мы получим определенное количество групп. При этом должны выполняться следующие условия:

образцы, относящиеся к одной и той же группе должны быть подобны друг другу в некотором смысле
а группы, подобные друг другу, в свою очередь, должны размещаться близко друг к другу

В данном примере все спортсмены, занимающиеся легко атлетикой попадут в одну группу, а баскетболисты в другую. При дальнейшем обучении сети от группы легкоатлетов может отделиться группа бегунов. И тогда, следуя второму из перечисленных свойств, группа бегунов должна располагаться близко к группе легкоатлетов и далеко от группы баскетболистов. Вот так в общих чертах и работают сети данного типа.

Нейронная сеть Кохонена, в отличие от рассмотренных нами ранее сетей, обучается без учителя. И поэтому носит название самоорганизующейся карты Кохонена (SOFM - Self-Organizing Feature Map). Давайте познакомимся со структурой поближе.

Карты Кохонена имеют набор входных элементов, количество которых совпадает с размерностью подаваемых на вход векторов, и набор выходных элементов, каждый из которых соответствует одному кластеру (группе). Если мы анализируем спортсменов по 4 признакам - скорость бега, рост, вес, выносливость, то, соответственно, мы должны иметь 4 входа, по одному для каждого признака. В этом случае в качестве входного вектора выступает один из спортсменов, а его координатами являются значения его признаков. Не знаю, удачную ли я выбрал аналогию, но надеюсь, что на таких примерах суть работы станет понятнее.

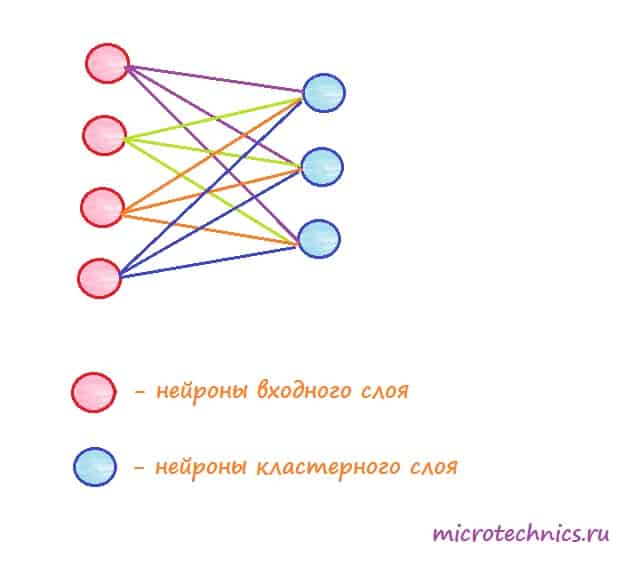
Обычно стараются задавать количество выходных элементов меньше, чем количество входных, в таком случае сеть позволяет позволяет получить упрощенную характеристику объектов для дальнейшей работы с ними.

Также необходимо остановиться на структуре связей между элементами сети. Тут все просто - каждый входной элемент соединяется с каждым выходным, и все связи, также как и для других типов нейронных сетей, имеют определенный вес, который корректируется в процессе обучения.

Но прежде, чем переходить к обсуждению тонкостей обучения, давайте разберемся, как вообще сеть должна работать.

Итак, при подаче какого-либо вектора на вход сеть должна определить, к какому из кластеров этот вектор ближе всего. В качестве критерия близости может быть выбран критерий минимальности квадрата евклидова расстояния. Рассмотрим входной вектор как точку в n-мерном пространстве (n - количество координат вектора, это число равно числу входных нейронов, как мы обсуждали ранее). Тогда нам нужно вычислить расстояние между этой точкой и центрами разных кластеров и определить, расстояние до какого из кластеров окажется минимальным. Тогда этот кластер (и соответствующий ему выходной нейрон) объявляется победителем.

А какая же точка является центром кластера и какие у нее координаты в этом пространстве? Тут все очень изящно 👍 Координатами центра кластера являются величины весов всех связей, которые приходят к данному выходному нейрону от входных элементов. Поскольку каждый выходной нейрон (кластер) соединен с каждым входным нейроном, то мы получаем n связей, то есть n координат для точки, соответствующей центру кластера. Формула для вычисления квадрата евклидова расстояния выглядит следующим образом:

Здесь d_ - квадрат расстояния между точкой P и кластером K . Координаты точки P - , x_. x_> , а координаты центра кластера K - , x_. x_> .

Таким образом, подав вектор на вход сети, мы получим один кластер-победитель, соответственно, этот вектор будет принадлежать именно к этому кластеру (группе). Именно так карты Кохонена и решают задачу классификации.

Обучение нейронной сети Кохонена.

Давайте теперь перейдем к процессу обучения, ведь прежде чем сеть начнет правильно группировать элементы в кластеры, необходимо ее обучить должны образом. Суть обучения состоит в следующем. На вход подается вектор из обучающей выборки. Для этого вектора определяется кластер-победитель, и для этого кластера производят коррекцию весовых коэффициентов таким образом, чтобы он оказался еще ближе ко входному вектору. Чаще всего также корректируют веса нескольких соседей кластера-победителя.

В отличие от обучения с учителем, рассмотренного ранее, суть обучения состоит не в том, чтобы сравнивать вывод сети с идеальным выводом, а в подстройке весов всех связей для максимального совпадения со входными данными.

Для корректировки весов используется следующая формула:

В этой формуле w_(t+1) - вес на шаге t+1 , а w_(t) - вес на шаге t (то есть на предыдущем). \eta - норма обучения, а x_i - координата входного вектора. Обратите внимание, что норма обучения также зависит от номера шага и меняется в процессе обучения. Кроме того, меняется и радиус, определяющий, какое количество элементов сети будут подвергнуты корректировке весов. Давайте разберем подробнее, что определяет этот радиус.

Выходные (кластерные) элементы сети Кохонена обычно представляют расположенными тем или иным образом в двумерном пространстве. Разместим, к примеру, выходные элементы в виде квадратной сетки и зададим начальный радиус обучения равным 2. Подаем на вход сети вектор и элементом-победителем оказывается нейрон, обозначенный на схеме красным цветом. По алгоритму обучения мы должны обновить значения весов для этого нейрона, а также для тех, которые попадают в круг заданного радиуса (в данном случае 2) - эти элементы выделены зеленым:

Ближе к концу процесса обучения радиус уменьшается. Пусть он стал равным единице, тогда обновляться будут веса следующих элементов:

Итак, разобрав все составляющие процесса обучения, давайте напишем конкретный алгоритм для этого процесса:

берем учебный вектор и вычисляем квадрат евклидова расстояния от него до каждого из кластерных элементов сети
находим минимальное из полученных значений и определяем элемент-победитель
для нейрона-победителя, а также для тех нейронов, которые попали в заданный радиус, выполняем корректировку весов связей
обновляем значения нормы обучения и радиуса
продолжаем обучение, если не выполнено условие остановки обучения
остановка обучения происходит в том случае, если величины изменения весов становятся очень малы

И на этом моменте предлагаю сегодня остановиться, поскольку статья получилась довольно объемной, обязательно продолжим в следующей статье.

По способам настройки входных весов сумматоров и по решаемым задачам различают много разновидностей сетей Кохонена. [1] Наиболее известные из них:

Сети векторного квантования сигналов [1] , тесно связанные с простейшим базовым алгоритмом кластеризации (метод динамических ядер или K-средних, то есть K-means)
Самоорганизующиеся карты Кохонена (Self-Organising Maps, SOM) [1]
Сети векторного квантования, обучаемые с учителем (Learning Vector Quantization) [1]

Содержание

Слой Кохонена

Базовая версия

Слой Кохонена состоит из некоторого количества параллельно действующих линейных элементов. Все они имеют одинаковое число входов и получают на свои входы один и тот же вектор входных сигналов . На выходе го линейного элемента получаем сигнал

где — весовой коэффициент го входа го нейрона, — пороговой коэффициент.

Геометрическая интерпретация

Разбиение плоскости на многоугольники Вороного-Дирихле для случайно выбранных точек (каждая точка указана в своём многоугольнике).

Последнее слагаемое одинаково для всех нейронов, поэтому для нахождения ближайшей точки оно не нужно. Задача сводится к поиску номера наибольшего из значений линейных функций:

Таким образом, координаты точки совпадают с весами линейного нейрона слоя Кохонена (при этом значение порогового коэффициента ).

Если заданы точки , то -мерное пространство разбивается на соответствующие многогранники Вороного-Дирихле : многогранник состоит из точек, которые ближе к , чем к другим (). [1]

Сети векторного квантования

Задача векторного квантования с кодовыми векторами для заданной совокупности входных векторов ставится как задача минимизации искажения при кодировании, то есть при замещении каждого вектора из соответствующим кодовым вектором. В базовом варианте сетей Кохонена используется метод наименьших квадратов и искажение вычисляется по формуле

где состоит из тех точек , которые ближе к , чем к другим (). Другими словами, состоит из тех точек , которые кодируются кодовым вектором .

Если совокупность задана и хранится в памяти, то стандартным выбором в обучении соответствующей сети Кохонена является метод K-средних. Это метод расщепления:

при данном выборе кодовых векторов (они же весовые векторы сети) минимизацией находим множества — они состоит из тех точек , которые ближе к , чем к другим ;
при данном разбиении на множества минимизацией находим оптимальные позиции кодовых векторов — для оценки по методу наименьших квадратов это просто средние арифметические:

где — число элементов в .

Далее итерируем. Этот метод расщепления сходится за конечное число шагов и даёт локальный минимум искажения.

где — шаг обучения. Остальные кодовые векторы на этом шаге не изменяются.

Для обеспечения стабильности используется онлайн метод с затухающей скоростью обучения: если — количество шагов обучения, то полагают . Функцию выбирают таким образом, чтобы монотонно при и чтобы ряд расходился, например, .

Векторное квантование является намного более общей операцией, чем кластеризация, поскольку кластеры должны быть разделены между собой, тогда как совокупности для разных кодовых векторов не обязательно представляют собой раздельные кластеры. С другой стороны, при наличии разделяющихся кластеров векторное квантование может находить их и по-разному кодировать.

Самоорганизующиеся карты Кохонена

Идея и алгоритм обучения

где — шаг обучения. Соседи кодового вектора — победителя (по априорно заданной таблице близости) сдвигаются в ту же сторону, что и этот вектор, пропорционально мере близости.

Чаще всего, таблица кодовых векторов представляется в виде фрагмента квадратной решётки на плоскости, а мера близости определяется, исходя из евклидового расстояния на плоскости.

Самоорганизующиеся карты и главные многообразия

Самоорганизующиеся карты могут рассматриваться как аппроксимации главных многообразий и популярны в этом качестве [1] .

Упругие карты

Визуализация набора данных по экспрессии генов в раке молочной железы с использованием упругих карт (b) и метода главных компонент (c). Классы точек показаны с использованием размера (ER - статуc эстроген-рецептора), формы (GROUP - риск развития метастаз) и цвета (TYPE - молекулярный тип опухоли). На панели (a) показана конфигурация узлов двумерной упругой карты в проекции на первые три главные компоненты. Сравнивая (b) и (c), можно заметить, что базальный тип опухоли как кластер лучше отделен на нелинейной проекции (b).

Пусть задана совокупность входных векторов . Так же, как и сети векторного квантования и самоорганизующиеся карты, упругая карта представлена как совокупность кодовых векторов (узлов) в пространстве сигналов. Множество данных разделено на классы , состоящие из тех точек , которые ближе к , чем к другим (). Искажение кодирования

может трактоваться как суммарная энергия пружин единичной жёсткости, связывающих векторы данных с соответствующими кодовыми векторами.

энергия растяжения энергия изгиба

где — соответствующие модули упругости.

Задача построения упругой карты состоит в минимизации функционала

Если разбиение совокупности входных векторов на классы фиксировано, то минимизация — линейная задача с разреженной симметричной матрицей коэффициентов. Поэтому, как и для сетей векторного квантования, применяется метод расщепления: фиксируем — ищем — для данных ищем — для данных ищем — … Алгоритм сходится к (локальному) минимуму .

Метод упругих карт позволяет решать все задачи, которые решают самоорганизующиеся карты Кохонена, однако обладает большей регулярностью и предсказуемостью. При увеличении модуля изгиба упругие карты приближаются к линейным главным компонентам. При уменьшении обоих модулей упругости они превращаются в Кохоненовские сети векторного квантования. В настоящее время упругие карты интенсивно используются для анализа многомерных данных в биоинформатике. [1] Соответствующее программное обеспечение опубликовано и свободно доступно на сайте Института Кюри (Париж). [1] [1]

На рисунке представлены результаты визуализации данных по раку молочной железы. Эти данные содержат 286 примеров с указанием уровня экспрессии 17816 генов [1] . Они доступны онлайн как ставший классическим тестовый пример для визуализации и картографии данных [1] .

Сети векторного квантования, обучаемые с учителем

Решается задача классификации. Число классов может быть любым. Изложим алгоритм для двух классов, и . Исходно для обучения системы поступают данные, класс которых известен. Задача: найти для класса некоторое количество кодовых векторов , а для класса некоторое (возможно другое) количество кодовых векторов таким образом, чтобы итоговая сеть Кохонена с кодовыми векторами , (объединяем оба семейства) осуществляла классификацию по следующему решающему правилу:

С каждым кодовым вектором объединённого семейства связан многогранник Вороного-Дирихле. Обозначим эти многогранники , соответственно. Класс в пространстве сигналов, согласно решающему правилу, соответствует объединению , а класс соответствует объединению . Геометрия таких объединений многогранников может быть весьма сложной (см. Рис с примером возможного разбиения на классы).

Это — простейшая (базовая) версия метода [1] . Существует множество других модификаций.

Учебное програмное обеспечение

Ссылки

Сети векторного квантования сигналов [1] , тесно связанные с простейшим базовым алгоритмом кластеризации (метод динамических ядер или K-средних, то есть K-means)
Самоорганизующиеся карты Кохонена (Self-Organising Maps, SOM) [1]
Сети векторного квантования, обучаемые с учителем (Learning Vector Quantization) [1]