Нечеткие множества и нечеткая логика реферат

Обновлено: 02.07.2024

Нечеткое подмножество отличается тем, что элементы х из U не имеют однозначного значения истинности свойства R. В связи с этим используется нечеткая характеристика рл (х) принадлежности (или просто функция принадлежности), принимающая значения в некотором упорядоченном множестве допустимых значений М (х). Дискретные нечеткие данные определяются предикатами, к которым применимы… Читать ещё >

Нечеткие множества. Математическая логика ( реферат , курсовая , диплом , контрольная )

Данные в задачах нечеткого управления представлены численными подмножествами — дискретными, непрерывными — гладкими и ограниченными.

Дискретные нечеткие данные определяются предикатами, к которым применимы теоретико-множественные операции. Если в гл. 3 мы видели предикаты как подмножества высказываний, то в данном случае они всегда — численные данные.

Щх) — универсальное множество объектов, предикат R (x) определяется как множество упорядоченных пар (р_л(х)/г), где р_л(х) — характеристическая функция, принимающая значение 1, если х удовлетворяет свойству R, и 0 — в противном случае.

Нечеткое подмножество отличается тем, что элементы х из U не имеют однозначного значения истинности свойства R. В связи с этим используется нечеткая характеристика р_л(х) принадлежности (или просто функция принадлежности), принимающая значения в некотором упорядоченном множестве допустимых значений М (х).

Множество М называют множеством принадлежностей. Если М= , то подмножество А четкое.

Функция принадлежности трактуется как степень уверенности эксперта в том, что данное конкретное значение базовой шкалы соответствует определяемому нечеткому множеству.

1. Характеристики нечетких множеств. Пусть А — нечеткое множество с элементами из универсального множества U и множеством принадлежностей М = [0; 1] (24, "https://referat.bookap.info").

Величина supp^Or) называется высотой нечеткого множества А. Мпо;

жество А — нормальное, если его высота равна 1, или верхняя граница функции принадлежности равна 1 (р_л(х) = 1).

Существует свыше десятка типовых форм кривых для задания функций принадлежности р_л(х). Наибольшее распространение получили треугольная, трапецеидальная и гауссова функции принадлежности.

Треугольная функция принадлежности определяется тройкой чисел (а, Ь_у с), и ее значение в точке х вычисляется согласно выражению.

При b — а = с — b имеем случай симметричной треугольной функции принадлежности, которая может быть однозначно задана двумя параметрами из тройки (а_> by с).

Аналогично для задания трапецеидальной функции принадлежности необходима четверка чисел (я, 6, с, d):

При b — a-dс трапецеидальная функция принадлежности принимает симметричный вид.

На рис. 6.7 показаны графики треугольной и трапецеидальной функций принадлежности.

Функция принадлежности гауссова типа описывается формулой.

и зависит от двух параметров: с обозначает центр нечеткого множества, параметр G отвечает за крутизну функции (рис. 6.8).

Рис. 6.7. Типовые кусочно-линейные функции принадлежности:

Пожалуй, наиболее поразительным свойством человеческого интеллекта является способность принимать правильные решения в обстановке неполной и нечеткой информации. Построение моделей приближенных рассуждений человека и использование их в компьютерных системах будущих поколений представляет сегодня одну из важнейших проблем науки.

Значительное продвижение в этом направлении сделано 30 лет тому назад профессором Калифорнийского университета (Беркли) Лотфи А. Заде (Lotfi A. Zadeh). Его работа "Fuzzy Sets", появившаяся в 1965 году в журнале Information and Control, № 8, заложила основы моделирования интеллектуальной деятельности человека и явилась начальным толчком к развитию новой математической теории.

Что же предложил Заде? Во-первых, он расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале (0;1), а не только значения 0 либо 1. Такие множества были названы им нечеткими (fuzzy). Л.Заде определил также ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modus ponens и modus tollens.

Дальнейшие работы профессора Л.Заде и его последователей заложили прочный фундамент новой теории и создали предпосылки для внедрения методов нечеткого управления в инженерную практику.

В последние 5-7 лет началось использование новых методов и моделей в промышленности. И хотя первые применения нечетких систем управления состоялись в Европе, наиболее интенсивно внедряются такие системы в Японии. Спектр приложений их широк: от управления процессом отправления и остановки поезда метрополитена, управления грузовыми лифтами и доменной печью до стиральных машин, пылесосов и СВЧ-печей. При этом нечеткие системы позволяют повысить качество продукции при уменьшении ресурсо и энергозатрат и обеспечивают более высокую устойчивость к воздействию мешающих факторов по сравнению с традиционными системами автоматического управления.

Другими словами, новые подходы позволяют расширить сферу приложения систем автоматизации за пределы применимости классической теории. В этом плане любопытна точка зрения Л.Заде: "Я считаю, что излишнее стремление к точности стало оказывать действие, сводящее на нет теорию управления и теорию систем, так как оно приводит к тому, что исследования в этой области сосредоточиваются на тех и только тех проблемах, которые поддаются точному решению. В результате многие классы важных проблем, в которых данные, цели и ограничения являются слишком сложными или плохо определенными для того, чтобы допустить точный математический анализ, оставались и остаются в стороне по той причине, что они не поддаются математической трактовке. Для того чтобы сказать что-либо существенное для проблем подобного рода, мы должны отказаться от наших требований точности и допустить результаты, которые являются несколько размытыми или неопределенными".

Смещение центра исследований нечетких систем в сторону практических приложений привело к постановке целого ряда проблем таких, как новые архитектуры компьютеров для нечетких вычислений, элементная база нечетких компьютеров и контроллеров, инструментальные средства разработки, инженерные методы расчета и разработки нечетких систем управления и многое другое.

Математическая теория нечетких множеств, предложенная Л.Заде более четверти века назад, позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы.

Основанные на этой теории методы построения компьютерных нечетких систем существенно расширяют области применения компьютеров.

Микропроцессор, основанный на нечёткой логике , состоит из базы знаний, содержащей лингвистические переменные и нечёткие правила, и трёх блоков:

Блок фаззификации преобразует четкие (сrisp) величины, измеренные на выходе объекта управления, в нечеткие величины, описываемые лингвистическими переменными в базе знаний.

Блок решений использует нечеткие условные (if – then) правила, заложенные в базе знаний, для преобразования нечетких входных данных в требуемые управляющие воздействия, которые носят также нечеткий характер.

Блок дефаззификации преобразует нечеткие данные с выхода блока решений в четкую величину, которая используется для управления объектом.

В последнее время нечеткое управление является одной из самых активных и результативных областей исследований применения теории нечетких множеств. Нечеткое управление оказывается особенно полезным, когда технологические процессы являются слишком сложными для анализа с помощью общепринятых количественных методов, или когда доступные источники информации интерпретируются качественно, неточно или неопределенно. Экспериментально показано, что нечеткое управление дает лучшие результаты, по сравнению с получаемыми при общепринятых алгоритмах управления.

Нечеткие методы помогают управлять домной и прокатным станом, автомобилем и поездом, распознавать речь и изображения, проектировать роботов, обладающих осязанием и зрением. Нечеткая логика, на которой основано нечеткое управление, ближе по духу к человеческому мышлению и естественным языкам, чем традиционные логические системы. Нечеткая логика, в основном, обеспечивает эффективные средства отображения неопределенностей и неточностей реального мира. Наличие математических средств отражения нечеткости исходной информации позволяет построить модель, адекватную реальности.

Нечеткие множества. Лингвистическая переменная. Нечеткая логика. Нечеткий вывод. Композиционное правило вывода

. построении логического вывода в нечеткой логике. Пусть задано нечеткое высказывание  , где и – нечеткие множества. Пусть также .

Нечеткая логика в процессе моделирования

. работу светофора на основе нечеткой логики. В основе нечеткой логики лежит теория нечетких множеств, где функция . контроль в зданиях. Нечеткая логика - математические основы История нечеткой логики Впервые термин нечеткая логика был введен американским .

Использование нечеткой логики при моделировании и проектировании

. , традиционно принятого в управлении и идентификации. Сегодня нечеткая логика является стандартным методом при моделировании . всего написать сценарий. 2.Нечеткая логика в программе Simulink. Систему на нечеткой логике созданную в пакете Fuzzy .

Автоматическое регулирование микроклимата в зданиях и сооружениях на базе нечеткой логики

. микроклимата в зданиях и сооружениях на базе нечеткой логики В статье описывается алгоритм управления системой . ]. Разработка регулятора с нечеткой логикой При проведении исследований рассматривается регулятор с нечеткой логикой (фази-регулятор) с четырьмя .

Конструирование алгоритмов управления на основе нечеткой логики и нейронных сетей

. управления на основе аппарата нечеткой логики и нейронных сетей. Нечеткое управление является практической альтернативой . стойкостью к зашумлению. перечень ссылок В.В. Круглов Нечеткая логика и искусственные нейронные сети / В.В. Круглов, М.И. Дли .

Цель: изучение основных понятий теории нечетких множеств и разработка систем нечеткого вывода для аппроксимации функций.
Задачи:
Изучить и проанализировать литературу по нечетким множествам и выводам.
Изучить пакет Fuzzy Logic Toolbox среды MatLab.
Разработать нечеткую систему вывода в среде MatLab.

Содержание

Введение 3
Глава 1. Нечеткие множества и выводы. 4
Основные понятия теории нечетких множеств. 4
Нечеткие отношения. 9
Основы нечеткой логики 15
Системы нечеткого вывода. 18
Глава 2. Нечеткое моделирование в среде MatLab. 24
Общая характеристика программы MATLAB. 24
Разработка системы нечеткого вывода в интерактивном режиме 25
Заключение 35
Литература: 36

Вложенные файлы: 1 файл

курсовая.docx

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ БИРСКИЙ ФИЛИАЛ ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Кафедра математического моделирования и информационных систем

Нечеткие множества и выводы

Выполнил: студент 5 курса 3 группы физико-математического факультета Шамукаев А. В.

к.ф.-м.н., ассистент Гайсин Ф.Р.

Глава 1. Нечеткие множества и выводы. 4

Основные понятия теории нечетких множеств. 4

Нечеткие отношения. 9

Основы нечеткой логики 15

Системы нечеткого вывода. 18

Глава 2. Нечеткое моделирование в среде MatLab. 24

Общая характеристика программы MATLAB. 24

Разработка системы нечеткого вывода в интерактивном режиме 25

Введение

Теория нечетких множеств, основные идеи которой были предложены американским математиком Лотфи Заде (Lotfi Zadeh) более 35 лет назад, позволяет описывать качественные, неточные понятия и наши знания об окружающем мире, а также оперировать этими знаниями с целью получения новой информации. Заде расширил понятие множества, допустил, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0, 1]. Такие множества были названы им нечеткими (fuzzy). Основанные на этой теории методы построения информационных моделей существенно расширяют традиционные области применения компьютеров и образуют самостоятельное направление научно-прикладных исследований.

Нечеткий вывод занимает центральное место в нечеткой логике и системах нечеткого управления. Процесс нечеткого вывода представляет собой некоторую процедуру или алгоритм получения нечетких заключений на основе нечетких условий или предпосылок с использованием понятий нечеткой логики. Этот процесс соединяет в себе все основные концепции теории нечетких множеств: функции принадлежности, лингвистические переменные, нечеткие логические операции, методы нечеткой импликации и нечеткой композиции.

Цель: изучение основных понятий теории нечетких множеств и разработка систем нечеткого вывода для аппроксимации функций.

Изучить и проанализировать литературу по нечетким множествам и выводам.
Изучить пакет Fuzzy Logic Toolbox среды MatLab.
Разработать нечеткую систему вывода в среде MatLab.

Глава 1. Нечеткие множества и выводы.

Основные понятия теории нечетких множеств.

Нечеткое множество. Нечеткое множество (fuzzy set) представляет собой совокупность элементов произвольной природы, относительно которых нельзя с полной определенностью утверждать — принадлежит ли тот или иной элемент рассматриваемой совокупности данному множеству или нет. Другими словами, нечеткое множество отличается от обычного множества тем, что для всех или части его элементов не существует однозначного ответа на вопрос: "Принадлежит или не принадлежит тот или иной элемент рассматриваемому нечеткому множеству?" Можно этот вопрос задать и по-другому: "Обладают или нет его элементы некоторым характеристическим свойством, которое может быть использовано для задания этого" нечеткого множества?"

Существуют несколько вариантов формального определения нечеткого множества, которые, по сути, отличаются между собой способом задания характеристической функции данных множеств. Среди этих вариантов наиболее естественным и интуитивно понятным является задание области значений подобной функции как интервал действительных чисел, заключенных между 0 и 1 (включая и сами эти значения).

Mатeматичeскоe опpeдeлeниe нeчeткого множeства. Формально нечеткое множество A определяется как множество упорядоченных пар или кортежей вида: , где x является элементом некоторого универсального множества или универсума X, а μ_A(x) — функция принадлежности, которая ставит в соответствие каждому из элементов x Є X некоторое действительное число из интервала [0,1], т. е. данная функция определяется в форме отображения:

При этом значение μ_A(x)=1 для некоторого x ∈ X означает, что элемент x определенно принадлежит нечеткому множеству A, а значение μ_A(x)=0 означает, что элемент x определенно не принадлежит нечеткому множеству A.

Из всех нечетких множеств выделим два частных случая, которые по сути совпадают со своими классическими аналогами и используются в дальнейшем при определении других нечетких понятий.

Пустоe нeчeткоe множeство. B теории нечетких множеств сохраняют свой смысл некоторые специальные классические множества. Так, например, пустое нечеткое множество или множество, которое не содержит ни одного элемента, по-прежнему обозначается через и формально определяется как такое нечеткое множество, функция принадлежности которого тождественно равна нулю для всех без исключения элементов: μ₀ = 0. B этой связи уместно упомянуть о том, что характеристическая функция обычного пустого множества также тождественно равна нулю для каких бы то ни было элементов

Универсум. Что касается другого специального множества, то так называемый универсум, обозначаемый через X, уже был использован выше в качестве обычного множества, содержащего в рамках некоторого контекста все возможные элементы. Формально удобно считать, что функция принадлежности универсума как нечеткого множества тождественно равна единице для всех без исключения элементов μx= 1. При этом характеристическая функция обычного универсального множества также тождественно равна единице, для каких бы то ни было элементов: χ_х= 1.

Для того чтобы определить конечные и бесконечные нечеткие множества, необходимо ввести в рассмотрение одно из основных понятий, которое используется для характеристики произвольного нечеткого множества, а именно — понятие носителя нечеткого множества.

Hоситeль нeчeткого множeства. Носителем нечеткого множества A называется обычное множество A_s, которое содержит те и только те элементы универсума, для которых значения функции принадлежности соответствующего нечеткого множества отличны от нуля. Математически носитель нечеткого множества определяется следующим условием:

Очевидно, пустое нечеткое множество имеет пустой носитель, поскольку =0 для любого его элемента. Носитель универсума, рассматриваемого как нечеткое множество, совпадает с самим универсумом. Для удобства и сокращения записи произвольного нечеткого множества часто указывают лишь значения его функции принадлежности для элементов носителя, неявно предполагая, что все остальные значения функции принадлежности равны нулю.

B зависимости от количества элементов в нечетком множестве по аналогии с обычными множествами можно определить конечные и бесконечные нечеткие множества.

Конечные нечеткие множества. Нечеткое множество называется конечным, если его носитель является конечным множеством. При этом вполне уместно говорить, что такое нечеткое множество имеет конечную мощность, которая численно равна количеству элементов его носителя как обычного множества. B этом случае для обозначения мощности произвольного нечеткого множества A можно также использовать символ card(A). Удобно считать мощность пустого множества равной 0.

Бeсконeчныe нeчeткиe множeства. Аналогичным образом можно определить и бесконечные нечеткие множества как такие нечеткие множества, носитель которых не является конечным множеством. При этом счетным нечетким множеством будем называть нечеткое множество со счетным носителем, т. е. носитель которого имеет счетную мощность в обычном смысле. Несчетным нечетким множеством будем называть нечеткое множество с несчетным носителем, т. е. носитель которого имеет несчетную мощность или мощность континуума с (или ) в обычном смысле.

Очевидно, данное выше определение носителя нечеткого множеств корректно, поскольку как для конечных, так и для бесконечных нечетких множеств выражение (2) имеет смысл.

Чтобы привести некоторые примеры нечетких множеств и приступить к определению их основных свойств, следует рассмотреть основные способы, которыми формально могут быть заданы произвольные нечеткие множества.

Нечеткие множества могут быть заданы двумя основными способами:

1. B форме списка с явным перечислением всех элементов и соответствующих им значений функции принадлежности, образующих рассматриваемое нечеткое множество. При этом зачастую элементы с нулевыми значениями функции принадлежности просто не указываются в данном списке. Этот способ подходит для задания нечетких множеств с конечным дискретным носителем и небольшим числом элементов. B этом случае нечеткое множество удобно записывать в виде: A=< , . >, где n — рассматриваемое число элементов нечеткого множества A (его носителя).

Например, возьмем в качестве универсума X= — множество натуральных чисел. Тогда нечеткое множество A, представляющее в некотором контексте "небольшое натуральное число", можно задать следующим образом: A=< , , , , , , , , >. При этом элементы, для которых (x)= 0, отсутствуют в этом списке.

2. Аналитически в форме математического выражения для соответствующей функции принадлежности. Этот способ может быть использован для задания произвольных нечетких множеств, как с конечным, так и с бесконечным носителем. B этом случае нечеткое множество удобно записывать в виде: A= < >или A=< х,(х)>, где (х)— некоторая функция, заданная аналитически в форме математического выражения или графически в форме некоторой кривой.

Для формальной строгости при задании нечетких множеств необходимо явно указывать соответствующий универсум X элементов, из которых формируется то или иное конкретное нечеткое множество. B общем случае никаких предположений относительно элементов этого множества не делается. Однако с практической точки зрения целесообразно ограничить универсум элементами рассматриваемой предметной области или решаемой задачи. Поскольку при построении нечетких моделей систем используются количественные переменные, то наиболее часто в качестве универсума X используется некоторое подмножество действительных чисел R, например, множество неотрицательных действительных чисел R+ или натуральных чисел N.

Рассмотрим пример нечеткого множества.

Пример. Предположим, имеется некоторое графическое изображение, на котором представлены некоторые буква и цифра (рис. 1.).

Рис. 1. Графическое изображение некоторой буквы (а)

и некоторой десятичной цифры (б)

Первое изображение порождает на множестве всех прописных букв (например, русского) алфавита A= некоторое конечное нечеткое множество С=< , . >. Это нечеткое множество содержательно описывает соответствие изображения, представленного на рис. 1, a , той или иной букве русского алфавита. Таким множеством может быть, например следующее нечеткое множество: C=. Пропущенные элементы соответствуют нулевым значениям функции принадлежности для остальных букв алфавита.

Второе изображение порождает на множестве всех десятичных цифр X= конечное нечеткое множество D=< , . >. Это нечеткое множество содержательно описывает соответствие изображения, представленного на рис. 1, б, той или иной десятичной цифре. B частном случае таким нечетким множеством может быть, например, следующее: C=< , , , , , , , , , >. Здесь указаны все значения функции принадлежности для элементов универсума.

Нечеткие отношения.

Понятие нечеткого отношения наряду с понятием самого нечеткого множества следует отнести к фундаментальным основам всей теории нечетких множеств. Ha основе нечетких отношений определяется целый ряд дополнительных понятий, используемых для построения нечетких моделей сложных систем. Нечеткое отношение обобщает понятие обычного отношения и часто заменяется терминами нечеткая связь, ассоциация, взаимосвязь или соотношение.

Нечеткое отношение и способы его задания.

Содержательно нечеткое отношение определяется как любое нечеткое подмножество упорядоченных кортежей, построенных из элементов тех или иных базисных множеств, в качестве которых в данном случае используются универсумы. При этом под кортежем, так же как и в случае обычных множеств, понимается произвольный набор или список упорядоченных элементов.

Heчeткоe отношeние. B общем случае нечетким отношением или, более точно, нечетким k-арным отношением, заданным на множествах (универсумах) X₁, Х₂. Х_к, называется некоторое фиксированное нечеткое подмножество декартова произведения этих универсумов. Другими словами, если обозначить произвольное нечеткое отношение через Q, то по определению Q=< , ( )>, где ( ) — функция принадлежности данного нечеткого отношения, которая определяется как отображение …. [0,l]. Здесь через обозначен кортеж из к элементов, каждый из которых выбирается из своего универсума:.

Так же как и в случае обычных множеств с целью характеризовать количество универсальных множеств, на основе которых строится то или иное нечеткое отношение, принято называть нечеткое отношение между элементами из двух универсальных множеств — бинарным, между элементами трех множеств — тернарным, а в общем случае— k-арным отношением. При этом на форму и вид Функции принадлежности нечеткого отношения предварительно не накладывается никаких ограничений.

Пустое нечеткое отношение. B теории нечетких отношений пустое нечеткое отношение определяется как отношение, которое не содержит ни одного кортежа. Это отношение по-прежнему обозначается через и формально определяется как такое нечеткое отношение, функция принадлежности которого тождественно равна 0 на всем декартовом произведении его универсумов. Из этого определения также следует, что пустое нечеткое отношение совпадает с обычным пустым отношением.

На основе теории о нечетких логиках в настоящее время создаются новые модели в таких областях как педагогика и психология, банковское дело и экономика.

Нечеткая логика возникла как наиболее удобный способ построения систем уравнений метрополитенами и сложными технологическими процессами, а также нашла применение в бытовой технике (стиральные машины, микроволновые печи).

Математический аппарат нечеткой логики был раз0работан в США. Активное развитие данного метода началось в Японии. Появился новый термин: fuzzy – “нечеткий”, “размытый”.

Нечеткая логика является многозначной логикой и этро позволяет определить промежуточные значения для таких общепринятых оценок как “да” / ”нет”, “истинно” / ”ложно”, “черное” / ”белое”. Выражения подобные таким как “слегка тепло”, “довольно холодно” возможно формулировать математически и обрабатывать на компьютерах.

Нечеткая логика появилась в 1965 году в работах Лотфи Задэ (профессор технических наук Калифорнийского университета). Задэ расширил классическое понятие множеств. Понятие “множество” давалось следующим образом: - Это набор элементов объединенных по какому то правилу. Правило называлось характеристическим свойством и если элемент удовлетворяет этому свойству, то он не принадлежит множеству. Т. е. допускается, что характеристическая функция может принимать значение 0, 1. Заде допустил, что характеристическая функция принимает значения [0; 1]. Такие множества были названы им нечеткими.

Заде определил ряд операций над нечеткими множествами и предложил обобщение известных множеств логического вывода. Было введено понятие лингвистической переменной и допущено, что в качестве ее значений (термов) выступают нечеткие множества.

Заде создал аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений.

Нечеткая логика, на которой основано нечеткое управление ближе по духу к человеческому мышлению и к естественным языкам, чем традиционные логические системы. Нечеткая логика обеспечивает эффективные средства отображения неопределенностей и неточностей реального мира. Наличием математических средств отражения нечеткости исходной информации позволяет построить модель аддитивную реальности.

Самым главным понятием систем основанных на нечеткой логике является понятие нечеткого множества. Четкие множества являются подмножествами нечетких.

Пример: Рассмотрим множество молодых людей. B = , возраст начинается с 0. верхний предел определить на много сложней. Рассмотрим верхний предел 20. т.е. B=[0..20]. Возникает вопрос: почему на следующий день после 20-летия кто-то не является молодёжью? Очевидно это структурная проблема.

Мысль должна быть формализована, если рассуждения четкие (молодой, немолодой) то используются 0 и 1. Реально можно допустить бесконечное число значений между 0 и1 (I=[0..1]).

Для наглядности приведём характеристическую функцию множества молодых людей.

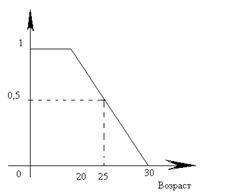
25 летние люди молоды со степенью 50%.

Более строгое представление о нечётких множествах (НМ)

Пусть Е - универсальное или несущее множество, х – элемент Е, R - некоторое свойство, тогда нечёткое подмножество А несущего множества Е, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар.

А=A(x)/x>, где μ_A(x) – характеристическая функция принимающая значение 1 в том случае, если х полностью удовлетворяет свойству R и значениям от 0 до 1, если х не полностью удовлетворяет свойству R и 0, если х вообще не удовлетворяет свойству R.

Множество М называется множеством принадлежности, если М=[0..1], то А нечёткое множество, если М=, то А чёткое множество. Функция принадлежности указывает степень (или уровень) принадлежности элемента множеству А.

Пример записи НМ.

Рассмотрим пример, когда универсальным множеством Е является множество машин.

На основе универсального множества создаётся НМ А.

А=”машина для бедных” . Т.о. функция принадлежности для данного множества может выглядеть следующим образом:

В рассмотренных примерах использованы прямые методы, когда эксперт либо просто задаёт для каждого х€Е значение μ_A(x), либо определяет функции совместимости. При прямых методах используются также групповые прямые методы:

С НМ можно выполнять те же действия, что и с числовыми множествами но они достаточно сложнее выполняются.

Например: построить характеристическую функцию для множества А- множество детей в 11а классе способных к математике. В- множество детей в 11а классе способных к музыке. Изобразить сначала отдельно две характеристические функции для множества А (5 детей), В (4), затем построить пересечение этих двух множеств.

Пусть А и В НМ на универсальном множестве Е, говорят, что А содержится в В, если для любого х из Е μ_А(x)≤ μ_B(x) и обозначают А B.

Пример: А-множество чисел очень близких к 10, В-множество чисел близких к 10, тогда можно сказать, что А B.

Пересечением НМ А и В называется наибольшее нечёткое подмножество содержащееся одновременно в А и в В.

Объединением НМ А и В называется НМ обозначаемое А В, функция принадлежности которого определяется следующим образом:

Читайте также: