Методы расчета нелинейных цепей переменного тока реферат

Обновлено: 02.07.2024

Нелинейные электрические цепи

В электрические цепи могут входить пассивные элементы , электрическое сопротивление которых существенно зависит от тока и ли напряжения, в результате чего ток не находится в прямо пропорциональной зависимости по отношению к напряжению. Такие элементы и электрические цепи, в которые они входят, называют нелинейными элементами .

Нелинейные элементы придают электрическим цепям свойства, недостижимые в линейных цепях (стабилизация напряжения или тока, усиление постоянного тока и др.). Они бывают неуправляемые и управляемые . Первые - двухполюсники - предназначены для работы без воздействия на них управляющего фактора (полупроводниковые терморезисторы и диоды), а вторые - многополюсники - используются при воздействии на них управляющего фактора (транзисторы и тиристоры).

Вольт-амперные характеристики нелинейных элементов

Электрические свойства нелинейных элементов представляют вольт-амперными характеристиками I(U) экспериментально полученными графиками, отображающими зависимость тока от напряжения, для которых иногда составляют приближенную, удобную для расчетов эмпирическую формулу.

Неуправляемые нелинейные элементы имеют одну вольт-амперную характеристику, а управляемые - семейство таких характеристик, параметром которого является управляющий фактор.

У линейных элементов электрическое сопротивление постоянно, поэтому вольт-амперная характеристика их является прямой линией, проходящей через начало координат (рис. 1, а).

Вольт-амперные характеристики нелинейных имеют различную форму и разделяются на симметричные и несимметричные относительно осей координат (рис. 1, б, в).

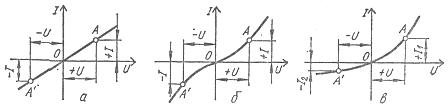
Рис. 1. Вольт-амперные характеристики пассивных элементов: а - линейных, б - нелинейных симметричных, в - нелинейных несимметричных

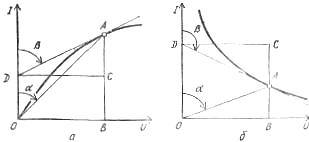
Рис. 2. Графики для определения статического к дифференциального сопротивлений нелинейных элементов на участках вольт-амперных характеристик: а - восходящем, б - падающем

У нелинейных элементов с симметричной вольт-амперной характеристикой, или у симметричных, элементов, перемена направления напряжения не вызывает изменения значения тока (рис. 1, б), а у нелинейных элементов с несимметричной вольт-амперной характеристикой, или у несимметричных элементов, при одном и том же абсолютном значении напряжения, направленного в противоположные стороны, токи разные (рис. 1, в). Поэтому нелинейные симметричные элементы применяют в цепях постоянного и переменного тока, а нелинейные несимметричные элементы, как правило, в цепях переменного тока для преобразования переменного тока в ток постоянного направления.

Характеристики нелинейных элементов

Для каждого нелинейного элемента различают статическое сопротивление, соответствующее данной точке вольт-амперной характеристики, например, точке А:

R ст = U/I = muOB / miBA = mr tgα

и дифференциальное сопротивление, которое для. той же точки А определяется по формуле:

R диф = dU/dI = muDC / miCA = mr tgβ ,

где mu, mi, mr - соответственно масштаб напряжений, токов и сопротивлений.

Статическое сопротивление характеризует свойства нелинейного элемента в режиме неизменного тока, а дифференциальное — при малых отклонениях тока от установившегося значения. Оба они изменяются при переходе от одной точки и вольт-амперной характеристики к другой, причем первое всегда положительное, а второе - знакопеременное: на восходящем участке вольт-амперной характеристики оно положительное, а на падающем участке - отрицательное.

Нелинейные элементы характеризуются также обратными величинами: статической проводимостью Gст и дифференциальной проводимостью G диф либо безразмерными параметрами -

Kr = - (R диф/ R ст)

или относительной проводимостью:

Kg = - ( G диф / G ст)

У линейных элементов параметры Kr и Kg равны единице, а у нелинейных элементов отличаются от нее, причем чем больше они отличаются от единицы, тем больше проявляется нелинейность электрической цепи.

Нелинейные электрические цепи рассчитывают графическим и аналитическим методами , в основу которых положены законы Кирхгофа и вольт-амперные характеристики отдельных элементов цепях переменного тока для преобразования переменного тока в ток постоянного направления.

При графическом расчете электрической цепи с двумя последовательно соединенными нелинейными резисторами R1 и R2 с вольт-амперными характеристиками I(U1) и I(U2) строят вольт-амперную характеристику всей цепи I(U) , где U = U1+U2 , абсциссы точек которой находят суммированием абсцисс точек вольт-амперных характеристик нелинейных резисторов с равными ординатами (рис. 3, а, б).

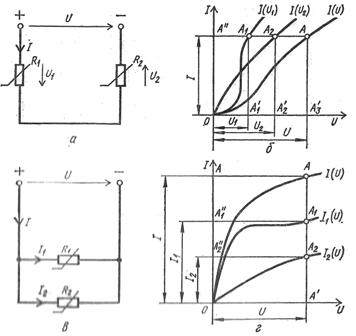
Рис. 3. Схемы и характеристики нелинейных электрических цепей: а - схема последовательного соединения нелинейных резисторов, б - вольт-амперные характеристики отдельных элементов и последовательной цепи, в - схема параллельного соединения нелинейных резисторов, г - вольт-амперные характеристики отдельных элементов и параллельной цепи.

Наличие этой кривой позволяет по напряжению U найти ток I , а также напряжения U1 и U2 на зажимах резисторов.

Аналогично выполняют расчет электрической цепи с двумя параллельно соединенными резисторами R1 и R2 с вольт-амперными характеристиками I1(U) и I 2(U), для чего строят вольт-амперную характеристику всей цепи I ( U ), где I = I1 + I2 , по которой, пользуясь заданным напряжением U , находят токи I , I1 , I2 (рис. 3 , в, г).

Аналитический метод расчета нелинейных электрических цепей основан на представлении вольт-амперных характеристик нелинейных элементов уравнениями соответствующих математических функций, позволяющих составить необходимые уравнения состояния электрических цепей. Поскольку решение таких нелинейных уравнений часто вызывает значительные трудности, аналитический метод расчета нелинейных цепей удобен, когда рабочие участки вольт-амперных характеристик нелинейных элементов могут быть спрямлены. Это позволяет описать электрическое состояние цепи линейными уравнениями, не вызывающими затруднения при их решении.

В теории линейных электрических цепей с постоянными параметрами весь анализ сводится к решению системы линейных дифференциальных или алгебраических уравнений. Математический аппарат для решения подобных уравнений был полностью разработан еще в начале прошлого века. Задача теории в последнее время сводилась к тому, чтобы найти наиболее экономичный и наглядный метод инженерного расчета, анализа или синтеза цепи. При этом для решения всех задач широко применяются принципы наложения и взаимности.

Значительно сложнее обстоит дело с расчетом нелинейных электрических цепей. Сама теория нелинейных дифференциальных уравнений, описывающих процессы в нелинейных электрических цепях, разработана значительно меньше. Для нелинейных уравнений каждого типа существуют свои методы подхода и решения, причем многие нелинейные уравнения не имеют аналитических решений и требуют построения специальных функций. Особенно усложняется расчет нелинейных цепей тем, что в большинстве задач характеристики нелинейного элемента заданы графически и отсутствует достаточно простое математическое описание этих характеристик.

Однако инженерная практика требует получения хотя бы грубо ориентировочных расчетных соотношений, которые дают количественную оценку процессов, происходящих в нелинейных цепях. Именно поэтому в отличие от теории линейных цепей, где может быть получено решение задачи с любой точностью, основой теории нелинейных цепей является получение приближенных решений, дающих в основном качественную оценку процессов.

Развитие теории нелинейных электрических цепей относится в основном к нынешнему веку. В этой области ведущее значение имеют работы русских и советских ученых А. М. Ляпунова, Л. И. Мандельштама, Н. Д. Папалекси, А. А. Андронова, Н. М. Крылова, Н. Н. Боголюбова и многих других. Из зарубежных работ большое значение для развития нелинейной электротехники имели исследования Пуанкаре, Ван-дер-Поля, Рюденберга и др.

Можно назвать следующие методы приближенного расчета нелинейных цепей переменного тока, получившие преимущественное распространение в практике инженерных расчетов.

Разновидностью метода малого параметра является метод гармонического баланса. При расчете цепи этим методом рассматривают амплитуды основных гармонических составляющих токов и напряжений в нелинейной электрической цепи и пренебрегают действием всех высших гармоник. При этом иногда полагают, что амплитуды гармонических составляющих медленно изменяются, но нет необходимости учитывать спектр гармоник, связанных с изменением амплитуды.

Такое упрощение задачи по существу является заменой нелинейной зависимости линейной, справедливой только для определенного значения амплитуд тока или напряжения. Поэтому этот метод иногда называется методом гармонической линеаризации. Он был применен в работах Л. И. Мандельштама и Н. Д. Папалекси, затем в работах Н. М. Крылова и Н. Н. Боголюбова и получил дальнейшее развитие в работах Л. С. Гольдфарба, Е. П. Попова и др. применительно к задачам теории автоматического регулирования.

При расчете переходных процессов метод условной линеаризации основывается на приближенной замене нелинейной функции линейной и применении решений линейного уравнения с последующим уточнением результата введением поправок.

Этот метод дает очень приближенное решение задачи, однако он наиболее прост и поэтому применяется для ориентировочного расчета процессов, анализ которых более точными методами представляет значительные трудности.

2. Метод аналитической аппроксимации нелинейной характеристики. Сущность метода заключается в приближенном выражении нелинейной характеристики некоторой аналитической функцией такого вида, чтобы достаточно просто решалось нелинейное дифференциальное уравнение цепи. Успешное применение метода зависит от того, насколько точно удалось подобрать аналитическое выражение для нелинейной характеристики и насколько просто решается полученное дифференциальное уравнение.

При решении дифференциального уравнения иногда прен гают некоторыми членами ввиду их относительной малости, сматривая их как своего рода малый параметр.

Эгот метод при расчете нелинейных цепей переменного применяется в сочетании с методом гармонической линеариг и дает возможность аналитически найти первую гармонику или напряжения в нелинейной цепи.

3. Метод кусочно-линейной аппроксимации характеристик припасовывания линейных решений. Сущность метода заключается в замене нелинейной характеристики некоторой ломаной и решении задачи методами линейной электротехники. Решить полученные для каждого из участков ломаной, «припасовываю одно к другому соответствующим выбором постоянных интегр вания.

Этот метод получил широкое применение для решения самых различных задач.

4. Итерационный метод. Применяя этот метод, сначала находят приближенное решение, а затем его уточняют путем подстановки решения в исходное уравнение цепи. Итерационные методы применяются в сочетании с методами малого параметра.

5. Графический метод. Сущность метода заключается в сведении дифференциальных уравнений цепи к системе нелинейных уравнений и получении решения графическими построениями.

Этим методом просто и точно рассчитывают переходные процессы в цепях с постоянными э. д с., описываемых дифференци ными уравнениями первого, а в несколько измененном виде — рого порядка. Для установившихся режимов в цепях с переменными э. д. с. этот метод применяется в сочетании с методом малого параметра и условной линеаризации.

Применительно к расчету переходных процессов графические методы качественного анализа процессов получили развитие в работах А. А. Андронова, С. Э. Хайкина и А. А. Витта и известны под названием метода фазового пространства.

6. Метод последовательных интервалов. Сущность метода заключается в замене дифференциального уравнения алгебраическим, содержащим приращения исследуемых величин за соответствующие интервалы времени. Решение задачи получается в результате множества элементарных расчетов, сводимых обычно в таблицу.

При помощи этого метода может быть проведено числеьное решение тех же задач, что и графическим методом. Метод последовательных интервалов менее нагляден, чем графический, и более громоздок, однако он хорошо сочетается с применением цифровых вычислительных машин, применение которых делает этот метод все более и более распространенным.

Из перечисленных методов графический метод наиболее на ден и в то же время дает удовлетворительную точность решения задачи. Однако при помощи графического метода трудно установить общие зависимости. Аналитический метод обычно менее нагляден,

иногда громоздок и менее точен, однако при помощи аналитического расчета удается получить общие расчетные зависимости. Численные итерационные методы и метод последовательных интервалов при малой наглядности и некоторой громоздкости вычислений позволяют получить наиболее точный результат.

В практических задачах обычно применяют то или иное сочетание различных методов расчета. При решении задач надо иметь в виду приближенный характер задания нелинейных зависимостей, которые могут существенно изменяться с течением времени, а особенно при замене деталей устройства. Поэтому простота и наглядность решения часто более желательны, чем точность математического описания нелинейного элемента и полнота исходных уравнений.

В гл. 23—26 рассматриваются различные технические задачи нелинейной электротехники и для расчета применяются перечисленные выше методы.

Все перечисленные методы приобретают особое значение в связи с применением электронных вычислительных машин (ЭВМ) для решения электротехнических задач. Применение ЭВМ для решения конкретных задач при заданных параметрах и характеристиках электрических цепей дает возможность рассчитывать режим в линейных и нелинейных цепях практически любой сложности и с любой требуемой точностью. При этом методы решения линейных и нелинейных задач различаются значительно меньше, чем при аналитических расчетах.

В связи с этим при рассмотрении явлений в нелинейных электрических цепях предпочтение отдается простоте и наглядности метода расчета и возможности суждения о явлении без его точного количественного анализа, который в случае необходимости всегда может быть произведен при помощи ЭВМ.

Особенности нелинейных цепей при переменных токах

Наиболее существенная особенность расчета нелинейных цепей при переменных токах заключается в необходимости учета в общем случае динамических свойств нелинейных элементов, т.е. их анализ следует осуществлять на основе динамических вольт-амперных, вебер-амперных, и кулон-вольтных характеристик.

Если нелинейный элемент является безынерционным, то его характеристики в динамических и статических режимах совпадают, что существенно упрощает расчет. Однако на практике идеально безынерционных элементов не существует. Отнесение нелинейного элемента к классу безынерционных определяется скоростью изменения входных воздействий: если период Т переменного воздействия достаточно мал по сравнению с постоянной времени , характеризующей динамические свойства нелинейного элемента, последний рассматривается как безынерционный; если это не выполняется, то необходимо учитывать инерционные свойства нелинейного элемента.

В качестве примера можно рассмотреть цепь на рис.1 с нелинейным резистором (термистором), имеющим вольт-амперную характеристику (ВАХ), представленную на рис. 2, и характеризующимся постоянной времени нагрева .

Если , то изображающая точка перемещается по прямой 1 и нелинейный резистор характеризуется сопротивлением . При изображающая точка перемещается по кривой 2, и свойства нелинейного резистора определяются сопротивлением . Когда постоянная времени нагрева t НР одного порядка с Т, соотношения между переменными составляюшими напряжения и тока являются более сложными, определяющими сдвиг по фазе между ними.

Другой важной особенностью нелинейных элементов в цепи переменного тока является вызываемое ими появление высших гармоник даже при наличии в цепи только источников синусоидального напряжения и (или) тока. На этом принципе строится, например, ряд умножителей частоты, а также преобразователей формы тока или напряжения.

Основные типы характеристик нелинейных элементов в цепях переменного тока

Использование динамических характеристик нелинейных элементов позволяет осуществлять расчет нелинейных цепей для мгновенных значений переменных, т.е. проводить принципиально ее наиболее точный и полный анализ. Однако в целом ряде случаев такой расчет может оказаться достаточно трудоемким или избыточным по своей глубине. Поэтому в зависимости от цели решаемой задачи, а также от требований к точности получаемых результатов, помимо динамической характеристики, могут использоваться нелинейные характеристики по первым гармоникам и для действующих значений (см. табл. 1).

Таблица 1. Определение основных типов характеристик нелинейных элементов

Тип харапктеристики

Определение

Динамическая характеристика (характеристика для мгновенных значений)

Характеристика, связывающая мгновенные значения основных определяющих величин

Используется при анализе цепи по мгновенным значениям

Характеристика по первым гармоникам

Характеристика, связывающая амплитуды (действующие значения) первых гармоник основных определяющих величин.

Если воздействующая величина содержит постоянную составляющую, то нелинейный элемент характеризуется семейством зависимостей, для которых постоянная составляющая является параметром.

Определяется по соответствующей характеристике для мгновенных значений или экспериментально. Применяется при использовании метода расчета по первым гармоникам

Характеристика для действующих значений

Характеристика, связывающая действующие значения синусоидальных и несинусоидальных величин.

Определяется по соответствующей характеристике для мгновенных значений или экспериментально.

Применяется при использовании метода расчета по действующим значениям

Графические методы расчета

Графические методы расчета позволяют проводить анализ нелинейных цепей переменного тока для частных значений параметров с использованием характеристик нелинейных элементов для мгновенных значений, по первым гармоникам и действующим значениям (см. табл. 1).

Графический метод с использованием характеристик для мгновенных значений

В общем случае методика анализа нелинейной цепи данным методом включает в себя следующие этапы:

- исходя из физических соображений находят (если он не задан) закон изменения одной из величин, определяющих характеристику нелинейного элемента;

- по нелинейной характеристике для известного закона изменения переменной путем графических построений определяют кривую (или наоборот);

- с использованием полученной зависимости проводят анализ остальной (линейной) части цепи.

В качестве примера построим при синусоидальной ЭДС кривую тока в цепи на рис. 3, ВАХ диода в которой представлена на рис. 4.

1. Строим результирующую ВАХ цепи (см. рис. 4) согласно соотношению

2. Находя для различных значений с использованием полученной кривой соответствующие им значения тока, строим по точкам (см. рис. 5) кривую искомой зависимости .

К полученному результату необходимо сделать следующий комментарий. Использование при анализе подобных цепей ВАХ идеального вентиля (обратный ток отсутствует, в проводящем направлении падение напряжения на диоде равно нулю) корректно при достаточно больших значениях амплитуд приложенного к диоду напряжения , определяющих значительное превышение током, протекающим через вентиль в прямом направлении , его обратного тока , вследствие чего последним можно пренебречь. При снижении величин напряжения , когда эти токи становятся сопоставимыми по величине , следует использовать ВАХ реального диода , представленную на рис. 4 и учитывающую наличие обратного тока.

Важнейшим элементом в цепях переменного тока является катушка с ферромагнитным сердечником. В общем случае кривая зависимости имеет вид гистерезисной петли, но, поскольку в устройствах, работающих при переменном напряжении, используются магнитные материалы с узкой петлей гистерезиса, в большинстве практических случаев допустимо при расчетах использовать основную (или начальную) кривую намагничивания.

Условное изображение нелинейной катушки индуктивности приведено на рис. 6. Здесь – основной поток, замыкающийся по сердечнику, - поток рассеяния, которому в первом приближении можно поставить в соответствие потокосцепление рассеяния , где индуктивность рассеяния в силу прохождения потоком части пути по воздуху.

Для схемы на рис. 6 справедливо уравнение

В общем случае в силу нелинейности зависимости определить на основании (1) несинусоидальные зависимости и достаточно непросто. Вместе с тем для реальных катушек индуктивности падением напряжения и ЭДС, обусловленной потоками рассеивания, вследствие их малости, часто можно пренебречь. При этом из (1) получаем , откуда

где постоянная интегрирования.

Так как характеристика катушки (см. рис. 7) симметрична относительно начала координат , а напряжение симметрично относительно оси абсцисс (оси времени) , то кривая также должна быть симметричной относительно последней , откуда следует , что .

Находя для различных значений с использованием кривой соответствующие им значения тока , строим по точкам (см. рис. 7) кривую зависимости .

Анализ полученного результата позволяет сделать важный вывод: при синусоидальной форме потока напряжение на катушке синусоидально , а протекающий через нее ток имеет явно выраженную несинусоидальную форму. Аналогично можно показать , что при синусоидальном токе поток , сцепленный с катушкой , и напряжение на ней несинусоидальны.

Для среднего значения напряжения, наведенного потоком, можно записать

Умножив (2) на коэффициент формы, получим выражение для действующего значения напряжения

В частности, если напряжение и поток синусоидальны, то

Соотношение (2) является весьма важным: измеряя среднее значение напряжения, наведенного потоком, по (2) можно определить амплитуды потока и индукции при любой форме нелинейности катушки.

Аналогично проводится построение кривой при синусоидальном потоке и задании зависимости в виде петли гистерезиса. При этом следует помнить, что перемещение рабочей точки по петле осуществляется против часовой стрелки (см. рис. 8).

К полученному результату следует сделать следующий важный комментарий. Разложение построенной кривой в ряд Фурье показывает , что первая гармоника тока (см. кривую на рис. 8) опережает по фазе потокосцепление и , следовательно , отстает по фазе от синусоидального напряжения на катушке на угол, меньший 90 ° . Это указывает ( ) на потребление катушкой активной мощности , затрачиваемой на перемагничивание сердечника и определяемой площадью петли гистерезиса.

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.

Контрольные вопросы и задачи

В чем заключаются особенности нелинейных цепей переменного тока?
Какие типы характеристик используются в цепях переменного тока для описания нелинейных элементов?
В каких случаях допустимо использование при расчетах идеальных ВАХ вентилей?
Почему нельзя потокосцепление рассеяния катушки представить как произведение числа ее витков и потока рассеяния?
Как косвенным путем можно определить амплитуду индукции магнитного поля, сцепленного с катушкой?
Построить кривые и при синусоидальном токе в нелинейной катушке.
Почему первая гармоника разложения кривой тока при учете гистерезисной петли отстает от напряжения на угол, меньший 90 ° ?
Определить амплитуду основного рабочего потока в сердечнике нелинейной катушки сечением , если при числе витков среднее значение напряжения, обусловленного изменением потока, ; частота .

Название работы: Расчет нелинейных электрических цепей

Предметная область: Коммуникация, связь, радиоэлектроника и цифровые приборы

Описание: Если в сложной электрической цепи имеется одна ветвь с нелинейным резистором то определение тока в ней можно проводить на основе теоремы об активном двухполюснике методом эквивалентного генератора. Ветвь содержащая нелинейный резистор выделяется из исходной цепи а вся остальная уже линейная схема представляется в виде активного двухполюсника АД. Если необходимо также найти токи в линейной части исходной цепи то после расчета нелинейной схемы на рис. 1б в соответствии с теоремой о компенсации нелинейный резистор заменяется.

Дата добавления: 2013-10-22

Размер файла: 63.85 KB

Работу скачали: 39 чел.

Лекция 31_ Расчет нелинейных электрических цепей.

Если в сложной электрической цепи имеется одна ветвь с нелинейным резистором, то определение тока в ней можно проводить на основе теоремы об активном двухполюснике (методом эквивалентного генератора). Идея решения заключается в следующем. Ветвь, содержащая нелинейный резистор, выделяется из исходной цепи, а вся остальная, уже линейная, схема представляется в виде активного двухполюсника (АД). Согласно теореме об АД схему линейного АД по отношению к зажимам 1-2 выделенной ветви (см. рис. 1,а) можно представить эквивалентным генератором (см. рис. 1,б) с ЭДС, равной напряжению на зажимах 1-2 при разомкнутой ветви с нелинейным резистором, и внутренним сопротивлением, равным входному сопротивлению линейного двухполюсника. Последняя схема рассчитывается, например, графическим методом как цепь с последовательным соединением элементов.

Если необходимо также найти токи в линейной части исходной цепи, то после расчета нелинейной схемы на рис. 1,б в соответствии с теоремой о компенсации нелинейный резистор заменяется источником ЭДС или тока, после чего проводится анализ полученной линейной цепи любым известным методом.

Аналитические методы расчета

Исследования общих свойств нелинейных цепей удобно осуществлять на основе математического анализа, базирующегося на аналитическом выражении характеристик нелинейных элементов, т.е. их аппроксимации. На выбор аналитического метода влияют условия поставленной задачи, а также характер возможного перемещения рабочей точки по характеристике нелинейного элемента: по всей характеристике или в ее относительно небольшой области.

К аналитическим методам относятся:

метод аналитической аппроксимации;
метод кусочно-линейной аппроксимации;
метод линеаризации.

Метод аналитической аппроксимации основан на замене характеристики (или ее участка) нелинейного элемента общим аналитическим выражением. Применяются следующие виды аналитической аппроксимации:

степенным многочленом (см. рис. 2,а);
трансцендентными (экспоненциальными, гиперболическими и др.) функциями (см. рис. 2,б).

Выбор коэффициентов (а,b,c,…) осуществляется исходя из наибольшего соответствия аналитического выражения рабочему участку нелинейной характеристики. При этом

выбираются наиболее характерные точки, через которые должна пройти аналитическая кривая. Число точек равно числу коэффициентов в аналитическом выражении, что позволяет однозначно определить последнее.

Необходимо помнить, что при получении нескольких корней нелинейного уравнения они должны быть проверены на удовлетворение задаче. Пусть, например, в цепи, состоящей из последовательно соединенных линейного R и нелинейного резисторов, ВАХ последнего может быть аппроксимирована выражением . Определить ток в цепи, если источник ЭДС Е обеспечивает режим работы цепи в первом квадранте.

В соответствии со вторым законом Кирхгофа для данной цепи имеет место уравнение

Решением задачи является , поскольку второе решение не удовлетворяет условиям исходя из физических соображений.

Метод кусочно-линейной аппроксимации основан на представлении характеристики нелинейного элемента отрезками прямых линий (см. рис. 3), в результате чего нелинейная цепь может быть описана линейными уравнениями с постоянными (в пределах каждого отрезка) коэффициентами.

При наличии в цепи двух и более нелинейных резисторов реализация метода затруднена, так как в общем случае изначально неизвестно, на каких участках ломаных кривых находятся рабочие точки.

Кусочно-линейная аппроксимация может быть реализована методом секционных кусочно-линейных функций, позволяющим описать ломаную кривую общим аналитическим выражением. Например, для кривой, представленной на рис. 4 и определяемой коэффициентами и характеризующими наклон ее отдельных прямолинейных участков, и параметрами , характеризующими координаты точек, где значения функции изменяются скачками, данное выражение будет иметь вид

Здесь два первых слагаемых в правой части определяют первый наклонный участок аппроксимируемой кривой; три первых слагаемых - первый наклонный участок и участок первого скачка; четыре первых слагаемых - первый и второй наклонные участки с учетом участка первого скачка и т.д.

В общем случае аппроксимирующее выражение по методу секционных кусочно - линейных функций имеет вид

Метод линеаризации применим для анализа нелинейных цепей при малых отклонениях рабочей точки Р (см. рис. 5) от исходного состояния.

В окрестности рабочей точки (см. рис. 5)

где ( закон Ома для малых приращений );

-дифференциальное сопротивление.

Идея метода заключается в замене нелинейного резистора линейным с сопротивлением, равным дифференциальному в заданной (или предполагаемой) рабочей точке, и либо последовательно включенным с ним источником ЭДС, либо параллельно включенным источником тока. Таким образом, линеаризованной ВАХ (см. прямую на рис. 5) соответствует последовательная (рис. 6,а) или параллельная (рис. 6,б) схема замещения нелинейного резистора.

Если исходный режим определен и требуется рассчитать лишь приращения токов и (или) напряжений, обусловленные изменением напряжения или тока источника, целесообразно использовать эквивалентные схемы для приращений, получаемые на основании законов Кирхгофа для малых приращений:

-первый закон Кирхгофа: ;

-второй закон Кирхгофа: .

При составлении схемы для приращений:

1) все ЭДС и токи источников заменяются их приращениями;

2) нелинейные резисторы заменяются линейными с сопротивлениями, равными дифференциальным в рабочих точках.

Необходимо помнить, что полная величина какого-либо тока или напряжения в цепи равна алгебраической сумме исходного значения переменной и ее приращения, рассчитанного методом линеаризации.

Если исходный режим работы нелинейного резистора неизвестен, то следует задаться рабочей точкой на его ВАХ и, осуществив соответствующую линеаризацию, произвести расчет, по окончании которого необходимо проверить, соответствуют ли его результаты выбранной точке. В случае их несовпадения линеаризованный участок уточняется, расчет повторяется и так до получения требуемой сходимости

Итерационные методы расчета

Решение нелинейного уравнения (системы нелинейных уравнений), описывающего (описывающих) состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится следующим образом: на основе первой, достаточно грубой, оценки определяется начальное значение корня (корней), после чего производится уточнение по выбранному алгоритму до вхождения в область заданной погрешности.

Наиболее широкое применение в электротехнике для численного расчета нелинейных резистивных цепей получили метод простой итерации и метод Ньютона-Рафсона, основные сведения о которых приведены в табл. 1.

Таблица 1. Итерационные методы расчета

Геометрическая иллюстрация алгоритма

Условие сходимости итерации

Метод простой итерации

1.Исходное нелинейное уравнение электрической цепи , где -искомая переменная, представляется в виде .

2. Производится расчет по алгоритму где

Здесь - заданная погрешность

На интервале между приближенным и точным значениями корня должно выполняться неравенство

1.Начальное приближение обычно находится из уравнения при пренебрежении в нем нелинейными членами.

2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка

итерационные формулы имеют вид ;

3. При решении системы уравнений сходимость обычно проверяется в процессе итерации.

1. На основании исходного нелинейного уравнения электрической цепи , где -искомая переменная, записывается итерационная формула где - шаг итерации.

2.По полученной формуле проводится итерационный расчет

Здесь - заданная погрешность

На интервале между приближенным и точным значениями корня должны выполняться неравенства

Примечания п. 1,2 и 3 к методу простой итерации распространимы на метод Ньютона-Рафсона. При этом при решении системы 2-го порядка

Читайте также: