Метод штрафных функций реферат

Обновлено: 02.07.2024

Функцию удобно записать следующим образом:

где r – положительная величина.

Тогда функция принимает вид

Алгоритм метода штрафных функций

Пусть имеется следующая задача: Минимизировать при ограничениях ,.

Начальный этап Выбрать в качестве константы остановки, начальную допустимую точку ∈, для которой , , скаляр и . Положить k=1 и перейти к основному этапу.

Основной этап. k-я итерация.

Первый шаг. При исходной точке решить следующую задачу безусловной оптимизации:

- параметр, значения которого убывают с каждой итерации при ; - положительные весовые коэффициенты.

Примерами штрафных функций являются:

1) обратная функция

2) логарифмическая функция

Положить равным оптимальному решению задачи минимизации и перейти ко второму шагу.

Минимизация штрафной функцию может быть выполнена любым методом безусловной оптимизации, например, градиентным.

Если , то остановиться. Решение является искомым.

В противном случае положить . Изменить и перейти к первому шагу (k+1)-й итерации.

Метод барьерных функций

Изложение метода

Метод штрафных функций относится к группе методов внутренней точки, т.е. он начинает работать с допустимой точки и генерирует последовательность допустимых точек . Метод барьерных функций, наоборот, относится к группе методов внешней точки, он начинает поиск с недопустимой точки и генерирует последовательность недопустимых решений, которая приближается к оптимальному решению извне допустимой области.

Пусть имеется задача минимизировать при ограничениях

В частности, для искомых функций – ограничений целесообразно использовать барьерную функцию следующего вида:

- непрерывные функции, которые удовлетворяют условиям: , если и , если , , если и , если .

Типичными являются следующие выражения для функций :

, , где р – целое положительное число.

Далее от исходной задачи переходим к задачи безусловной оптимизации вспомогательной функции: минимизировать , где - штрафной коэффициент.

Пусть α– непрерывная функция. Обозначим .

Подход, связанный с барьерной функцией состоит в решении задачи вида:

максимизировать при ограничении

Алгоритм метода барьерных функций

Пусть имеется следующая задача:

Минимизировать при ограничениях ,, где функции .

Начальный этап Выбрать Выбрать начальную точку , параметр штрафа и число . Положить k=1 и перейти к основному этапу.

Основной этап. k-я итерация.

Первый шаг. При начальной точке и параметре штрафа решить следующую задачу:

Положить равным оптимальному решению задачи и перейти ко второму шагу.

Если , то остановиться.

В противном случае положить . Заменить k на k+1 и перейти к первому шагу.

Пример реализации

Рассмотрим задачу Розена-Сузуки и реализуем её решение с помощью метода штрафных функций. Задача Розена-Сузуки заключается в следующем: необходимо минимизировать функцию

со следующими ограничениями

Ниже приведена таблица промежуточных результатов алгоритма.

Число итераций	Значение миимизируемой функции	Координаты первой точки	Координаты второй точки	Координаты третьей точки	Координаты четвертой точки
0	nfmin=-43.739500	x1=-0.010000	x2=0.990000	x3=1.990000	x4=-0.990000
10	nfmin=-43.762449	x1=-0.009498	x2=0.990302	x3=1.991304	x4=-0.990502
20	nfmin=-43.785381	x1=-0.008996	x2=0.990604	x3=1.992607	x4=-0.991004
30	nfmin=-43.808298	x1=-0.008494	x2=0.990906	x3=1.993910	x4=-0.991506
40	nfmin=-43.831199	x1=-0.007993	x2=0.991208	x3=1.995212	x4=-0.992007
50	nfmin=-43.854084	x1=-0.007491	x2=0.991509	x3=1.996514	x4=-0.992509

Оптимальную точку мы получаем на 114й итерации с оптимальным значением функции

Основные понятия и определения нелинейного программирования, его функциональные особенности. Методы последовательной безусловной оптимизации и штрафных функций, их отличительные свойства. Решение задач методом штрафов, главные этапы данного процесса.

Рубрика	Программирование, компьютеры и кибернетика
Вид	курсовая работа
Язык	русский
Дата добавления	01.10.2012
Размер файла	1,4 M

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

В наиболее общем смысле теория оптимизации представляет собой совокупность фундаментальных математических результатов и численных методов, ориентированных на нахождение и идентификацию наилучших вариантов из множества альтернатив и позволяющих избежать полного перебора и оценивания возможных вариантов. Процесс оптимизации лежит в основе всей инженерной деятельности.

Важность и ценность теории оптимизации заключается в том, что она дает адекватные понятийные рамки для анализа и решения многочисленных задач:

? в исследовании операций: оптимизация технико-экономических систем, транспортные задачи, управление запасами и т.д.;

? в численном анализе: решение линейных и нелинейных систем, численные методы, включая методы конечных элементов и т.д.;

? в автоматике: распознавание образов, оптимальное управление, фильтрация, управление производством, робототехника и т.д.;

? в математической экономике: решение больших макроэкономических моделей, моделей предпринимательства, теория принятия решений и теория игр.

Наиболее распространенные задачи на практике - это оптимизационные задачи при наличии ограничений, то есть задачи поиска оптимального решения, удовлетворяющего некоторой системе ограничений. Существование эффективных алгоритмов решения безусловных задач оптимизации всегда толкает на попытку использования этих методов для решения условных задач после соответствующего преобразования условной задачи к некоторой эквивалентной ей безусловной задаче.

Помимо метода возможных направлений существуют иные методы поиска условного экстремума. Одним из них является метод штрафных функций.

Все методы штрафных функций, несмотря на различные схемы и варианты, имеют одну общую особенность: в них производится переход от задачи условной оптимизации к эквивалентной задаче или последовательности задач безусловной оптимизации. Преимущество, которое получаем в результате такого перехода к новой функции, достигается за счет применения более простых алгоритмов.

1. Общая постановка задач оптимизации. Основные понятия и определения

Постановка каждой задачи оптимизации включает в себя два объекта: множество допустимых решений и целевую функцию (функционал), которую следует минимизировать или максимизировать на указанном множестве. С этой общей точки зрения и рассматриваются различные классы экстремальных задач, составляющие предмет линейного, нелинейного, динамического программирования, вариационного исчисления и теории оптимального управления.

Математическое программирование в самом общем виде можно определить как задачу оптимизации с ограничениями в пространстве R n :

Функция f(x) называется целевой функцией (функцией качества, критерием оптимальности), а множество условий g_k(x), l_j(x) и x?D - ограничениями задачи.

Решением задачи (1.1) называют любой вектор x, удовлетворяющий ограничениям, т.е. пара (х * , f(х * )), включающая точку х * и значение целевой функции.

Оптимальным решением или глобальным экстремумом задачи (1.1) называют вектор x*, минимизирующий значение f(x) на множестве всех решений: f (x*) ? f(x) для всех x ?D.

Задача максимизации функции сводится к задаче поиска минимума функции F = - f(x).

Точка х * является локальным минимумом целевой функции, если в окрестности е этой функции в этой точке достигается ее наименьшее значение.

Значительный интерес представляет деление задач оптимизации по виду целевой функции и ограничений, поскольку специфические особенности тех или иных задач играют важную роль при разработке методов и их решений.

2. Нелинейное программирование

Ряд практических инженерных задач связан с оптимизацией при наличии некоторого количества ограничений на управляемые переменные. Такие ограничения существенно уменьшают размеры области, в которой проводится поиск экстремума. На первый взгляд может показаться, что уменьшение размеров области должно упростить процедуру поиска экстремума. Но, напротив, процесс оптимизации становится более сложным, т.к. установленные выше критерии оптимальности нельзя использовать при наличии ограничений. Может нарушаться даже основное условие - равенство нулю первой производной в стационарной точке. Например, безусловный min f (x) = (x ? 2) 2 имеет место при x*= 2 (т.е. ?f (x*) = 0). Но если задача решается с учетом ограничений x ? 4, то условный минимум достигается в точке x* = 4, где f (4) = 4 ? 0.

2.1 Методы последовательной безусловной оптимизации.

Методы, использующие преобразование задачи с ограничениями в последовательность задач без ограничений путем введения вспомогательных функций называются методами последовательной безусловной минимизации.

Основная идея методов этой группы состоит в том, чтобы аппроксимировать исходную задачу условной оптимизации некоторой вспомогательной задачей , решение которой менее сложно, чем решение исходной. Естественно, что ограничившись одной вспомогательной задачей, можно получить лишь приближенное решение.

2.2 Методы штрафных функций

Основная идея методов штрафных функций состоит в преобразовании задачи нелинейного программирования при наличии ограничений либо в одну (эквивалентную исходной) задачу без ограничений, либо в эквивалентную последовательность задач без ограничений.

f (x)>min, xR n , (2.1)

g_i(x) ? 0, i = 1, m (2.2)

h_l (x)=0, l = 1, p.

Предполагается, что точка x* является решением этой задачи, известно некоторое начальное приближение x 0 , возможно недопустимое, т.е. не удовлетворяющее отношениям (2.2). С помощью рассматриваемых далее алгоритмов в пространстве R n строится конечная последовательность точек x t , t = 0,1,…, k, которая начинается с заданной точки x 0 и заканчивается точкой x k , дающей наилучшее приближение к точке экстремума x* среди всех точек построенной последовательности. В качестве точек последовательности x t > берутся стационарные точки штрафной функции - целевой функции вспомогательной задачи безусловной минимизации.

Конкретные методы, основанные на указанной общей схеме, определяются видом штрафной функции, а также правилами, по которым производится пересчет штрафных параметров по окончании очередного цикла безусловной минимизации. Идея преобразования задачи с ограничениями в надлежащим образом построенную последовательность задач без ограничений представляется заманчивой, главным образом, в связи с наличием эффективных и надежных методов безусловной минимизации.

Рисунок 2.1 - Метод внутренних штрафов

Рисунок 2.2 - Метод внешних штрафов

В зависимости от того, являются ли элементы последовательности x t > допустимыми или недопустимыми точками, говорят соответственно о методах внутренней (рис. 2.1) или внешней точки (рис. 2.2) Иногда их называют методами внутреннего или внешнего штрафа. Методы внутренних штрафных функций называют также методами барьерных функций.

Понятие штрафных функций

Штрафная функция определяется выражением:

P (x, R) = f (x) + H (R, g(x), h(x)), (2.3)

где R - набор штрафных параметров,

H - штраф - функции R и ограничений,

H (R, g(x), h (x)) = R? (g(x), h(x)).

Выражение для штрафа H определяется таким образом, чтобы допустимые точки задачи имели преимущество перед недопустимыми в отношении безусловной минимизации штрафной функции.

Методы внутренней точки связаны с такими H, при которых стационарные точки функции P (x, R) оказываются заведомо допустимыми.

Эти методы называют также методами барьеров, поскольку здесь штраф как бы создает вдоль границы допустимой области S барьер из бесконечно больших значений функции P.

Методы штрафных функций представляют большой интерес лишь при выполнении следующих требований:

1) решения подзадач должны стремиться к решению задачи нелинейного программирования вида:

lim x t > x*, t >k t + 1 = F(R t ) должно быть простым.

В данной работе мы рассмотрим метод внешней точки (метод внешнего штрафа).

Основные типы внешних штрафов.

Квадратичный штраф используется для учета ограничений-равенств вида:

H = R·(h (x)) 2 . (2.4)

При минимизации этот штраф препятствует отклонению величины h(x) от нуля (как вправо, так и влево). Ниже будет видно, что при увеличении R

стационарная точка соответствующей штрафной функции P (x, R) приближается к точке x*, т.к. в пределе h(x k ) = 0. Поскольку допустимая область S определяется ограничением h(x) = 0, то в допустимой области значение штрафа H = 0, а вне допустимой области H > 0 и тем больше, чем дальше точка x t выйдет за пределы допустимой области и чем больше R.

Рис. 2.3 - Квадратичный штраф

Штраф типа квадрата срезки

Отметим, что H - внешний штраф, и стационарные точки функции P (x, R) могут оказаться недопустимыми. С другой стороны, недопустимые точки не создают в данном случае дополнительных сложностей по сравнению с допустимыми. Различие между ними состоит лишь в том, что в допустимых и граничных точках H = 0.

Достоинства: функция P (x, R) определена и непрерывна всюду. Вычисления проводятся с положительными R; после решения очередной задачи безусловной минимизации R увеличивается.

Выбор штрафного параметра

При практическом использовании любой из рассмотренных выше штрафных функций требуется выбрать начальное значение R и изменять его после решения каждой подзадачи безусловной минимизации с тем, чтобы обеспечить сходимость последовательности стационарных точек x t .

Значение R следует выбирать следующим образом: при использовании внешних штрафов при переходе от одной подзадачи к другой значение R должно увеличиваться.

При этом необходимо установить, как именно будет изменяться R при переходе от одной подзадачи к другой. Например, для обычного квадратичного штрафа, учитывающего ограничения равенства, целесообразно начинать с R = 0, т.е. безусловной минимизации функции, а затем последовательно увеличивать R на некоторое ДR. Вычислительные эксперименты показывают, что точно найденная стационарная точка x t (R) перемещается вдоль некоторой гладкой кривой к точке x*.

С другой стороны, пересчет параметра R, имеющий целью обеспечить сходимость метода, автоматически приводит к ухудшению обусловленности вспомогательных задач (появление овражной структуры штрафной функции). Во многих методах безусловной оптимизации используется матрица Гессе - ? 2 P (x, R). Показано, что часть собственных значений этой матрицы зависит от величины R. При этом обусловленность матрицы Гессе ? 2 P (x, R) неограниченно ухудшается, когда R>?. Тем самым усложняется процесс решения вспомогательных задач безусловной оптимизации.

Построение эффективных алгоритмов на основе метода штрафных функций не представляет особых трудностей. Приведем простейший алгоритм, в котором используется штрафная функция:

Шаг 1: задать значения n, m, p, е₁, е₂, е₃, x 0 , R 0 ,

где n - размерность вектора x;

m - число ограничений-неравенств;

p - число ограничений-равенств;

е₁ - параметр окончания одномерного поиска;

е₂ - параметр окончания процедуры безусловной минимизации;

е₃ ? параметр окончания работы алгоритма;

x 0 - начальное приближение для x*;

R 0 - начальный вектор штрафных параметров.

Шаг 2: Построить P (x, R) = f (x) + H (R, g(x), h(x)).

Шаг 3: Найти значение x t + 1 , доставляющее минимум функции P(x t + 1 , R t )

при фиксированном R t . В качестве начальной точки использовать x t , в качестве параметра окончания шага - константу е₂.

Шаг 4: Проверка выполнения условия:

|P (x t + 1 , R t )? P (x t , R t ? 1 )| ? е₃.

Да: положить x k = x t + 1 > конец.

Шаг 5: Положить R t + 1 = R t + ДR t в соответствии с используемым правилом пересчета n > Шаг 2.

При наличии ограничений в форме неравенств и равенств используют следующие штрафные функции:

Метод множителей

Ухудшение обусловленности вспомогательных подзадач в обычной схеме метода штрафных функций существенно ограничивает применимость метода. В ряде работ предложены непараметрические схемы метода штрафных функций (т.е. не используется штраф R). Рассмотрим один из этих случаев.

Функция Лагранжа в условиях оптимальности выглядит следующим образом:

где R - постоянный весовой (нормирующий) коэффициент (в принципе, R может зависеть от номера ограничения i, но не от номера итерации t);

- символ, обозначающий оператор срезки.

Параметры у_i и ф_i осуществляют сдвиг штрафных слагаемых и играют принципиально иную роль, чем R. Этот сдвиг итеративно уточняется, в результате чего процесс сходится к решению при не очень жестких требованиях к задаче.

Компоненты векторов у и ф меняются по ходу вычислений. Однако в процессе решения каждой вспомогательной подзадачи безусловной минимизации оба этих вектора остаются постоянными. При переходе от одной подзадачи к другой векторы пересчитываются по правилам, которые будут рассмотрены ниже.

Начальная точка x₀ не обязательно должна быть допустимой, а начальные значения у и ф удобно (но не обязательно) выбирать нулевыми.

Формулы пересчета у и ф

Обозначим: x t - точка минимума штрафной функции на t - ой итерации,

т.е. функции P (x, у, ф).

При переходе к (t +1) - ой итерации множители пересчитываются по формулам:

Вектор у не имеет положительных компонент из-за наличия в формуле оператора срезки (g_i (x) ? 0). Компоненты ф могут иметь любой знак.

Каждый из этих векторов определяет сдвиг аргумента соответствующего штрафа, причем формулы пересчета таковы, что в результате изменения сдвига при переходе к новой подзадаче штраф за нарушение ограничений возрастает и вследствие этого стационарные точки x t приближаются к допустимой области S.

Для контроля сходимости метода используют последовательности

x t ,у t , ф t , f (x t ), g (x t ), h (x t ).

Остановка основного процесса происходит, когда члены, по крайней мере, одной из последовательностей перестают изменяться при пересчете множителей и последующей безусловной минимизации.

Заметим, что градиент штрафной функции в результате безусловной минимизации должен обратиться в нуль.

Связь параметров у_i, ф_i с множителями Лагранжа.

Рассмотрим величины у k , g_i(x k ), ф k , h_l(x k ), предполагая, что они являются пределами соответствующих последовательностей. Из (2.10) видно, что ф k может существовать, если только h_l(x k ) = 0.

Аналогично, в силу (2.9) для существования предельных значений

у k и g_i(x k ) необходимо выполнение одного из следующих условий: либо

С учетом этого запишем выражение для градиента штрафной функции (2.8) в точке x k :

Первые три ограничения следуют из (2.12).

Отсюда мы видим, что соотношения (2.13) - (2.16) - это условия Куна-Таккера для точки x k . Таким образом, полученная предельная точка является точкой Куна-Таккера. Из (2.12) видно, что соответствующие значения множителей Лагранжа могут быть найдены по формулам:

то есть, по существу, без каких-либо дополнительных вычислений.

Недостатки: Элементы итерационной последовательности x t приближаются к x*, находясь почти всегда вне допустимой области отсутствие правила выбора R.

3. Решение задач методом штрафов

Найти минимум в задаче:

Для того чтобы ввести штрафную функцию, используем квадратичный штраф, т.к. ограничение задано в виде равенства:

P (x, R) = (x₁ - 4) 2 + (x₂ - 4) 2 + R·(x₁ + x₂ - 5) 2

Запишем уравнения, определяющие стационарную точку функции P (x, R):

Выразим x₁ и x₂ через R: вместо x₂ подставим в первое выражение x₁ (и сократим на 2):

Переходя к пределу, получим:

Таким образом, метод сходится к точке x* = [2,5; 2,5], тогда f (x*) = 2,25 + 2,25 = 4,5.

В таблице 1 приведены результаты расчетов при R = 0,0.1, 1, 10,100,1000 …и т.д. Подсчитаем первую строчку этой табл иц ы .

Метод штрафных функций является одним из наиболее простых и широко применяемых методов решения нелинейных задач оптимизации. Идея метода основана на преобразовании исходной задачи с ограничениями в одну или последовательность задач безусловной оптимизации. Суть такого преобразования заключается в следующем. С помощью функций, задающих ограничения, строится так называемый штраф, который добавляется к целевой функции исходной задачи так, чтобы нарушение какого-нибудь ограничений становилось невыгодным с точки зрения полученной задачи безусловной оптимизации.

Рассмотрим задачу определения максимального значения вогнутой функции

где g(x) – выпуклая функция.

В соответствии с идеей метода штрафных функции исходную задачу условной оптимизации преобразуем в задачу безусловной оптимизации

Штрафная функция H(x) определяется ограничениями исходной задачи и имеет вид

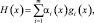
где параметры α_i(x) играют роль весовых коэффициентов. Излишне говорить, что штраф желателен только в недопустимых точках, поэтому

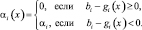
Процесс нахождения оптимального решения исходной задачи состоит в использовании штрафной функции для последовательного перехода из одной точки к другой, пока не получат приемлемое решение. Координаты последующей точки находят по формуле

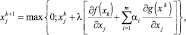
(5.18)

где λ ∈ [0; 1]. Из этого выражения следует, что если предыдущая точка находится в области допустимых решений исходной задачи, то второе слагаемое в квадратной скобке равна нулю и переход к последующей точке определяется только градиентом целевой функции. Если же эта точка не принадлежит области допустимых решений, то за счет этого слагаемого на последующих итерациях достигается возвращение в область допустимых решений. При этом чем меньше α_i, тем быстрее находится приемлемое решение, однако точность его определения снижается. Поэтому итерационный процесс обычно начинают при малых α_i и продолжая его α_i постепенно увеличивают.

Укрупненный алгоритм метода штрафных функций состоит из следующих шагов.

Шаг 0. Определение исходного допустимого решения.

Шаг 1. Выбирают шаг вычислений.

Шаг 2. Находят частные производные от целевой функции f(x) и функции g(x).

Шаг 3. По формуле (5.18) находят координаты точки, определяющей возможное новое решение задачи.

Шаг 4. Новую точку проверяют на допустимость по ограничениям исходной задачи. Если нет, то переход на шаг 5. При допустимости найденного решения исследуется необходимость перехода к следующему допустимому решению. При необходимости такого перехода возврат на шаг 1. В противном случае найдено приемлемое допустимое решение исходной задачи.

Шаг 5. Устанавливают значения α_i и переходят на шаг 3.

Пример 5.3. Необходимо максимизировать целевую функцию

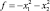
(5.19)

(x1 – 7) 2 + x2 – 7) 2 ≤ 18, x1, x2 ≥ 0. (5.20)

Решение. Целевая функция данной задачи – отрицательно-определенная квадратичная функция и, следовательно, вогнута, а область допустимых решений – выпукла. Следовательно, эта задача является задачей выпуклого программирования для уяснения процесса поиска оптимального решения дадим геометрическую интерпретацию этой задачи. Построим область допустимых решений (рис. 5.1), определяемой ограничениями (5.20) и линии уровня, определяемые целевой функцией (5.19). Этими линиями служат окружности с центром в точке (0; 0). Точка касания одной из этих окружностей с областью допустимых решений в виде круга с центром в точке Е и является искомой точкой максимального значения целевой функции.

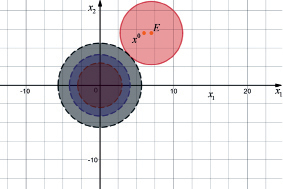
Рис. 5.1. Геометрическая интерпретация задачи

Для решения этой задачи воспользуемся методом штрафных функций.

Шаг 0. За исходное допустимое решение примем x 0 = (6; 7).

Шаг 1. Шаг вычислений выберем равным λ = 0,1.

Шаг 2. Представив функцию ограничения в виде

и определим частные производные от f(x) и g(x)

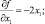
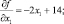
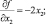
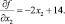
Теперь используя формулу (5.18) приступим к построению последовательности точек.

Шаг 3. Так как x0 = (6; 7) принадлежит области допустимых решений, то второе слагаемое в квадратной скобке формулы (5.18) равен нулю. Тогда координаты следующей точки x1 вычисляем по усеченной формуле (5.18)

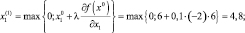
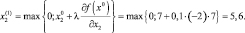
Шаг 4. Полученное решение проверяем на допустимость по ограничениям исходной задачи

g(x 1 ) = (4,8 – 7) 2 + (5,6 – 7) 2 = (–2,2) 2 + (–1,4) 2 = 6,8 2 ) = (3,84 – 7) 2 + (4,48 – 7) 2 18.

Итерация 4. Полученное на итерации 3 решение не является допустимой, поэтому для определения нового решения используем формулу (5.18) с учетом второго слагаемого квадратной скобки

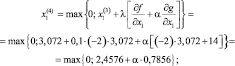
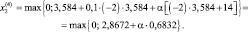
Здесь возникает вопрос о выборе числа α. Существует два подхода такого выбора. В первом случае надо взять значение α таким, чтобы точка x (4) не слишком далеко удалилась от границы области допустимых решений и вместе с тем принадлежала этой области. Такой достаточно произвольный выбор α зачастую увеличивает число итераций. Во втором случае используется формула Эрроу – Гурвица

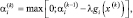
i = 1, …, m,

где в качестве начального значения α берут любое неотрицательное число.

Воспользуемся вторым подходом, тогда

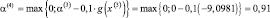
и по формуле (5.18) получим

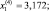
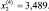
При этом g(x (4) ) ≈ –8,181.

Продолжая таким образом находим приемлемое решение, когда, либо ограничение будет выполняться почти как равенство, либо, когда значения целевой функции для соседних итераций будут отличаться между собой на незначительную величину.

В последние десятилетия появился ряд классов экстремальных задач, к которым классические методы решения, основанные на принципах Ферма и Лагранжа, оказались непосредственно неприменимыми. Такие задачи возникают в различных прикладных областях техники, экономики, экологии, и для них характерны ограничения не только типа равенств, но и неравенств, наличие большого числа переменных и ограничений, часто недифференцируемость целевых функций и функций ограничений, невыполнение условий регулярности, приводящее к вырожденным случаям и т.д.

Содержание

Введение
1. Общая задача нелинейного программирования
1.1 Постановка задачи
1.2 Теорема (обобщенное правило множителей Лагранжа)
1.3 Регулярный случай
1.4 Теорема (обобщенное правило множителей Лагранжа в регулярном случае)
1.5 Достаточные условия, существование, единственность
1.6 Об ограничениях-равенствах
1.7 Еще один достаточный признак условного минимума
2. Методы штрафных функций
2.1 Метод барьерных поверхностей
2.1.1 Алгоритм метода барьерных поверхностей
2.2 Метод штрафных функций
2.2.1 Алгоритм метода штрафных функций
Заключение
Список используемых источников

Работа состоит из 1 файл

Исследование методов штрафных функций (курсовая работа).docx

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального обучения

АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет математики и информатики

по курсу: Методы оптимизации

на тему: Исследование методов штрафных функций

Федеральное агентство по образованию Российской Федерации

Государственное образовательное учреждение высшего профессионального обучения

АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Факультет математики и информатики

к курсовой работе студентов

Тема работы: Исследование методов штрафных функций;
Срок сдачи студентами законченной работы: 15.12.2006 г.;
Дата выдачи задания: 01.09.2006 г.

Задание принял к исполнению 02.09.2006 г.

Курсовая работа, 26 страниц, 4 рисунков, 2 таблиц, 5 источников.

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНЕ, ОПТИМИЗАЦИЯ, ШТРАФ, БАРЬЕРНАЯ ФУНКЦИЯ, АЛГОРИТМ, МЕТОД, ИТЕРАЦИЯ

Объектом исследования являются методы штрафных функций.

Изучены методы и механизмы переход от задачи условной оптимизации к эквивалентной задаче или последовательности задач безусловной оптимизации.

По ходу исследования были решены некоторые примеры с помощью этих методов.

1. Общая задача нелинейного программирования

1.1 Постановка задачи

1.2 Теорема (обобщенное правило множителей Лагранжа)

1.3 Регулярный случай

1.4 Теорема (обобщенное правило множителей Лагранжа в регулярном случае)

1.5 Достаточные условия, существование, единственность

1.6 Об ограничениях-равенствах

1.7 Еще один достаточный признак условного минимума

2. Методы штрафных функций

2.1 Метод барьерных поверхностей

2.1.1 Алгоритм метода барьерных поверхностей

2.2 Метод штрафных функций

2.2.1 Алгоритм метода штрафных функций

Список используемых источников

Теоретически классические подходы могут быть распространены на некоторые классы таких задач, но часто они становятся малоэффективными или вообще практически неприменимыми. Поэтому появилась потребность в разработке новых идей и методов решения экстремальных задач, что привело к формированию нового раздела математики - математического программирования.

Методы штрафных функций, рассмотренные в этой работе, являются неотъемлемой частью курса математического программирования, и широко используются в силу своей простоты и эффективности.

1. Общая задача нелинейного программирования

1.1 Постановка задачи

Общей задачей нелинейной условной оптимизации мы будем называть условную задачу минимизации

f0(x) ® min, x Î W,(1.1)

где W выделяется как ограничениями типа равенств

fi(x) = 0, i = 1, . k,(1.2)

так и ограничениями типа неравенств

gj(x) £ 0, j = 1, . l(1.3)

Как и в предыдущем параграфе определяются допустимые точки , локальный и глобальный , строгий и нестрогий минимумы. Так же мы будем использовать обозначения f и g для функций из Rm в Rk и Rl, соответственно, определяемые координатами fi и gj. Поэтому задачу (1.1) – (1.3) можно записывать в виде

f0(x) ® min, f(x) = Q, g(x) £ Q.(1.4)

(напомним, что неравенство g(x) £ Q означает покоординатные неравенства).

Нам также потребуется следующее обозначение: a+ = (a + |a|)/2; таким образом, a+ = a, если a ³ 0 и a+ = 0, если a £ 0. Для векторов a Î Rm операция "+" определяется покоординатно: a+ = ((a1)+, . (am)+). Кроме того, через J(x) будет обозначаться множество индексов так называемых активных ограничений: J(x) = : gj(x) = 0> — это номера ограничений, которые в данной точке существенны. Например, на рисунке 1 J(x1) = , а J(x2) = Æ.

1.2 Теорема (обобщенное правило множителей Лагранжа)

Пусть f0, f, g Î C1, а x* — локальное решение задачи (1. 4 ). Тогда найдутся такие l*0 Î R, l* Î Rk, m* Î Rl, не равные одновременно нулю, такие, что m*j ³ 0 при j Î J(x*) и

Доказательство. Возьмем r > 0 таким, чтобы x* = argminxÎWr f(x), где Wr = W Ç B(x*, r) . Для любого n Î N определим функцию f n: Rm ® R равенством

Задача 1. Докажите, что f n Î C1, в частности, покажите, что (||g+(x)||2)¢ = 2g+(x)g¢(x).

Поскольку f n непрерывно дифференцируемы и поэтому непрерывны, функции f n на шаре B(x*, r) достигают минимума; обозначим его через xn. В частности,

Отсюда, поскольку, как легко видеть, f n(x*) = f0(x*),

ыражение в квадратных скобках ограничено, так как xn Î B(x*, r) . Поэтому ||f(xn)||2 + ||g+(xn)||2 ® 0 при n ® ¥ и, следовательно, f(xn) ® Q и g+(xn) ® Q при n ® ¥.

Пусть теперь — произвольная сходящаяся, скажем к y, подпоследовательность. Тогда, как легко видеть, во-первых, y Î W и, во-вторых, f ni(xni) ® f0(y) + ||y - x*||2 при n ® ¥. Поэтому, подставляя в (1.6) ni вместо n и переходя к пределу в получившемся неравенстве при i ® ¥, получим

С другой стороны, так как x* = argmin f(x), f0(x*) £ f0(y). Отсюда ||y - x*||2 £ 0, т. е. y = x*. Таким образом, любая сходящаяся подпоследовательность последовательности сходится к x*. Последнее, учитывая компактность последовательности, гарантирует ее сходимость к тому же пределу.

Далее, в силу доказанного можно считать, что при всех n точка xn лежит внутри шара B(x*, r) . Поэтому в силу теоремы Ферма (f n)¢(xn) = Q , т. е.

ln0 = sn, lni= 2nfi(xn)sn, mnj= 2n[gj(xn)]+sn. Поскольку ln0,lnj,mnjÎ [-1, 1] (n Î N; i = 1, . k; j = 1, . l), можно считать, не ограничивая общности, что найдутся такие l*0,l*iи m*j, что

ln0® l*0, lni® l*i, mnj® m*j при n ® ¥.

Умножив (1.7) на sn и переходя в получившемся равенстве к пределу при n ® ¥, получаем

Остается заметить, что, во-первых, так как |ln0|2+ åki=1|lni |2+ålj=1|mnj|2=1, не все из l*0,l*i,m*jравны нулю, во-вторых, поскольку mnj= 2n[gj(xn)]+sn ³ 0, неотрицательны и m*jи, наконец, в-третьих, если j Ï J(x*) (т. е. gj(x*)

Таким образом (1.8) — это (1.5) .

1.3 Регулярный случай

Так же, как и в случае ограничений-равенств в случае общей задачи нелинейной оптимизации , необходимый признак, информативен только в случае, если l*0¹ 0. В этой ситуации, так же как и в предыдущем параграфе можно разделить (1.5) на l*0 и, следовательно, считать его равным единице. Это позволяет ввести функцию Лагранжа L: Rm×Rk×Rk ® R (в регулярном случае) равенством

L(x, l, m) = f0(x) + (l, f(x)) + (m, g(x)).

Условие регулярности в случае общей задачи выглядит сложнее. Именно, допустимая точка x называется регулярной, если векторы f ¢1(x). f ¢k(x)линейно независимы и для некоторого ненулевого вектора h Î Rm

(f ¢i(x),h) = 0 при i = 1, . k

Геометрически, эти условия означают, что, во-первых, вектор h является касательным к многообразию, выделяемому ограничениями-равенствами (т. е. ортогонален всем градиентам f ¢i(x)),и, во-вторых, он образует с градиентами g¢j(x)активных ограничений (указывающими, очевидно, вовне множества W) тупой угол (рисунок 2).

1.4 Теорема (обобщенное правило множителей Лагранжа в регулярном случае).

Пусть f0, f, g Î C1, а x* — регулярное локальное решение задачи (1. 4 ). Тогда найдутся l* Î Rk, m* Î Rl не равные одновременно нулю, такие, что m*j ³ 0 при j Î J(x*) и

Доказательство. Пусть l0**, l** и m** — величины, существование которых утверждается в теореме 1. 2. Покажем, что l0** ¹ 0. В предположении противного умножим (1.5) скалярно на вектор h, фигурирующий в определении регулярности x*:

Рассматриваются основные теоретические положения метода штрафных функций.

Применение метода штрафов описывается на примере семи основных наиболее

часто применяемых штрафных функций. Приведены некоторые оценки сходимости

этих функций, а также вычислительные аспекты данного метода.

Написана программа, позволяющая эффективно решать задачи выпуклого

программирования методом штрафных функций с помощью ЭВМ.

Ключевые слова: оптимизационная задача, выпуклое программирование,

штрафная функция, глобальный минимум, релаксационный метод.

Объем пояснительной записки 24 страницы.

Использовано 7 источников литературы.

1. Постановка задачи выпуклого программирования 7

2. Теоретические положения метода штрафных функций 8

2.1 Метод штрафных функций 8

2.2 Характеристические свойства штрафных функций 8

2.3 Поиск локальных экстремумов 11

2.4 Сходимость метода штрафов 13

3. Реализация метода штрафов на ЭВМ 17

Список литературы 20

Приложение 1. Текст программы 21

Приложение 2. Результаты работы программы 24

Интенсивное развитие методов математического программирования связано с

тем, что оптимизационные задачи играют большую роль в самых различных

областях человеческой деятельности. Сейчас основное внимание уделяется

развитию методов выпуклого программирования. Построен целый ряд

алгоритмов, проведены исследования их сходимости. Однако эти алгоритмы

применяются довольно редко, и нет достаточной информации, позволяющей

судить об их сравнительной эффективности. При использовании методов

выпуклого программирования решение исходной задачи обычно определяется как

предел минимизирующей последовательности решений более простых (

вспомогательных ) экстремальных задач. Полагая в основу тип

вспомогательных задач, большинство методов выпуклого программирования

можно разделить на две группы.

* К первой группе относятся методы, при реализации которых на каждом

шаге приходится решать задачу минимизации линейной или выпуклой

функции при линейных ограничениях. Это различные варианты метода

возможных направлений (метод отсечения, проекций градиента ).

* Ко второй группе относятся методы, с помощью которых искомое решение

определяется как предел последовательности безусловных минимумов

специальным образом сконструированных вспомогательных функций: методы

штрафных функций, центров, множителей Лагранжа.

Первые оценки сходимости метода штрафных функций были получены Л. Битнером

и И.И. Бреминым, установившими оценки сходимости логарифмического и

квадратичного штрафов для решения задач выпуклого программирования. Б.Т.

Поляком получены оценки быстроты сходимости метода штрафов в окрестности

локального экстремума для выпуклых задач с ограничениями в форме

1. Постановка задачи выпуклого программирования.

Задачей выпуклого программирования будем называть задачу:

Если f(x) - выпуклая функция, а G - выпуклое множество, обычно G задается

где 0x01 graphic

- заданные выпуклые функции.

Теорема 1.1.0x01 graphic

Пусть f(x) - выпуклая функция, заданная на выпуклом замкнутом множестве D,

тогда любой локальный минимум f(x) на множестве D является глобальным.

Следствие. Если f(x) - строго выпуклая функция, то ее глобальный минимум

на выпуклом замкнутом множестве D достигается в единственной точке.

Легко видеть, что в задаче выпуклого программирования не существует

локальных минимумов со значением функции f большим, чем 0x01 graphic

а множество точек

является выпуклым и замкнутым.

2. Теоретические положения метода штрафных функций.

2.1. Метод штрафных функций.

Метод штрафных функций сводит задачу выпуклого программирования точно или

приближенно к задаче минимизации некоторой функции, представляющей собой

сумму данной целевой функции невязок в ограничениях задачи.

Пусть дана задача выпуклого программирования (1.1) - (1.2). Вводится

вспомогательная функция 0x01 graphic

где 0x01 graphic

- некоторый векторный параметр.

Функцию 0x01 graphic

называют штрафной функцией, если она обладает следующими свойствами:

т.е. при больших 0x01 graphic

функция 0x01 graphic

в области допустимых решений D близка f(x), а вне области D принимает

значения порядка +0x01 graphic

2.2. Характеристические свойства штрафных функций.

Хотя значительная часть приведенных ниже теоретических результатов о

характеристике штрафных функций и сходимости метода не зависит от того,

как задано множество G, способ задания множества G весьма важен как для

конкретного построения штрафных функций, так и для исследования их

свойств, связанных с соотношениями двойственности. Обычно, когда речь идет

о численных методах выпуклого программирования, предполагается, что

где 0x01 graphic

- выпуклая вектор - функция,

Будем рассматривать функции 0x01 graphic

В этом случае удобно проводить исследование свойств систем функций 0x01

на языке порождающих их функций одной переменной 0x01 graphic

Мы ограничимся рассмотрением нескольких порождающих функций, наиболее

часто употребляемых на практике:

Предполагается во всех случаях, что 0x01 graphic

Для краткости условимся обозначать номерами с (1) по (7) функции штрафа

Vk,, порожденные соответственно функциями (2.2.1) - (2.2.7).

Отметим, что при использовании второй из этих функций для минимизации

можно применять градиентные методы. Однако скорость сходимости этих

методов при больших значениях 0x01 graphic

медленная. При использовании функций (7) и (6) требуется определять

предварительную точку 0x01 graphic

, что несущественно, если используются функции (1) - (3) и (5).

Кроме того, необходимо, чтобы используемый метод минимизации

вспомогательной функции был релаксационным и полностью определялся

информацией о функциях 0x01 graphic

в int G. Иначе говоря, требуется некоторая модификация методов безусловной

Такие проблемы не возникают при использовании штрафных функций (1) - (3) и

(5). С другой стороны, как показывают теоретические исследования и анализ

экспериментов, функции (6) и (7) оказываются предпочтительнее, чем (2), с

точки зрения быстроты сходимости процесса. Использование функций (1) - (3)

существенно ограничивает возможности эффективного решения вспомогательных

задач, так как эти функции не обладают гладкостью, достаточной для

применения процедур безусловной минимизации высокого порядка.

В предположении, что 0x01 graphic

- возрастающая последовательность и вспомогательные задачи решаются точно,

применение штрафных функций (1), (2), (4) и (5) гарантирует монотонность

последовательностей 0x01 graphic

, где 0x01 graphic

, если Vk имеет вид (1), (2) или 0x01 graphic

, для функций (6) и (7). Это учитывается при изменении параметра 0x01

. Порождающие функции (2) и (3) являются аналитическими, и их применение

не ограничивает гладкости 0x01 graphic

на всем Rn . Штрафная функция (3) обладает относительно малым порядком

роста вне допустимой области, что избавляет о необходимости заботиться о

хорошем начальном приближении 0x01 graphic

Конечно, отмеченные выше особенности различных функций штрафа не дают

достаточных оснований предпочесть одну функцию другой, а, скорее,

позволяют построить гипотеза о предпочтении, для проверки которых

потребуются более тщательные исследования (априорные оценки, рекомендации

по выбору параметров 0x01 graphic

и т.д.) и прежде всего большой численный эксперимент.

2.3. Поиск локальных экстремумов.

Как уже отмечалось, решение невыпуклых экстремальных задач встречает

серьезные трудности, связанные с отсутствием удовлетворительных методов

безусловной минимизации невыпуклых функций. При реализации метода штрафных

функций на каждом шаге ограничиваемся отысканием некоторых локальных

экстремумов вспомогательных функций. При этом выбор локальных минимумов во

вспомогательных задачах должен быть организован так, чтобы любая их

предельная точка являлась локальным минимумом в исходной задаче (нетрудно

привести пример, показывающий, что этим свойством обладает не каждая

последовательность локальных минимумов, даже если ее предельные точки

Обозначим через А* множество таких локальных минимумов функции f на G, что

для 0x01 graphic

Теорема 2.1. Пусть А* - непустой компакт, 0x01 graphic

; S - компакт такой, что 0x01 graphic

для 0x01 graphic

; точки 0x01 graphic

выбираются из условий 0x01 graphic

где 0x01 graphic

Тогда начиная с некоторого номера, 0x01 graphic

и любая предельная точка последовательности 0x01 graphic

Доказательство. Существование точек 0x01 graphic

легко получить, применяя следующее утверждение:

Утверждение. Пусть 0x01 graphic

- непрерывная функция, 0x01 graphic

- компакт и существует такая точка x0x01 graphic

,что 0x01 graphic

. Тогда найдется точка 0x01 graphic

, для которой 0x01 graphic

. Любая предельная точка последовательности 0x01 graphic

принадлежит А*0x01 graphic

, причем А*0x01 graphic

совпадает с множеством 0x01 graphic

. Так как 0x01 graphic

, для больших k имеем 0x01 graphic

Отметим, что существование компакта S с указанными свойствами вытекает из

Лемма 2.1. Пусть f - непрерывная функция, G - замкнутое множество, А* -

непустой компакт. Тогда существует компакт S такой, что 0x01 graphic

для 0x01 graphic

Доказательство. Рассмотрим последовательность компактов 0x01 graphic

. Легко проверить, что 0x01 graphic

. Если утверждение леммы неверно, то при каждом k найдется точка 0x01

такая, что 0x01 graphic

. Не умаляя общности, можно считать, что 0x01 graphic

. Точка 0x01 graphic

при этом должна принадлежать А*0x01 graphic

. Если 0x01 graphic

при всех k, то 0x01 graphic

не может быть локальным минимумом, вопреки определению А*. Если же 0x01

при некотором k, то из соотношения

следует, что 0x01 graphic

, причем 0x01 graphic

содержится в 0x01 graphic

вместе с некоторой окрестностью 0x01 graphic

, так что 0x01 graphic

. Тем самым 0x01 graphic

- локальный минимум функции f на G и 0x01 graphic

, что противоречит выбору последовательности 0x01 graphic

Мы рассмотрели случаи, когда ограничения в задаче в виде неравенств. Когда

среди ограничений задачи имеются равенства, применяют штрафную функцию,

порождаемую 0x01 graphic

. Отметим, что учет ограничения 0x01 graphic

с помощью этой функции то же самое, что и учет эквивалентной пары

ограничений 0x01 graphic

с помощью функции (3).

2.4. Сходимость метода штрафов.

Метод штрафных функций является двухступенчатым итерационным процессом в

том смысле, что для отыскания каждой точки последовательности 0x01 graphic

, как правило, приходится применять какой - либо бесконечношаговый метод

Скорость сходимости метода штрафов естественно оценивать числом больших

штрафов, каждый из которых состоит в отыскании очередной точки 0x01

. Такая оценка, с одной стороны, не зависит от выбора алгоритма решения

вспомогательной задачи. С другой стороны, с ее помощью нетрудно получить

оценку числа малых шагов, если, конечно, известна скорость сходимости

выбранного алгоритма безусловной минимизации.

Следует отметить, что метод штрафов не вполне отвечает обычным

представлениям об итерационных процессах: множество 0x01 graphic

точек 0x01 graphic

, которые могут быть получены на k-ом шаге, не зависит от выбора 0x01

. Тем самым оценка величин 0x01 graphic

, где 0x01 graphic

, не должна зависеть ни от начальной точки 0x01 graphic

, ни от результата предыдущих итераций.

Получим некоторые априорные оценки быстроты сходимости метода штрафов при

решении задач выпуклого программирования.

Определим систему функций 0x01 graphic

- выпуклая функция, 0x01 graphic

для всех 0x01 graphic

c) известна функция 0x01 graphic

такая, что 0x01 graphic

, причем 0x01 graphic

e) известна функция 0x01 graphic

такая, что при любом 0x01 graphic

для 0x01 graphic

справедливо неравенство 0x01 graphic

, причем 0x01 graphic

Рассмотрим теперь систему функций 0x01 graphic

где 0x01 graphic

удовлетворяют условиям a) - e) (будем при этом говорить, что система 0x01

обладает 0x01 graphic

- свойством). Нетрудно проверить, что система функций (2.4.1)

удовлетворяет следующему утверждению.

Утверждение. Пусть в задаче выпуклого программирования (1.1) - (1.2)

множество G телесно, 0x01 graphic

не пусто и ограничено, функции 0x01 graphic

выпуклы и удовлетворяют условию

Тогда, начиная с некоторого k, существуют точки 0x01 graphic

, удовлетворяющие неравенству 0x01 graphic

для всех 0x01 graphic

; последовательность 0x01 graphic

ограничена, любая ее предельная точка 0x01 graphic

принадлежит G и

Теорема 2.2. Пусть f сильно выпукла с константой 0x01 graphic

и для решения задачи выпуклого программирования применяется метод штрафов

с градиентным критерием остановки, 0x01 graphic

Тогда если функции штрафа обладают 0x01 graphic

- свойством, то существуют такие 0x01 graphic

при 0x01 graphic

, где 0x01 graphic

- число элементов в множествах 0x01 graphic

соответственно, 0x01 graphic

Отметим, что неравенства (2.4.2), (2.4.3) не содержат 0x01 graphic

, однако от выбора последовательности 0x01 graphic

зависят величины 0x01 graphic

Среди рассмотренных нами систем функций штрафа 0x01 graphic

- свойством обладает лишь система (5) при 0x01 graphic

Аналогично могут быть установлены оценки быстроты сходимости метода при

некоторых других функциях штрафа. Так, если 0x01 graphic

, при использовании функции (6) в тех же условиях имеем неравенство

а если взять 0x01 graphic

, то в случае функции (4) получим

Эти оценки улучшаемы по порядку в данном классе задач.

Если известны удовлетворительные приближения для оптимальных множителей

Лагранжа, то оценки быстроты сходимости метода штрафов можно получить с

помощью решения достаточно простых вспомогательных экстремальных задач.

3. Реализация метода штрафов на ЭВМ.

Для решения задач выпуклого программирования на ЭВМ удобно использовать

метод обобщенного градиента, согласно которому точка 0x01 graphic

получается как предел последовательности точек

где 0x01 graphic

- числовой параметр, 0x01 graphic

- значение в точке 0x01 graphic

обобщенного градиента функции 0x01 graphic

, определяемого следующим образом:

Таким образом, если 0x01 graphic

, то 0x01 graphic

, т.е., получаем обычный метод градиента для функции 0x01 graphic

. Если 0x01 graphic

, то обобщенный градиент представляет собой линейную комбинацию градиентов

целевой функции 0x01 graphic

и функций, соответствующих тем ограничениям, которые не выполняются в

Для примера реализуем на ЭВМ решение задачи Розена - Сузуки методом

Задача Розена - Сузуки:

при следующих ограничениях:

Оптимальным решением этой задачи является

Будем решать эту задачу методом штрафных функций, а полученную задачу

минимизации методом обобщенного градиента.

В качестве параметров, выберем 0x01 graphic

Программа написана на языке С++.

В данной работе были рассмотрены основные теоретические положения метода

штрафных функций, получены некоторые оценки сходимости для наиболее

употребляемых штрафных функций, а также их характеристические свойства.

Результатом работы является программа на языке С++, решающая методом

штрафных функций задачи выпуклого программирования, и, в частности, задачу

Читайте также:

Метод штрафных функций реферат

Алгоритм метода штрафных функций

Метод барьерных функций

Изложение метода

Алгоритм метода барьерных функций

Пример реализации

Рекомендация программисту

Содержание

Работа состоит из 1 файл

Исследование методов штрафных функций (курсовая работа).docx