Линейный интеграл в векторном поле реферат

Обновлено: 04.07.2024

Пусть поле - непрерывное векторное поле, (L) – кусочно гладкая кривая с выбранным на ней положительным направлением (ориентированная кривая).

Определение 1. Линейным интегралом (обозначается L) вектора вдоль ориентированной кривой (L) называется криволинейный интеграл

Для линейного интеграла справедливы следующие формулы:

Если поле есть силовое поле , то линейный интеграл (1.7) дает величину работы этого поля вдоль линии (L). Вычисление линейного интеграла в зависимости от задачи может быть проведено по одной из формул “списка” (1.8).

Определение 2. Циркуляцией (обозначается Ц) векторного поля называется линейный интеграл по замкнутой ориентированной кривой (L):

За положительное направление обхода замкнутой кривой (L) берется то, при котором область, ограниченная кривой, лежит под левой рукой.

Пример 1. Найти линейный интеграл вектора вдоль дуги (L) винтовой линии от точки A пересечения линии с плоскостью Z=0 до точки В пересечения с плоскостью Z =1.

Решение. Имеем по последней формуле из списка (1.8): . Точке A соответствует значение параметра T =0, точке B – значение и, таким образом, .

Пример 2. Вычислить работу силового поля вдоль отрезка прямой, проходящей через точки и .

Запишем канонические уравнения прямой .
Отсюда ; параметры . Вычислим работу:
.

Пример 3. Вычислить циркуляцию поля вдоль эллипса .

Решение. Имеем по формуле (1.9) и (1.8): .
Запишем параметрические уравнения эллипса: . Вычисляя Dx и Dy, получим: - здесь использовано, что (вычисление этих интегралов проводится с помощью понижения степени подынтегральной функции).

Пример 4. Вычислить циркуляцию векторного поля вдоль линии L, полученной пересечением конуса с координатными плоскостями (см. рис.4).

Пример 5. Вычислить циркуляцию векторного поля вдоль линии , .

Решение. Имеем: . Линия L есть эллипс, получающийся в результате сечения цилиндра плоскостью . Найдем параметрические уравнения этой линии. Проекция любой точки этой линии на плоскость Oxy находится на окружности . Отсюда, полагая , найдем, что . Для Z из уравнения получим: . Таким образом, . Находим отсюда: , и для циркуляции запишем определенный интеграл: .

Пусть в пространственной области $\mathbf < \textit < V >> $ определено непрерывное векторное поле $\bar < a >(\mathbf < \textit < M >> ), \mathbf < \textit < L >> $ - гладкая кривая, расположенная в $\mathbf < \textit < V >> $. Линейным интегралом поля $\bar < a >$ вдоль линии $\mathbf < \textit < L >> $ называется криволинейный интеграл по длине дуги от скалярного произведения $\bar < a >(\mathbf < \textit < M >> )$ на единичный касательный вектор $\bar < \tau >(\mathbf < \textit < M >> ): W=\int\limits_L < \bar < a >(M)\cdot \bar < \tau >(M)\,ds > $.

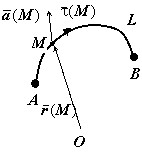
Как и поток, этот интеграл может представляться различным образом. Так, если учесть, что произведение $\bar < \tau >(M)$ на $ds$ даёт изменение радиуса-вектора точки $\mathbf < \textit < M >> $, т.е. $\bar < \tau >\cdot ds=d\bar < r >=dx\bar < i >+dy\bar < j >+dz\bar < k >$,то $W=\int\limits_L < \bar < a >(M)d\bar < r >> $ и $W=\int\limits_L < Pdx+Qdy+Rdz >$. Следовательно, линейный интеграл может быть выражен и через линейный интеграл по координатам.

Физический смысл линейного интеграла:

если $\bar < a >(\mathbf < \textit < M >> )$ - силовое поле, то $W$ равен работе этого поля при перемещении материальной точки вдоль линии $\mathbf < \textit < L >> $ см. раздел Тройные интегралы.

Основные свойства линейного интеграла.

1). Линейность

$\int\limits_L < \left( < С_1 \bar < a >_1 +С_2 \bar < a >_2 >\right)\bar < \tau >\,ds > =С_1 \int\limits_L < \bar < a >_1 \bar < \tau >\,ds > +С_2 \int\limits_L < \bar < a >_2 \bar < \tau >\,ds > $,

2). Аддитивность

$\int\limits_ < L_1 \cup L_2 > < \bar < a >\cdot \bar < \tau >\,ds > =\int\limits_ < L_1 > < \bar < a >\cdot \bar < \tau >\,ds > +\int\limits_ < L_2 > < \bar < a >\cdot \bar < \tau >\,ds > $. Направление на каждой из частей $\mathbf < \textit < L >> _ < 1 >$ и $\mathbf < \textit < L >> _ < 2 >$ должно быть таким же, как и на всей кривой $L_1 \cup L_2 $,

3). При изменении направления вдоль $\mathbf < \textit < L >> $ линейный интеграл меняет знак.

Это следует из того, что вектор $\bar < \tau >(\mathbf < \textit < M >> )$ меняется на - $\bar < \tau >(\mathbf < \textit < M >> )$.

4). Если $\mathbf < \textit < L >> $ - векторная линия поля и движение происходит в направлении поля, то $\mathbf < \textit < W >> >0$. В этом случае вектор $\bar < \tau >(\mathbf < \textit < M >> )$ коллинеарен $\bar < a >(\mathbf < \textit < M >> )$, поэтому $\bar < a >\cdot \bar < \tau >=\mathop < \mbox < пр >\bar < a >> \limits_ < \bar < \tau >> =\vert \bar < a >\vert >0$.

Вычисление линейного интеграла

Как и любой криволинейный интеграл, линейный интеграл вычисляется сведением к определённому интегралу по параметру на кривой, обычно вычисляют криволинейный интеграл $W=\int\limits_L < Pdx+Qdy+Rdz >$. Если кривая при параметрическом задании имеет вид $L:\left\ < < \begin < l >x=x(t), \\ y=y(t), \\ z=z(t), \\ \end >\right. t_0 \leqslant t\leqslant t_k $, где $x(t),\,y(t),\,z(t)$- непрерывно дифференцируемые функции, то $W=\int\limits_L < P(x,y,z)\cdot dx+Q(x,y,z)\cdot dt+R(x,y,z)\cdot dz >= \\ =\int\limits_ < t_0 >^ < t_k > < \left[ < P(x(t),y(t),z(t))\cdot < x >'(t)+Q(x(t),y(t),z(t))\cdot < y >'(t)+R(x(t),y(t),z(t))\cdot < z >'(t) >\right]dt > .$

Направление интегрирования определяется направлением движения по кривой.

Циркуляция векторного поля

Циркуляцией называется линейный интеграл векторного поля по замкнутой кривой $\mathbf < \textit < C >> $: Ц$=\oint\limits_C < \bar < a >\cdot d\bar < r >> $.

Обычно говорят, что циркуляция характеризует вращательную способность поля. Имеется в виду следующее. Если векторные линии поля замкнуты, то, как мы видели, циркуляция по ним в направлении поля положительна, при этом в гидродинамической интерпретации частицы жидкости крутятся по этим замкнутым линиям. Пусть теперь линии тока произвольны, вообразим в объёме $\mathbf < \textit < V >> $ замкнутый контур $\mathbf < \textit < C >> $. Если в результате движения жидкости этот контур будет вращаться, то поле обладает вращательной способностью, абсолютная величина циркуляции будет определять угловую скорость вращения < чем больше $\vert$ Ц $\vert $, тем выше скорость > , знак циркуляции покажет, совпадает ли направление вращения с направлением интегрирования.

Класс $L$. Теорема о замкнyтости класса $L$

Функции k-значной логики. Элементарные функции. Лемма об аналоге правила де Моргана

Вычисление криволинейного интеграла второго рода. Примеры.

Определение тройного интеграла. Теорема существования тройного интеграла

Поверхностный интеграл второго рода и его свойства

Примеры применения цилиндрических и сферических координат

Вычисление площади поверхности

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Пусть задано поле сил , под действием которых материальная точка движется по кривой от точки к точке . Вычислим совершаемую при этом работу. Для этого разобьем линию на частей точками с радиус-векторами (рис. 66). Рассмотрим вектор перемещения

и вектор силы . Их скалярное произведение приближенно равно работе силы вдоль дуги , т. е.

Вычислим работу вдоль всей линии :

Это равенство будет тем точнее, чем меньше длины векторов . Максимальную из этих длин обозначим и, переходя к пределу при , определим точное значение работы

Этот предел обозначают и называют линейным интегралом поля по дуге или криволинейным интегралом второго рода.

Отвлекаясь от физического содержания рассмотренной задачи, аналогичным образом вводят понятие линейного интеграла произвольного поля (риc. 4):

где ─ точки разбиения дуги , .

Отметим три свойства линейного интеграла:

1) (свойство линейности),

2) (свойство аддитивности),

т. е. при изменении направления обхода кривой линейный интеграл меняет знак, т. к. векторы меняют свое направление на противоположное.

Выразив скалярное произведение векторов и через их координаты, получим

Выражение в скобки не заключают, хотя знак интеграла относится ко всему этому выражению. В формуле функции есть функции точки или ее координат . Интеграл называют векторной формой, а интеграл ─ координатной формой записи линейного интеграла.

В тех случаях, когда линейный интеграл поля берется по замкнутой кривой , он называется циркуляцией поля по кривой и обозначается так:

Приняты и другие обозначения циркуляции:

15. Лекционное занятие. ВЫЧИСЛЕНИЕ ЛИНЕЙНОГО ИНТЕГРАЛА

Правило вычисления линейных интегралов в следующих двух случаях.

1). Для вычисления интеграла по линии , заданной уравнениями , следует:

а) записать интеграл в координатной форме

б) заменить в функциях соответственно на ,

в) заменить соответственно на ,

г) найти интервал изменения параметра и вычислить получившийся определенный интеграл по этому интервалу.

2). Для вычисления интеграла по плоской линии с уравнением следует:

а) записать интеграл в координатной форме ,

б) заменить в функциях на ,

г) вычислить получившийся определенный интеграл по отрезку .

3). В случае центрального поля следует учесть, что ; дифференцируя это равенство, получим и

т.е. линейный интеграл поля сведен к определенному интегралу.

Пример 1. Вычислить работу силы по прямолинейному перемещению из точки в точку .

Решение. Работа силы вычисляется по формуле

Для вычисления этого интеграла составим уравнение прямой :

Найдем значение параметра , соответствующее точке . Для этого подставим абсциссу точки в формулу . Получим . Аналогично найдем . Заменяя в интеграле их выражениями, получим

Пример 2. Найти циркуляцию поля вдоль линии , где ─ дуга параболы , ─ ломаная (рис. 1).

Решение. Циркуляцию поля вычислим по формуле

На отрезке имеем . Поэтому

На дуге имеем . Поэтому

Пример 3. Вычислить циркуляцию поля по окружности радиусом с центром в начале координат, ориентированной против часовой стрелки.

Решение. Циркуляция поля вычисляется по формуле

Для вычисления этого интеграла запишем параметрические уравнения окружности : .

Первый слайд презентации: Лекция 3 1. Линейный интеграл в векторном поле, его свойства. Работа силового поля. Циркуляция векторного поля, ее гидродинамический смысл и вычисление. Формула Стокса. Ротор векторного поля, его физический смысл. Плотность циркуляции. Безвихревое поле, потенциальное поле. Оператор Гамильтона, его свойства. Оператор Лапласа

Слайд 2: 1. Линейный интеграл в векторном поле. Циркуляция векторного поля

Пусть в 3-х мерном пространстве задано векторное поле, где P, Q, R интегрируемы вместе со своими производными. Пусть в пространстве задана гладкая ориентированная кривая AB. § 1. Линейный интеграл в векторном поле. Циркуляция векторного поля. 2

Слайд 3

3 В силу гладкости в каждой точке AB существует единственный вектор касательной, который может быть записан следующим образом:

Слайд 4

- углы которые составляет вектор с осями координат. Считаем, что дуга AB задана параметрически: AB : 4

Слайд 5

Тогда для координат единичного вектора касательной имеем: где соответствуют ориентации вектора совпадающего с ориентацией дуги AB, и не совпадающей с ориентацией дуги соответственно. 5

Слайд 6

Длина элемента дуги может быть найдена по формуле Рассмотрим в каждой точке дуги AB скалярное произведение Скалярное произведение представляет собой непрерывную по координатам x, y, z функцию. Из непрерывности скалярного произведения следует что существует: 6

Слайд 7

Этот интеграл называется линейным интегралом в векторном поле. Смысл интеграла: Пусть по дуге AB от действия вектора силы движется материальная точка единичной массы. Скалярное произведение есть проекция вектора на единичный вектор касательной. Если проекция получим элементарную работу, совершенную силой на перемещении dl в направлении вектора. 7

Слайд 8

Чтобы найти полную работу, необходимо проинтегрировать по всей длине дуги AB : - полная работа. Смысл линейного интеграла - работа, совершенная эти полем. Определение. (циркуляции векторного поля). Если существует в векторном поле линейный интеграл по ориентированному замкнутому контуру вида: 8

Слайд 9

то значение этого интеграла называется циркуляцией векторного поля и обозначается буквой Ц. Таким образом, циркуляция векторного поля есть работа векторного поля при движении по замкнутому контуру. 9

Слайд 10: 2. Теорема Стокса

Если в 3-х мерном пространстве функции P ( x, y, z ), Q ( x, y, z ), R ( x, y, z ), таковы, что: 1) Непрерывны вместе со своими производными 2) В пространстве задан гладкий, ориентированный, замкнутый, ограниченный контур 10

Слайд 11

3) Задана гладкая ориентированная поверхность S, натянутая на контур такая что, нормаль к поверхности и обход контура совмещены по правилу Буравчика. Тогда 11

Слайд 12

Формула, связывающая криволинейный интеграл по замкнутому контуру натянутая на поверхность S называется формулой Стокса. В частном случае, если поле плоское, R = 0, z = const, формула Стокса переходит в формулу Грина. 12

Слайд 13: 3. Ротор векторного поля. Векторная запись теоремы Стокса

Пусть имеется векторное поле вида: где P, Q, R непрерывны со своими производными. Рассмотрим в векторном поле замкнутый, гладкий, ориентированный контур ℓ, который является краем гладкой ориентируемой поверхности S. Нормаль к поверхности S и обход контура связаны по правилу Буравчика. 13

Слайд 14

Найдем работу, которую совершает векторное поле при движении по замкнутому контуру ℓ. Так как на контур ℓ натянута ориентируемая поверхность S, то 14

Слайд 15

Учитывая связь между поверхностными интегралами 2-го и 1-го рода имеем: Выражение, стоящее под знаком поверхностного интеграла 1-го рода можно записать как скалярное произведение: 15

Слайд 16

и единичного вектора нормали к поверхности Таким образом, работа по замкнутому контуру может быть записана: 16

Слайд 17

Вектор характеризует вращательную способность поля. Если он равен 0, то поле не совершает работу при движении по замкнутому контуру. Вектор называется ротором векторного поля (вихрем векторного поля) и обозначается: 17

Слайд 18: Векторная запись теоремы Стокса

Теорема Стокса связывает: Слева в формуле стоит циркуляция векторного поля по замкнутому контуру ℓ. 18

Слайд 19

Это векторная запись теоремы Стокса. Смысл: Циркуляция векторного поля равна потоку ротора этого векторного поля через поверхность S, натянутую на контур ℓ. 19

Слайд 20: 4. Плотность циркуляции, связь её с ротором

Пусть в векторном поле В произвольной точке пространства M задан вектор. Найдем циркуляцию векторного поля по замкнутому контуру ℓ, описываемому около точки M и лежащему в плоскости, перпендикулярной вектору. 20

Слайд 21

Если циркуляцию разделим на площадь контура ℓ, то получим число, характеризующее среднюю плотность циркуляции в контуре ℓ. 21

Слайд 22

Определение. (плотности циркуляции) Плотностью циркуляции в точке М по направлению вектора называется число, обозначаемое и вычисляемое по формуле: Когда контур ℓ стягивается в точку M. Можно показать, что плотность циркуляции в точке M по направлению вектора равна проекции ротора векторного поля на направление. 22

Слайд 23

§ 5. Вычисление циркуляции. Ее можно вычислить 2 способами: По определению, путем сведения к криволинейному интегралу 2-го рода. 2) С помощью теоремы Стокса. Пример: На практике.

Слайд 24

Определение. Векторное поле называется потенциальным, в некоторой односвязанной области V, если существует такая функция , что. Замечание. Функцию  называют потенциалом векторного поля. § 6. Потенциальное поле. Виды векторных полей.

Слайд 25

Пример: На практике.

Слайд 26

Теорема. (необходимое и достаточное условие потенциальности). Для того, чтобы векторное поле было потенциальным в некоторой односвязанной области V, необходимо и достаточно, чтобы циркуляция этого векторного поля по любому замкнутому контуру, лежащему в области V была равна нулю. Доказательство. Самостоятельно.

Слайд 27

Замечание. Потенциал векторного поля определен с точностью до константы. Если  - потенциал векторного поля, то есть = grad, то  + с – так же потенциал векторного поля. 0 grad (  + с ) = grad + grad с =. Для отыскания потенциала поля берут и фиксируют определенную точку в поле, в которой потенциал известен (бесконечно удаленную точку, в которой  = 0) и применяют формулу:

Слайд 28

Точка M 0 - фиксированная точка, в которой потенциал известен. Точка M - точка, в которой потенциал неизвестен. P,Q,R - координаты векторного поля, для которого находим потенциалы. - произвольная дуга, соединяющая две точки M 0 и M. Дуга берется произвольной в силу того, что интеграл 2-го рода не зависит от способа движения от точки M 0 к точке M, а зависит только от расположения этих точек в случае потенциального поля.

Слайд 29

§ 7. Безвихревые поля. Определение: Векторное поле называется безвихревым в односвязанной области V, если ротор этого векторного поля равен 0. rot = 0. Теорема. (необходимое и достаточное условие безвихревого поля): Для того, чтобы векторное поле было безвихревым необходимо и достаточно, чтобы оно было потенциальным в каждой точке некоторой области V.

Слайд 30

Доказательство Необходимость: Пусть векторное поле - безвихревое, то есть. Циркуляция векторного поля, по произвольному замкнутому контуру вычисляется по формуле, которая с учетом теоремы Стокса дает интеграл по поверхности ( по произвольному замкнутому контуру). В силу предыдущей теоремы это означает что - потенциальное поле. 30

Слайд 31

Достаточность : - потенциальное поле поле – безвихревое. § 8. Соленоидальные поля. Определение: Векторное поле называется соленоидальным в односвязанной области V, если: Теорема. (о соленоидальности векторного поля ). Для того, чтобы векторное поле было соленоидальным в односвязанной области V необходимо и достаточно, чтобы поток векторного поля через произвольную замкнутую поверхность, лежащую в области V, был равен нулю. 31

Слайд 32

32 Необходимость: Пусть - соленоидальное поле . Рассмотрим в области V произвольную замкнутую поверхность V, ориентированную внешней нормалью Достаточность: Предположим что поток через поверхность = 0.

Слайд 33

Свойства соленоидальных полей Пусть дано векторное поле. Считаем, что в поле построены векторные линии. Возьмем в поле замкнутый контур и через него проведем множество векторных линий. Это множество линий образует векторную трубку. 33

Слайд 34

34 Теорема. ( о постоянстве потока соленоидального поля). Поток соленоидального поля через любое сечение векторной трубки является постоянной величиной. Доказательство. Рассмотрим векторную трубку в векторном поле и возьмем пространство, заключенное в трубке, ограниченное сечениями S 1 и S 2. Объем векторной трубки, заключенный между сечениями S 1 и S 2 – замкнутый.

Слайд 35: Поверхность, ограничивающая объем состоит и з 3-х поверхностей, и, которые имеют единичные нормали. направленные как указано на рисунке. Поток векторного поля через поверхность S : S = S 1 + S 2 + S б можно вычислить по теореме Остроградского: Векторное поле соленоидально Откуда следует, что

Слайд 36

В силу определения векторной трубки , а следовательно, интеграл = 0. При вычислении потока через поверхность смотрят за направлением нормали к этой поверхности. При вычислении потока через считаем, что нормаль направлена в сторону потока. При вычислении потока берем нормаль, направленную в сторону потока. 36

Слайд 37

Заменим поток в направлении на поток в направлении имеем: Поток в трубке постоянен по сечению в случае соленоидального поля. 37

Слайд 38

38 § 9. Операции 1 и 2 порядка над скалярными и векторными полями. Пусть есть скалярное поле и векторное поле. Каждому скалярному полю с помощью градиента можно поставить векторное поле градиента. Любому дифференциальному векторному полю с помощью div можно поставить скалярное поле. Любому векторному полю с помощью можно поставить векторное поле. - операции 1-го порядка. Они показывают, что операции связаны между собой.

Слайд 39

39 Операции 1-го порядка порождают 5 операций 2-го порядка. 1. Дивергенция берется 2. от векторного поля. 3. 4. 5. Две из операций 2-го порядка равны 0.

Слайд 40

40 Раскрытие всех операций производится слева направо. Все они приводятся к вычислению частных производных 2-го порядка. Это первая из операций 2-го порядка, которая = 0.

Слайд 41

41 Рассмотрим: Это вторая операция 2-го порядка, которая равно нулю.

Слайд 42

42 Операцию 2-го порядка называют оператор Лапласа и обозначают: ∆ - оператор Лапласа (Лапласиан) Сравнивая обведённые выражения можем записать:

Слайд 43

43 Для электростатического поля, в случае стационарного поля. div =  - объемная плотность заряда = grad  Электростатическое поле является потенциальным - уравнение Лапласа. В случае электростатического поля функция потенциала подчиняется уравнению, где  - неизвестная заранее функция.

Слайд 44

Слайд 45

45 Операции 1-го порядка записываются в виде: - скалярное произведение - векторное произведение Запись операций 2-го порядка с помощью оператора Набла: 1) - оператор Лапласа равен оператору Набла в квадрате.

Читайте также: