Квантование по времени реферат
Обновлено: 03.07.2024
В настоящее время информация стала фактором, определяющим эффективность любой сферы деятельности. Увеличились информационные потоки и повысились требования к скорости передачи данных, одним из факторов повышения скорости передачи данных служит метод дискретизации сигналов по времени, т.е. при передачи сигнала, можно передавать не весь сигнал, а только его отчеты, и восстанавливать сигнал по отчетам. В этом случае передаются только импульсы (щелчки), а на приемнике, по этим щелчкам восстанавливается сигнал
В работе реализуется алгоритм квантования сигналов по времени.
1. Классификация видов модуляции
Таким образом, преобразование сигналов при передаче состоит в воздействии на переносчик, изменяющем тот или иной его параметр. Это воздействие называется модуляцией.
Различные виды модуляции характеризуются различными видами переносчиков, а так же рядом параметров, подвергаемых изменению.
По виду переносчиков различают:
модуляцию синусоидальных (гармонических) сигналов;
модуляцию импульсных сигналов.
По изменяемым параметрам различают:
кодовую модуляцию и др.
2. Модуляция импульсных переносчиков
В новейших системах передачи информации, в особенности в многоканальных системах с временным уплотнением (разделением) каналов, переносчиком является последовательность прямоугольных импульсов. У такого переносчика можно изменять следующие параметры: амплитуду импульсов, их ширину, частоту следования, позицию или фазу и коды, образуемые ими. Соответственно различают следующие модуляции:
амплитудно-импульсная модуляция АИМ;
широтно-импульсная модуляция ШИМ;
время-импульсная модуляция ВИМ;
позиционно-импульсная модуляция (фазо-импульсная) ПИМ (ФИМ);
частотно-импульсная модуляция ЧИМ;
кодо-импульсная модуляция КИМ.
дискретизации сигналов по времени;
дискретизации сигналов по уровню;
Дискретизация по времени заключается в замене непрерывного по времени сигнала X(t) дискретным сигналом, значения которого для дискретных моментов времени t совпадают соответственно с мгновенными значениями непрерывного сигнала. Такая операция называется также квантованием сигнала по времени.
Дискретизация по уровню (квантование по уровню) заключается в замене непрерывного множества значений сигнала X(t) множеством дискретных значений. При этом шкала возможных значений сигнала разбивается на определенное количество интервалов и непрерывное значение сигнала заменяется ближайшим дискретным. Полученные дискретные значения затем кодируются (обычно двоичным кодом).
При КИМ весьма важным является правильный выбор способа квантования сигнала по времени и уровню. В связи с этим рассмотрим некоторые вопросы теории квантования непрерывных функций по времени и уровню.
3. Квантование сигналов по времени
3.1 Определение дискретизации сигналов по времени
При квантовании по времени непрерывная по аргументу функция x(t) преобразуется в функцию дискретного аргумента. Такое преобразование может быть выполнено путем взятия отсчетов функции x(t) в определенные дискретные моменты времени . В результате функция x(t) заменяется совокупностью мгновенных значений x(ti) [i=0,1,2,…,n].
Временной интервал между двумя соседними фиксированными моментами времени, в которых задается дискретная функция, называется интервалом временного квантования. Величина, обратная интервалу временного квантования называется частотой квантования.
Частота квантования должна выбираться таким образом, чтобы по отсчетным значениям x(ti) можно было бы с заданной точностью получить исходную функцию.
3.2 Выбор шага квантования по времени
Известно несколько критериев выбора частоты квантования по времени. К таким критериям относится, в частности, частотный критерий В.А. Котельникова. Данный критерий, который получил название теоремы В.А. Котельникова, основывается на следующей модели сигналов:
сигнал представляет собой стационарный случайный процесс;
спектр сигнала сплошной и ограничен некоторой частотой, за пределами которой он тождественно равен нулю.
Теорема В.А. Котельникова: если непрерывная функция x(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывная и имеет конечное число экстремумов) и ее спектр ограничен некоторой частотой fc, то она полностью определяется отсчетами, находящимися на расстоянии друг от друга.
Для доказательства теоремы рассмотрим выражения прямого и обратного преобразования Фурье непрерывной функции x(t).
В рассматриваемом частном случае функции с ограниченным спектром можно записать
Дополним функцию до периодической с периодом, равным 2fc (рисунок 1) и разложим ее в ряд Фурье
Рисунок 1 - функция с периодом, равным 2fc.
Сравнивая выражения (3) и (5) замечаем, что они совпадают с точностью до постоянного множителя , если принять .
Подставив найденное выражение для в (4), получим
После подставки (6) в (3), замены знака при k (т.к. суммирование производится по всем положительным и отрицательным значениям k) и перестановки операций суммирования и интегрирования получим
После подстановки (8) в (7) окончательно получим
Полученное выражение представляет аналитически теорему Котельникова.
Из (9) видно, что непрерывная функция X(t) (рисунок 2, а), обладающая ограниченным спектром, может быть представлена разложением в ряд, каждый член которого выражается одинаковой функцией вида sin(x)/x (функция отсчета), но с различными коэффициентами (рисунок 2, б).
Рисунок 2, а - Функция отсчета
Рисунок 2, б - Функция отсчета, но с различными коэффициентами
Ряд (9) представляет собой разложение случайного процесса с координатными функциями (детерминированными функциями времени) и весовыми коэффициентами , являющимися случайными величинами, равными мгновенным значениям сигнала в точках .
Функция отсчетов в момент времени достигает максимума и равна единице. В моменты времени , где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.
Сумма (9) в каждый k-ый момент времени определяется только одним k-ым слагаемым, т.к. все остальные слагаемые в этот момент времени обращается в нуль. Внутри промежутка восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).
3.3 Воспроизведение непрерывного сигнала
Известно, что функция вида представляет собой реакцию идеального фильтра нижних частот с граничной частотой на дельта-функцию. Следовательно, если в приемном устройстве поместить такой фильтр и пропустить через него квантованный сигнал, представляющий собой последовательность с частотой весьма кратковременных импульсов, амплитуды которых пропорциональны отсчетам исходной непрерывной функции, то, суммируя выходные сигналы фильтра, можно воспроизвести с достаточно высокой степенью точности исходный непрерывный сигнал.
Однако нас интересует случай, когда сигнал x(t) ограничен во времени (Tc). В этом случае сумма (9) будет конечной
Усечение бесконечной суммы, т.е. ограничение ее теми значениями Xk, которые оказываются в пределах Tc, уменьшает точность представления сигнала x(t).
Это первый фактор, определяющий точность представления.
Кроме того, сигнал конечной длительности имеет бесконечный спектр гармонических составляющих. Поэтому ограничение спектра сигнала некоторой частотой является вторым фактором, снижающим точность представления непрерывного сигнала x(t) дискретными отсчетами.
Средний квадрат относительной погрешности в этом случае определяется выражением
где Е – полная энергия неограниченного спектра сигнала;
Чтобы погрешность формулы (10) была мала, должно выполняться условие
Дополнительная погрешность вносится при восстановлении сигнала x(t) за счет не идеальности фильтра нижних частот, т.к. идеальный фильтр НЧ физически нереализуем (предполагает наличие отклика на -функцию при t maxi) then
function fmod(x,y: Real): Real;
Result := x - (x / y) * y;
procedure TForm1.sdf2Click(Sender: TObject);
procedure TForm1.sf1Click(Sender: TObject);
procedure TForm1.dsf1Click(Sender: TObject);
procedure TForm1.sd1Click(Sender: TObject);
procedure TForm1.sdf1Click(Sender: TObject);
Application.MessageBox('Тема: Квантование сигналов по времени','О программе',0);
procedure TForm1.sdf3Click(Sender: TObject);
Application.MessageBox('Выполнила студентка 3 курса группы 03-КТ-11, А. Л.','Об авторе',0);
procedure TForm1.FormCreate(Sender: TObject);
Заключение
В данной работе был реализован алгоритм квантования сигала по времени. Из проделанной работы можно сделать вывод, что при реальной передачи сигналов восстановленный сигнал, при большом (редком) шаге квантованья, сильно отличается от исходного. Следовательно, для того, чтобы сигнал передать как можно более точно необходимо часто передавать отчеты. Т.е чем меньше шаг квантования, тем больше соответствие восстановленного сигнала с исходным
Разработанная программа реализует восстановление исходного сигнала по отчетам, а также предоставляет гибкий характер работы пользователя с программным приложением по изменению параметров.
Разработанное приложение может быть незаменимой частью более сложных программных пакетов для передачи данных.
А.В.Власенко, В.И.Ключко - Теория информации и сигналов. Учебное пособие / Краснодар: Изд-во КубГТУ, 2003.- 97 с.
Теория передачи сигналов: Учебник для вузов / А.Г.Зюко, Д.Д.Кловский,
Цифровая обработка сигналов: Учебник для вузов / А.Б. Сергиенко – СПб.: Питер, 2003. – 604 с.: ил.
В настоящее время информация стала фактором, определяющим эффективность любой сферы деятельности. Увеличились информационные потоки и повысились требования к скорости передачи данных, одним из факторов повышения скорости передачи данных служит метод дискретизации сигналов по времени, т.е. при передачи сигнала, можно передавать не весь сигнал, а только его отчеты, и восстанавливать сигнал по отчетам. В этом случае передаются только импульсы (щелчки), а на приемнике, по этим щелчкам восстанавливается сигнал
В работе реализуется алгоритм квантования сигналов по времени.
Таким образом, преобразование сигналов при передаче состоит в воздействии на переносчик, изменяющем тот или иной его параметр. Это воздействие называется модуляцией.
Различные виды модуляции характеризуются различными видами переносчиков, а так же рядом параметров, подвергаемых изменению.
По виду переносчиков различают:
модуляцию синусоидальных (гармонических) сигналов;
модуляцию импульсных сигналов.
По изменяемым параметрам различают:
кодовую модуляцию и др.
В новейших системах передачи информации, в особенности в многоканальных системах с временным уплотнением (разделением) каналов, переносчиком является последовательность прямоугольных импульсов. У такого переносчика можно изменять следующие параметры: амплитуду импульсов, их ширину, частоту следования, позицию или фазу и коды, образуемые ими. Соответственно различают следующие модуляции:
амплитудно-импульсная модуляция АИМ;
широтно-импульсная модуляция ШИМ;
время-импульсная модуляция ВИМ;
позиционно-импульсная модуляция (фазо-импульсная) ПИМ (ФИМ);
частотно-импульсная модуляция ЧИМ;
кодо-импульсная модуляция КИМ.
дискретизации сигналов по времени;
дискретизации сигналов по уровню;
Дискретизация по времени заключается в замене непрерывного по времени сигнала X(t) дискретным сигналом, значения которого для дискретных моментов времени t совпадают соответственно с мгновенными значениями непрерывного сигнала. Такая операция называется также квантованием сигнала по времени.
Дискретизация по уровню (квантование по уровню) заключается в замене непрерывного множества значений сигнала X(t) множеством дискретных значений. При этом шкала возможных значений сигнала разбивается на определенное количество интервалов и непрерывное значение сигнала заменяется ближайшим дискретным. Полученные дискретные значения затем кодируются (обычно двоичным кодом).
При КИМ весьма важным является правильный выбор способа квантования сигнала по времени и уровню. В связи с этим рассмотрим некоторые вопросы теории квантования непрерывных функций по времени и уровню.
При квантовании по времени непрерывная по аргументу функция x(t) преобразуется в функцию дискретного аргумента. Такое преобразование может быть выполнено путем взятия отсчетов функции x(t) в определенные дискретные моменты времени . В результате функция x(t) заменяется совокупностью мгновенных значений x(ti) [i=0,1,2,…,n].
Временной интервал между двумя соседними фиксированными моментами времени, в которых задается дискретная функция, называется интервалом временного квантования. Величина, обратная интервалу временного квантованияназывается частотой квантования.
Частота квантования должна выбираться таким образом, чтобы по отсчетным значениям x(ti) можно было бы с заданной точностью получить исходную функцию.
Известно несколько критериев выбора частоты квантования по времени. К таким критериям относится, в частности, частотный критерий В.А. Котельникова. Данный критерий, который получил название теоремы В.А. Котельникова, основывается на следующей модели сигналов:
сигнал представляет собой стационарный случайный процесс;
спектр сигнала сплошной и ограничен некоторой частотой, за пределами которой он тождественно равен нулю.

Теорема В.А. Котельникова: если непрерывная функция x(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывная и имеет конечное число экстремумов) и ее спектр ограничен некоторой частотой fc, то она полностью определяется отсчетами, находящимися на расстоянии друг от друга.
Для доказательства теоремы рассмотрим выражения прямого и обратного преобразования Фурье непрерывной функции x(t).

(1)

. (2)
В рассматриваемом частном случае функции с ограниченным спектром можно записать

. (3)
Дополним функцию до периодической с периодом, равным 2fc (рисунок 1) и разложим ее в ряд Фурье

Рисунок 1 - функция с периодом, равным 2fc.

, (4)

. (5)
Сравнивая выражения (3) и (5) замечаем, что они совпадают с точностью до постоянного множителя , если принять .

.

Подставив найденное выражение для в (4), получим

. (6)
После подставки (6) в (3), замены знака при k (т.к. суммирование производится по всем положительным и отрицательным значениям k) и перестановки операций суммирования и интегрирования получим

. (7)

(8)

т.к. .
После подстановки (8) в (7) окончательно получим

. (9)
Полученное выражение представляет аналитически теорему Котельникова.

Из (9) видно, что непрерывная функция X(t) (рисунок 2, а), обладающая ограниченным спектром, может быть представлена разложением в ряд, каждый член которого выражается одинаковой функцией вида sin(x)/x (функция отсчета), но с различными коэффициентами (рисунок 2, б).

Рисунок 2, а - Функция отсчета


Рисунок 2, б - Функция отсчета, но с различными коэффициентами
Ряд (9) представляет собой разложение случайного процесса с координатными функциями (детерминированными функциями времени) и весовыми коэффициентами , являющимися случайными величинами, равными мгновенным значениям сигнала в точках .
Функция отсчетов в момент времени достигает максимума и равна единице. В моменты времени , где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.

Сумма (9) в каждый k-ый момент времени определяется только одним k‑ым слагаемым, т.к. все остальные слагаемые в этот момент времени обращается в нуль. Внутри промежутка восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).
Известно, что функция вида представляет собой реакцию идеального фильтра нижних частот с граничной частотой на дельта-функцию. Следовательно, если в приемном устройстве поместить такой фильтр и пропустить через него квантованный сигнал, представляющий собой последовательность с частотой весьма кратковременных импульсов, амплитуды которых пропорциональны отсчетам исходной непрерывной функции, то, суммируя выходные сигналы фильтра, можно воспроизвести с достаточно высокой степенью точности исходный непрерывный сигнал.
Однако нас интересует случай, когда сигнал x(t) ограничен во времени (Tc). В этом случае сумма (9) будет конечной

, (10)

где .
Усечение бесконечной суммы, т.е. ограничение ее теми значениями Xk, которые оказываются в пределах Tc, уменьшает точность представления сигнала x(t).
Это первый фактор, определяющий точность представления.

Кроме того, сигнал конечной длительности имеет бесконечный спектр гармонических составляющих. Поэтому ограничение спектра сигнала некоторой частотой является вторым фактором, снижающим точность представления непрерывного сигнала x(t) дискретными отсчетами.
Средний квадрат относительной погрешности в этом случае определяется выражением

,
где Е – полная энергия неограниченного спектра сигнала;
Чтобы погрешность формулы (10) была мала, должно выполняться условие

. (11)

Дополнительная погрешность вносится при восстановлении сигнала x(t) за счет не идеальности фильтра нижних частот, т.к. идеальный фильтр НЧ физически нереализуем (предполагает наличие отклика на -функцию при t maxi) then
В настоящее время информация стала фактором, определяющим эффективность любой сферы деятельности. Увеличились информационные потоки и повысились требования к скорости передачи данных, одним из факторов повышения скорости передачи данных служит метод дискретизации сигналов по времени, т.е. при передачи сигнала, можно передавать не весь сигнал, а только его отчеты, и восстанавливать сигнал по отчетам. В этом случае передаются только импульсы (щелчки), а на приемнике, по этим щелчкам восстанавливается сигнал
В работе реализуется алгоритм квантования сигналов по времени.
Таким образом, преобразование сигналов при передаче состоит в воздействии на переносчик, изменяющем тот или иной его параметр. Это воздействие называется модуляцией.
Различные виды модуляции характеризуются различными видами переносчиков, а так же рядом параметров, подвергаемых изменению.
По виду переносчиков различают:
модуляцию синусоидальных (гармонических) сигналов;
модуляцию импульсных сигналов.
По изменяемым параметрам различают:
кодовую модуляцию и др.
В новейших системах передачи информации, в особенности в многоканальных системах с временным уплотнением (разделением) каналов, переносчиком является последовательность прямоугольных импульсов. У такого переносчика можно изменять следующие параметры: амплитуду импульсов, их ширину, частоту следования, позицию или фазу и коды, образуемые ими. Соответственно различают следующие модуляции:
амплитудно-импульсная модуляция АИМ;
широтно-импульсная модуляция ШИМ;
время-импульсная модуляция ВИМ;
позиционно-импульсная модуляция (фазо-импульсная) ПИМ (ФИМ);
частотно-импульсная модуляция ЧИМ;
кодо-импульсная модуляция КИМ.
дискретизации сигналов по времени;
дискретизации сигналов по уровню;
Дискретизация по времени заключается в замене непрерывного по времени сигнала X(t) дискретным сигналом, значения которого для дискретных моментов времени t совпадают соответственно с мгновенными значениями непрерывного сигнала. Такая операция называется также квантованием сигнала по времени.
Дискретизация по уровню (квантование по уровню) заключается в замене непрерывного множества значений сигнала X(t) множеством дискретных значений. При этом шкала возможных значений сигнала разбивается на определенное количество интервалов и непрерывное значение сигнала заменяется ближайшим дискретным. Полученные дискретные значения затем кодируются (обычно двоичным кодом).
При КИМ весьма важным является правильный выбор способа квантования сигнала по времени и уровню. В связи с этим рассмотрим некоторые вопросы теории квантования непрерывных функций по времени и уровню.
При квантовании по времени непрерывная по аргументу функция x(t) преобразуется в функцию дискретного аргумента. Такое преобразование может быть выполнено путем взятия отсчетов функции x(t) в определенные дискретные моменты времени . В результате функция x(t) заменяется совокупностью мгновенных значений x(ti) [i=0,1,2,…,n].
Временной интервал между двумя соседними фиксированными моментами времени, в которых задается дискретная функция, называется интервалом временного квантования. Величина, обратная интервалу временного квантованияназывается частотой квантования.
Частота квантования должна выбираться таким образом, чтобы по отсчетным значениям x(ti) можно было бы с заданной точностью получить исходную функцию.
Известно несколько критериев выбора частоты квантования по времени. К таким критериям относится, в частности, частотный критерий В.А. Котельникова. Данный критерий, который получил название теоремы В.А. Котельникова, основывается на следующей модели сигналов:
сигнал представляет собой стационарный случайный процесс;
спектр сигнала сплошной и ограничен некоторой частотой, за пределами которой он тождественно равен нулю.
Теорема В.А. Котельникова: если непрерывная функция x(t) удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывная и имеет конечное число экстремумов) и ее спектр ограничен некоторой частотой fc, то она полностью определяется отсчетами, находящимися на расстоянии друг от друга.
Для доказательства теоремы рассмотрим выражения прямого и обратного преобразования Фурье непрерывной функции x(t).
В рассматриваемом частном случае функции с ограниченным спектром можно записать
Дополним функцию до периодической с периодом, равным 2fc (рисунок 1) и разложим ее в ряд Фурье
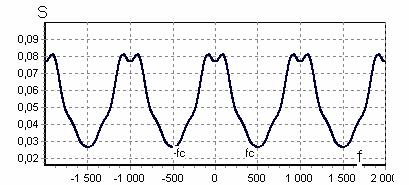
Рисунок 1 - функция с периодом, равным 2fc.
Сравнивая выражения (3) и (5) замечаем, что они совпадают с точностью до постоянного множителя , если принять .
Подставив найденное выражение для в (4), получим
После подставки (6) в (3), замены знака при k (т.к. суммирование производится по всем положительным и отрицательным значениям k) и перестановки операций суммирования и интегрирования получим
После подстановки (8) в (7) окончательно получим
Полученное выражение представляет аналитически теорему Котельникова.
Из (9) видно, что непрерывная функция X(t) (рисунок 2, а), обладающая ограниченным спектром, может быть представлена разложением в ряд, каждый член которого выражается одинаковой функцией вида sin(x)/x (функция отсчета), но с различными коэффициентами (рисунок 2, б).
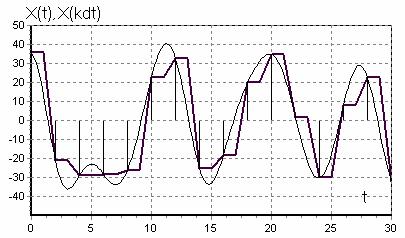
Рисунок 2, а - Функция отсчета
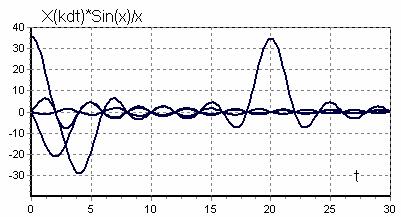
Рисунок 2, б - Функция отсчета, но с различными коэффициентами
Ряд (9) представляет собой разложение случайного процесса с координатными функциями (детерминированными функциями времени) и весовыми коэффициентами , являющимися случайными величинами, равными мгновенным значениям сигнала в точках .
Функция отсчетов в момент времени достигает максимума и равна единице. В моменты времени , где i=1,2,3… функция отсчетов убывает, обращаясь в нуль при t=∞.
Сумма (9) в каждый k-ый момент времени определяется только одним k-ым слагаемым, т.к. все остальные слагаемые в этот момент времени обращается в нуль. Внутри промежутка восстанавливаемая функция определяется всеми слагаемыми (рисунок 21, а - непрерывная плавная линия).
Известно, что функция вида представляет собой реакцию идеального фильтра нижних частот с граничной частотой на дельта-функцию. Следовательно, если в приемном устройстве поместить такой фильтр и пропустить через него квантованный сигнал, представляющий собой последовательность с частотой весьма кратковременных импульсов, амплитуды которых пропорциональны отсчетам исходной непрерывной функции, то, суммируя выходные сигналы фильтра, можно воспроизвести с достаточно высокой степенью точности исходный непрерывный сигнал.
Однако нас интересует случай, когда сигнал x(t) ограничен во времени (Tc). В этом случае сумма (9) будет конечной
Усечение бесконечной суммы, т.е. ограничение ее теми значениями Xk, которые оказываются в пределах Tc, уменьшает точность представления сигнала x(t).
Это первый фактор, определяющий точность представления.
Кроме того, сигнал конечной длительности имеет бесконечный спектр гармонических составляющих. Поэтому ограничение спектра сигнала некоторой частотой является вторым фактором, снижающим точность представления непрерывного сигнала x(t) дискретными отсчетами.
Средний квадрат относительной погрешности в этом случае определяется выражением
где Е – полная энергия неограниченного спектра сигнала;
Чтобы погрешность формулы (10) была мала, должно выполняться условие
Дополнительная погрешность вносится при восстановлении сигнала x(t) за счет не идеальности фильтра нижних частот, т.к. идеальный фильтр НЧ физически нереализуем (предполагает наличие отклика на -функцию при t 4. Руководство пользователя
На рисунке 3 показан внешний вид программы при запуске.
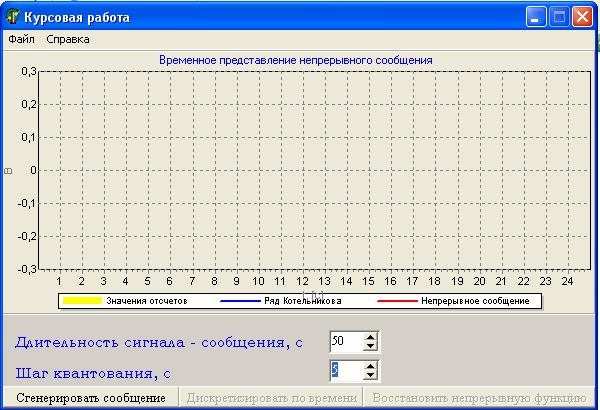
Рисунок 3. Внешний вид рабочего окна программы
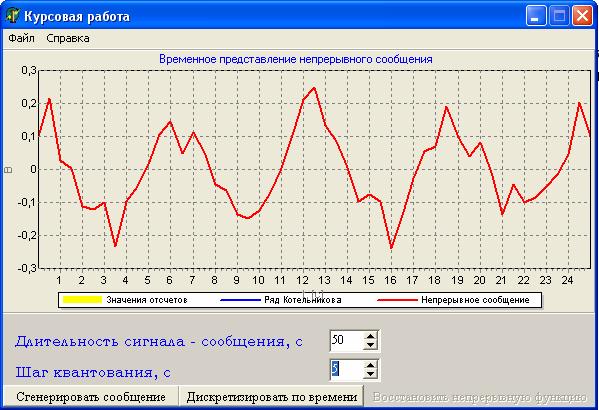
Рисунок 4 – Вывод на экран случайной функции
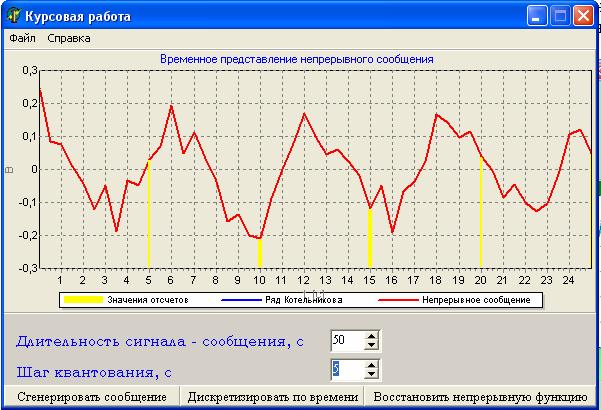
Рисунок 5 – Отображение отчетов, соответственно шагу квантования.
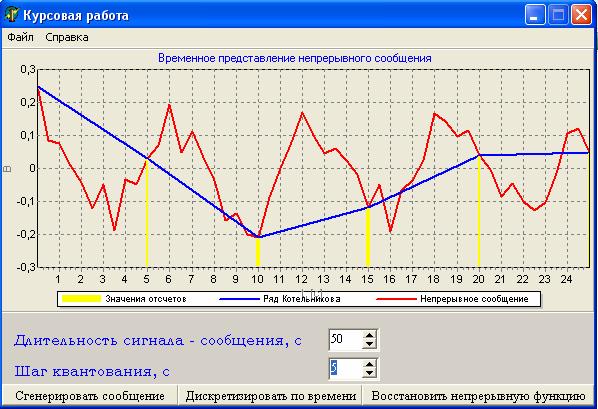
Рисунок 6 – Отображение восстановленного сигнала по отчетам.
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Подавляющее большинство технологических параметров являются аналоговыми, т.е. непрерывно изменяющимися во времени. Привлечение цифрового устройства — ЭВМ — к контролю и управлению технологическими процессами требует решения двух вопросов: в какие моменты времени измерять аналоговые параметры и как преобразовывать в конкретное число значение параметра, которое может быть совершенно произвольным (конечно, в заданных пределах). Ответы на эти вопросы связаны с двумя процессами: квантованием по времени и квантованием по уровню — заменой аналогового (непрерывного) сигнала дискретными (фиксированными, а значит, следующими друг за другом с разрывом) значениями.
Квантование по времени заключается в том, что из аналогового (непрерывного) сигнала выбираются отдельные его значения,
соответствующие моментам, когда измерительная аппаратура выполняет очередное измерение, т.е. преобразование этого сигнала в цифровой код. Моменты преобразования сигнала обозначены на рис. 5.20, а как t\, t2 и т.д. Кружками (см. рис. 5.20, а) показаны значения сигнала в эти моменты, которые являются произвольными. Чем реже будут следовать моменты преобразования сигнала, тем сильнее он может измениться за промежуток времени между двумя преобразованиями, следовательно, снижается точность его преобразования. Поэтому чем быстрее может изменяться входной сигнал, тем чаще должны выполняться его преобразования, т.е. больше должна быть частота квантования.
Квантование по уровню заключается в создании шкалы уровней квантования, заполняющей весь диапазон возможных значений непрерывного сигнала (рис. 5.20, б). Уровни квантования отстоят друг от друга на шаг квантования, который определяется точностью измерения сигнала используемой аппаратурой. При квантовании точные значения сигнала заменяются на ближайшие к ним значения шкалы квантования, т.е. округляются. Это хорошо видно на рис. 5.20, б, где для сравнения штриховой линией показан входной сигнал. Следовательно, для повышения точности преобразования следует уменьшать шаг квантования, повышая точность измерительной аппаратуры.

линией на рис. 5.20, б, таким, как он представлен полужирной линией на этом рисунке.
Читайте также:

